深度精度是每一個圖形程序員遲早都要面對的難題。關于這個主題已經寫了很多文章和論文，在不同的游戲、引擎和設備中可以找到各種不同的深度緩沖格式和設置。

由于它與透視投影交互的方式， GPU 硬件深度映射有點晦澀難懂，研究這些方程可能不會讓事情立即變得顯而易見。為了獲得它如何工作的直覺，畫一些圖片是很有幫助的。

這篇文章有三個主要部分。在第一部分中，我試圖為非線性深度映射提供一些動機。其次，我提供了一些圖表來幫助理解非線性深度映射在不同情況下是如何工作的，直觀且直觀。第三部分是 Paul Upchurch 和 Mathieu Desbrun （ 2012 ）關于浮點舍入誤差對深度精度影響的提高透視渲染的精度主要結果的討論和再現。

為什么是 1 / z

GPU 硬件深度緩沖區通常不會存儲對象在相機前面的距離的線性表示，這與您第一次遇到這種情況時天真的期望相反。相反，深度緩沖區存儲的值與世界空間深度的倒數成比例。我想簡要介紹一下這次大會。

在本文中，我使用d表示深度緩沖區中存儲的值（在[0 ， 1]中），并使用z表示世界空間深度，即沿視圖軸的距離，以世界單位（如米）表示。一般而言，它們之間的關系如下：

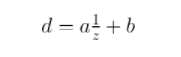
在此公式中，a和b是與近平面和遠平面設置相關的常數。換言之，d始終是1/z.從表面上看，您可以想象將d作為您喜歡的z的任何函數。那么，為什么會有這種特殊的選擇呢？有兩個主要原因。First,1/z自然適合透視投影的框架。這是保證保持直線的最普通的變換類，這使得硬件光柵化變得很方便，因為三角形的直邊在屏幕空間中保持筆直。可以生成的線性重映射1/z通過利用硬件已經執行的透視圖劃分：

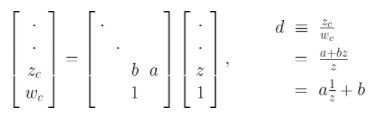
當然，這種方法的真正威力在于投影矩陣可以與其他矩陣相乘，從而允許您將多個變換階段組合在一個矩陣中。

第二個原因是1/z在屏幕空間中是線性的，如埃米爾·佩爾松所述。因此，在柵格化的同時，在三角形上插值d是很容易的，而像分層 Z 緩沖區、早期 Z 消隱和深度緩沖區壓縮這樣的事情都要容易得多。

繪制深度圖

方程是硬的；這里有一些照片！

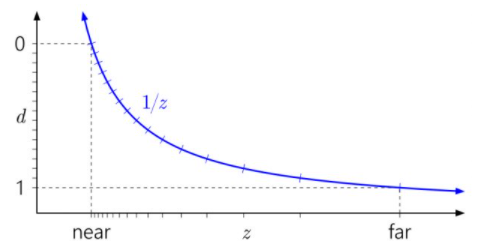
閱讀這些圖表的方法是從左到右，然后從下到下。從d開始，繪制在左軸上。因為d可以是1/z，您可以將 0 和 1 放置在此軸上任意位置。勾號表示不同的深度緩沖區值。為了便于說明，我正在模擬一個 4 位標準化整數深度緩沖區，因此有 16 個等距記號。

水平追蹤刻度線，直到它們擊中目標的位置1/z曲線，然后向下至底部軸。這就是世界空間深度范圍中不同值的位置。

圖 1 顯示了 D3D 和類似 API 中使用的“標準”深度映射。您可以立即看到1/z曲線會導致靠近近平面的值聚集在一起，而靠近遠平面的值分布得非常分散。

也很容易看出為什么近平面對深度精度有如此深遠的影響。拉近近飛機將使d射程向上飛向飛機的漸近線1/z曲線，導致更不平衡的值分布：

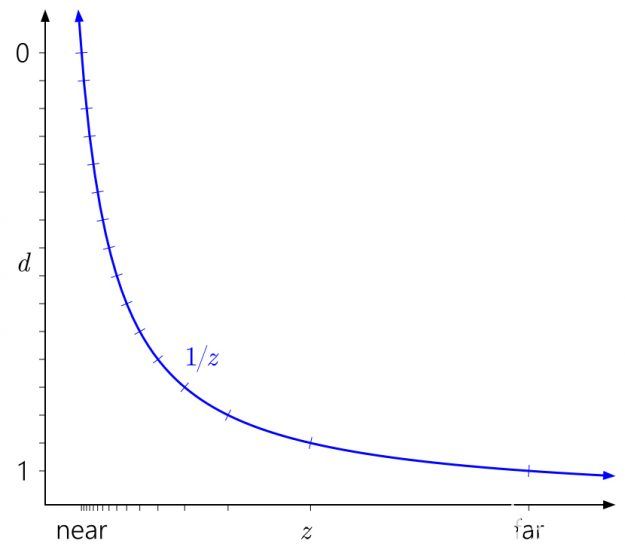
類似地，在這種情況下，很容易看出為什么將遠平面一直推到無窮遠沒有那么大的效果。這只是意味著將d范圍稍微向下擴展到

:

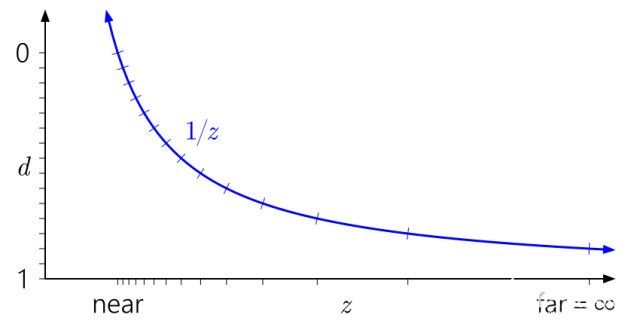
浮點深度呢？下圖添加了與具有三個指數位和三個尾數位的模擬浮點格式相對應的記號：

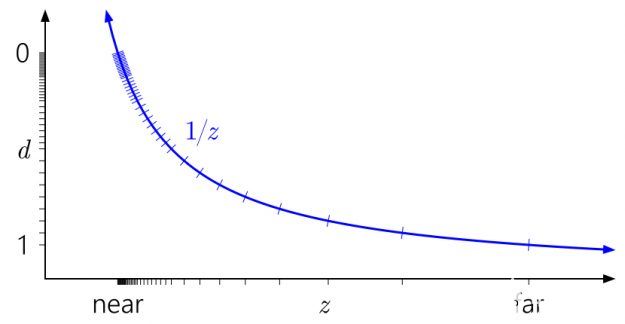
[0 , 1]中現在有 40 個不同的值——比以前的 16 個值多了一點，但它們中的大多數都無用地聚集在不需要更高精度的近平面上。

現在廣為人知的一個技巧是反轉深度范圍，將近平面映射到d=1，將遠平面映射到d=0：

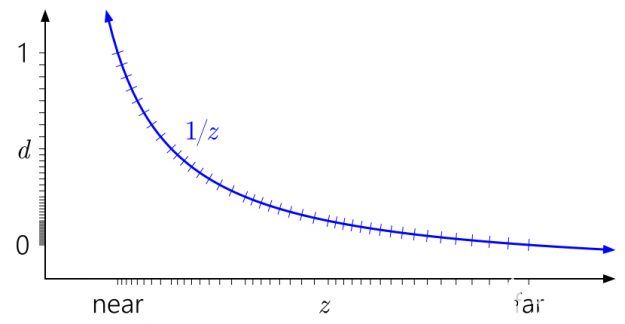
好多了！現在，浮點的準對數分布在某種程度上抵消了1/z非線性，使您在近平面的精度與整數深度緩沖區相似，并大大提高了其他地方的精度。當你向遠處移動時，精度只會慢慢降低。

反向 -Z 技巧可能已經被獨立地重新發明了好幾次，但至少可以追溯到 Eugene Lapidous 和 Guofang Jiao （不幸的是，沒有可用的開放訪問鏈接）撰寫的 SIGGRAPH ‘ 99 論文低成本圖形硬件的最佳深度緩沖。最近，馬特·佩蒂尼奧。和布拉諾·凱門以及埃米爾·佩爾松的創造廣闊的游戲世界 SIGGRAPH 2012 年講座在帖子中重新推廣了這一概念。

之前的所有圖表均假定[0 , 1]為投影后深度范圍，這是 D3D 約定。那 OpenGL 呢？

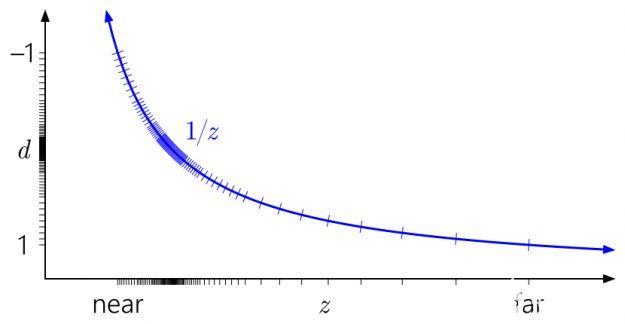
默認情況下， OpenGL 假定投影后深度范圍為[-1 , 1]。這對整數格式不起作用，但是用浮點，所有的精度都在中間被無用地卡住。（該值被映射到[0 ， 1]以便稍后存儲在深度緩沖區中，但這并沒有幫助，因為到[-1 ， 1]的初始映射已經破壞了該范圍最遠一半的所有精度。）根據對稱性，反轉 -Z 技巧在這里沒有任何作用。

幸運的是，在桌面 OpenGL 中，您可以通過廣泛支持的ARB_clip_control擴展（現在也是 OpenGL 4 . 5 中的核心glClipControl）來解決這個問題。不幸的是，在德國，你運氣不好。

舍入誤差的影響

The 1/z映射和浮點與整數深度緩沖區的選擇是精度故事的重要部分，但不是全部。即使您有足夠的深度精度來表示要渲染的場景，也很容易最終得到由頂點變換過程的算術錯誤控制的精度。

如前所述，厄普丘奇和德斯布倫對此進行了研究，并提出了兩項主要建議，以盡量減少舍入誤差：

使用一個無限遠的平面。

將投影矩陣與其他矩陣分開，并在頂點著色器中的單獨操作中應用它，而不是將其組合到視圖矩陣中。

Upchurch 和 Desbrun 通過分析技術提出了這些建議，其基礎是將舍入誤差視為每次算術運算中引入的小隨機擾動，并通過轉換過程將其跟蹤到一階。我決定使用直接模擬來檢查結果。

這是我的源代碼 – Python 3 . 4 和 NumPy 。它的工作原理是生成一系列隨機點，按深度排序，在近平面和遠平面之間線性或對數間隔。然后，它使用 32 位浮點精度將點通過視圖和投影矩陣以及透視分割，并可選地將最終結果量化為 24 位整數。

最后，它遍歷序列并計算兩個相鄰點（最初具有不同深度）由于映射到相同深度值而變得不可區分或實際交換順序的次數。換句話說，它測量深度比較錯誤發生的速率，這與不同場景下的 Z- 戰斗等問題相對應。

以下是近距離= 0 . 1 ，遠距離= 10K ，線性間隔深度為 10K 時獲得的結果。（我也嘗試了對數深度間距和其他近/遠比率，雖然詳細數字各不相同，但結果的總體趨勢是相同的。）

在表中，“不可區分”表示不可區分（兩個相鄰深度映射到相同的最終深度緩沖區值），“交換”表示兩個相鄰深度交換順序。

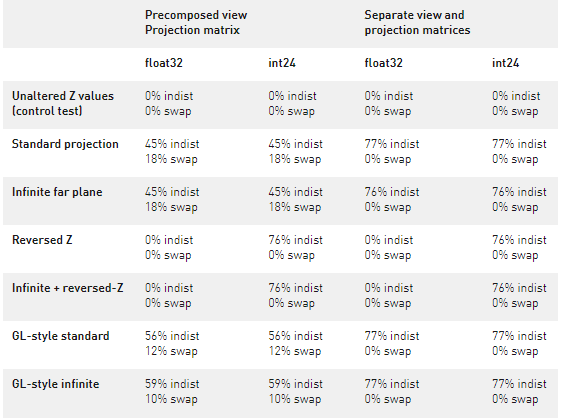
很抱歉沒有繪制這些，但是有太多的維度，使其易于繪制！不管怎樣，看看這些數字，一些普遍的結果是清楚的。

在大多數設置中，浮點深度緩沖區和整數深度緩沖區之間沒有區別。算術誤差淹沒了量化誤差。這在一定程度上是因為 float32 和 int24 在[0 . 5 , 1]中具有幾乎相同大小的 ulp （因為 float32 具有 23 位尾數），因此實際上在絕大多數深度范圍內幾乎沒有額外的量化誤差。

在許多情況下，分離視圖矩陣和投影矩陣（遵循 Upchurch 和 Desbrun 的建議）確實會帶來一些改進。雖然這并沒有降低總體錯誤率，但它似乎確實將互換變成了無法區分的東西，這是朝著正確方向邁出的一步。

一個無限遠的平面在錯誤率上的差別很小。 Upchurch 和 Desbrun 預測絕對numerical誤差會減少 25% ，但這似乎并沒有轉化為comparison誤差率的降低。

不過，以上幾點實際上并不重要，因為這里真正重要的結果是：反向 Z 映射基本上是神奇的。過來看：

在本測試中，帶浮動深度緩沖器的反向 -Z 給出零錯誤率。現在，如果您繼續收緊輸入深度值的間距，當然可以使其產生一些錯誤。不過，與其他任何選項相比，帶浮點數的反向 Z 更精確，令人可笑。

帶整數深度緩沖區的反向 -Z 與任何其他整數選項一樣好。

反向 Z 消除了預合成與單獨視圖/投影矩陣以及有限與無限遠平面之間的區別。換句話說，使用 reversed-Z ，您可以將投影矩陣與其他矩陣組合，并且可以使用您喜歡的遠平面，而不會影響精度。

我認為這里的結論是明確的。在任何透視投影情況下，只需使用帶反轉 Z 的浮點深度緩沖區！如果不能使用浮點深度緩沖區，則仍應使用 reversed-Z 。它不是解決所有精度問題的靈丹妙藥，尤其是在構建包含極端深度范圍的開放環境時。但這是一個很好的開始。

關于作者

Nathan Reed自 2008 年以來一直從事游戲和游戲相關領域的計算機圖形編程工作。目前，他致力于 Adobe 的 3D 和沉浸式工具。以前，他在 343 工業（光環無限）、索尼的吸盤沖壓工作室（臭名昭著的筑島幽靈）和 NVIDIA 工作。

審核編輯：郭婷