一條簡單的傳輸線

假設有一根位于地表面（或地平面，或信號地）上方的自由空間中的金屬線，如下圖所示。我們將對它進行更精確的定義。這屬于 TEM 傳輸線的范疇，意味著電場和磁場完全位于垂直于該線的平面內，并且坡印廷矢量與這條線處處平行。（非常嚴格地說，這是一條準 TEM 傳輸線，因為金屬線不是無限導電的，但正如我們將看到的，這一點對我們下面討論的內容并沒有任何影響）。

在電線的一端，有一個正弦時變源將接地層連接到電線，在電線的另一端，有一個電阻負載。雖然我們在實踐中并不經常看到這種精確的傳輸線，但它與微帶線非常相似。

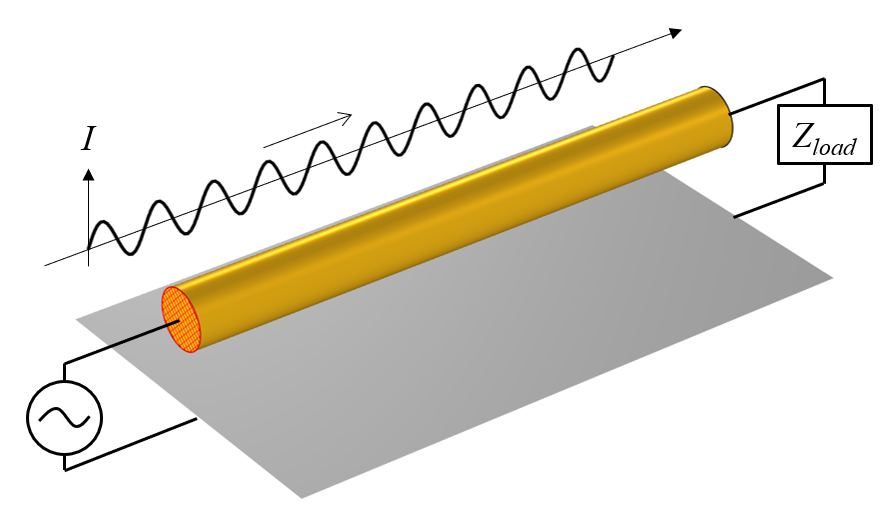
接地面上方的導線，一端是電源，另一端是負載，以及導線中某一時刻的總電流圖。

正弦時變源將驅動電流沿整個導線來回移動，通過電阻負載，然后進出接地平面。如果我們可以在任何時刻對電流進行快照，它看起來就像是從源到負載傳播的正弦波。

現在，當我們考慮流經導電材料的時變電流時，必須考慮集膚效應：即時變電流在導體外表面流動的趨勢。事實上，我們將假設激勵頻率很高，與導線的半徑相比，集膚深度非常非常小，小到我們看作電流是在導體的表面上流動，而不是在體積內流動，并且可以通過 阻抗 邊界條件對導線進行建模。這在以前的博文“模擬電磁波問題中的金屬對象”和“如何模擬時變磁場中的導體”中有過更加詳細的討論。

接下來，我們來看地表面?；叵胍幌挛覀冎暗亩x，在直流系統中，我們將接地定義為對電流沒有阻力的域（或者至少阻力很小，以至于與我們的建模目的無關），這里也適用類似的定義。接地是一個沒有電阻的域的邊界，或者它是一種完美的導電材料。然而，正如剛才所討論的，由于存在集膚效應，對于具有無限電導率的材料，集膚深度恰好為零，因此在接地線表面上將有電流流動。

地平面上的情況

現在，讓我們來討論以下直流系統和波狀場系統之間的巨大區別。在直流系統中，我們完全忽略了接地域內的電流；而波狀系統中存在沿這個地表面流動的電流，這些電流不能被忽略。下圖是這些電流以及一個導線橫截面上的電場和磁場在某個時刻的可視化效果圖。

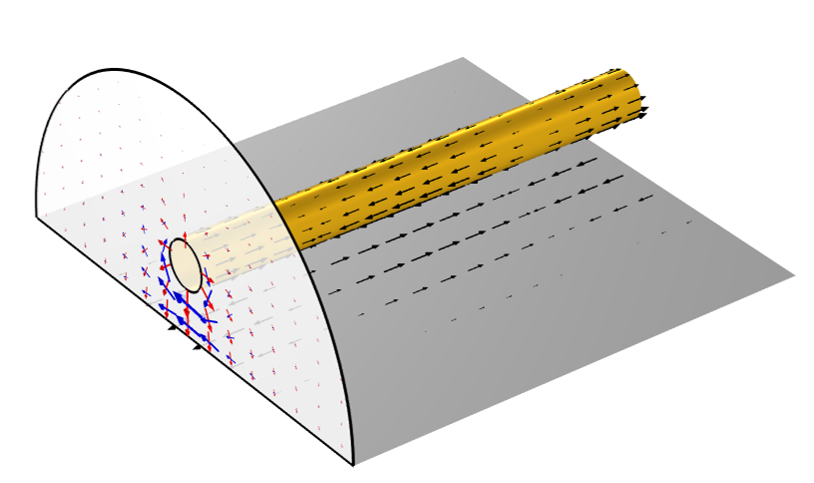
某一瞬間的電流（黑色）、電場（紅色）和磁場（藍色）的可視化箭頭。

也許有人會問：在一個有無限電導率的材料表面，怎么會有有限的電流？要回答這個問題，我們還需要看一下地平面上方的自由空間。這個自由空間有一個阻抗，而沿著材料表面流動的電流將取決于這個自由空間的阻抗。

這立即提出了一個非常重要的問題：我們必須考慮地平面上方有多少可用空間？事實證明，我們不僅要考慮地平面正上方的自由空間，還要考慮導線周圍的空間，甚至導線上方的一些空間區域。所有這些結構都會對傳輸線的阻抗產生影響。事實上，在建立這類數值模型時，需要研究要包括多少范圍的自由空間區域。COMSOL 案例庫中的確定平行傳輸線的阻抗教程模型對此有所討論。

由上述教程模型可知，這個完美電導體表面（我們稱之為地平面）上的電流會受到它上方所有空間的影響。另一種說法是這個完美電導體表面上的電流包含整個建?？臻g的圖像，這使我們對 PEC 地平面有了第二個解釋：它是一個對稱性條件。就好像平面的另一邊有一個等效的結構，而在那一邊，導線中的電流將指向相反的方向。

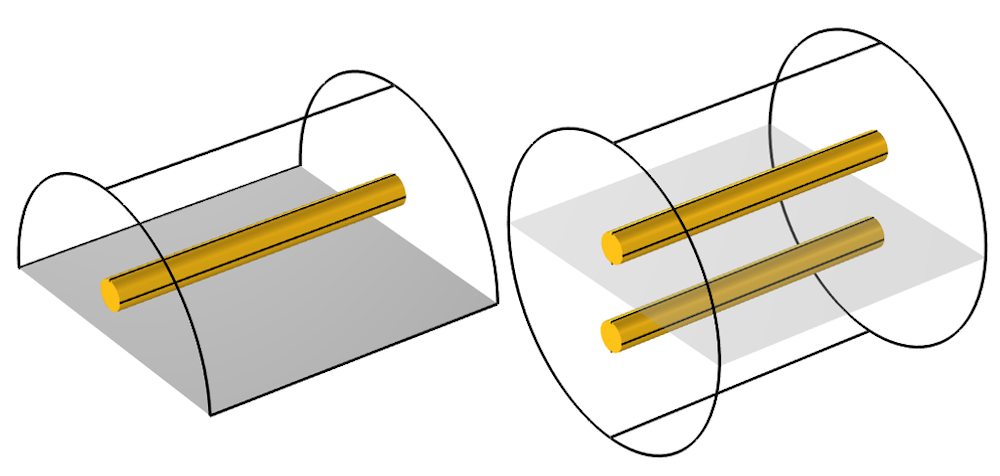
通過對稱性條件，地平面上方的導線模型等效于平行導線傳輸線的模型。

基于此，在電磁波的范圍內，我們現在可以開始做一些更精確的定義。地面是一個無損（完全導電，或完美電導體）的表面，有限的電流沿著它流動。沿著這個表面流動的電流將受到它上方所有結構的影響。如果這個完美電導體表面在建模空間的一側描述了一個平面，那么就相當于強加了一個對稱性條件。如果我們有兩個分離的完美電導體表面，可以任意選擇一個，并將其定義為接地。在某些情況下，我們還可以想出一個辦法來定義第二個完美半導體表面相對于這個接地的電勢差（電壓）。

在頻域中定義電壓

回想一下我們對穩態電流的討論，我們將電壓定義為任意兩點之間電場的路徑積分。對于穩態電流，電場是標量電勢的梯度，并且該積分始終與路徑無關。然而，對于電磁波，電場是波動方程的解，并且我們可以證明（通過一些我們將跳過的繁瑣矢量計算）這種電場的路徑積分與路徑無關，除了一些特殊情況。

其中一個特殊情況是，當沿著位于完美電導體表面的一條線進行路徑積分時。與表面相切的電場始終為零，因此沿該表面任何一條線的電場積分為零。然而，表面電流被定義為

，其中

由

計算，所以電流不為零，即使切向電場的積分為零。請注意，這里沒有矛盾；周圍環境的阻抗導致完美電導體表面的電流有限，且切向電場為零。

第二個要考慮的有趣情況是，當我們沿著垂直于TEM傳輸線軸線的平面上的一條線取電場的路徑積分時。根據定義，電場和磁場完全位于這個平面內，所以可以證明（通過一些我們將跳過的矢量計算）這個積分將與路徑無關。也就是說，我們可以在這個平面的各點之間定義一個電壓。因此，選擇一個接地表面上的點，并在傳輸線的電線上的另一點，進行任何路徑積分?，F在我們有一個電壓，對應于從信號分析儀得到的測量結果。我們也可以沿著完全分割接地和導線之間空間的線，對磁場進行路徑積分，得到沿傳輸線流動的電流。

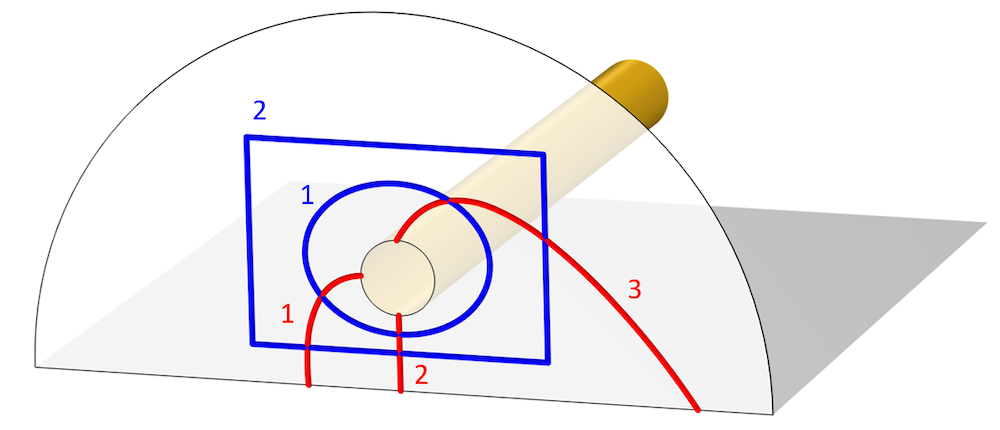
顯示電壓（紅色）和電流（藍色）的各種不同積分路徑的圖像。

最后，我們來討論這樣一個事實：由于導線的有限導電性，這實際上是一條準TEM線，可以通過 阻抗 邊界條件進行建模。在這種情況下，電場和磁場的平面外分量相對于平面內分量來說非常小，我們仍然可以安全地使用上述定義。

綜上，我們知道：

電壓是電場的路徑積分，但這只能在電場旋度為零或接近零的情況下進行評估：在 TEM 或準 TEM 傳輸線的橫截面上。

在 TEM 或準 TEM 傳輸線的橫截面上，電壓對應于通過信號分析儀物理測量的電壓。只有在這里，術語電壓在頻域電磁波模型中才有意義。

在 PEC 表面，我們可以沿著該表面上的路徑對電場進行積分，但是如果沿著不在該表面的路徑進行積分，可能會得到一個非零積分。另外，我們已經看到會有電流存在，所以兩點之間的零電壓差并不意味著零電流。因此，實際上，在這種情況下談論電壓幾乎沒有價值。如果我們試圖實際測量兩點之間的場，我們將不得不引入一個傳感器，包括這些點之間的某種傳輸線，但這會改變設備。

請將上述這些信息牢牢記在大腦中，這樣我們就可以自信地建模了。對于這里的情況，我們可以使用TEM 型的端口 邊界條件，將接地 和電勢 子特征應用于接地平面和電線的邊緣。COMSOL學習中心的一篇文章“對 TEM 和準 TEM 傳輸線進行建?！敝刑峁┝藢?TEM 類型傳輸線建模的所有其他選項的完整概述，您可以參考閱讀。

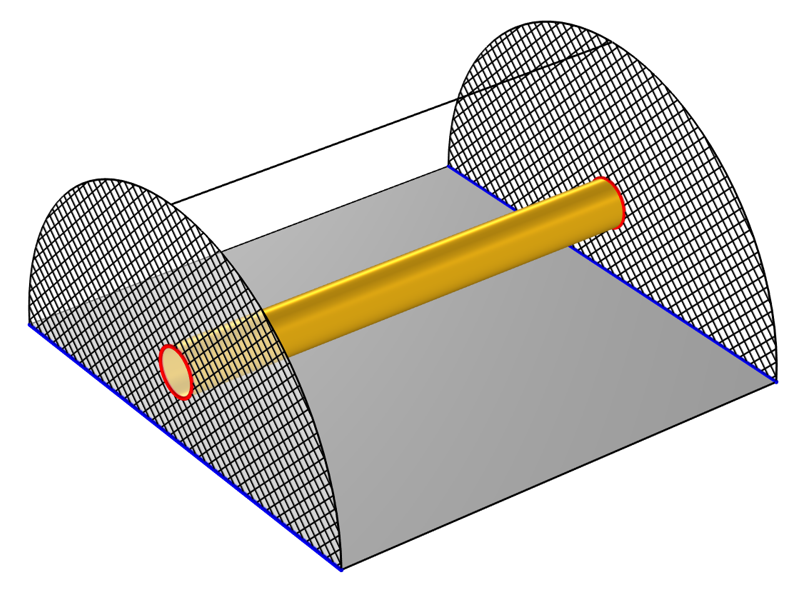
傳輸線模型的設置示意圖。兩端的兩個 TEM 端口（交叉陰影線）定義了接地（藍色）和電壓（紅色）。

結束語

現在你知道如何在頻域電磁波建模的背景下自信地使用電壓和接地這兩個術語了吧！我們可以把同樣的論點擴展到瞬態情況下，并得出同樣的結論。在時域建模中，接地是一個電流返回路徑，可以是一個對稱條件。

因此，對于任何時變模型，同時考慮電場和磁場，只能在評估 TEM 傳輸線橫截面的場的情況下談論電壓。盡管這句話很簡單，但這個我們必須遵循的論點對于理解電磁設備的建模非常有幫助。