在二叉樹之前的數(shù)據(jù)結(jié)構(gòu)學(xué)習(xí)中,我們學(xué)習(xí)了順序表、鏈表、棧、隊(duì)列這幾種結(jié)構(gòu),它們都是用鏈表或者數(shù)組的方式來實(shí)現(xiàn)的,主要考察我們對(duì)結(jié)構(gòu)體的運(yùn)用!
今天讓我們來學(xué)習(xí)一個(gè)新的數(shù)據(jù)結(jié)構(gòu),也就是下面這副圖里面的樹
是下面這個(gè)才對(duì)
1.什么是樹?
1.1樹的概念
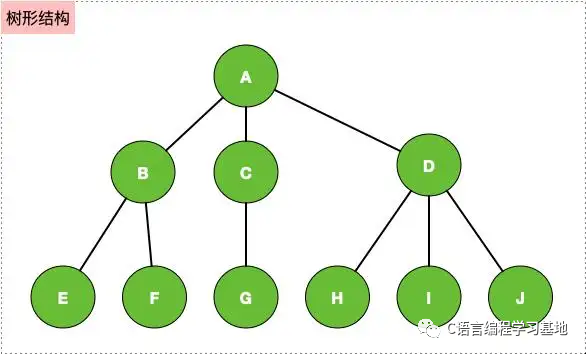
樹是一種非線性的數(shù)據(jù)結(jié)構(gòu),它是由n個(gè)有限節(jié)點(diǎn)組成的具有一定層次關(guān)系的集合。
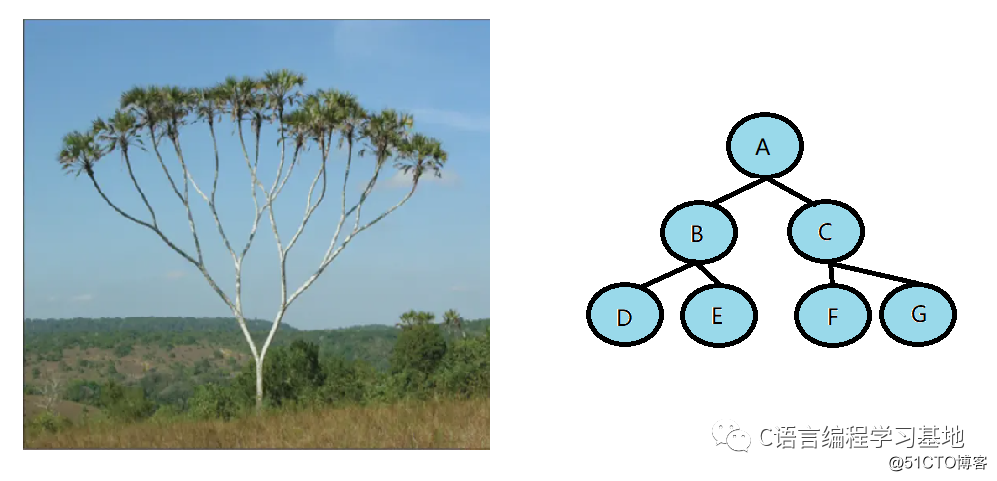
把它叫做樹是因?yàn)樗雌饋淼拇_像一個(gè)樹的根部
當(dāng)然也可以理解為是樹干在上,樹葉在下的結(jié)構(gòu)
有一個(gè)特殊的節(jié)點(diǎn),被稱為根節(jié)點(diǎn),也就是樹的開頭
除了根節(jié)點(diǎn)外,其余節(jié)點(diǎn)都是,個(gè)互不相交的集合。每一個(gè)集合都是一顆與樹的結(jié)構(gòu)類似的子樹
每一個(gè)節(jié)點(diǎn)只能有一個(gè)前驅(qū),但是可以有很多個(gè)后驅(qū)
因此,樹是遞歸定義的
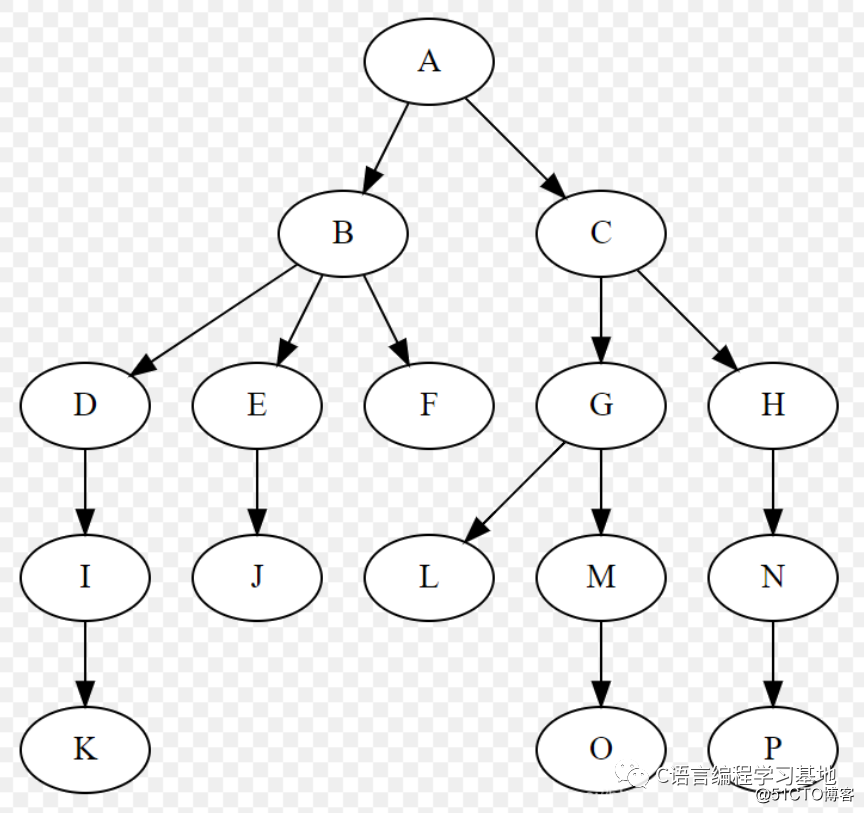
樹中的子節(jié)點(diǎn)不能有交集
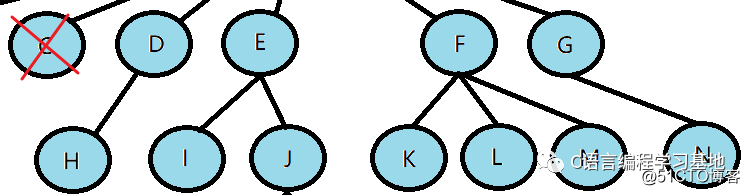
上圖中的B節(jié)點(diǎn)不能有G這個(gè)孩子,因?yàn)镚已經(jīng)有父母C了
同理,G節(jié)點(diǎn)也不能同時(shí)擁有兩對(duì)父母
子節(jié)點(diǎn)之間也不能相連,如E和F不能相連
1.2樹的相關(guān)知識(shí)點(diǎn)
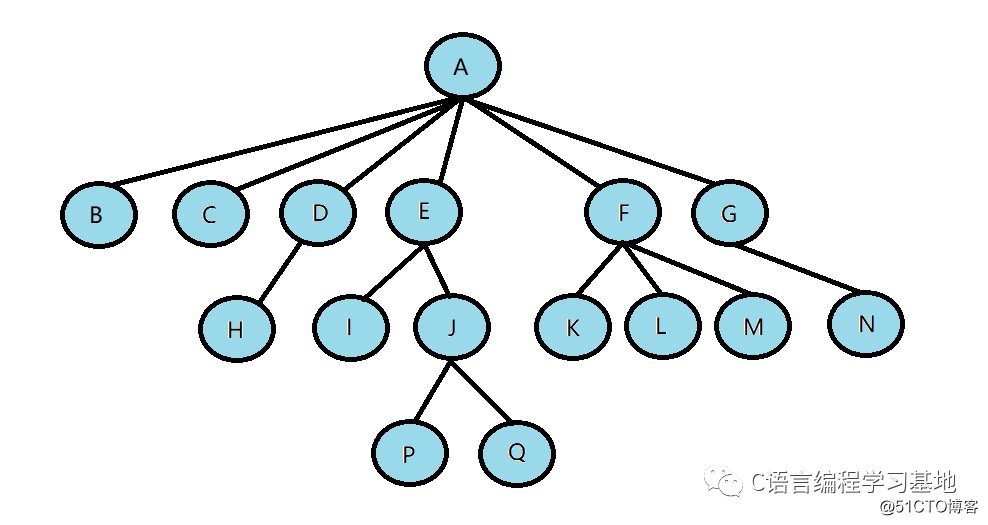
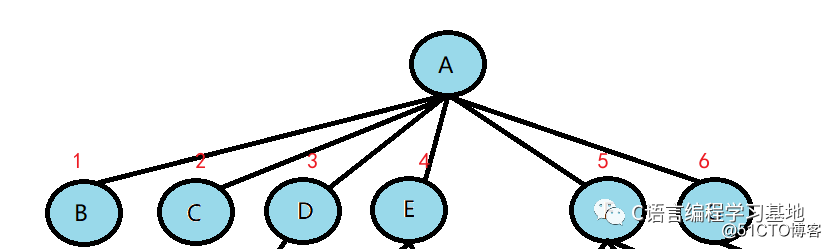
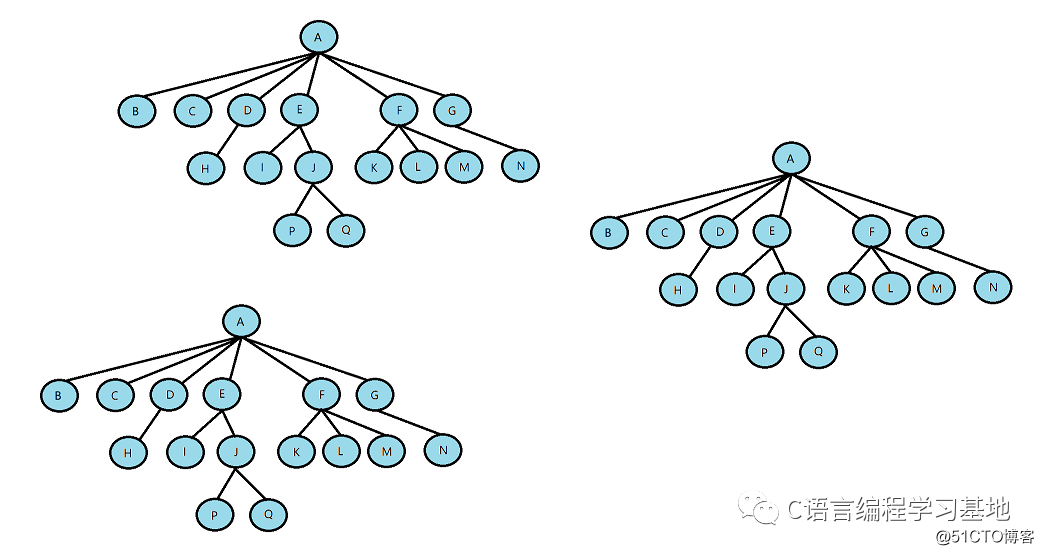
節(jié)點(diǎn)的度:一個(gè)節(jié)點(diǎn)含有的子樹的個(gè)數(shù)稱為該節(jié)點(diǎn)的度;如下圖:A的度為6
葉節(jié)點(diǎn)或終端節(jié)點(diǎn):度為0的節(jié)點(diǎn)稱為葉節(jié)點(diǎn);圖中B、C、H、I…等節(jié)點(diǎn)為葉節(jié)點(diǎn)
非終端節(jié)點(diǎn)或分支節(jié)點(diǎn):度不為0的節(jié)點(diǎn);如上圖中D、E、F、G…等節(jié)點(diǎn)為分支節(jié)點(diǎn)
簡(jiǎn)單的說,就是有娃的節(jié)點(diǎn)就是分支節(jié)點(diǎn)
雙親節(jié)點(diǎn)或父節(jié)點(diǎn):若一個(gè)節(jié)點(diǎn)含有子節(jié)點(diǎn),則這個(gè)節(jié)點(diǎn)稱為其子節(jié)點(diǎn)的父節(jié)點(diǎn);如上圖,D是H的父節(jié)點(diǎn)
孩子節(jié)點(diǎn)或子節(jié)點(diǎn):一個(gè)節(jié)點(diǎn)含有的子樹的根節(jié)點(diǎn)稱為該節(jié)點(diǎn)的子節(jié)點(diǎn);如上圖:H是D的孩子節(jié)點(diǎn)
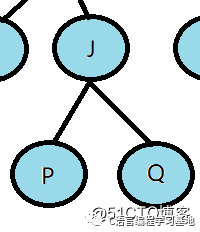
兄弟節(jié)點(diǎn):具有相同父節(jié)點(diǎn)的節(jié)點(diǎn)互稱為兄弟節(jié)點(diǎn);如下圖:P、Q是兄弟節(jié)點(diǎn)
樹的度:一棵樹中,最大的節(jié)點(diǎn)的度稱為樹的度;示例中樹的度為6(即A的度)
節(jié)點(diǎn)的層次:從根開始定義起,根為第1層,根的子節(jié)點(diǎn)為第2層,以此類推
樹的高度或深度:樹中節(jié)點(diǎn)的最大層次;示例中樹的高度為4
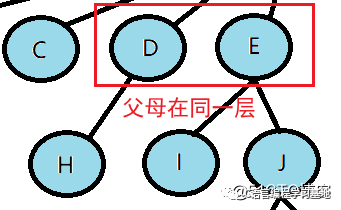
堂兄弟節(jié)點(diǎn):雙親在同一層的節(jié)點(diǎn)互為堂兄弟;如下圖:H、I互為兄弟節(jié)點(diǎn)
節(jié)點(diǎn)的祖先:從根到該節(jié)點(diǎn)所經(jīng)分支上的所有節(jié)點(diǎn);示例中A是所有節(jié)點(diǎn)的祖先
子孫:以某節(jié)點(diǎn)為根的子樹中任一節(jié)點(diǎn)都稱為該節(jié)點(diǎn)的子孫。示例中所有節(jié)點(diǎn)都是A的子孫
森林:由m(m>0)棵互不相交的樹的集合稱為森林
多個(gè)不相交的樹就是森林
1.3樹的代碼表示
表示樹的方式有很多種,比如下面這種
#define N 5 //指定樹的度為5struct TreeNode{ int data; struct TreeNode* subs[N];//用指針數(shù)組存放孩子節(jié)點(diǎn)的指針};
但這種方法不夠優(yōu),給大家展示一個(gè)用的最廣泛的方法——孩子兄弟表示法
typedef int DataType;struct Node{ struct Node* _firstChild1; // 第一個(gè)孩子結(jié)點(diǎn) struct Node* _pNextBrother; // 指向其下一個(gè)兄弟結(jié)點(diǎn) DataType _data; // 結(jié)點(diǎn)中的數(shù)據(jù)域};
通過這種方法,父親節(jié)點(diǎn)只需要保存它的第一個(gè)娃,其他娃就讓大娃的兄弟節(jié)點(diǎn)來找
也就是家長只用管老大,老大管老二,老二管老三,依次往下……
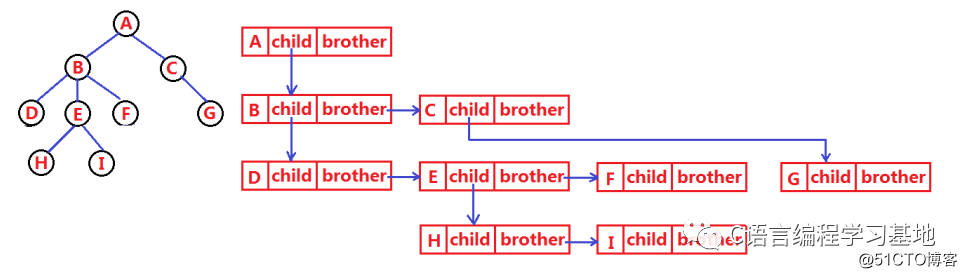
實(shí)際寫代碼的結(jié)構(gòu)大概是下圖這樣

2.二叉樹
在實(shí)際中,二叉樹是使用較多的一種樹的結(jié)構(gòu)
2.1概念
二叉樹是度為2的樹,它是一個(gè)特殊的樹
二叉樹不存在度大于2的節(jié)點(diǎn)
二叉樹是有序樹,它的娃(子樹)有左右之分,次序不能顛倒
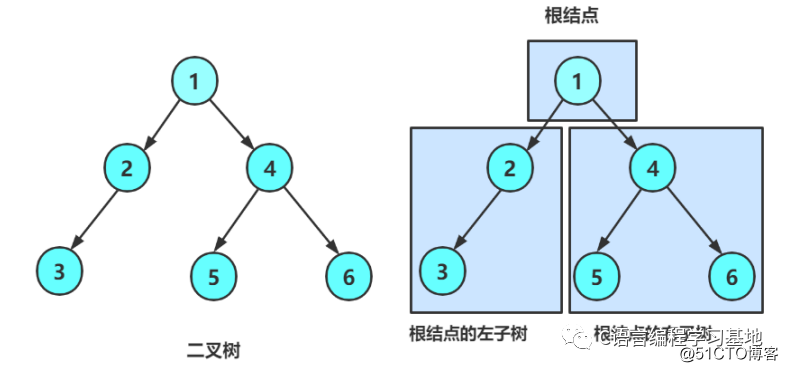
所以,二叉樹都是由下面各類節(jié)點(diǎn)組成的樹
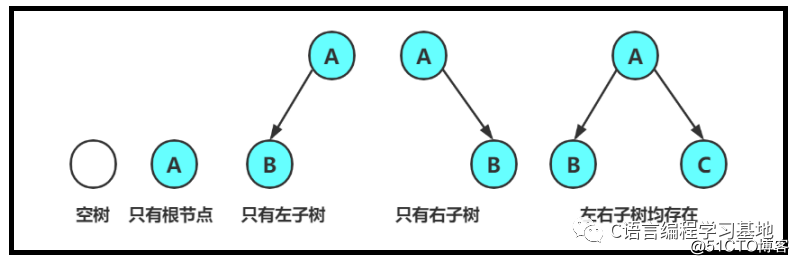
2.2特殊的二叉樹
滿二叉樹:如果每一個(gè)層的節(jié)點(diǎn)數(shù)都達(dá)到最大值,那這個(gè)二叉樹就是滿二叉樹。也就是說:滿二叉樹的層數(shù)為k,且節(jié)點(diǎn)總數(shù)是2k-1
滿二叉樹的節(jié)點(diǎn)數(shù)是一個(gè)等比數(shù)列公式
2 0 + 2 1 + 2 2 + . . . + 2 k ? 1 = 1 ? ( 1 ? 2 k ) / ( 1 ? 2 ) = 2 k ? 1 2^0+2^1+2^2+...+2^{k-1}=1*(1-2^k)/(1-2)=2^k -1 20+21+22+...+2k?1=1?(1?2k)/(1?2)=2k?1
完全二叉樹:完全二叉樹是效率很高的數(shù)據(jù)結(jié)構(gòu)。對(duì)于深度為K,有n個(gè)節(jié)點(diǎn)的二叉樹,當(dāng)且僅當(dāng)每一個(gè)節(jié)點(diǎn)都與深度為K的滿二叉樹中編號(hào)從1至n的節(jié)點(diǎn)一一對(duì)應(yīng)時(shí),稱為完全二叉樹。
簡(jiǎn)單說來,完全二叉樹的最后一層不一定滿,但必須要從左到右連續(xù)
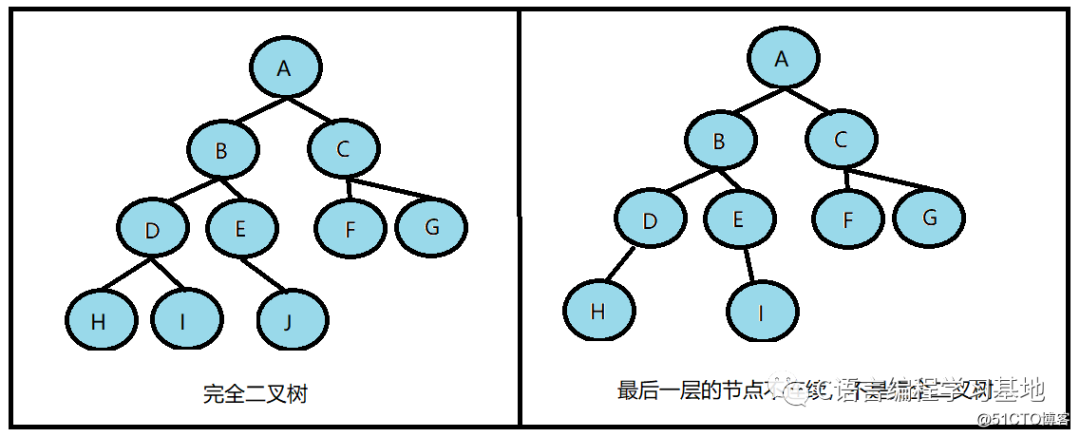
滿二叉樹是一個(gè)特殊的完全二叉樹
2.3二叉樹的性質(zhì)
若規(guī)定根節(jié)點(diǎn)的層數(shù)為1,則一棵非空二叉樹的第i層上最多有2(i-1)個(gè)結(jié)點(diǎn)
若規(guī)定根節(jié)點(diǎn)的層數(shù)為1,則深度為h的二叉樹的最大結(jié)點(diǎn)數(shù)是2h-1
對(duì)任何一棵二叉樹, 如果度為0其葉結(jié)點(diǎn)個(gè)數(shù)為n0, 度為2的分支結(jié)點(diǎn)個(gè)數(shù)為n2,則有n0 = n2+1
若規(guī)定根節(jié)點(diǎn)的層數(shù)為1,具有n個(gè)結(jié)點(diǎn)的滿二叉樹的深度,h=log2(n+1) 。(ps:是log以2為底,n+1為對(duì)數(shù))
對(duì)于具有n個(gè)結(jié)點(diǎn)的完全二叉樹,如果按照從上至下從左至右的數(shù)組順序?qū)λ泄?jié)點(diǎn)從0開始編號(hào),則對(duì)于序號(hào)為i的結(jié)點(diǎn)有:
若i>0,i位置節(jié)點(diǎn)的雙親序號(hào):(i-1)/2;i=0,i為根節(jié)點(diǎn)編號(hào),無雙親節(jié)點(diǎn)
若2i+1
若2i+2
2.4幾個(gè)選擇題
1. 某二叉樹共有 399 個(gè)結(jié)點(diǎn),其中有 199 個(gè)度為 2 的結(jié)點(diǎn),則該二叉樹中的葉子結(jié)點(diǎn)數(shù)為( )
A 不存在這樣的二叉樹
B 200 √
C 198
D 199
//葉子節(jié)點(diǎn)的數(shù)量 總比度為2的節(jié)點(diǎn)多1
2.在具有 2n 個(gè)結(jié)點(diǎn)的完全二叉樹中,葉子結(jié)點(diǎn)個(gè)數(shù)為( )
A n √
B n+1
C n-1
D n/2
//N0+N1+N2=2n
//2N0+N1-1=2n
//N1只有0和1兩種可能,因?yàn)閚為整數(shù),2n為偶數(shù),所以2N0=2n,N0=n
3.一棵完全二叉樹的節(jié)點(diǎn)數(shù)位為531個(gè),那么這棵樹的高度為( )
A 11
B 10 √
C 8
D 12
//假設(shè)高度是h
//完全二叉樹節(jié)點(diǎn)最多2^h -1
// 最少2^(h-1)-1 +1
//可以通過這兩個(gè)公式,推斷出h=10
3.二叉樹的存儲(chǔ)結(jié)構(gòu)
二叉樹一般可以使用兩種結(jié)構(gòu)存儲(chǔ),一種順序結(jié)構(gòu),一種鏈?zhǔn)浇Y(jié)構(gòu)
3.1順序存儲(chǔ)
順序結(jié)構(gòu)存儲(chǔ)就是使用數(shù)組來存儲(chǔ)
一般使用數(shù)組只適合表示完全二叉樹,因?yàn)椴皇峭耆鏄鋾?huì)有空間的浪費(fèi)。
現(xiàn)實(shí)使用中只有堆才會(huì)使用數(shù)組來存儲(chǔ)
下一篇博客會(huì)帶大家認(rèn)識(shí)堆這個(gè)特殊的樹形結(jié)構(gòu)(和內(nèi)存里面那個(gè)堆????沒啥關(guān)系哈)
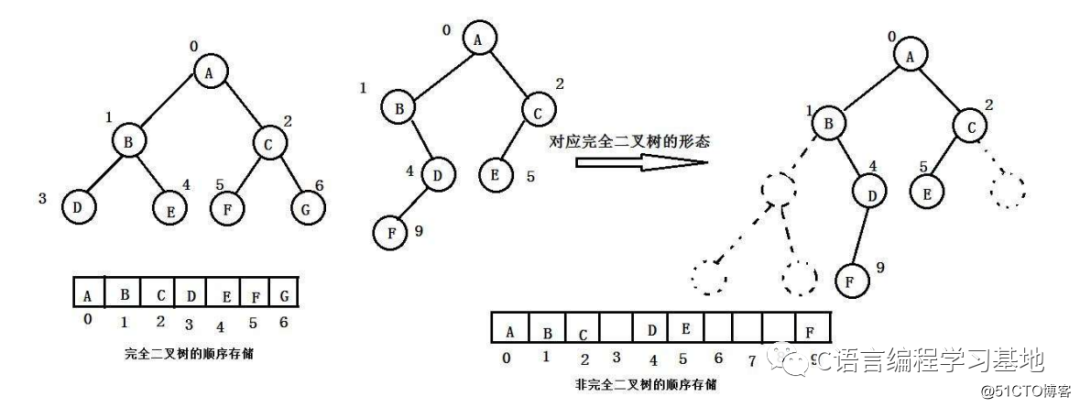
看到這張圖,你肯定想問,如果用數(shù)組結(jié)構(gòu)存儲(chǔ),那還怎么還原出一顆樹????呢?
這里我們需要理解物理存儲(chǔ)和邏輯結(jié)構(gòu)的關(guān)系
二叉樹順序存儲(chǔ)在物理上是一個(gè)數(shù)組,在邏輯上是一顆二叉樹
那怎么計(jì)算這種情況下的父親和娃呢?
leftchild=parent*2+1
rightchild=parent*2+2
parent=(child-1)/2
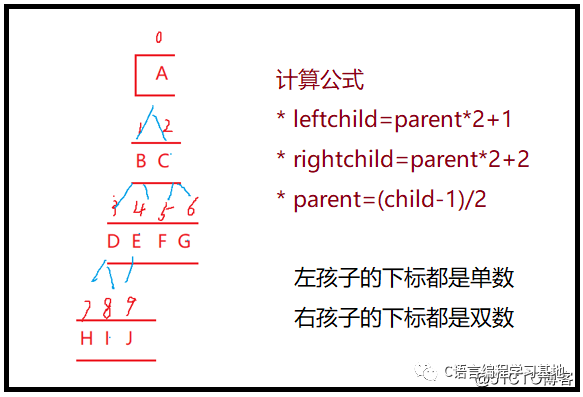
怎么樣,是不是忽然感覺妙級(jí)了?
3.2鏈?zhǔn)酱鎯?chǔ)
這就就沒啥好說的啦,使用一個(gè)簡(jiǎn)單的二叉鏈就能構(gòu)成二叉樹
typedef int BTDataType;// 二叉鏈struct BinaryTreeNode{ struct BinTreeNode* _pLeft; // 指向當(dāng)前節(jié)點(diǎn)左孩子 struct BinTreeNode* _pRight; // 指向當(dāng)前節(jié)點(diǎn)右孩子 BTDataType _data; // 當(dāng)前節(jié)點(diǎn)的值}
審核編輯 :李倩
-
C語言
+關(guān)注
關(guān)注
180文章
7633瀏覽量
141994 -
數(shù)據(jù)結(jié)構(gòu)
+關(guān)注
關(guān)注
3文章
573瀏覽量
40780 -
二叉樹
+關(guān)注
關(guān)注
0文章
74瀏覽量
12655
原文標(biāo)題:C語言數(shù)據(jù)結(jié)構(gòu):什么是樹?什么是二叉樹?
文章出處:【微信號(hào):cyuyanxuexi,微信公眾號(hào):C語言編程學(xué)習(xí)基地】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
C語言精彩編程百例-364頁
程序設(shè)計(jì)與數(shù)據(jù)結(jié)構(gòu)
深入理解C語言:C語言循環(huán)控制

C語言中結(jié)構(gòu)體與聯(lián)合體的深度解析:內(nèi)存布局與應(yīng)用場(chǎng)景
C++學(xué)到什么程度可以找工作?
全套C語言培訓(xùn)資料—PPT課件
分析C語言代碼結(jié)構(gòu)的設(shè)計(jì)問題
嵌入式學(xué)習(xí)-飛凌嵌入式ElfBoard ELF 1板卡-初識(shí)設(shè)備樹之設(shè)備樹組成和結(jié)構(gòu)
飛凌嵌入式ElfBoard ELF 1板卡-初識(shí)設(shè)備樹之設(shè)備樹組成和結(jié)構(gòu)
DDC264配置寄存器數(shù)據(jù)寫入和320 DCLK時(shí)鐘脈沖后的回讀數(shù)據(jù)結(jié)構(gòu)是什么?
視覺軟件HALCON的數(shù)據(jù)結(jié)構(gòu)
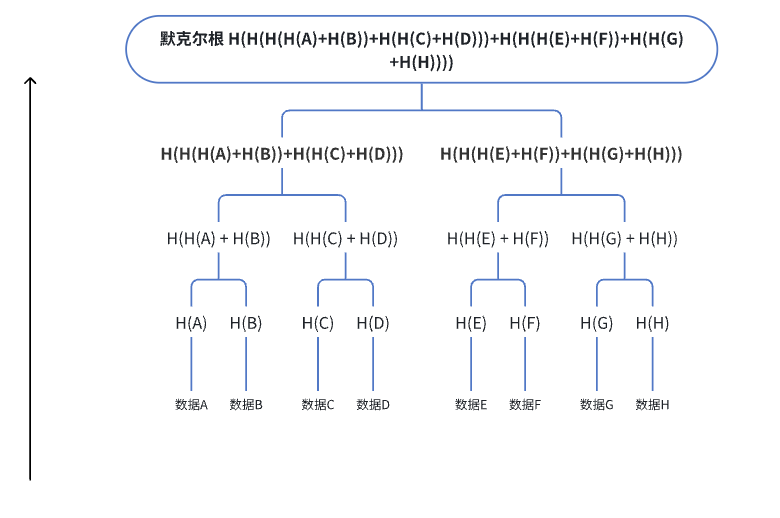
什么是默克爾樹(Merkle Tree)?如何計(jì)算默克爾根?



















評(píng)論