擬或 合成數據 生成是人工智能工具發展的一個重要趨勢。傳統上，這些數據集可用于解決低數據問題或邊緣情況場景，而或許現在存在于可用的實際數據集中。

合成數據的新興應用包括建立模型性能水平、量化適用領域，以及下一代系統工程，其中人工智能模型和傳感器是串聯設計的。

圖 1 。 船舶合成孔徑雷達渲染： 相位圖 （ left ） ，壓縮圖像 （ right ）。

Blender 是生成這些數據集的一個常用且引人注目的工具。它是免費使用和開源的，但同樣重要的是，它可以通過強大的 Python API 完全擴展。 Blender 的這一特性使其成為視覺圖像渲染的一個有吸引力的選擇。因此，它已被廣泛用于此目的，有 18 +渲染引擎選項可供選擇。

集成到 Blender 中的渲染引擎（如 Cycles ）通常具有緊密集成的 GPU 支持，包括最先進的 NVIDIA RTX 支持。但是，如果在可視化渲染引擎之外需要高性能級別，例如合成 SAR 圖像的渲染，那么 Python 環境對于實際應用程序來說可能過于遲緩。加速這段代碼的一個選擇是使用流行的 Numba 包將 Python 代碼的部分預編譯成 C 。然而，這仍有改進的余地，特別是在采用領先的 GPU 體系結構進行科學計算方面。

GPU 科學計算功能可直接從 Blender 中獲得，允許使用簡單的統一工具，利用 Blender 強大的幾何體創建功能以及尖端計算環境。對于 blender2 。 83 +的最新變化，可以使用 CuPy （一個專門用于數組計算的 GPU 加速 Python 庫）直接從 Python 腳本中完成。

根據這些想法，下面的教程將比較兩種不同的加速矩陣乘法的方法。第一種方法使用 Python 的 Numba 編譯器，而第二種方法使用 NVIDIA GPU-compute API， CUDA 。這些方法的實現可以在 rleonard1224/matmul GitHub repo 中找到，還有一個 Dockerfile ，它設置了 anaconda 環境，從中可以運行 CUDA – 加速的 Blender Python 腳本。

矩陣乘法算法

作為討論用于加速矩陣乘法的不同方法的前奏，我們簡要回顧了矩陣乘法本身。

對于兩個矩陣的乘積[A*B]為了更好地定義[A]必須等于[B].

[A]然后是一個矩陣[m]行和[n]列，即[m*n]matrix.

[B]是一個[n*p]matrix.

產品[C=A.B]結果是[m*p]matrix.

如果[C],[A],和[B]使用數字 1 （即基于 1 的索引）進行索引，然后是的第 i 行和第 j 列中的元素[C],[C[i,j]],

由以下公式確定：

麻木加速度

通過使用 Numba 。 jit decorator ，可以將 Numba 編譯器應用于 Python 腳本中的函數。通過預編譯到 C 中，在 Python 代碼中使用 numba 。 jit decorator 可以顯著減少循環的運行時間。由于直接轉換為代碼的矩陣乘法需要嵌套 for 循環，因此使用 numba 。 jit decorator 可以顯著減少用 Python 編寫的矩陣乘法函數的運行時間。 matmulnumba.py Python 腳本實現矩陣乘法并使用 numba 。 jit decorator 。

CUDA 加速度

在討論使用 CUDA 加速矩陣乘法的方法之前，我們應該大致概述 CUDA 內核的并行結構。內核啟動中的所有并行進程都屬于一個網格。網格由塊數組組成，每個塊由線程數組組成。網格中的線程組成了由 CUDA 內核啟動的基本并行進程。圖 2 概述了這類并行結構的示例。

圖 2 。 一個由 2 組成的 CUDA 核網格的并行結構× 2 塊數組。每個塊由一個 2 × 2 個線程陣列。

既然已經詳細說明了 CUDA 內核啟動的并行結構，那么在 matmulcuda.py Python 腳本中用于并行化矩陣乘法的方法可以描述如下。

假設以下由一個由塊的二維數組組成的 CUDA 內核網格計算，每個塊由線程的一維數組組成：

矩陣積[C=A.B]

[A]and[m*n]matrix

[B]and[n*p]matrix

[C]and[m*p]matrix

此外，進一步假設如下：

網格 x 維中的塊數 （[nblocksx]） 大于或等于[m]([nblocksx≥m])。

網格 y 維中的塊數 （[nblocksy]） 大于或等于[p]([nblocksy≥p])。

每個塊中的線程數 （[ntheads]) 大于或等于[n]([ntheads≥n])。

矩陣積的元素[C=A.B]可以通過為每個塊分配一個元素的計算來并行計算[C],[C[i,j].

您可以通過將指定給要執行的塊的每個線程來獲得進一步的并行增強[C],[C[i,j]分配，計算[n]和等于[C],[C[i,j].

為了避免競爭條件，這些[n]積和結果的賦值[C],[C[i,j]可以使用 CUDA atomicAdd 函數處理。 atomicAdd 函數簽名由作為第一個輸入的指針和作為第二個輸入的數值組成。該定義將輸入的數值與第一個輸入所指向的值相加，然后將該和存儲在第一個輸入所指向的位置。

假設[C]初始化為零[tid(i,j)]表示屬于塊的線程的線程索引，其索引在塊的網格中[(i,j)]. 上述平行排列可通過以下方程式進行總結：

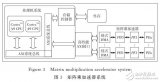
圖 3 總結了兩個樣本矩陣乘法的并行排列[2*2].

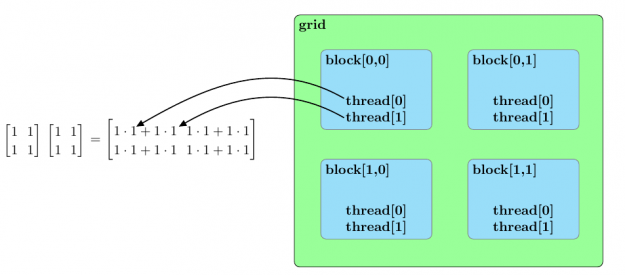
圖 3 。兩個 2 的乘法的并行化方法× 2 個矩陣。每個塊被分配兩個矩陣乘積的一個元素，一個線程塊中的線程并行地計算乘積，以確定分配給塊的矩陣元素的值。

提速

圖 4 顯示了 CUDA 加速矩陣乘法相對于不同大小矩陣的 Numba 加速矩陣乘法的加速比。在該圖中，繪制了加速比以計算兩個[N*N]兩個矩陣的所有元素都等于一的矩陣。[N]范圍從一百到一千，增量為一百。

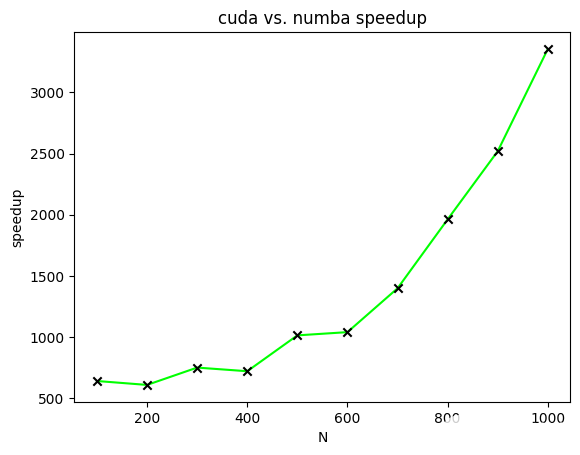
圖 4 。兩個 NxN 矩陣相乘時 CUDA 加速矩陣相乘相對于 Numba 加速矩陣相乘的加速比。

今后的工作

考慮到 Blender 作為計算機圖形工具的作用，一個適用于 CUDA 加速的相關應用領域涉及到通過光線跟蹤解決可見性問題。可見性問題可以概括如下： 相機存在于空間的某個點上，并且正在觀察由三角形元素組成的網格。可見性問題的目標是確定哪些網格元素對攝影機可見，哪些網格元素被其他網格元素遮擋。

光線跟蹤可以用來解決可見性問題。您試圖確定其可見性的網格由[N]網格元素。那樣的話，[N]可以生成以場景中的攝影機為原點的光線。這些端點位于[N]網格元素。

每條光線在不同的網格元素上都有一個端點。如果光線到達其端點時未被其他網格元素遮擋，則可以從攝影機中看到端點網格元素。圖 5 顯示了這個過程。

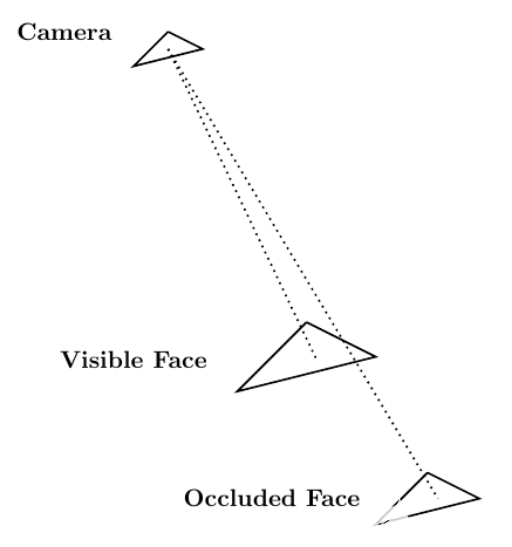
圖 5 。 從相機向場景中的人臉發射的兩條光線；一個面可見，另一個面被遮擋。

使用光線跟蹤來解決可見性問題的本質使其成為

作為直接計算實現時的問題。幸運的是， NVIDIA 開發了一個光線跟蹤庫，名為 NVIDIA OptiX ，它使用 GPU 并行性來實現顯著的加速。在 Blender Python 環境中使用 NVIDIA OptiX 將帶來實實在在的好處。

概括

這篇文章描述了兩種不同的加速矩陣乘法的方法。第一種方法使用 Numba 編譯器來減少 Python 代碼中與循環相關的開銷。第二種方法使用 CUDA 并行化矩陣乘法。速度比較證明了 CUDA 在加速矩陣乘法方面的有效性。

因為前面描述的 CUDA 加速代碼可以作為 Blender Python 腳本運行，所以可以在 Blender Python 環境中使用 CUDA 加速任意數量的算法。這大大提高了 blenderpython 作為科學計算工具的有效性。

關于作者

Eric Leonard 博士獲得了博士學位。在馬里蘭大學機械工程系，他專門從事理論和計算流體力學。研究生畢業后，他在馬薩諸塞州劍橋市的三菱 Ele CTR ic 研究實驗室實習，致力于開發一種替代傳統計算流體力學算法的方法。在 Rendered 。 AI ，他使用 CUDA 加速了合成孔徑雷達仿真代碼庫。

Nathan Kundtz 博士是物理學家、工程師和企業家。他與建筑公司、杜克大學以及眾多其他組織合作，尋找并建立大公司。 Kundtz 博士擁有電子工程碩士學位和博士學位。來自杜克大學物理系。他的工作涵蓋了人工智能、超材料、微波器件和低溫凝聚態物理。著有或合著專利及專利申請 40 余項，同行評議出版物 30 余篇；包括獲獎的博士研究。 Kundtz 博士被 LinkedIn 評為 40 歲以下十大科技專業人士之一。他是高盛 100 位最具吸引力的企業家之一， 40 歲以下的 Puget Sound ，并入選杜克大學研究生院為數不多的 Glasson 社團。

Ethan Sharratt 是 Rendered.AI 的軟件工程總監。他有一個學士學位，在華盛頓大學的 EDE CTR 工程，目前正在一個碩士。他擁有 10 年在具有挑戰性的環境中構建軟件和固件解決方案的經驗，包括開發空間等級軟件定義的無線電、信號和圖像處理以及實時計算機視覺管道。

Steven Forsyth 是 NVIDIA 的解決方案架構師，專注于支持聯邦生態系統。他在激光干涉儀引力波天文臺工作了幾年，在那里他獲得了信號處理和高性能計算方面的經驗。在 NVIDIA ，他將從 LIGO 獲得的知識與深度學習的知識結合起來，專門從事深度學習應用，涉及廣泛的領域，包括計算機視覺和網絡安全。史蒂文最近從喬治亞理工學院畢業，在那里他獲得了物理學學士學位。

審核編輯：郭婷