首先就是大腸包小腸，這就是軸的概念，除了這個還真的沒有什么別的想法。

最近用numpy，越用這個東西越發(fā)現(xiàn)一些基礎(chǔ)概念不明朗，這里簡單的記錄一下。

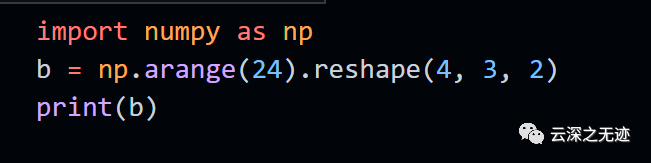
先生成一個三維的數(shù)組

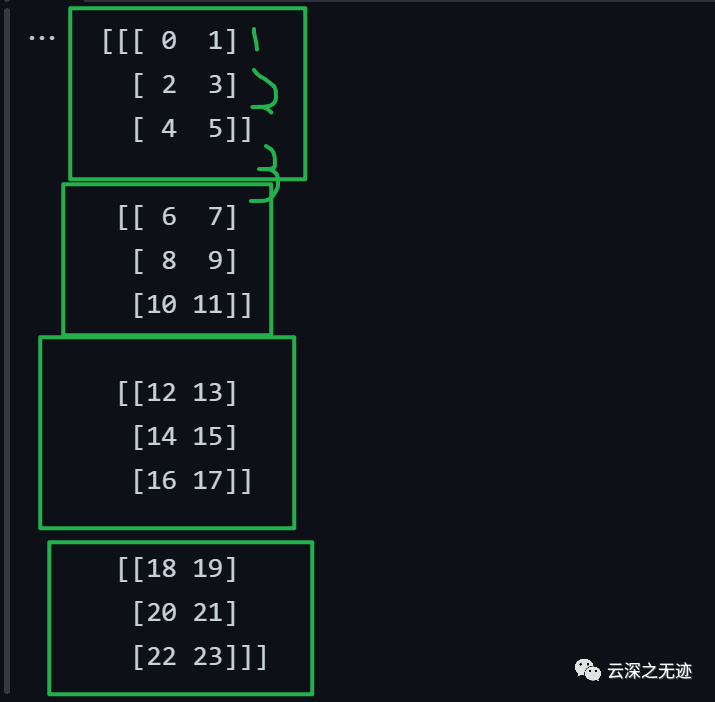
打印出來的樣子

從內(nèi)最小的開始看起，分別是元素，2，3，4

以小[]來界定

也就是說，首先是一個特別大的整體，一個數(shù)組，接著是里面4個小數(shù)組，每一個小數(shù)組里面有3個小數(shù)組，小數(shù)組內(nèi)的單元是一個數(shù)對來構(gòu)成的。

其實這就是軸的概念，只是因為是扁平化的，不直觀。

axis=2

axis=1

axis=0

按照順序來填充

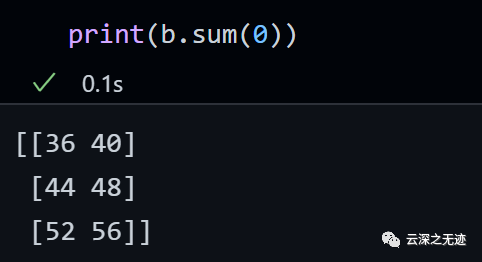
按照數(shù)組0軸來相加

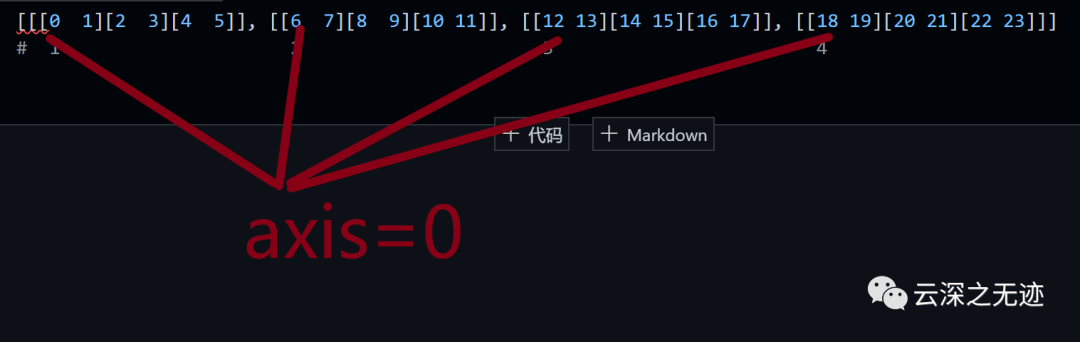
就是加的這個位置的元素

[[0+ 6+12+18=36 1+ 7+13+19=40] [2+ 8+14+20=44 3+ 9+15+21=48] [4+10+16+22=52 5+11+17+23=56]]

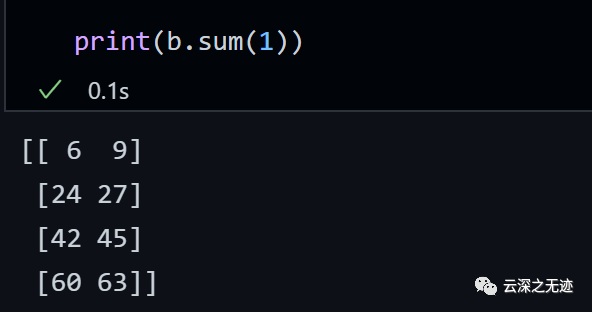
再看一個

就是這樣吧

[[ 0+ 1=1 2+ 3=5 4+ 5=9] [ 6+ 7=13 8+ 9=17 10+11=21] [12+13=25 14+15=29 16+17=33] [18+19=37 20+21=41 22+23=45]]

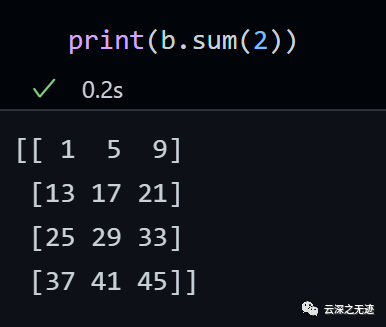
這個就沒有什么好說的了吧

其中第一軸是最大的稱為0號，

其次開始從左到右依次的放置

NumPy數(shù)組的維數(shù)稱為秩（rank），一維數(shù)組的秩為1，二維數(shù)組的秩為2，以此類推。在NumPy中，每一個線性的數(shù)組稱為是一個軸（axes），秩其實是描述軸的數(shù)量。比如說，二維數(shù)組相當于是兩個一維數(shù)組，其中第一個一維數(shù)組中每個元素又是一個一維數(shù)組。所以一維數(shù)組就是NumPy中的軸（axes），第一個軸相當于是底層數(shù)組，第二個軸是底層數(shù)組里的數(shù)組。而軸的數(shù)量——秩，就是數(shù)組的維數(shù)。

NumPy的數(shù)組中比較重要ndarray對象屬性有：

1.ndarray.ndim：數(shù)組的維數(shù)（即數(shù)組軸的個數(shù)），等于秩。最常見的為二維數(shù)組（矩陣）。

2.ndarray.shape：數(shù)組的維度。為一個表示數(shù)組在每個維度上大小的整數(shù)元組。例如二維數(shù)組中，表示數(shù)組的“行數(shù)”和“列數(shù)”。ndarray.shape返回一個元組，這個元組的長度就是維度的數(shù)目，即ndim屬性。

3.ndarray.size：數(shù)組元素的總個數(shù)，等于shape屬性中元組元素的乘積。

4.ndarray.dtype：表示數(shù)組中元素類型的對象，可使用標準的Python類型創(chuàng)建或指定dtype。另外也可使用前一篇文章中介紹的NumPy提供的數(shù)據(jù)類型。

5.ndarray.itemsize：數(shù)組中每個元素的字節(jié)大小。例如，一個元素類型為float64的數(shù)組itemsiz屬性值為8(float64占用64個bits，每個字節(jié)長度為8，所以64/8，占用8個字節(jié)），又如，一個元素類型為complex32的數(shù)組item屬性為4（32/8）。

6.ndarray.data：包含實際數(shù)組元素的緩沖區(qū)，由于一般通過數(shù)組的索引獲取元素，所以通常不需要使用這個屬性。

其實進一步的，是闡述了一種方向的問題：在二維數(shù)組中axis=0是按列的，axis=1意味著按行。

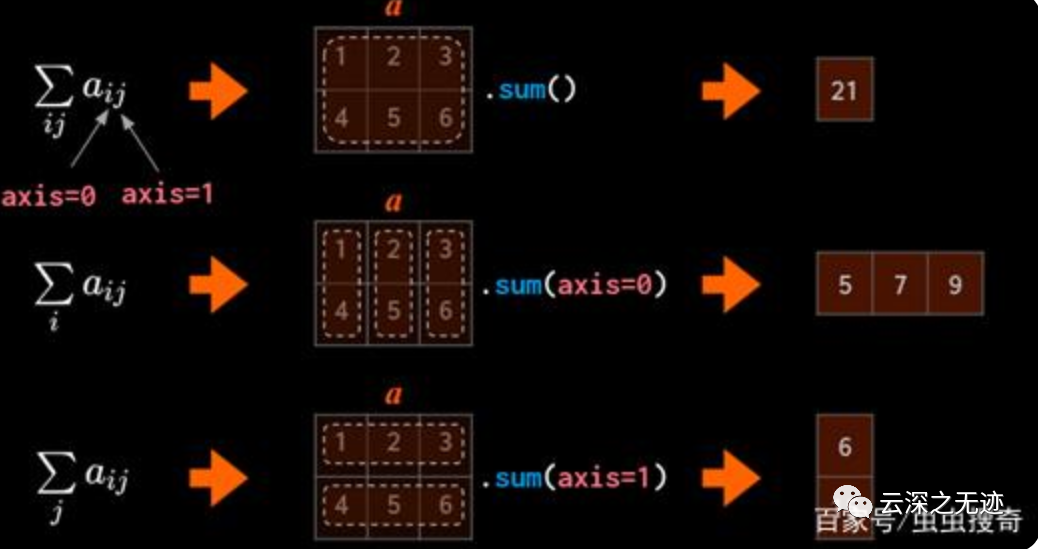
這個圖太漂亮了

事實上，到這里的時候還是沒有說明白主要的軸到底是怎么出來的，那繼續(xù)。

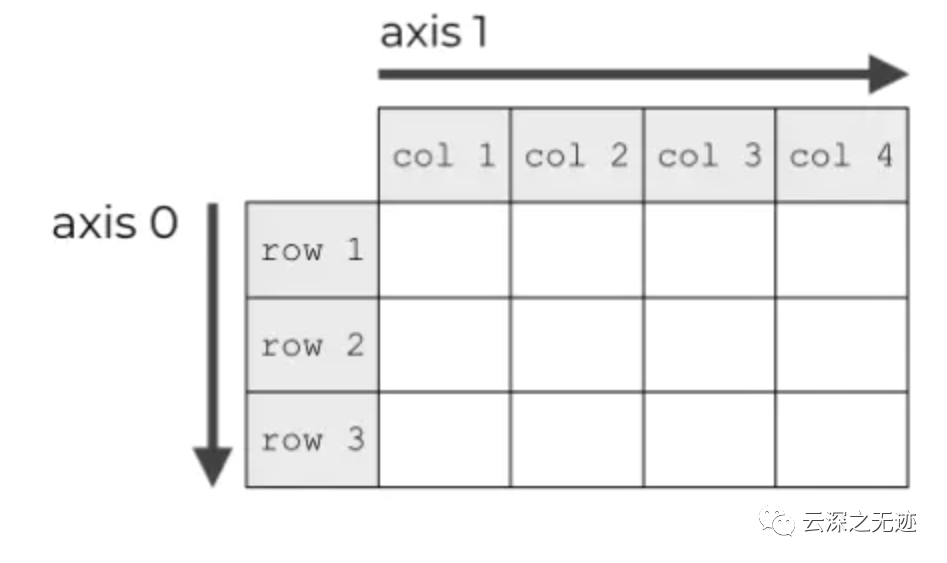
軸是行列的方向

如果是多維的數(shù)組，那axis=0就是向下的軸，axis=1是往右延的軸。

這些東西影響著你未來作用到上面的函數(shù)，該算哪些東西。而且進行計算的時候是會進行折疊，就是從這些指定的位置采用運算規(guī)律。

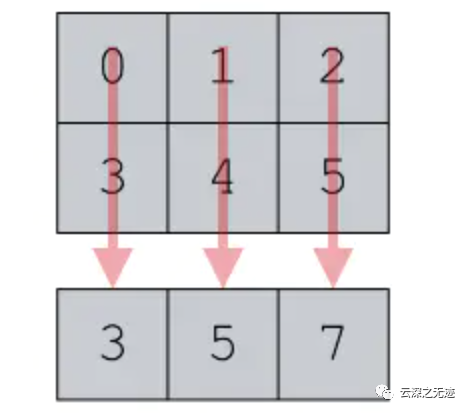
就是這樣的，加到一起，2就變成了1

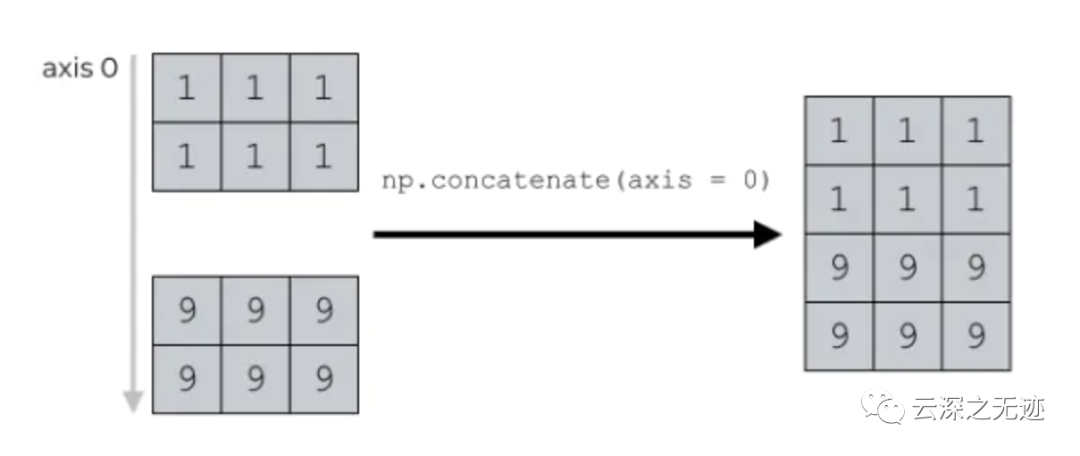
axis=0的拼接方式

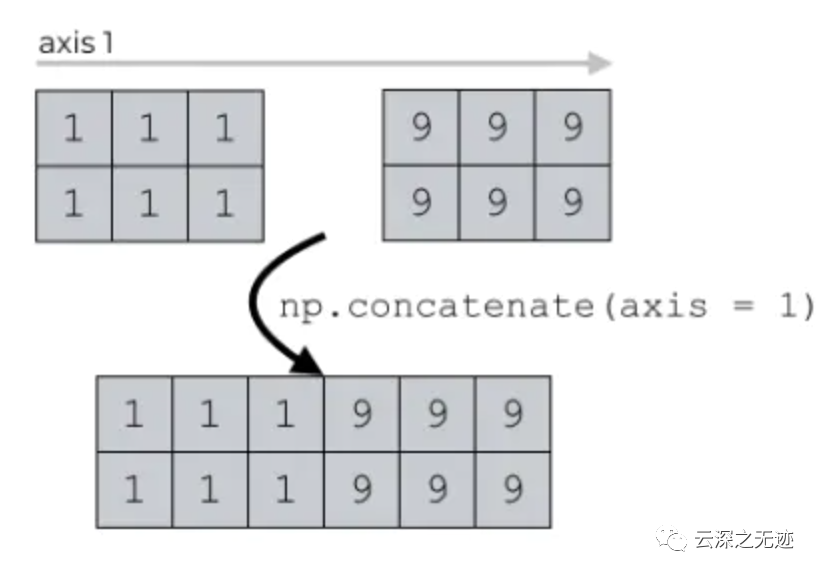
axis=1，橫向拼接

結(jié)論：將NumPy軸視為我們可以執(zhí)行操作的方向。

接下來再補充一些，別的理解，盡量我們一篇文章解決這個問題。

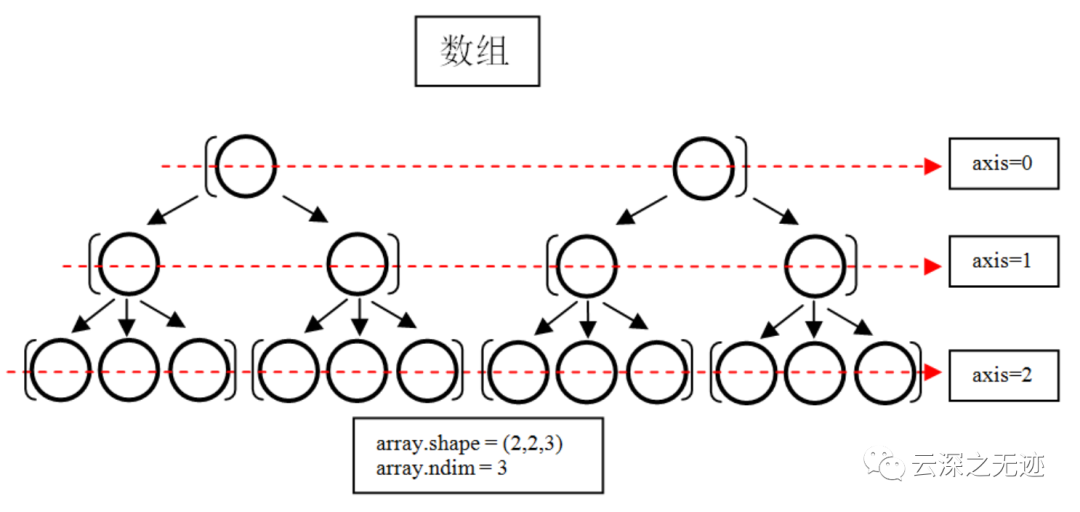
這個也是

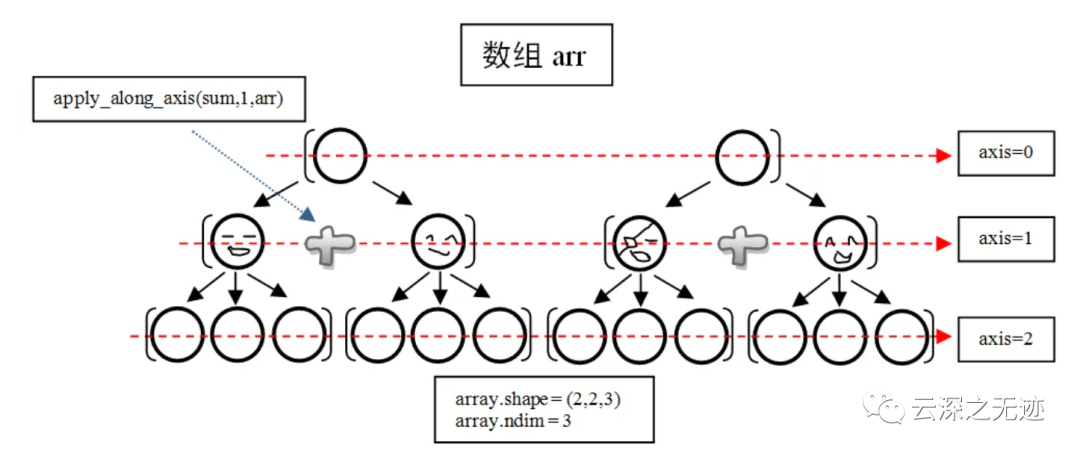
這個圖是讓我喜歡的不行，它清楚的展示了這個數(shù)組軸的包含關(guān)系

數(shù)組之間的算數(shù)關(guān)系

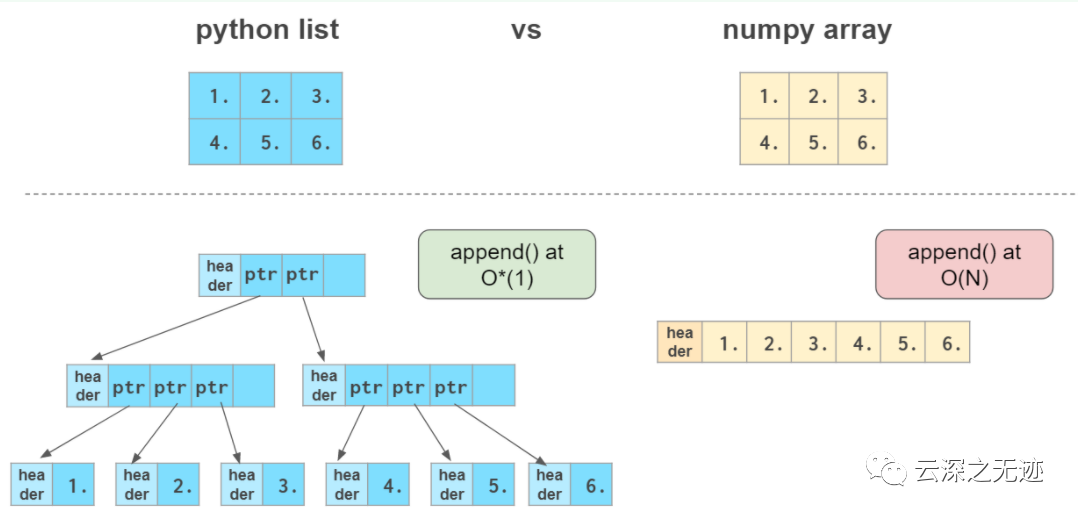
運算緊湊，使用了非動態(tài)的特性

使用Python的列表語法可以輕松的創(chuàng)建一個數(shù)組，要確保元素都一致

由于數(shù)組的原因，沒有了動態(tài)添加元素的特性，所以只能提前的把位置留好。

再有了變量的情況先，可以使用like函數(shù)生成一個相似的數(shù)組

提供了完整的生成函數(shù)

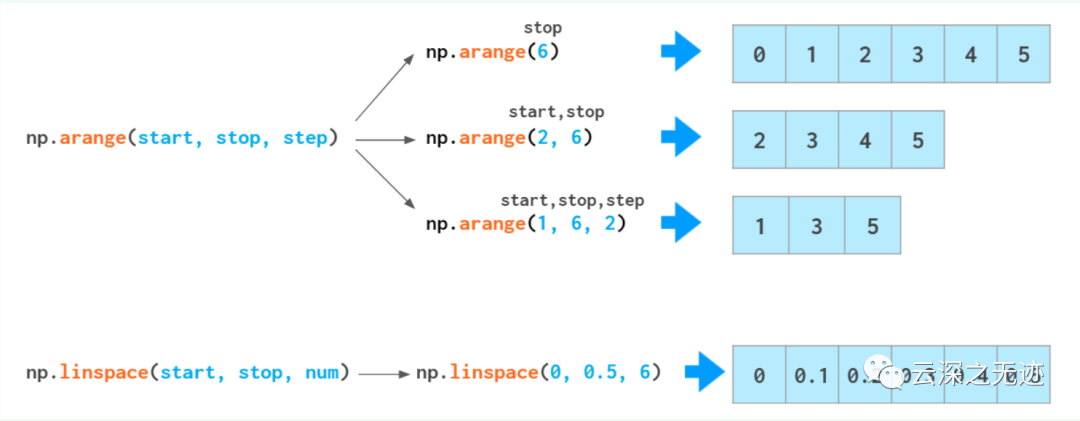
可以使用單調(diào)序列初始化數(shù)組

arange對浮點不太友好

隨機數(shù)組也可以生成，這個太常見了

生成完成了，下一個階段就是取數(shù)了;

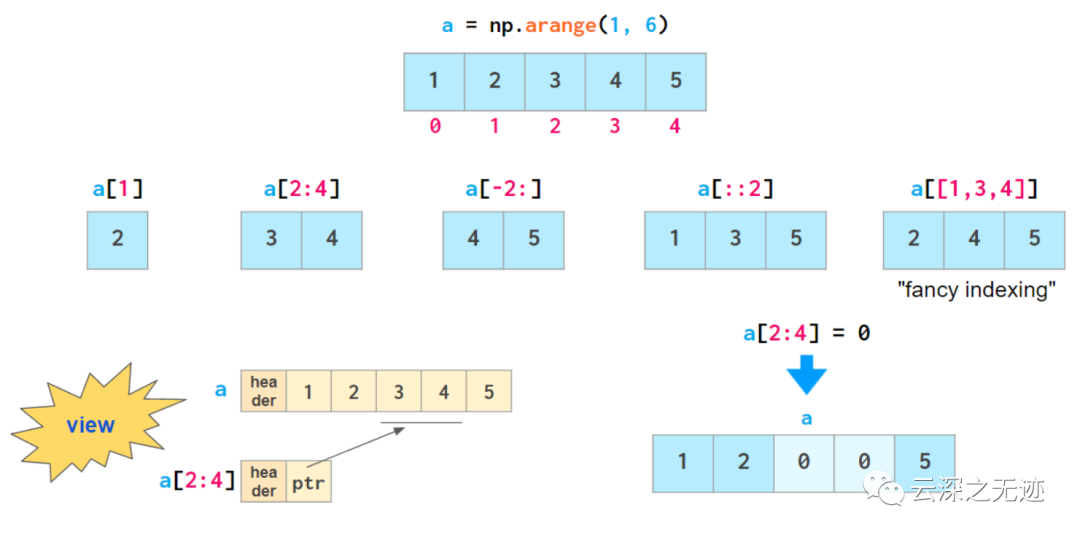
就像這樣，通過索引來切割

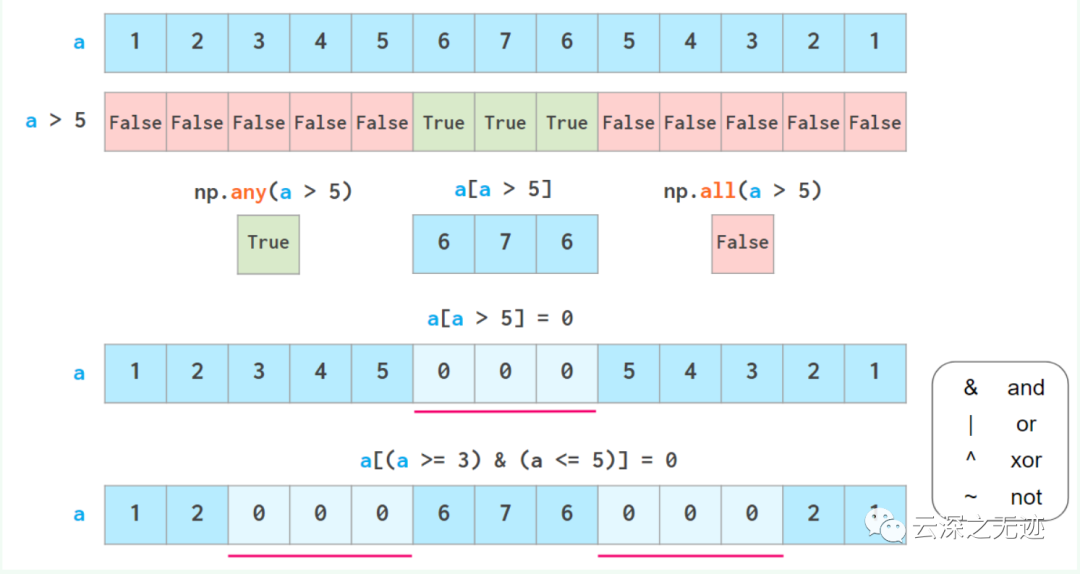
布爾和掩碼真的是太好用了！！！！

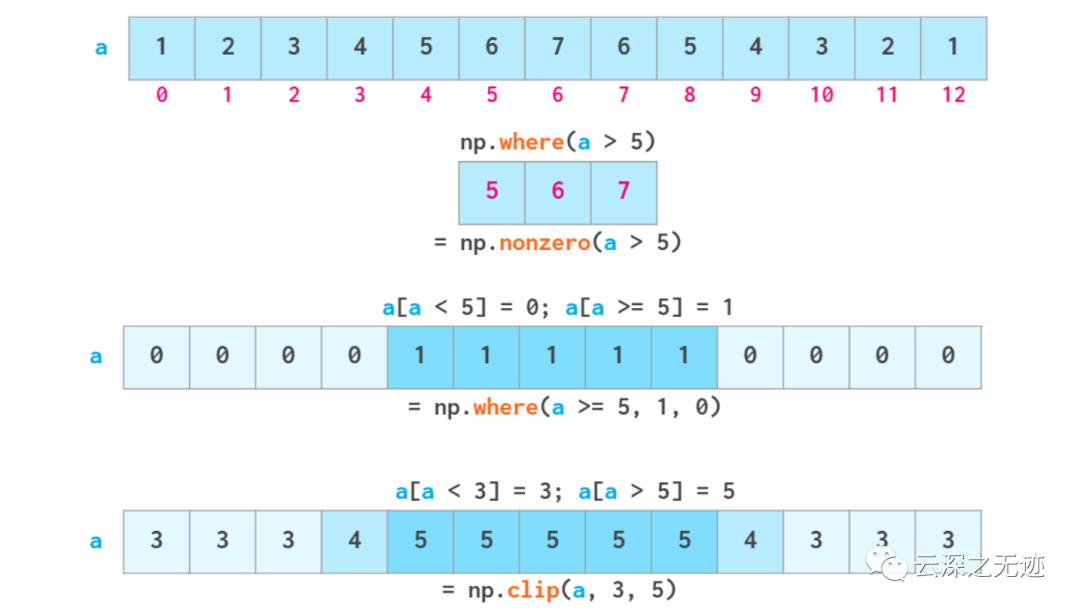
還有專有的函數(shù)，大規(guī)模的進行取數(shù)操作

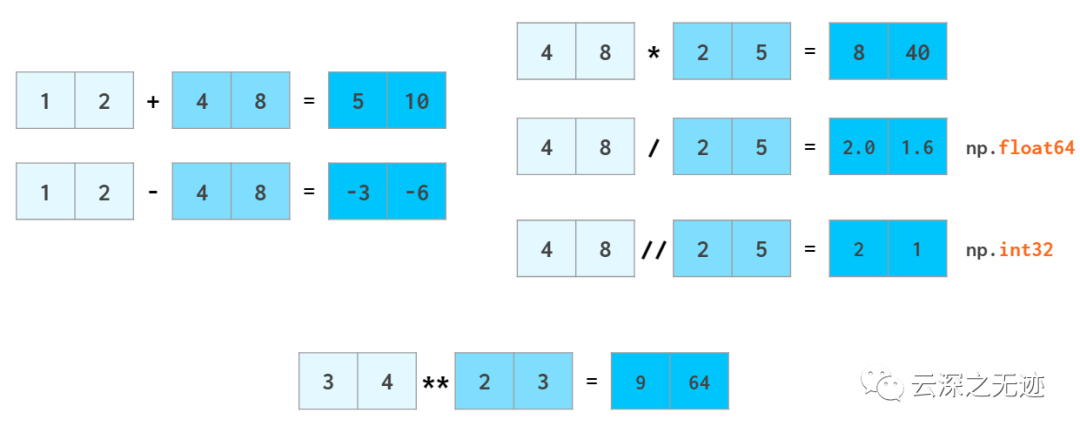
向量化操作無疑是最引人注目的東西

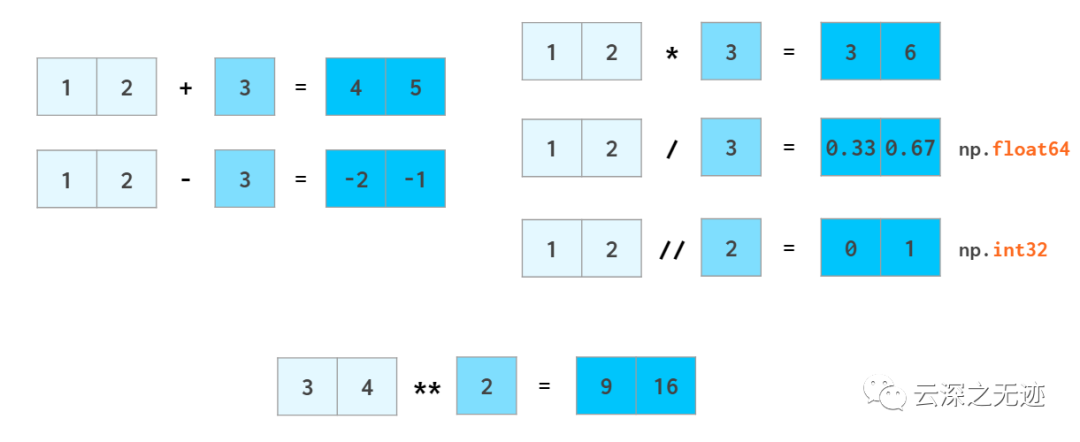
浮點也OJBK

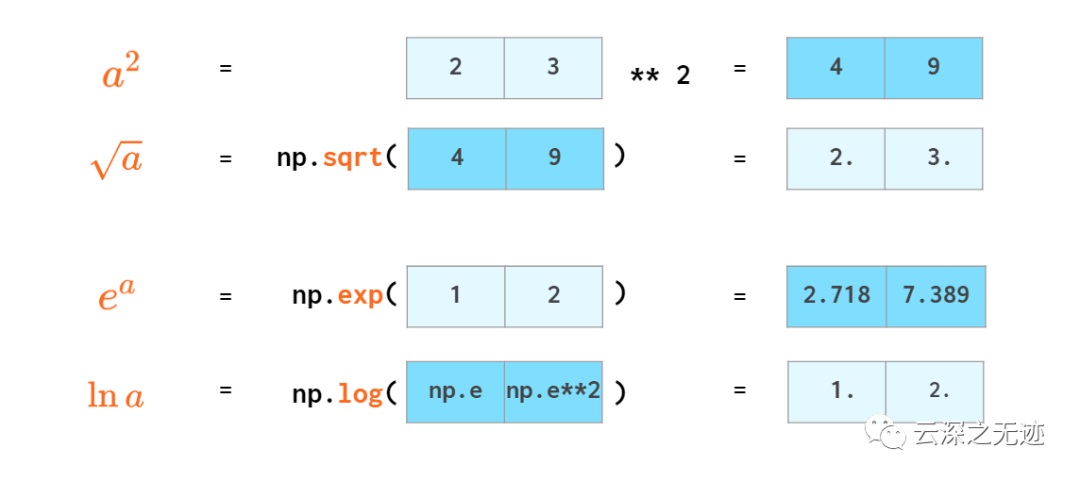
常見函數(shù)不在話下，矢量化的意義在于可以同時操作海量數(shù)據(jù)，具有天然的并行化。

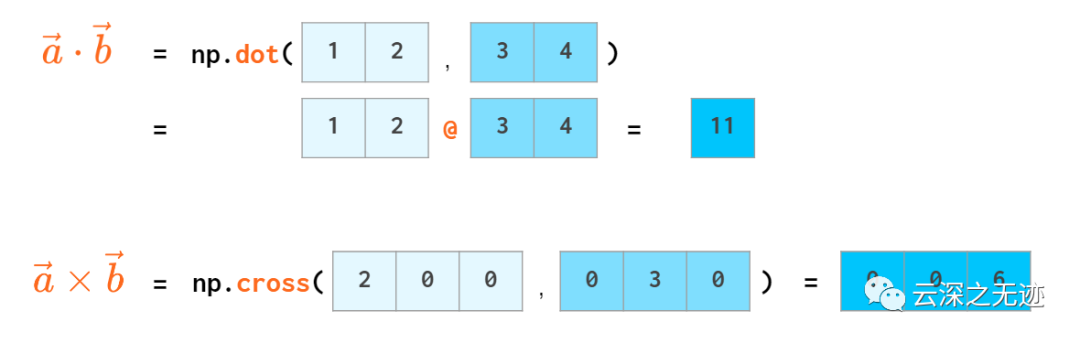
這是內(nèi)積和叉積

三角函數(shù)不能少

四舍五入的操作也有

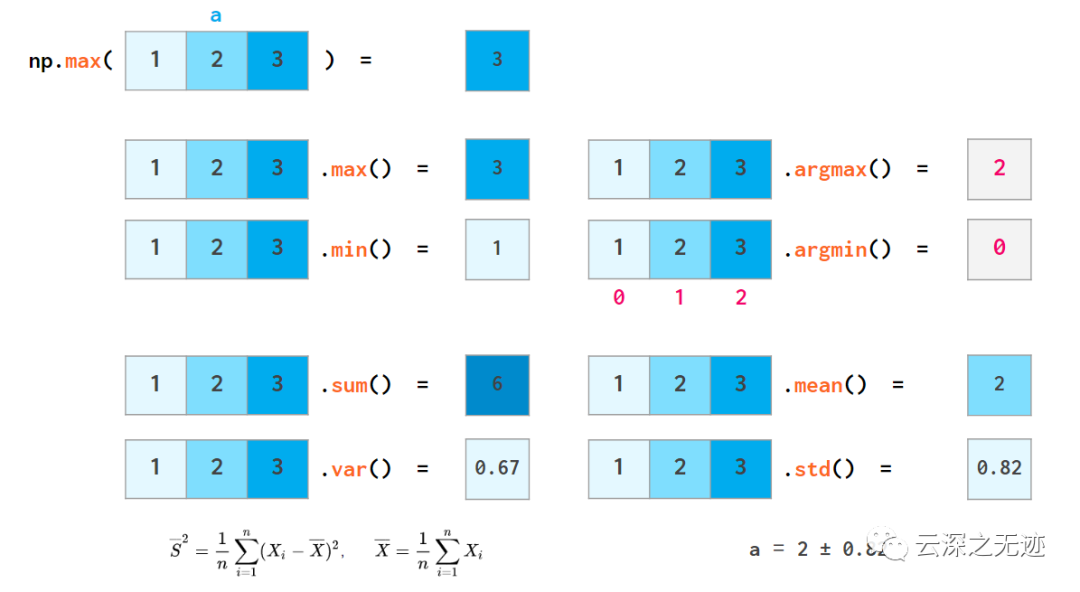
關(guān)于統(tǒng)計的功能也有

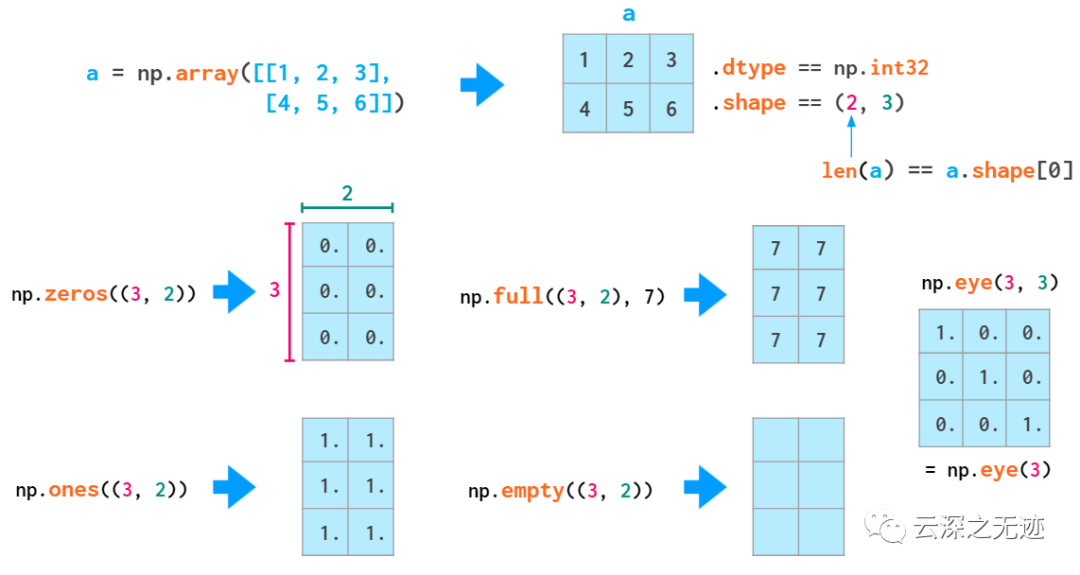
矩陣的初始化，注意參數(shù)的位置，先行，后列

隨機矩陣也是經(jīng)常要用的

索引語法要好好的看，注意是從0開始，記得+1

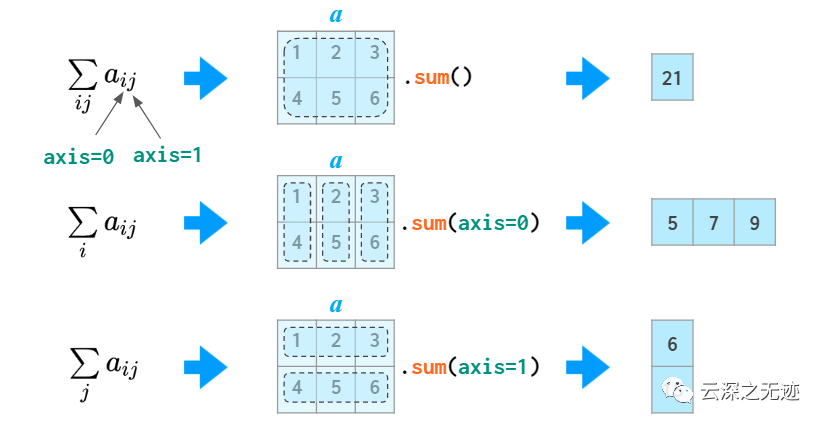
上面放過這個圖，但是為了完整性，這里再放一次

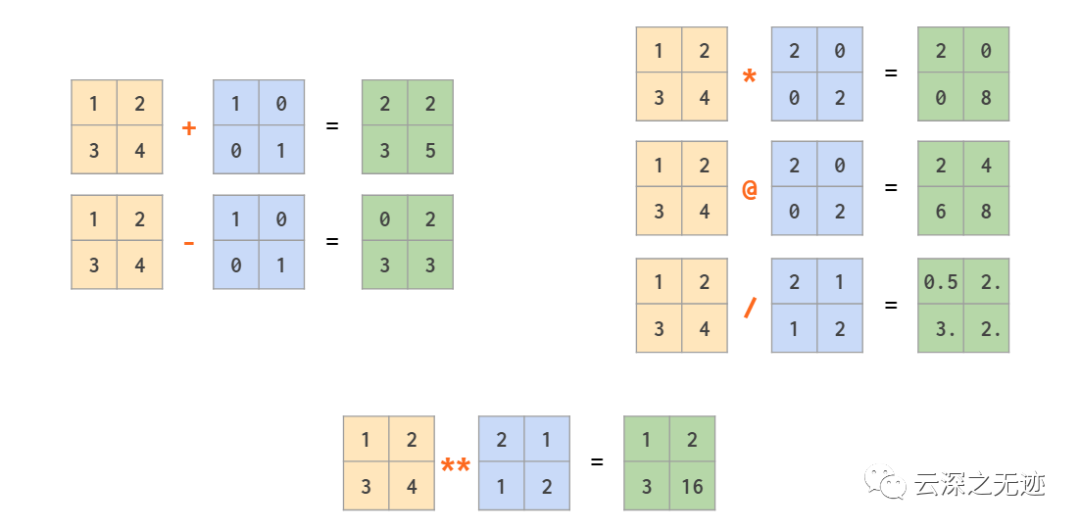
@計算矩陣的乘積

廣播機制，這個怎么說呢。就是運算我們一般是規(guī)模相同的進行計算，不相同的時候需要變的相同。其實就是一套規(guī)則。

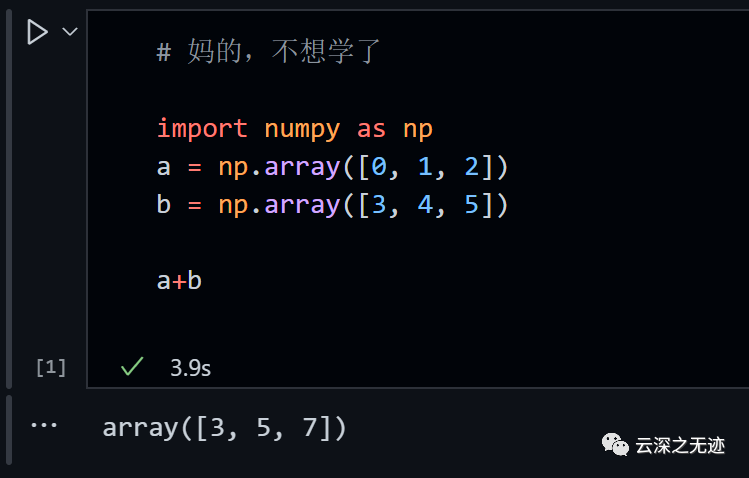
先簡單點，規(guī)模一樣

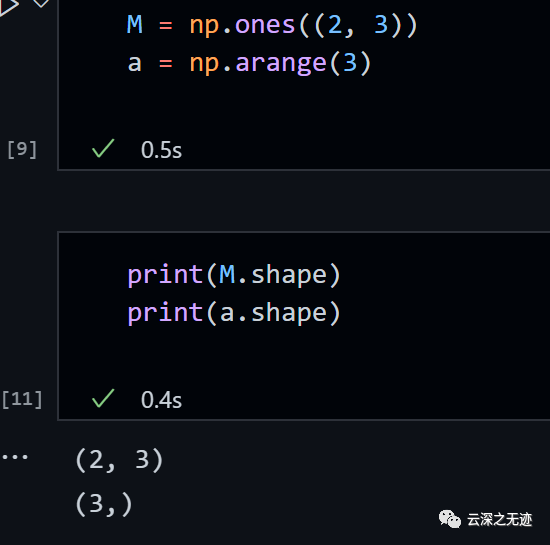
這個就不一樣了

這就是廣播，先是維數(shù)的調(diào)整，兩個維數(shù)一致，接著調(diào)整內(nèi)部的參數(shù)

你看這個，9x9與后面這樣的東西運算，不就是要使用廣播嗎？

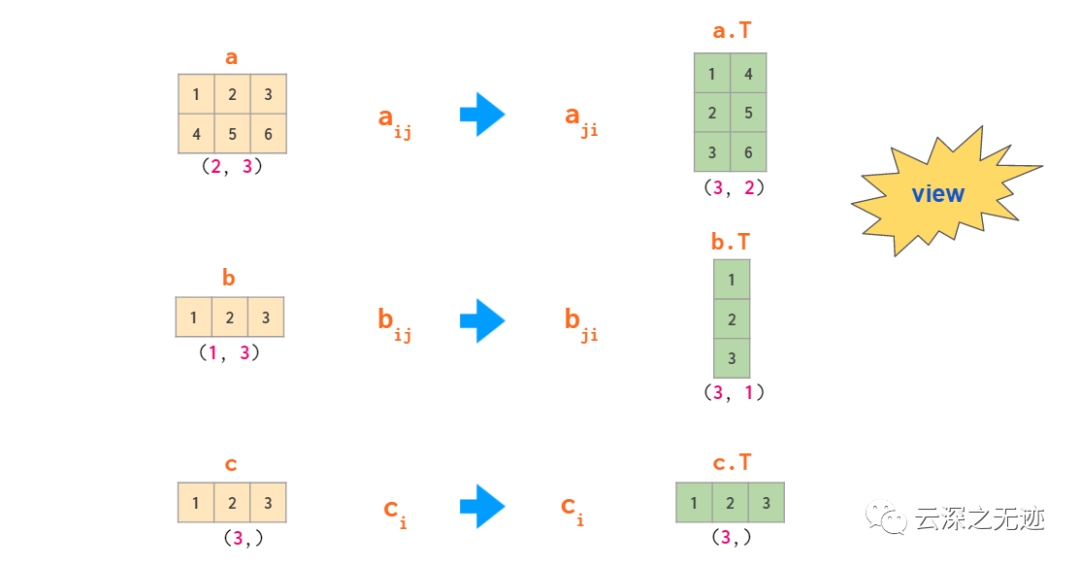
轉(zhuǎn)置

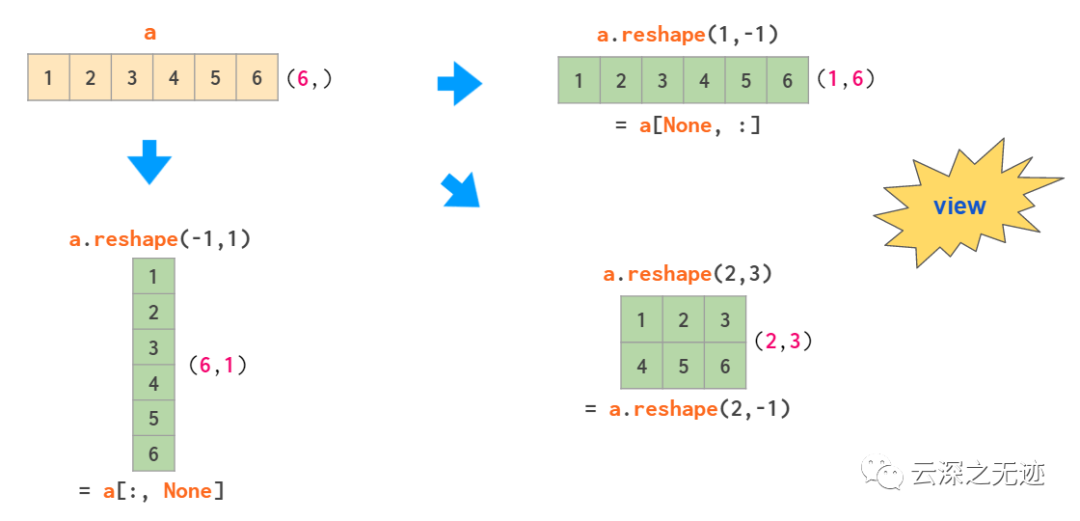
數(shù)組重構(gòu)

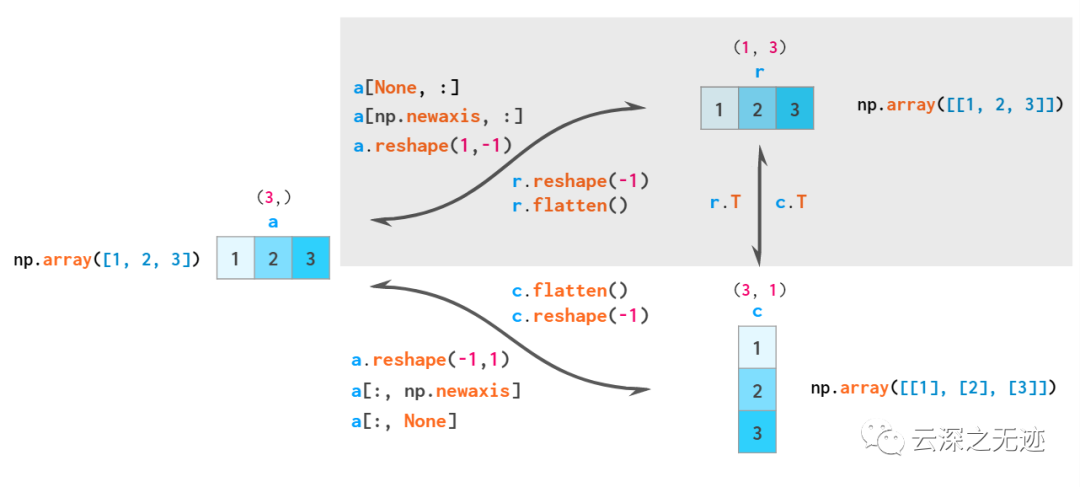
互相之間的轉(zhuǎn)換圖，這個要記住

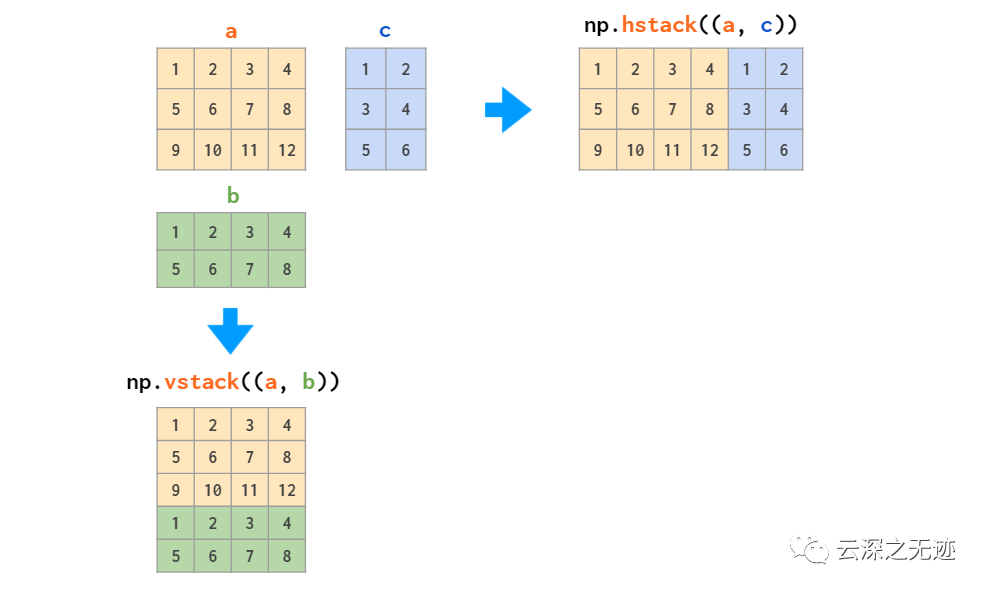
拼接操作，我也寫過

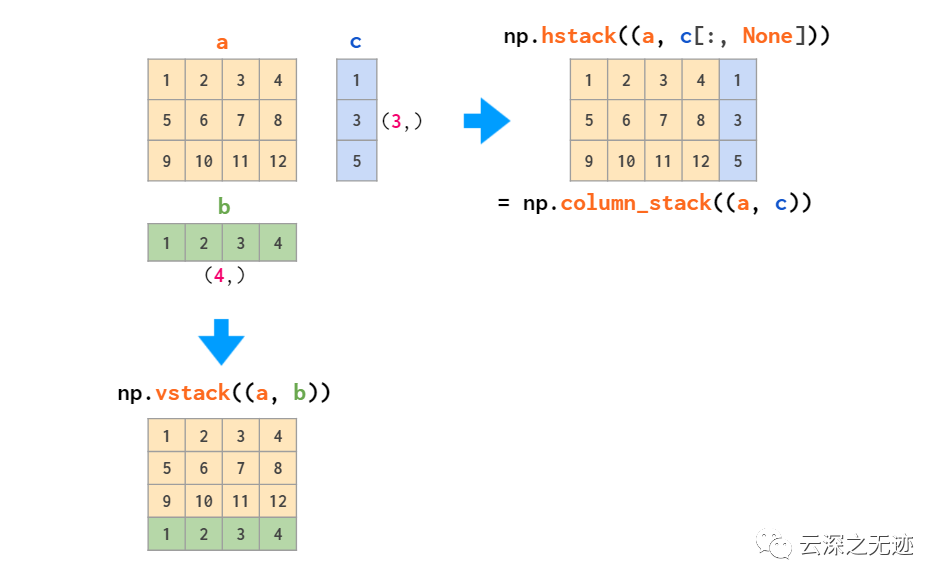
也是拼接

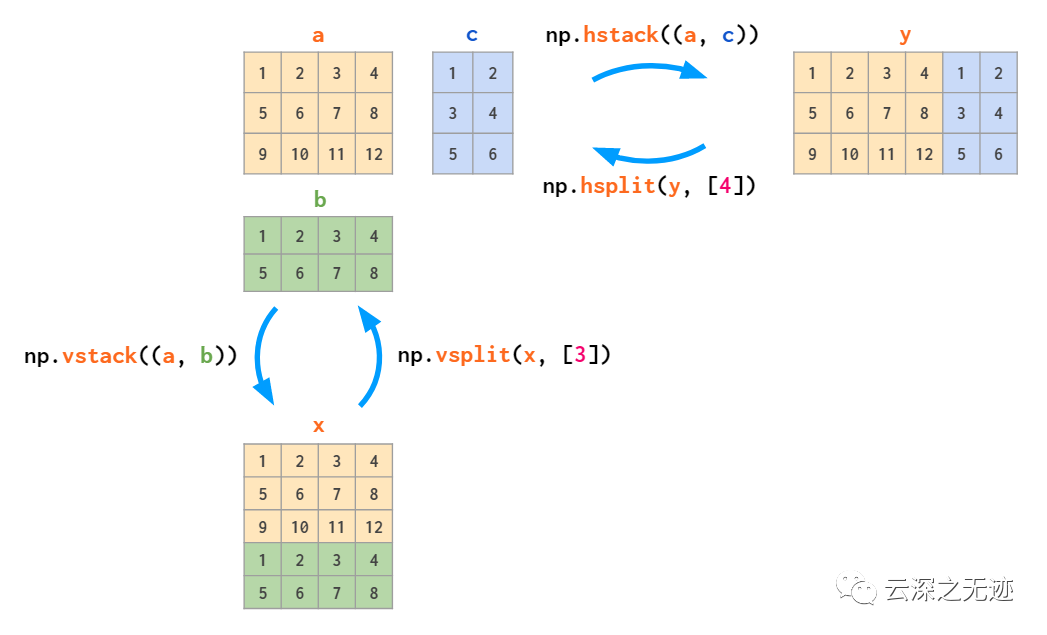
拆分

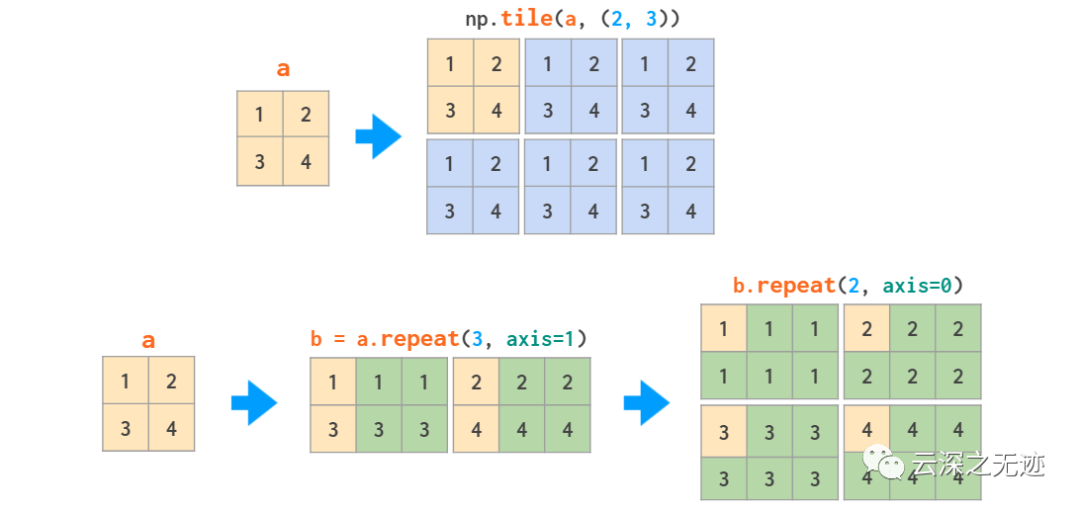
tile復(fù)雜黏貼，repeat是分頁打印

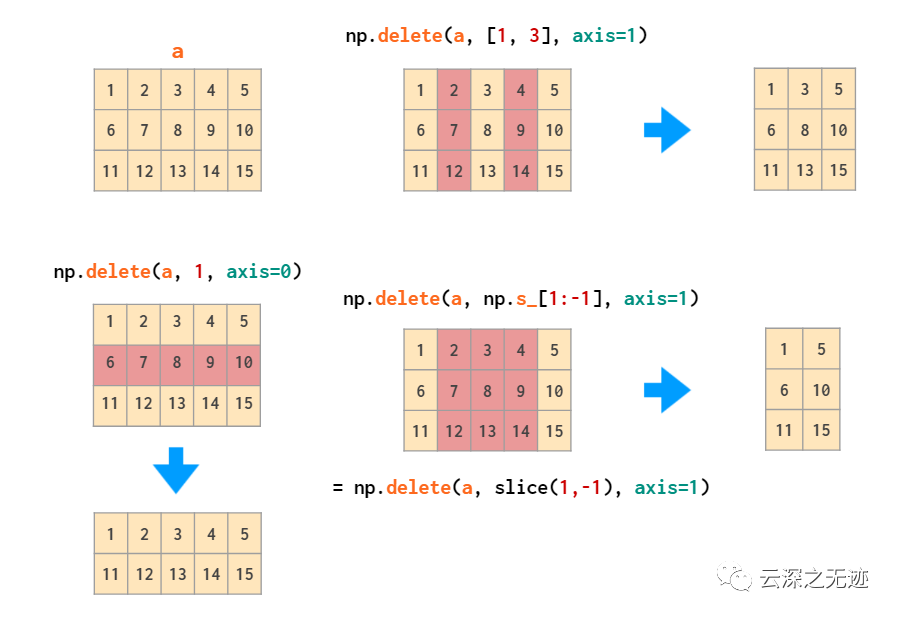
這個是可以刪除對應(yīng)的行列，這不就是白給

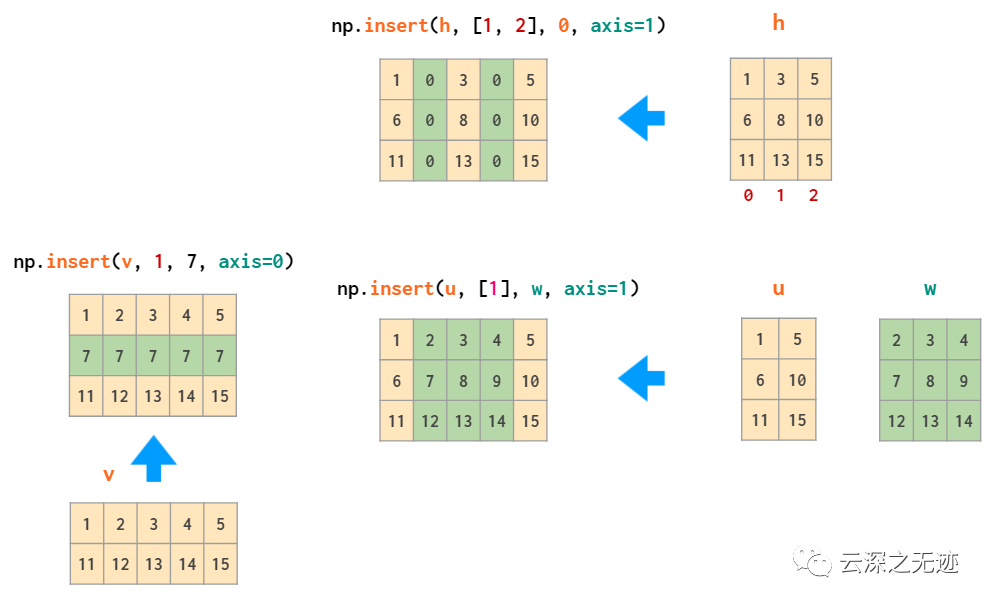
插入操作

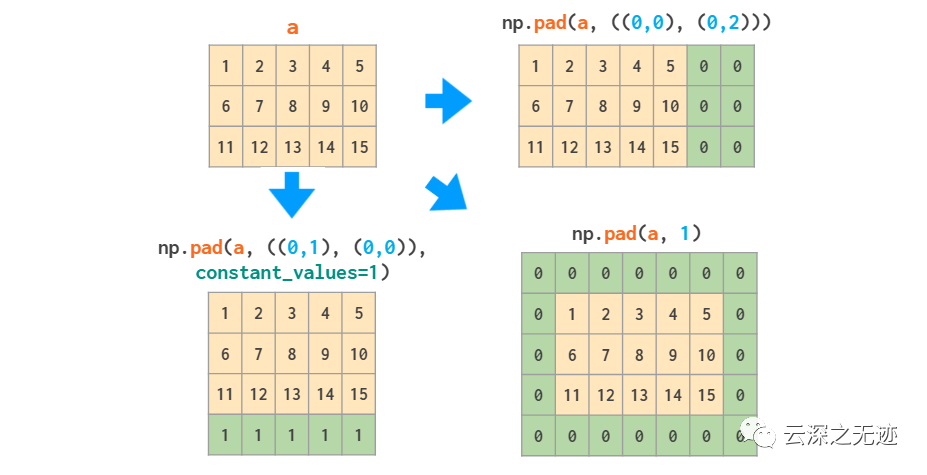
邊界添加常數(shù)，就好像鑲邊一樣

下面的內(nèi)容有趣:

創(chuàng)建這樣的東西，C和Python的做法是這樣的

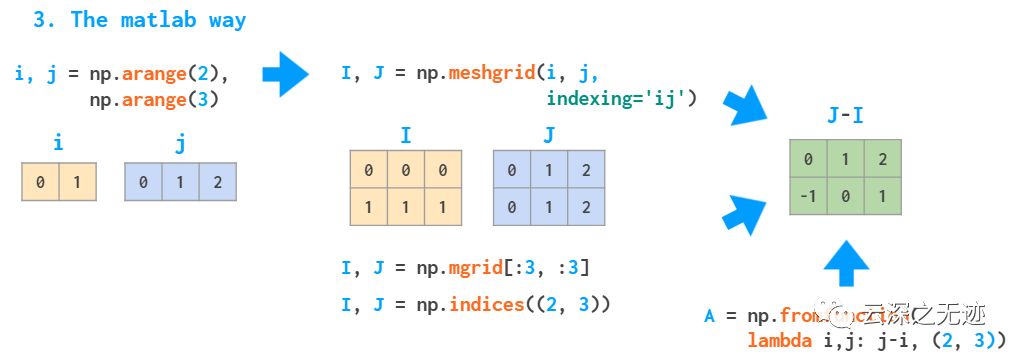
matlab這樣做，相對于先生成兩個行向量，接著開始廣播，運算

這個地方是numpy的做法，效率更高。上面是生成網(wǎng)格的算法

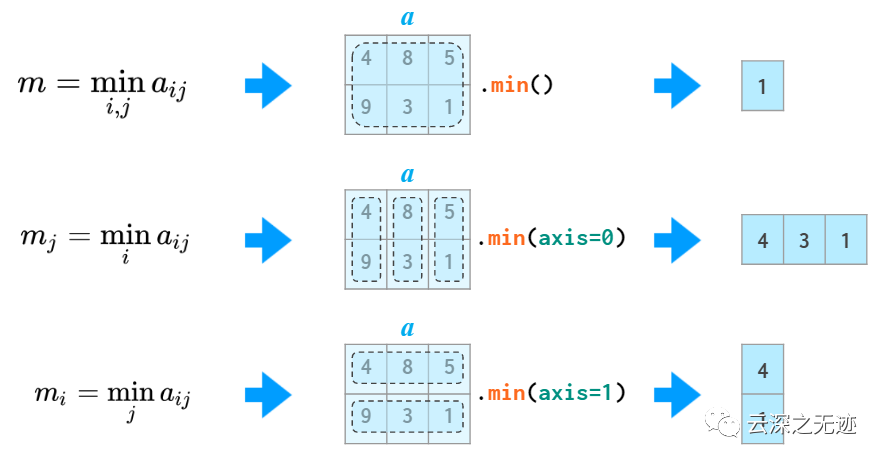
numpy的排序算法有點問題，這里就不討論了，因為我也沒有搞明白

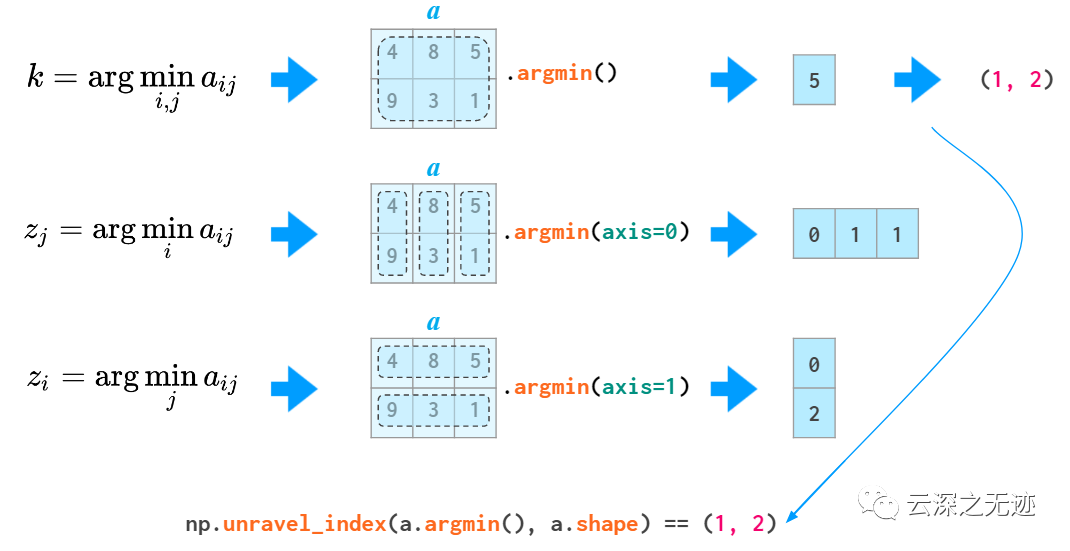
返回索引，其實就是坐標，有時位置是很重要的

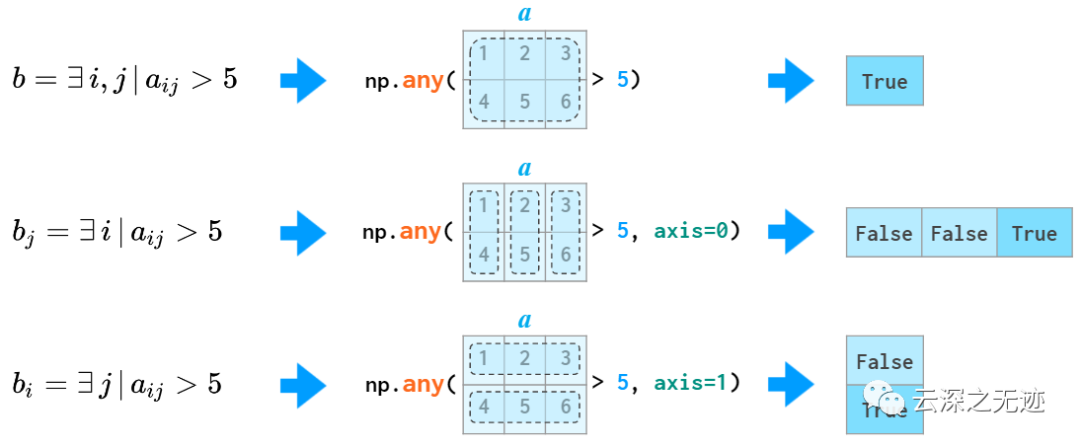
all和any就是有沒有的問題

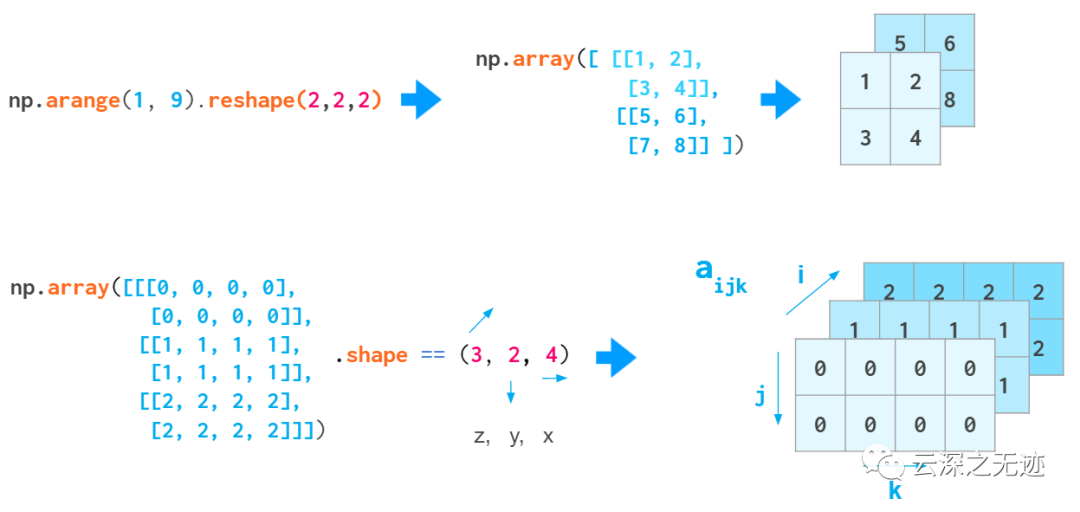
三維的接下來會說

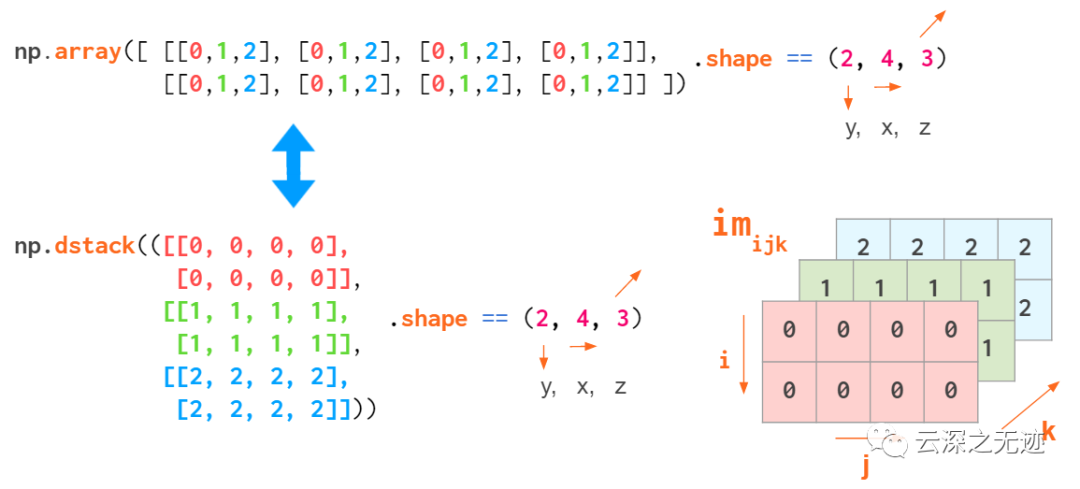
至于形狀怎么樣，會看你的約定。

接下來再加點東西，也不知道有沒有人能看到這里。

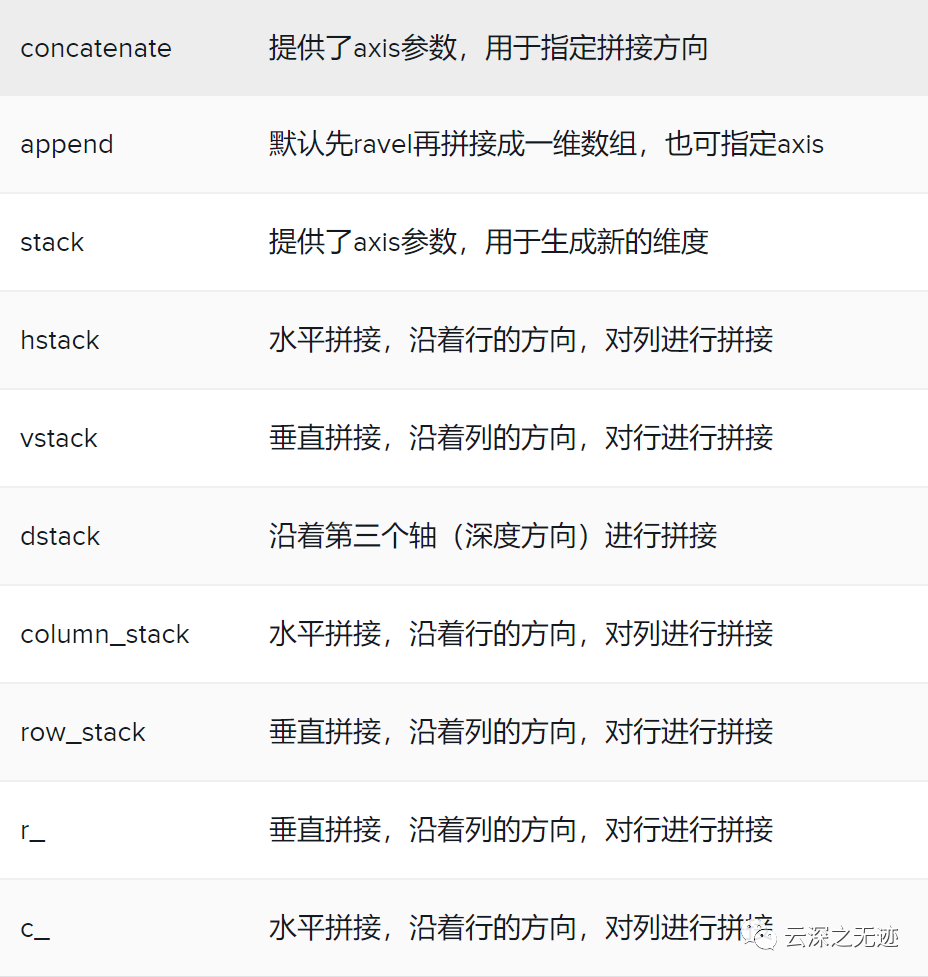
上面頻繁的說了拼接的事情，這里帶你看看有什么參數(shù)

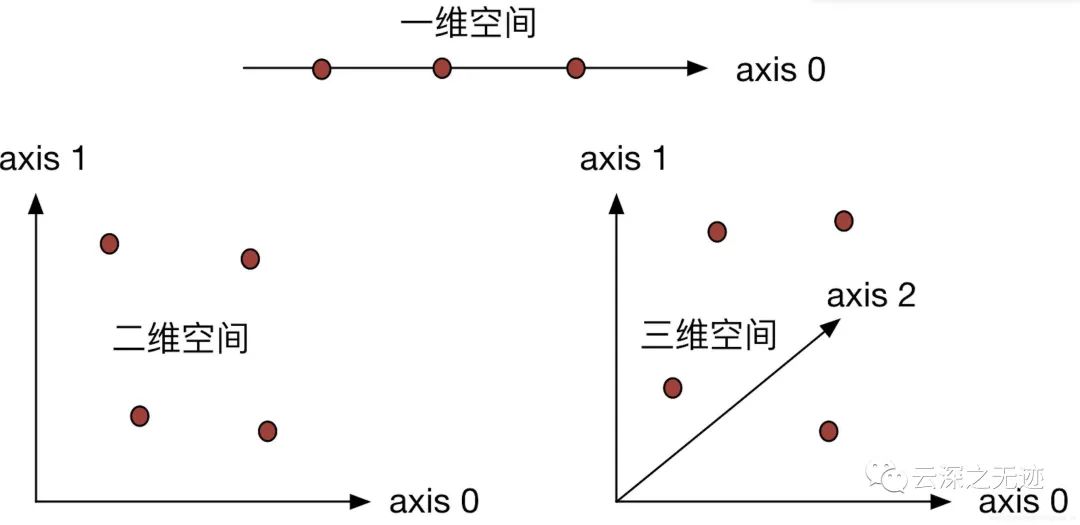
這個圖沒什么用，我就是覺得好看

審核編輯 ：李倩