一、寫(xiě)在文前

在實(shí)際工作中經(jīng)常會(huì)遇到類(lèi)似概率分布的問(wèn)題。概率問(wèn)題經(jīng)常會(huì)涉及到隨機(jī)數(shù)分布問(wèn)題，過(guò)冷水就遇到了如何生成滿(mǎn)足如下分布數(shù)據(jù)的問(wèn)題。

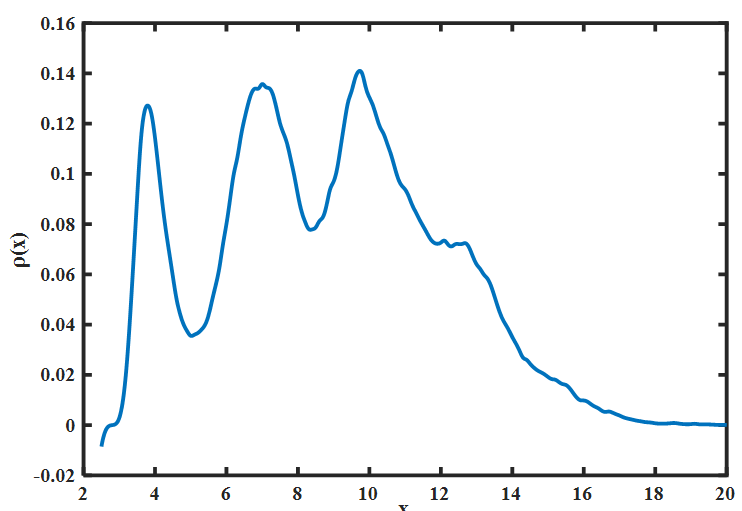
數(shù)據(jù)范圍在2~20之間，但是生成的數(shù)據(jù)要滿(mǎn)足如圖所示的概率密度函數(shù)，在一般問(wèn)題中我們經(jīng)常遇到的生成平均數(shù)據(jù)使用rand()函數(shù)就可以生成0~1區(qū)間的隨機(jī)數(shù)據(jù)然后對(duì)數(shù)據(jù)進(jìn)行處理就可以得到滿(mǎn)足任意區(qū)間的數(shù)據(jù),生成滿(mǎn)足正態(tài)分布的隨機(jī)也有現(xiàn)成函數(shù)randn()函數(shù)可調(diào)用，如圖所示的問(wèn)題 how do?,本期過(guò)冷水就詳細(xì)的給大家講一講如何Matlab生成滿(mǎn)足任意概率密度的分布函數(shù)。二、均勻分布matlab的rand指令可以幫助我們生成0-1均勻分布的數(shù)據(jù)，這樣，如果我們想要[a,b]的分布數(shù)據(jù)，只需要a+(b-a)*rand就可以。需要注意的是rand函數(shù)有其內(nèi)置的平均值和標(biāo)準(zhǔn)差

A=rand(1000000,1);muA=mean(A)sigmaA = std(A)muA =0.5000sigmaA =0.2887

如果想要生成指定均值和方差的隨機(jī)數(shù)該如何實(shí)現(xiàn)？其實(shí)在已知均勻分布的期望和方差條件下是可以反求均勻分布的區(qū)間的。均勻分布的期望和方差和隨機(jī)數(shù)區(qū)間存在以下關(guān)系

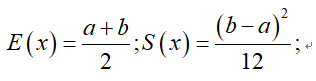
如果想生成均值E=0;S=1的隨機(jī)數(shù),可以利用上述公式反推出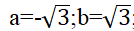

B=2*sqrt(3)*rand(10000000,1)-sqrt(3);muB=mean(B)sigmaB = std(B)muB =3.8898e-04sigmaB =1.0000

均值和方差滿(mǎn)足預(yù)期，掌握了均勻分?jǐn)?shù)數(shù)據(jù)生成后，可以做生成在約束條件的下均勻分布，在二維空間繪制半徑為r的圓內(nèi)均勻分布數(shù)據(jù)點(diǎn)

figure1 = figure;blackboard=imread('E:Picturelackboard.jpg'); colormap(gray);axes1 =axes('Parent',figure1,'units','normalized','position',[0 0 1 1]);uistack(axes1,'down')image(blackboard,'Parent',axes1,'CDataMapping','scaled')set(axes1,'handlevisibility','off','visible','off');axes2 = axes('Parent',figure1);hold(axes2,'on');plot(x,y,'MarkerFaceColor',[1 00],'Marker','o','LineStyle','none','Color',[1 0 0]);box(axes2,'on');axis(axes2,'equal');axis(axes2,'off');hold(axes2,'off');set(axes2,'FontName','Times NewRoman','FontSize',12,'FontWeight','bold','LineWidth',3,'Color','none');set(axes2,'Color','none','LineWidth',6,'TickLength',[0.010.005],'XColor',[1 0 1],'YColor',[1 0 1],'ZColor',[1 0 1]);同理可繪制半徑為r的三維球內(nèi)均勻分布數(shù)據(jù)點(diǎn)angle1=rand(1,1000)*2*pi;angle2=acos(rand(1,1000)*2-1);r=power(rand(1,1000),1/3);x=r.*cos(angle1).*sin(angle2);y=r.*sin(angle1).*sin(angle2);z=r.*cos(angle2); figure1 = figure;colormap(gray);axes1 = axes('Parent',figure1,'units','normalized','position',[00 1 1]);uistack(axes1,'down')image(blackboard,'Parent',axes1,'CDataMapping','scaled')set(axes1,'handlevisibility','off','visible','off');axes2 = axes('Parent',figure1); hold(axes2,'on');plot3(x,y,z,'MarkerFaceColor',[10 0],'Marker','o','LineStyle','none','Color',[1 0 0]);view( axes2,[15 30])box(axes2,'on');axis(axes2,'square');hold(axes2,'off');box(axes2,'on')set(axes2,'Color','none','LineWidth',6,'TickLength',[0.010.005],'XColor',[1 0 1],'YColor',[1 0 1],'ZColor',[1 0 1]);

Interesting!在指定范圍生成數(shù)據(jù)是非常實(shí)用的技能，其實(shí)如果能夠構(gòu)造出合適的約束條件,圖形將會(huì)更加多樣化。

三、正態(tài)分布

上述案例是給出了約束條件下的均勻分布，那么如何給出在約束條件下的非均勻分布？正態(tài)分布是非均勻分布中具有代表性的案例，正態(tài)分布實(shí)際可以直接調(diào)用randn()函數(shù)，為了比較清楚看正態(tài)分布生成隨機(jī)數(shù)的特點(diǎn)，

我們以二維空間球體為案例來(lái)看一下正態(tài)分布數(shù)據(jù)。

angle=rand(1,1000)*2*pi;%(0,2*pi)之間均勻分布數(shù)據(jù)點(diǎn)r=sqrt(normrnd(0.3,0.13,[1,1000]));%(0,1)之間r^2均勻分布數(shù)據(jù)點(diǎn)x=r.*cos(angle);y=r.*sin(angle);figure1 = figure;axes1 = axes('Parent',figure1);hold(axes1,'on');plot(x,y,'MarkerFaceColor',[1 00],'Marker','o','LineStyle','none','Color',[1 0 0]);box(axes1,'on');axis(axes1,'square');hold(axes1,'off');set(axes1,'FontName','Times NewRoman','FontSize',12,'FontWeight','bold','LineWidth',3);

從圖像上我們生成了一圓層厚度不一致的隨機(jī)數(shù),已經(jīng)實(shí)現(xiàn)了滿(mǎn)足約束條件下的非隨機(jī)分布只要在往前走一步看如何生成特地的非隨機(jī)分布

四、任意隨機(jī)分布數(shù)據(jù)生成

可以采用MonteCarlo 方法采用隨機(jī)約束的方法來(lái)生成隨機(jī)數(shù)。

1:選定生成數(shù)據(jù)范圍[a，b]，并在此范圍生成服從均勻分布數(shù)據(jù)xi；

2:生成服從均勻分布的數(shù)據(jù)y.y的取值范圍為概率密度分布范圍；

3：若y < f ( x )保留x,否則舍去。保留的x即為生成的數(shù)據(jù),否則舍去。這一步就是對(duì)利用Y值對(duì)x進(jìn)行甄選

我們來(lái)實(shí)踐一下

fun=@(x)(0.2089.*exp(-((x-9.985)./0.7535).^2)+ 0.*exp(-((x+1.593)./0.0846).^2)+0.1223.*exp(-((x-3.874)./0.585).^2)-0.1669.*exp(-((x+0.1669)./0.6609).^2)-0.02173.*exp(-((x-9.238)./0.5248).^2)-0.09805.*exp(-((x-8.219)./0.9768).^2)+0.1764.*exp(-((x-7.735)./1.995).^2) +0.07335.*exp(-((x-11.83)./2.733).^2))xmin=2.6;xmax=20;num=2000; %數(shù)據(jù)數(shù)量n=1;data1=zeros(1,num);whilen

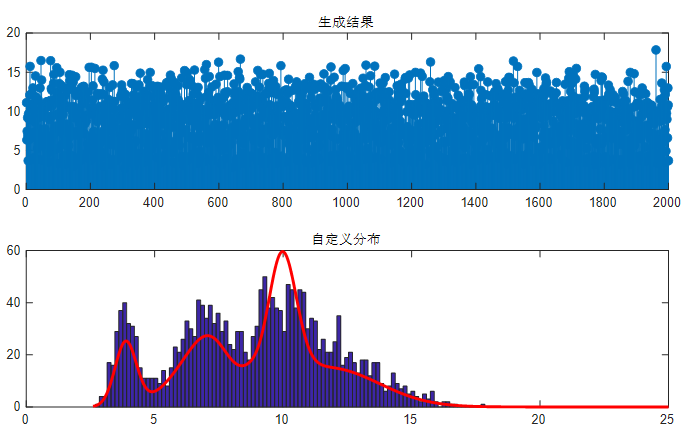
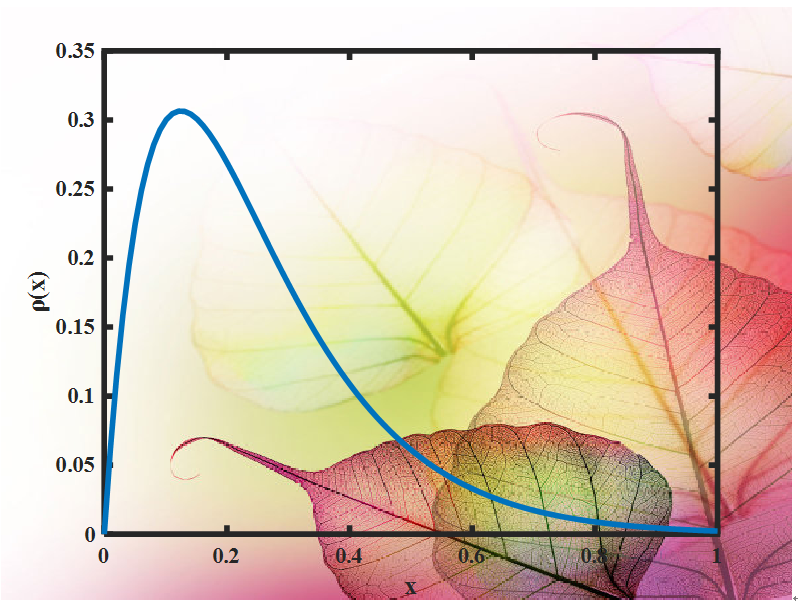
根據(jù)上文思路寫(xiě)出的代碼生成數(shù)據(jù)基本滿(mǎn)足一開(kāi)始的分布特征，這樣就實(shí)現(xiàn)了自定義分布數(shù)據(jù)。可以利用自定義函數(shù)生成數(shù)據(jù)點(diǎn)特殊的分布函數(shù)，我們給出如下分布特征的密度函數(shù)

x=linspace(0,1,100);y =(2*x/0.3).*exp(-4*x/0.5);figureplot(x,y)figure1 = figure;axes1 = axes('Parent',figure1);hold(axes1,'on');plot(x,y,'LineWidth',3);ylabel('ρ(x)');xlabel('x');box(axes1,'on');hold(axes1,'off');set(axes1,'FontName','Times New Roman','FontSize',12,'FontWeight','bold','LineWidth',3);

將這樣的一個(gè)分布應(yīng)用在二維圓的繪制上

fun=@(x)(2*x/0.3).*exp(-4*x/0.5);xmin=0;xmax=1;num=2000; %數(shù)據(jù)數(shù)量n=1;data1=zeros(1,num);while n

我們得到和正態(tài)分布約束條件下的圖像有相反的分布趨勢(shì)，中間數(shù)據(jù)密集靠近外環(huán)的數(shù)據(jù)點(diǎn)較少，這樣的一種分布在實(shí)際情況中就是有點(diǎn)像密度的非均勻變化，我們我們將生成的數(shù)據(jù)賦予其物理意義，就成功的將統(tǒng)計(jì)統(tǒng)計(jì)上的非均勻分布實(shí)實(shí)在在用在表述物質(zhì)性質(zhì)變化上了。很有實(shí)際意義。有需要的讀者可自主嘗試應(yīng)用，本期過(guò)冷水就給大家分享上述內(nèi)容。

審核編輯 ：李倩