首先我們先來簡單了解一下什么是數(shù)字圖像處理(Digital Image Processing),先看一下數(shù)字圖像主要的兩個(gè)應(yīng)用領(lǐng)域:
1.改善圖示信息以便人們解釋;
2.為存儲(chǔ)、傳輸和表示而對圖像數(shù)據(jù)進(jìn)行處理,以便于機(jī)器自動(dòng)理解
我們可以簡單理解為就將一幅原始圖像,使用計(jì)算機(jī)處理為更為我們所能理解或所需要的形式,如圖1-1所示,為基于邊緣檢測的免疫細(xì)胞圖像自動(dòng)分割過程示意圖
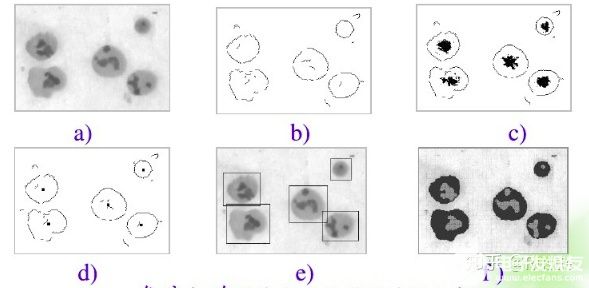
圖 1-1 克隆細(xì)胞圖像自動(dòng)分割過程示意圖
讓我們再看一個(gè)例子,如圖1-2 ,為經(jīng)典的車牌檢測算法,將原始圖像進(jìn)行灰度圖轉(zhuǎn)換、邊緣檢測、形態(tài)學(xué)腐蝕膨脹等操作,得到車牌區(qū)域,隨后將車牌區(qū)域進(jìn)行切割(這個(gè)是筆者剛?cè)腴T時(shí)做的小demo,還沒有用到深度學(xué)習(xí)模型,用的是knn,因此識(shí)別結(jié)果很差,各位看官會(huì)心一笑就好了哈)
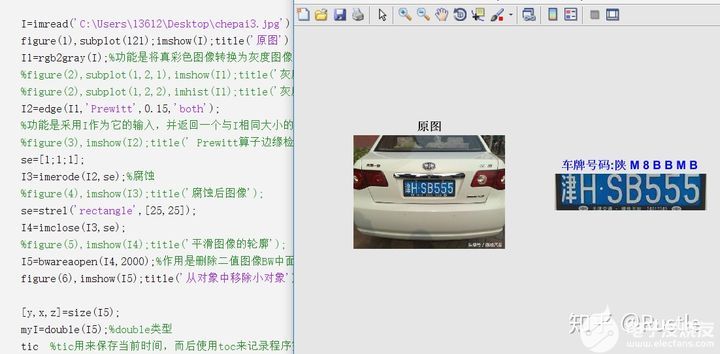
圖2 -2 車牌檢測
OK,在我們大致了解了數(shù)字圖像處理之后,接下來介紹數(shù)字圖像處理一些基本的算法。
二.數(shù)字圖像處理基礎(chǔ)知識(shí)與算法
接下來先簡單介紹一下一些學(xué)習(xí)數(shù)字圖像處理的基礎(chǔ)知識(shí)與算法
1).數(shù)字圖像
數(shù)字圖像指的是現(xiàn)在的圖像都是以二維數(shù)字表示,每個(gè)像素的灰度值均由一個(gè)數(shù)字表示,范圍為0-255(2^8)
2).二值圖像、灰度圖像、彩色圖像
二值圖像(Binary Image):圖像中每個(gè)像素的灰度值僅可取0或1,即不是取黑,就是取白,二值圖像可理解為黑白圖像
灰度圖像(Gray Scale Image):圖像中每個(gè)像素可以由0-255的灰度值表示,具體表現(xiàn)為從全黑到全白中間有255個(gè)介于中間的灰色值可以取
彩色圖像(Color Image):每幅圖像是由三幅灰度圖像組合而成,依次表示紅綠藍(lán)三通道的灰度值,即我們熟知的RGB,此時(shí)彩色圖像要視為三維的[height,width, 3]
下面用一張圖來感受一下灰度圖與彩色圖像之間的聯(lián)系與差別

圖2 -1 RGB圖像的分解
其中還有一個(gè)很重要的公式,即彩色圖像轉(zhuǎn)為灰度圖的計(jì)算公式:
G
Gray表示灰度圖像,RGB則表示彩色圖像的紅(red)、綠(green)、藍(lán)(blue)三通道灰度值
3).鄰接性、連通性
4鄰域:假設(shè)有一點(diǎn)像素p坐標(biāo)為(x, y),則它的4領(lǐng)域是(x + 1, y), (x - 1, y), (x, y + 1), (x, y - 1)
D鄰域:假設(shè)有一點(diǎn)像素p坐標(biāo)為(x, y), 則它的D領(lǐng)域是(x + 1, y + 1), ( x + 1, y - 1), (x - 1, y + 1)
(x - 1, y - 1)
8鄰域:將4領(lǐng)域與D領(lǐng)域的集合取并集,即表示為8鄰域
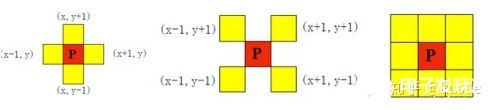
圖2 - 2 4鄰域(左)、 D鄰域(中)、 8鄰域(右)
4連通:對于在像素點(diǎn)p的4鄰域內(nèi)的像素均與像素點(diǎn)p形成4連通
8連通:對于在像素點(diǎn)p的8鄰域內(nèi)的像素均與像素點(diǎn)p形成8連通
4).濾波
濾波的目的主要兩個(gè):
1.通過濾波來提取圖像特征,簡化圖像所帶的信息作為后續(xù)其它的圖像處理
2.為適應(yīng)圖像處理的需求,通過濾波消除圖像數(shù)字化時(shí)所混入的噪聲
其中第一點(diǎn)就是邊緣檢測中所使用的基本思想,即簡化圖像信息,使用邊緣線代表圖像所攜帶信息
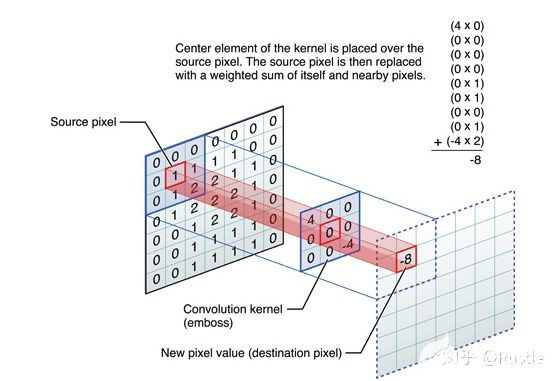
濾波可理解為濾波器(通常為3*3、5*5矩陣)在圖像上進(jìn)行從上到下,從左到右的遍歷,計(jì)算濾波器與對應(yīng)像素的值并根據(jù)濾波目的進(jìn)行數(shù)值計(jì)算返回值到當(dāng)前像素點(diǎn),如圖 2-3所示,藍(lán)色塊表示濾波器,對圖像進(jìn)行點(diǎn)積運(yùn)算并賦值到圖像
具體公式表示為:
(其中
表示當(dāng)前像素點(diǎn),
表示當(dāng)前像素與濾波器對應(yīng)值相乘的值,n為濾波器大小,舉例來說如若此濾波器值全為1,則此公式計(jì)算的是當(dāng)前像素點(diǎn)的8連通像素點(diǎn)的平均值,因此濾波完后的圖像應(yīng)表現(xiàn)為模糊的效果,模糊程度取決于濾波器的大小,濾波器大小(size)越大,模糊效果越明顯)
三.邊緣檢測(Sobel、Prewitt、Roberts、Canny、Marr-Hildreth)
1.基本邊緣檢測算子
在介紹完濾波的知識(shí)后,學(xué)習(xí)基本邊緣檢測算法是一件很輕松的事情,因?yàn)檫吘墮z測本質(zhì)上就是一種濾波算法,區(qū)別在于濾波器的選擇,濾波的規(guī)則是完全一致的
為了更好理解邊緣檢測算子,我們引入梯度(gradient)這一概念,梯度是人工智能(artificial intelligence)非常重要的一個(gè)概念,遍布機(jī)器學(xué)習(xí)、深度學(xué)習(xí)領(lǐng)域,學(xué)過微積分的同學(xué)應(yīng)該知道一維函數(shù)的一階微分基本定義為:
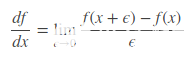
而我們剛才也提到了,圖像的濾波一般是基于灰度圖進(jìn)行的,因此圖像此時(shí)是二維的,因此我們在看一下二維函數(shù)的微分,即偏微分方程:
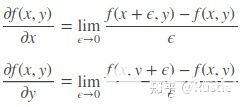
由上面的公式我們可以看到,圖像梯度即當(dāng)前所在像素點(diǎn)對于X軸、Y軸的偏導(dǎo)數(shù),所以梯度在圖像處理領(lǐng)域我們可以也理解為像素灰度值變化的速度,下面我們舉一個(gè)簡單的例子:
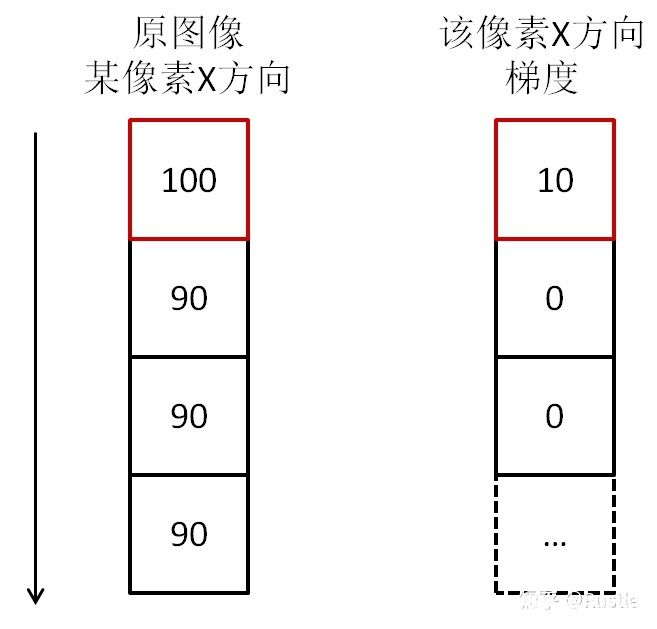
圖 3-1
圖中我們可以看到,100與90之間相差的灰度值為10,即當(dāng)前像素點(diǎn)在X軸方向上的梯度為10,而其它點(diǎn)均為90,則求導(dǎo)后發(fā)現(xiàn)梯度全為0,因此我們可以發(fā)現(xiàn)在數(shù)字圖像處理,因其像素性質(zhì)的特殊性,微積分在圖像處理表現(xiàn)的形式為計(jì)算當(dāng)前像素點(diǎn)沿偏微分方向的差值,所以實(shí)際的應(yīng)用是不需要用到求導(dǎo)的,只需進(jìn)行簡單的加減運(yùn)算
而另一個(gè)概念梯度的模則表示f(x, y),在其最大變化率方向上的單位距離所增加的量,即:
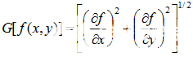
在了解完梯度的概念之后呢,下面我們先介紹一下幾種基本邊緣檢測濾波器: Sobel、Prewitt、Roberts算子
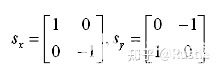
圖 3-2 Roberts算子
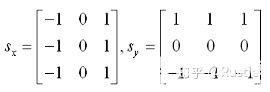
圖 3-2 Prewitt算子
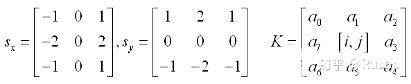
圖 3-3 Sobel算子
我們以Sobel為例,其中
分別表示對于X軸、Y軸的邊緣檢測算子,從
算子結(jié)構(gòu)可以很清楚發(fā)現(xiàn),這個(gè)濾波器是計(jì)算當(dāng)前像素點(diǎn)右邊與左邊8連通像素灰度值的差值,我們先通過一維的概念來理解一下:
如現(xiàn)在有一個(gè)一維數(shù)組長度為10,值為:
[ 8, 6, 2, 4, 9, 1, 3, 5, 10, 6 ]
此時(shí)我們的一維邊緣檢測算子則表現(xiàn)為[ -1, 0, 1 ],現(xiàn)在我們把邊緣檢測算子放在數(shù)組上面進(jìn)行點(diǎn)積(即對應(yīng)點(diǎn)相乘之后的和),得到結(jié)果為:
[ 6, -6, -2, 7, -3, -6, 4, 7, 1, -10]
可以發(fā)現(xiàn)得到的值出現(xiàn)了負(fù)數(shù),但我們之前的定義則聲明了像素灰度值定義域?yàn)?-255范圍內(nèi),因此這里一般的操作為將負(fù)數(shù)截?cái)嗟?-255以內(nèi)或者直接取絕對值,因此現(xiàn)在我們得到的是
[ 6, 6, 2, 7, 3, 6, 4, 7, 1, 10]
其中數(shù)字的大小則表示了當(dāng)前像素點(diǎn)梯度的模大小,即灰度變化的速度有多大,值越大,我們一定程度上就可以確信當(dāng)前點(diǎn)為我們所要找的邊緣點(diǎn),通過一維的例子我們可以更好理解二維的邊緣檢測思想,即沿著X軸、Y軸進(jìn)行兩次濾波操作,得到的結(jié)果進(jìn)行平方求和加根號(hào)的操作得出當(dāng)前像素點(diǎn)的圖像梯度,我們來通過一張圖理解一下這個(gè)過程:

圖 3-4 原圖像、沿X軸梯度圖像、沿Y軸梯度圖像、梯度圖像的可視化
圖中(a)為原始的灰度圖像,(b)和(c)為使用圖3-3中Sobel算子的
兩種形式分別對原始圖像進(jìn)行的濾波結(jié)果,即表示為分別沿X、Y軸的梯度圖,最后將兩個(gè)圖融合在一起則得到了我們所需的梯度圖像(d),在給大家一張圖來幫助理解Sobel算法
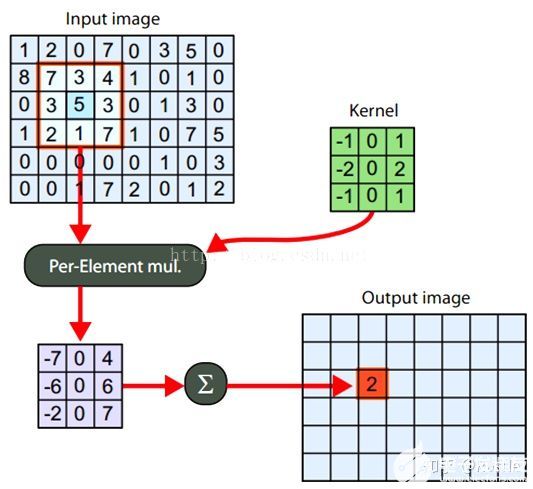
現(xiàn)在我們已經(jīng)大致了解了邊緣檢測的基本思想了,看著圖 3-4(d)是不是覺得它挺好看的呢,但是好看不一定說明它就是我們所需要的邊緣圖,直接用基本的邊緣算子如Sobel求得的邊緣圖存在很多問題,如噪聲污染沒有被排除、邊緣線太過于粗寬等,因此我們接下來要介紹兩個(gè)先進(jìn)的邊緣檢測算子:Canny算子和Marr-Hildreth算子
1.較為先進(jìn)的邊緣檢測算子
1).Canny算子
Canny算子是澳洲計(jì)算機(jī)科學(xué)家約翰·坎尼(John F. Canny)于1986年開發(fā)出來的一個(gè)多級(jí)
邊緣檢測算法,其目標(biāo)是找到一個(gè)最優(yōu)的邊緣,其最優(yōu)邊緣的定義是:
1.好的檢測 --算法能夠盡可能多地標(biāo)示出圖像中的實(shí)際邊緣
2.好的定位 --標(biāo)識(shí)出的邊緣要與實(shí)際圖像中的實(shí)際邊緣盡可能接近
3.最小響應(yīng) --圖像中的邊緣只能標(biāo)識(shí)一次,并且可能存在的圖像噪聲不應(yīng)該標(biāo)識(shí)為邊緣
所以接下來我們來介紹一下目前流行的Canny算法的具體步驟
(1).高斯(Gaussian)濾波
高斯濾波目前是最為流行的去噪濾波算法,高斯與我們學(xué)的概率論中正態(tài)分布中正態(tài)一詞指的是同一個(gè)意思,其原理為根據(jù)待濾波的像素點(diǎn)及其鄰域點(diǎn)的灰度值按照高斯公式生成的參數(shù)規(guī)則進(jìn)行加權(quán)平均,這樣可以有效濾去理想圖像中疊加的高頻噪聲(noise)
二維高斯公式為:
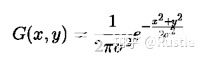
常見的高斯濾波器有:
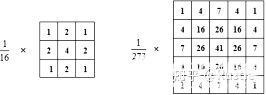
圖 3-5 常見的高斯濾波器
其實(shí)高斯濾波器很像一個(gè)金字塔結(jié)構(gòu),其濾波器的值大小我們可以理解為權(quán)重(weight),值越大對應(yīng)的像素點(diǎn)權(quán)重越大,分量也就越大,因此從高斯濾波器我們可以看出對應(yīng)當(dāng)前像素點(diǎn),距離越遠(yuǎn)權(quán)重越小,對灰度值的貢獻(xiàn)也就越小
讓我們舉個(gè)例子來理解一下高斯濾波,如圖3-5中左邊的高斯濾波器,其中心點(diǎn)4我們可以把它看成是'主人公',其周圍的點(diǎn)看成是'鄰居',噪聲我們把它看成是'壞人',現(xiàn)在我們假設(shè)這9個(gè)人里面,有一個(gè)人是'壞人',我們也知道壞人是肯定會(huì)說自己是好人的,但要是我們有投票機(jī)制決定一個(gè)人是否為'壞人'呢,其中權(quán)重(weight)則對應(yīng)每個(gè)人說話的分量,投票機(jī)制就為我們所說的加權(quán)平均策略,現(xiàn)在我們可以很直觀地發(fā)現(xiàn),其實(shí)高斯濾波就是一個(gè)會(huì)考慮其周圍像素點(diǎn)的濾波器,即使當(dāng)前點(diǎn)位為噪聲點(diǎn),高斯濾波器也會(huì)通過周圍點(diǎn)的灰度值來制約噪聲的影響,生成高斯濾波器與濾波的代碼如下:
sigma=1; %高斯標(biāo)準(zhǔn)差
% 根據(jù)高斯標(biāo)準(zhǔn)差計(jì)算濾波器長度
filterExtent = ceil(4*sigma);
x = -filterExtent:filterExtent;
% 生成一維高斯核
c = 1/(sqrt(2*pi)*sigma);
gaussKernel = c * exp(-(x.^2)/(2*sigma^2));
% 標(biāo)準(zhǔn)化
gaussKernel = gaussKernel/sum(gaussKernel);
% 對圖像進(jìn)行高斯濾波平滑
aSmooth=imfilter(a,gaussKernel,'conv','replicate'); % 沿著X軸卷積
aSmooth=imfilter(aSmooth,gaussKernel','conv','replicate'); % 沿著Y軸卷積
(其中g(shù)aussKernel'表示對gaussKernel進(jìn)行轉(zhuǎn)置)
(2).計(jì)算梯度圖像與角度圖像
計(jì)算梯度圖像我們剛才基本也有理解了一下,無非就是用各種邊緣檢測算子進(jìn)行梯度的檢測,但Canny中使用的梯度檢測算子有點(diǎn)高級(jí),是使用高斯濾波器進(jìn)行梯度計(jì)算得到的濾波器,得到的結(jié)果也類似于Sobel算子,即距離中心點(diǎn)越近的像素點(diǎn)權(quán)重越大,代碼如下:
% 數(shù)值梯度函數(shù)(Gaussian核的生成1-D導(dǎo)數(shù))
derivGaussKernel = gradient(gaussKernel);
% 標(biāo)準(zhǔn)化
negVals = derivGaussKernel < 0;
posVals = derivGaussKernel > 0;
derivGaussKernel(posVals) = derivGaussKernel(posVals)/sum(derivGaussKernel(posVals));
derivGaussKernel(negVals) = derivGaussKernel(negVals)/abs(sum(derivGaussKernel(negVals)));
% 計(jì)算梯度
dx = imfilter(aSmooth, derivGaussKernel, 'conv','replicate');
dy = imfilter(aSmooth, derivGaussKernel', 'conv','replicate');
mag = hypot(dx,dy);
magmax = max(mag(:));
if magmax>0
magGrad = mag / magmax; % 梯度標(biāo)準(zhǔn)化
end
角度圖像的計(jì)算則較為簡單,其作用為非極大值抑制的方向提供指導(dǎo),公式如下:

(3).對梯度圖像進(jìn)行非極大值抑制
從上一步得到的梯度圖像存在邊緣粗寬、弱邊緣干擾等眾多問題,現(xiàn)在我們可以使用非極大值抑制來尋找像素點(diǎn)局部最大值,將非極大值所對應(yīng)的灰度值置0,這樣可以剔除一大部分非邊緣的像素點(diǎn)
如圖 3-6所示,C表示為當(dāng)前非極大值抑制的點(diǎn),g1-4為它的8連通鄰域點(diǎn),圖中藍(lán)色線段表示上一步計(jì)算得到的角度圖像C點(diǎn)的值,即梯度方向,第一步先判斷C灰度值在8值鄰域內(nèi)是否最大,如是則繼續(xù)檢查圖中梯度方向交點(diǎn)dTmp1,dTmp2值是否大于C,如C點(diǎn)大于dTmp1,dTmp2點(diǎn)的灰度值,則認(rèn)定C點(diǎn)為極大值點(diǎn),置為1,因此最后生成的圖像應(yīng)為一副二值圖像,邊緣理想狀態(tài)下都為單像素邊緣
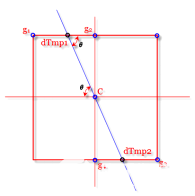
圖 3-6 非極大值抑制
(其中需要注意的是梯度方向交點(diǎn)并不一定落在8領(lǐng)域所在8個(gè)點(diǎn)的位置,因此dTmp1和dTmp2實(shí)際應(yīng)用中是使用相鄰兩個(gè)點(diǎn)的雙線性插值所形成的灰度值)
最后在上一張圖幫助大家理解,如圖3-7所示,其中梯度方向均為垂直向上,經(jīng)過非極大值抑制后取梯度方向上最大值為邊緣點(diǎn),形成細(xì)且準(zhǔn)確的單像素邊緣
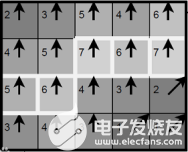
圖 3-7
(4).使用雙閾值進(jìn)行邊緣連接
經(jīng)過以上三步之后得到的邊緣質(zhì)量已經(jīng)很高了,但還是存在很多偽邊緣,因此Canny算法中所采用的算法為雙閾值法,具體思路為選取兩個(gè)閾值,將小于低閾值的點(diǎn)認(rèn)為是假邊緣置0,將大于高閾值的點(diǎn)認(rèn)為是強(qiáng)邊緣置1,介于中間的像素點(diǎn)需進(jìn)行進(jìn)一步的檢查
根據(jù)高閾值圖像中把邊緣鏈接成輪廓,當(dāng)?shù)竭_(dá)輪廓的端點(diǎn)時(shí),該算法會(huì)在斷點(diǎn)的8鄰域點(diǎn)中尋找滿足低閾值的點(diǎn),再根據(jù)此點(diǎn)收集新的邊緣,直到整個(gè)圖像閉合,具體代碼為:
function nedge=connect1(nedge,y,x,low,high,magGrad) %種子定位后的連通分析
neighbour=[-1 -1;-1 0;-1 1;0 -1;0 1;1 -1;1 0;1 1]; %八連通搜尋
[m n]=size(nedge);
for k=1:8
yy=fix(y+neighbour(k,1));
xx=fix(x+neighbour(k,2));
if yy>=1 &&yy<=m &&xx>=1 && xx<=n
if magGrad(yy,xx)>=low & nedge(yy,xx)~=255 & magGrad(yy,xx)
但由于尋找弱邊緣點(diǎn)的計(jì)算代價(jià)過大,因?yàn)槭褂玫氖沁f歸思維,且所找尋到的弱邊緣點(diǎn)為數(shù)不多,因此實(shí)際應(yīng)用中常常舍去這一步驟,取而代之的是基于形態(tài)學(xué)的邊緣細(xì)化操作,具體思想我們以后還會(huì)提到,具體代碼為:
H = bwmorph(H, 'thin', 1);
至此,我們已經(jīng)深度理解了Canny算法的思想與實(shí)現(xiàn)手段,實(shí)際應(yīng)用中Canny一般是邊緣檢測的首選項(xiàng),其算法思想也非常值得我們學(xué)習(xí),接下來我們在簡單介紹基于二階導(dǎo)數(shù)法的Marr-Hildreth邊緣檢測算子
1).Marr-Hildreth算子
在學(xué)習(xí)Marr-Hildreth算子之前我們先來理解一下為什么要用二階導(dǎo)數(shù)法
如圖 3-8所示,左邊表示的是一副灰度圖像,從左到右從黑色(0)慢慢變?yōu)榘咨?255),現(xiàn)在我們來看它的水平灰度剖面,灰度值從小到大平穩(wěn)上升,其一階導(dǎo)數(shù)表示為在上升區(qū)域?yàn)椴蛔兊闹担渲械玫降男畔⑹菆D像灰度值是平穩(wěn)過渡的,即梯度值相等,接下來在將其求二次導(dǎo)數(shù),得到的圖像為在開始過渡的起點(diǎn)為正數(shù),其值為一階導(dǎo)數(shù)在此點(diǎn)的梯度值,結(jié)束點(diǎn)也和起點(diǎn)一樣,現(xiàn)在重點(diǎn)來了,我們將這兩點(diǎn)連起來得到一個(gè)與X軸的交叉點(diǎn),這一點(diǎn)就是我們所認(rèn)為的邊緣點(diǎn),這就是二階導(dǎo)數(shù)應(yīng)用在邊緣檢測領(lǐng)域的奇妙之處(第一次接觸的時(shí)候覺得巨神奇)
在看一下marr和hildreth的證明結(jié)論:
1.灰度變化與圖像尺寸無關(guān),因此他們的檢測要求使用不同尺寸的算子
2.灰度的突然變換會(huì)在一階導(dǎo)數(shù)中引起波峰或波谷,在二階導(dǎo)數(shù)中等效引起零交叉
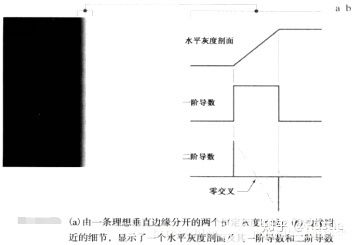
圖 3-8 零交叉原理
學(xué)習(xí)了基于二階導(dǎo)數(shù)的馬爾哈希算法原理之后,我們來看一下它的思路:
(1).高斯濾波
對你沒看錯(cuò),還是高斯濾波,基本所有邊緣檢測算法前面都會(huì)加一個(gè)高斯濾波來去除高頻噪聲,所以這里不在多說了,大家往前回顧一下就好了
(2).計(jì)算拉普拉斯(Laplacian)二階導(dǎo)
Marr-Hildreth證明,最滿足圖像處理需求的算子是濾波器拉普拉斯高斯(Log)算子,具體原理我們不在多做闡述,這里我們來看一下它的公式:
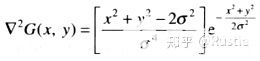
由其生成的拉普拉斯濾波器也被稱為墨西哥草帽算子,因?yàn)槠渲虚g一般為較大的正數(shù),8鄰域連通點(diǎn)為較小的負(fù)數(shù)值,常用的濾波器如圖 3-9所示:

圖 3-9 拉普拉斯濾波器
之后就是使用拉普拉斯濾波器進(jìn)行圖像的濾波操作,得到待計(jì)算圖像
(3).計(jì)算零交叉(Zero crossing)
零交叉的實(shí)現(xiàn)較為簡單,由于零交叉點(diǎn)意味著至少兩個(gè)相鄰的像素點(diǎn)的像素值異號(hào),一共有四種需要檢測的情況:左右,上下,兩個(gè)對角,其中如果濾波后的圖像g(x, y)的任意像素p處的四種情況其中一組的差值的絕對值超過了設(shè)定的閾值,則我們可以稱p為一個(gè)零交叉像素,示例如下:

圖 3-10
此為Marr-Hildreth其中一小部分,檢測[ - +]這一情況是否滿足,其中thresh為提到的閾值
到這里我們就學(xué)習(xí)了兩種最為流行且經(jīng)典的先進(jìn)邊緣檢測算法與思想,接下來說的是一些經(jīng)驗(yàn)與算法的選擇參考
四.補(bǔ)充
1.濾波器的大小應(yīng)該是奇數(shù),這樣才有一個(gè)中心點(diǎn)可進(jìn)行賦值操作,常見的濾波器或卷積核(Conv kernel)有3*3、5*5等,因此也有了半徑的概念,例如5*5的卷積核的半徑為2
2.濾波器中所有元素之和應(yīng)為0,這一限制條件是保證濾波前后圖像總體灰度值不變
3.Roberts算子、Sobel算子、Prewitt算子運(yùn)算速率高,對噪聲也有一定抑制作用,但檢測出的邊緣質(zhì)量不高,如邊緣較粗、定位不準(zhǔn)、間斷點(diǎn)多
4.Canny算子不容易受噪聲干擾,得到的邊緣精細(xì)且準(zhǔn)確,缺點(diǎn)就是運(yùn)算代價(jià)較高,運(yùn)行于實(shí)時(shí)圖像處理較困難,適用于高精度要求的應(yīng)用
5.Marr-Hildreth算子邊緣檢測效果相對較優(yōu),但對于噪聲比較敏感(因其二階運(yùn)算的性質(zhì))
五.總結(jié)
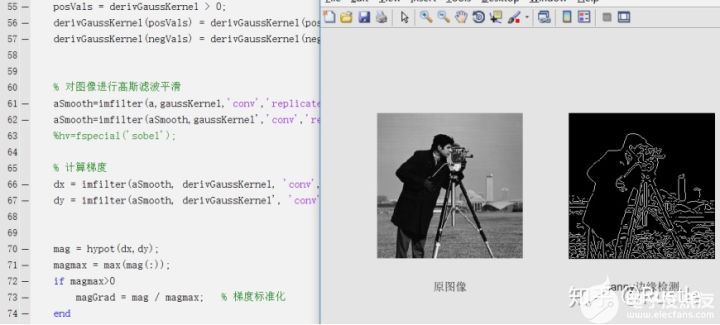
總體來說,邊緣檢測算法應(yīng)用面非常廣,遍及很多領(lǐng)域,是入門計(jì)算機(jī)視覺(Computer vision)學(xué)習(xí)一個(gè)非常好的途徑,其中很多思想和原理的東西至今對筆者也有印象,所以筆者第一篇文章就想著從這個(gè)開始寫,還有就是文章有些地方是筆者自己的一些理解和見解,如有錯(cuò)誤的地方希望大家?guī)兔χ赋鰜砉院筮€會(huì)繼續(xù)寫一些關(guān)于機(jī)器學(xué)習(xí)(Machine learning)、深度學(xué)習(xí)(Deep learning)、人臉識(shí)別(Face recognition)的文章,最后附上Canny邊緣檢測算法完整的Matlab代碼實(shí)現(xiàn)(當(dāng)然也可以調(diào)用edge函數(shù),但是學(xué)習(xí)的話最好自己從底層實(shí)現(xiàn)一遍嘛是吧)
I=imread('cameraman.tif');
%I=rgb2gray(I);
figure(1);subplot(121);imshow(I);xlabel('原圖像');
[m n]=size(I);
a=double(I);
sigma=1; %高斯標(biāo)準(zhǔn)差
%highThresh=0.0625; %上閾值
%lowThresh=0.0250 ; %下閾值
%=======================高斯濾波&梯度計(jì)算=======================
%%%%%%%%%%%%%%%%%%%%%%%%%Old%%%%%%%%%%%%%%%%%%%%%%%%%%%
%pw = 1:30;
%ssq = sigma^2;
%width = find(exp(-(pw.*pw)/(2*ssq))>0.0001,1,'last');
%if isempty(width)
% width = 1;
%end
%t = (-width:width);
%gauss = exp(-(t.*t)/(2*ssq))/(2*pi*ssq); % 一維高斯濾波器
%[x,y]=meshgrid(-width:width,-width:width);
%gauss2=-x.*exp(-(x.*x+y.*y)/(2*ssq))/(pi*ssq); %二維高斯濾波器
%對圖像進(jìn)行高斯濾波平滑
%aSmooth=imfilter(a,gauss,'conv','replicate'); % 沿著X軸卷積
%aSmooth=imfilter(aSmooth,gauss','conv','replicate'); % 沿著Y軸卷積
%使用二維高斯對圖像進(jìn)行卷積
%dx = imfilter(aSmooth, gauss2, 'conv','replicate');
%dy = imfilter(aSmooth, gauss2', 'conv','replicate');
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 根據(jù)高斯標(biāo)準(zhǔn)差計(jì)算濾波器長度
filterExtent = ceil(4*sigma);
x = -filterExtent:filterExtent;
% 生成一維高斯核
c = 1/(sqrt(2*pi)*sigma);
gaussKernel = c * exp(-(x.^2)/(2*sigma^2));
% 標(biāo)準(zhǔn)化
gaussKernel = gaussKernel/sum(gaussKernel);
% 數(shù)值梯度函數(shù)(Gaussian核的生成1-D導(dǎo)數(shù))
derivGaussKernel = gradient(gaussKernel);
% 標(biāo)準(zhǔn)化
negVals = derivGaussKernel < 0;
posVals = derivGaussKernel > 0;
derivGaussKernel(posVals) = derivGaussKernel(posVals)/sum(derivGaussKernel(posVals));
derivGaussKernel(negVals) = derivGaussKernel(negVals)/abs(sum(derivGaussKernel(negVals)));
% 對圖像進(jìn)行高斯濾波平滑
aSmooth=imfilter(a,gaussKernel,'conv','replicate'); % 沿著X軸卷積
aSmooth=imfilter(aSmooth,gaussKernel','conv','replicate'); % 沿著Y軸卷積
%hv=fspecial('sobel');
% 計(jì)算梯度
dx = imfilter(aSmooth, derivGaussKernel, 'conv','replicate');
dy = imfilter(aSmooth, derivGaussKernel', 'conv','replicate');
mag = hypot(dx,dy);
magmax = max(mag(:));
if magmax>0
magGrad = mag / magmax; % 梯度標(biāo)準(zhǔn)化
end
% 閾值選擇
%PercentOfPixelsNotEdges = 0.7;
counts=imhist(magGrad, 64);
highThresh = find(cumsum(counts) > 0.7*m*n, 1 ,'first' ) / 64;
lowThresh = 0.4*highThresh;
%figure(8);imshow(magGrad);
%%========================高斯濾波========================================
%w=fspecial('gaussian',[5 5]);
%img=imfilter(img,w,'replicate');
%figure;
%imshow(uint8(img))
%%===================sobel邊緣檢測=======================================
%hv=fspecial('sobel');
%dx=imfilter(img,hv,'replicate'); %求橫邊緣
%hh=hv';
%dy=imfilter(img,hh,'replicate'); %求豎邊緣
%img=sqrt(dx.^2+dy.^2);
% magmax = max(img(:));% (閾值選擇歸一化)
% if magmax > 0
% magGrad = img / magmax;
% end
%figure;
%imshow(uint8(img));
I = thinAndThreshold(dx, dy, magGrad, lowThresh, highThresh);
%disp(lowThresh);
subplot(122);imshow(I);xlabel('canny邊緣檢測');
disp("高閾值TL: "+highThresh);
disp("低閾值TH: "+lowThresh);
%========================非極大值抑制和邊緣連接=======================================
function H = thinAndThreshold(dx, dy, magGrad, lowThresh, highThresh)
E = cannyFindLocalMaxima(dx,dy,magGrad,lowThresh); %非極大值抑制
if ~isempty(E)
[rstrong,cstrong] = find(magGrad>highThresh & E);
if ~isempty(rstrong)
H = bwselect(E, cstrong, rstrong, 8); % 選定強(qiáng)邊緣8連通目標(biāo)
% figure(2);imshow(H);
% set(0,'RecursionLimit',1000); %弱邊緣連通(無太大作用,且運(yùn)算時(shí)間過長)
% [xstrong ystrong]=find(magGrad>highThresh & E);
% for i=1:numel(xstrong);
% H = connect1(H,xstrong(i),ystrong(i),lowThresh,highThresh,magGrad);
% end
% figure(3);imshow(H);
H = bwmorph(H, 'thin', 1); % 邊緣細(xì)化
else
H = false(size(E));
end
else
H = false(size(E));
end
end
%========================弱邊緣連接=======================================
function nedge=connect1(nedge,y,x,low,high,magGrad) %種子定位后的連通分析
neighbour=[-1 -1;-1 0;-1 1;0 -1;0 1;1 -1;1 0;1 1]; %八連通搜尋
[m n]=size(nedge);
for k=1:8
yy=fix(y+neighbour(k,1));
xx=fix(x+neighbour(k,2));
if yy>=1 &&yy<=m &&xx>=1 && xx<=n
if magGrad(yy,xx)>=low & nedge(yy,xx)~=255 & magGrad(yy,xx)
效果如圖所示:
-
圖像處理
+關(guān)注
關(guān)注
27文章
1295瀏覽量
56803 -
圖像處理技術(shù)
+關(guān)注
關(guān)注
0文章
33瀏覽量
10076 -
邊緣檢測
+關(guān)注
關(guān)注
0文章
92瀏覽量
18224 -
圖像處理算法
+關(guān)注
關(guān)注
0文章
10瀏覽量
2584
發(fā)布評(píng)論請先 登錄
相關(guān)推薦
基于FPGA的實(shí)時(shí)邊緣檢測系統(tǒng)設(shè)計(jì),Sobel圖像邊緣檢測,F(xiàn)PGA圖像處理
基于FPGA的嵌入式圖像邊緣檢測系統(tǒng)設(shè)計(jì)
基于FPGA的數(shù)字圖像處理中的邊緣檢測系統(tǒng)
如何利用FPGA實(shí)現(xiàn)Laplacian圖像邊緣檢測器的研究?
源碼交流=圖像處理 實(shí)現(xiàn)圖像去噪、濾波、銳化、邊緣檢測
怎樣去設(shè)計(jì)基于FPGA的實(shí)時(shí)圖像邊緣檢測系統(tǒng)
基于FPGA的實(shí)時(shí)圖像邊緣檢測系統(tǒng)設(shè)計(jì)(附代碼)
實(shí)時(shí)圖像邊緣檢測的設(shè)計(jì)及FPGA實(shí)現(xiàn)
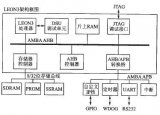
基于LEON3開源軟核處理器的動(dòng)態(tài)圖像邊緣檢測SoC設(shè)計(jì)




 圖像處理技術(shù)的應(yīng)用:邊緣檢測
圖像處理技術(shù)的應(yīng)用:邊緣檢測










評(píng)論