多年來,我們已經看到許多領域和行業利用人工智能 (AI) 的力量來推動研究的邊界。數據壓縮和重建也不例外,人工智能的應用可以用來構建更強大的系統。
在本文中,我們將研究一個非常流行的 AI 用例,用于壓縮數據并使用自動編碼器重建壓縮數據。
自動編碼器應用
自動編碼器在機器學習領域引起了許多人的關注,這一事實通過自動編碼器的改進和幾種變體的發明變得顯而易見。他們在神經機器翻譯、藥物發現、圖像去噪等幾個領域取得了一些有希望的(如果不是最先進的)結果。
自動編碼器的組成部分
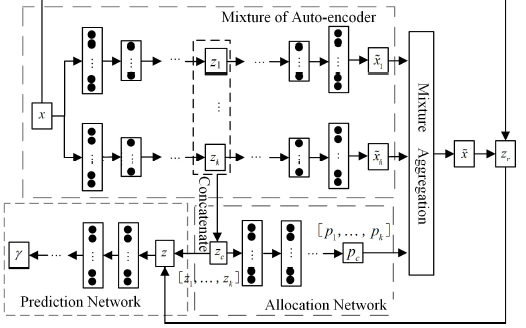
與大多數神經網絡一樣,自編碼器通過反向傳播梯度來優化一組權重——但自編碼器架構與大多數神經網絡架構之間最顯著的區別是瓶頸。這個瓶頸是將我們的數據壓縮成較低維度的表示的一種手段。自編碼器的另外兩個重要部分是編碼器和解碼器。
將這三個組件融合在一起形成了一個“香草”自動編碼器,盡管更復雜的自動編碼器可能有一些額外的組件。
讓我們分別看一下這些組件。
編碼器
這是數據壓縮和重建的第一階段,它實際上負責數據壓縮階段。編碼器是一個前饋神經網絡,它接收數據特征(例如圖像壓縮中的像素)并輸出一個大小小于數據特征大小的潛在向量。
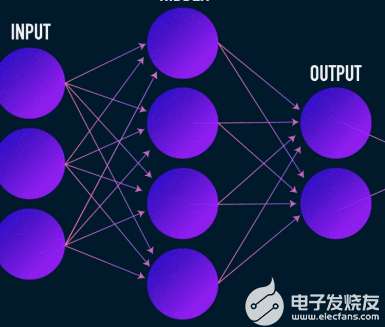
為了使數據的重建具有魯棒性,編碼器在訓練期間優化其權重,以將輸入數據表示的最重要特征壓縮到小型潛在向量中。這確保了解碼器有足夠的關于輸入數據的信息來以最小的損失重建數據。
潛在向量(瓶頸)
自編碼器的瓶頸或潛在向量分量是最關鍵的部分——當我們需要選擇它的大小時,它變得更加關鍵。
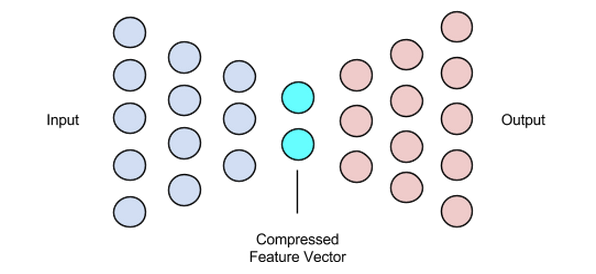
編碼器的輸出為我們提供了潛在向量,并且應該包含我們輸入數據的最重要的特征表示。它還用作解碼器部分的輸入,并將有用的表示傳播到解碼器進行重建。
為潛在向量選擇更小的尺寸意味著我們可以用更少的輸入數據信息來表示輸入數據特征。選擇更大的潛在向量大小會淡化使用自動編碼器進行壓縮的整個想法,并且還會增加計算成本。
解碼器
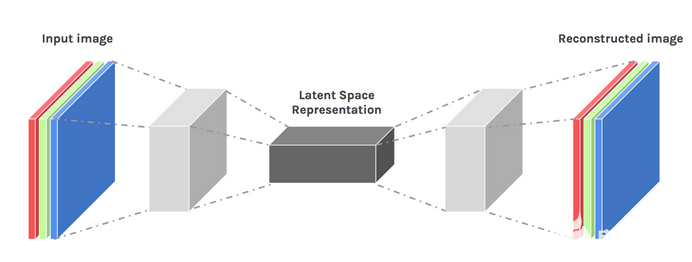
這個階段結束了我們的數據壓縮和重建過程。就像編碼器一樣,這個組件也是一個前饋神經網絡,但它在結構上看起來與編碼器有點不同。這種差異來自這樣一個事實,即解碼器將一個比解碼器輸出更小的潛在向量作為輸入。
解碼器的功能是從與輸入非常接近的潛在向量生成輸出。
訓練自動編碼器
通常,在訓練自動編碼器時,我們將這些組件一起構建,而不是獨立構建。我們使用梯度下降或 ADAM 優化器等優化算法對它們進行端到端訓練。
損失函數
值得討論的自動編碼器訓練過程的一部分是損失函數。數據重建是一項生成任務,與其他機器學習任務不同,我們的目標是最大化預測正確類別的概率,我們驅動我們的網絡產生接近輸入的輸出。
我們可以通過幾個損失函數來實現這個目標,例如 l1、l2、均方誤差等。這些損失函數的共同點是它們測量輸入和輸出之間的差異(即多遠或相同),使它們中的任何一個成為合適的選擇。
自動編碼器網絡
一直以來,我們一直在使用多層感知器來設計我們的編碼器和解碼器——但事實證明,我們可以使用更專業的框架,例如卷積神經網絡 (CNN) 來捕獲更多關于輸入數據的空間信息圖像數據壓縮的情況。
令人驚訝的是,研究表明,用作文本數據自動編碼器的循環網絡工作得非常好,但我們不打算在本文的范圍內進行討論。多層感知器中使用的編碼器-潛在向量-解碼器的概念仍然適用于卷積自動編碼器。唯一的區別是我們設計了帶有卷積層的解碼器和編碼器。
所有這些自動編碼器網絡都可以很好地完成壓縮任務,但存在一個問題。
我們討論過的網絡創造力為零。我所說的零創造力的意思是他們只能產生他們已經看到或接受過培訓的輸出。
我們可以通過稍微調整我們的架構設計來激發一定程度的創造力。結果被稱為變分自動編碼器。
變分自編碼器
變分自動編碼器引入了兩個主要的設計變化:
我們沒有將輸入轉換為潛在編碼,而是輸出兩個參數向量:均值和方差。
一個稱為 KL 散度損失的附加損失項被添加到初始損失函數中。
變分自動編碼器背后的想法是,我們希望我們的解碼器使用從由編碼器生成的均值向量和方差向量參數化的分布中采樣的潛在向量來重建我們的數據。
從分布中采樣特征給解碼器一個受控的空間來生成。在訓練變分自動編碼器后,每當我們對輸入數據執行前向傳遞時,編碼器都會生成一個均值和方差向量,負責確定從哪個分布中對潛在向量進行采樣。
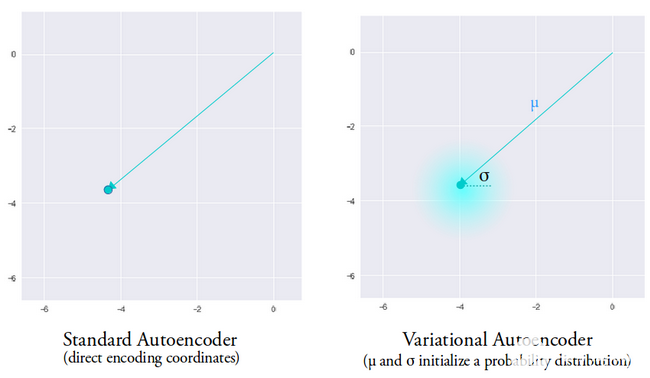
平均向量決定了輸入數據的編碼應該集中在哪里,方差決定了我們想要從中選擇編碼以生成真實輸出的徑向空間或圓。這意味著,對于相同輸入數據的每次前向傳遞,我們的變分自動編碼器可以生成以均值向量為中心和方差空間內的不同輸出變體。
相比之下,在查看標準自動編碼器時,當我們嘗試生成網絡尚未訓練的輸出時,由于編碼器產生的潛在向量空間的不連續性,它會生成不切實際的輸出。
現在我們對變分自動編碼器有了一個直觀的了解,讓我們看看如何在 TensorFlow 中構建一個。
我們將從準備好數據集開始我們的示例。為簡單起見,我們將使用 MNIST 數據集。
(train_images, _), (test_images, _) = tf.keras.datasets.mnist.load_data()
train_images = train_images.reshape(train_images.shape[0], 28, 28, 1).astype(‘float32’)
test_images = test_images.reshape(test_images.shape[0], 28, 28, 1).astype(‘float32’)
# Normalizing the images to the range of [0., 1.]
train_images /= 255.
test_images /= 255.
# Binarization
train_images[train_images 》= .5] = 1.
train_images[train_images 《 .5] = 0.
test_images[test_images 》= .5] = 1.
test_images[test_images 《 .5] = 0.
TRAIN_BUF = 60000
BATCH_SIZE = 100
TEST_BUF = 10000
train_dataset = tf.data.Dataset.from_tensor_slices(train_images).shuffle(TRAIN_BUF).batch(BATCH_SIZE)
test_dataset = tf.data.Dataset.from_tensor_slices(test_images).shuffle(TEST_BUF).batch(BATCH_SIZE)
Obtain dataset and prepare it for the task.
class CVAE(tf.keras.Model):
def __init__(self, latent_dim):
super(CVAE, self).__init__()
self.latent_dim = latent_dim
self.inference_net = tf.keras.Sequential(
[
tf.keras.layers.InputLayer(input_shape=(28, 28, 1)),
tf.keras.layers.Conv2D(
filters=32, kernel_size=3, strides=(2, 2), activation=‘relu’),
tf.keras.layers.Conv2D(
filters=64, kernel_size=3, strides=(2, 2), activation=‘relu’),
tf.keras.layers.Flatten(),
# No activation
tf.keras.layers.Dense(latent_dim + latent_dim),
]
)
self.generative_net = tf.keras.Sequential(
[
tf.keras.layers.InputLayer(input_shape=(latent_dim,)),
tf.keras.layers.Dense(units=7*7*32, activation=tf.nn.relu),
tf.keras.layers.Reshape(target_shape=(7, 7, 32)),
tf.keras.layers.Conv2DTranspose(
filters=64,
kernel_size=3,
strides=(2, 2),
padding=“SAME”,
activation=‘relu’),
tf.keras.layers.Conv2DTranspose(
filters=32,
kernel_size=3,
strides=(2, 2),
padding=“SAME”,
activation=‘relu’),
# No activation
tf.keras.layers.Conv2DTranspose(
filters=1, kernel_size=3, strides=(1, 1), padding=“SAME”),
]
)
@tf.function
def sample(self, eps=None):
if eps is None:
eps = tf.random.normal(shape=(100, self.latent_dim))
return self.decode(eps, apply_sigmoid=True)
def encode(self, x):
mean, logvar = tf.split(self.inference_net(x), num_or_size_splits=2, axis=1)
return mean, logvar
def reparameterize(self, mean, logvar):
eps = tf.random.normal(shape=mean.shape)
return eps * tf.exp(logvar * .5) + mean
def decode(self, z, apply_sigmoid=False):
logits = self.generative_net(z)
if apply_sigmoid:
probs = tf.sigmoid(logits)
return probs
return logits
這兩個代碼片段準備了我們的數據集并構建了我們的變分自動編碼器模型。在模型代碼片段中,有幾個輔助函數來執行編碼、采樣和解碼。
計算梯度的重新參數化
有一個我們尚未討論的重新參數化函數,但它解決了我們的變分自動編碼器網絡中的一個非常關鍵的問題。回想一下,在解碼階段,我們從由編碼器生成的均值和方差向量控制的分布中對潛在向量編碼進行采樣。這在通過我們的網絡前向傳播數據時不會產生問題,但在從解碼器到編碼器的反向傳播梯度時會導致一個大問題,因為采樣操作是不可微的。
簡單來說,我們無法從采樣操作中計算梯度。
這個問題的一個很好的解決方法是應用重新參數化技巧。其工作原理是首先生成均值為 0 和方差為 1 的標準高斯分布,然后使用編碼器生成的均值和方差對該分布執行可微加法和乘法運算。
請注意,我們在代碼中將方差轉換為對數空間。這是為了確保數值穩定性。引入了額外的損失項Kullback-Leibler 散度損失,以確保我們生成的分布盡可能接近均值為 0 方差為 1 的標準高斯分布。
將分布的均值驅動為零可確保我們生成的分布彼此非常接近,以防止分布之間的不連續性。接近 1 的方差意味著我們有一個更適中的(即,不是很大也不是很小)的空間來生成編碼。
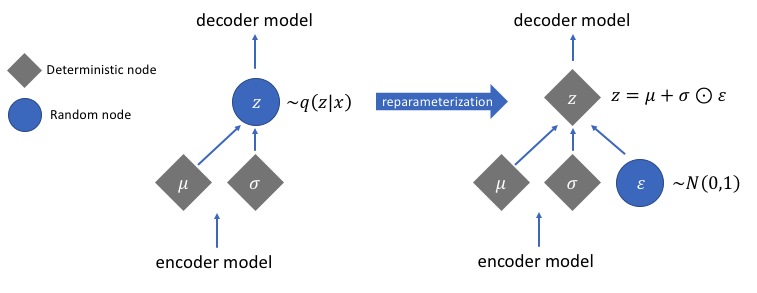
執行重新參數化技巧后,通過將方差向量與標準高斯分布相乘并將結果與??均值向量相加得到的分布與均值和方差向量立即控制的分布非常相似。
構建變分自編碼器的簡單步驟
讓我們通過總結構建變分自動編碼器的步驟來結束本教程:
構建編碼器和解碼器網絡。
在編碼器和解碼器之間應用重新參數化技巧以允許反向傳播。
端到端訓練兩個網絡。
-
編碼器
+關注
關注
45文章
3638瀏覽量
134428 -
tensorflow
+關注
關注
13文章
329瀏覽量
60528
發布評論請先 登錄
相關推薦

基于變分自編碼器的異常小區檢測
稀疏邊緣降噪自動編碼器的方法
基于動態dropout的改進堆疊自動編碼機方法
自動編碼器的社區發現算法
自動編碼器與PCA的比較
稀疏自編碼器及TensorFlow實現詳解
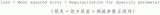
如何使用深度神經網絡技術實現機器學習的全噪聲自動編碼器
一種改進的基于半自動編碼器的協同過濾推薦算法

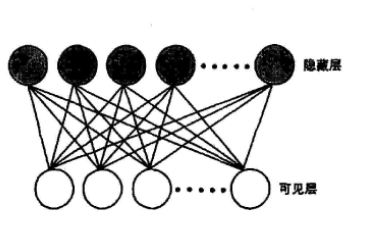
一種混合自動編碼器高斯混合模型MAGMM
一種基于變分自編碼器的人臉圖像修復方法

堆疊降噪自動編碼器(SDAE)
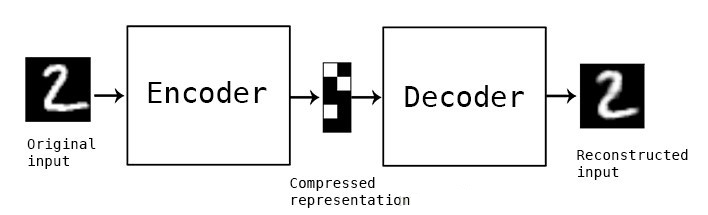




 如何使用TensorFlow構建和訓練變分自動編碼器
如何使用TensorFlow構建和訓練變分自動編碼器










評論