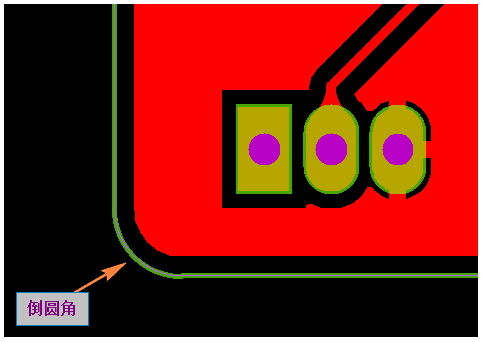
當PCB外形是直角時,通常工程制作外形(鑼帶）時,會將直角或尖角的地方倒成圓角，主要是為了防止PCB容易劃傷板他扎傷人。

所以當客戶沒有特殊要求時,PCB外形是直角一般會默認倒角0.5mm圓角(如下圖所示)

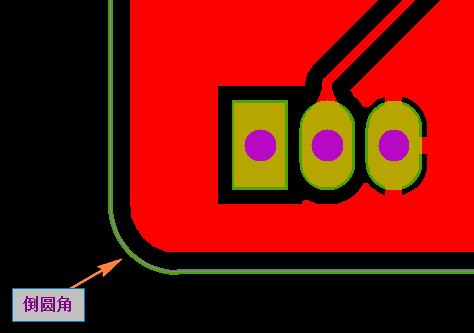
一.PCB板邊倒圓角點分析

原PCB外形如下圖圖示:看了這個PCB外形,產生有2個問題點：

1.外形中哪些點需倒圓角?

2.如何怎么倒圓角?

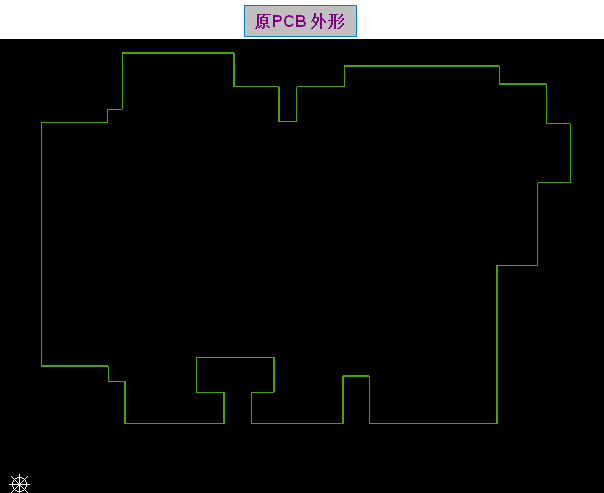
1.外形中哪些點需倒圓角?

看下圖: PCB外形倒圓角的點,剛好就是我們凸包需求出的點,接下來我們將玩轉凸包了,只要求出凸包，那么就可以實現PCB板邊倒圓角啦。

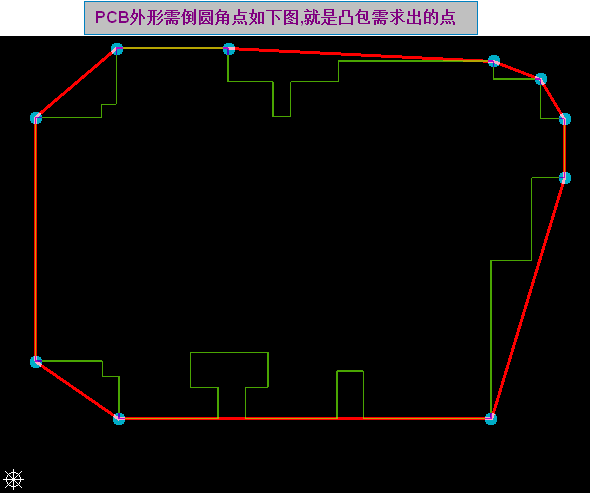
求凸包的算法：我們可以借鑒算法導論中的查找凸包的算法（加以改進得到新的求凸包方法，詳見【方法一】與【方法二】）

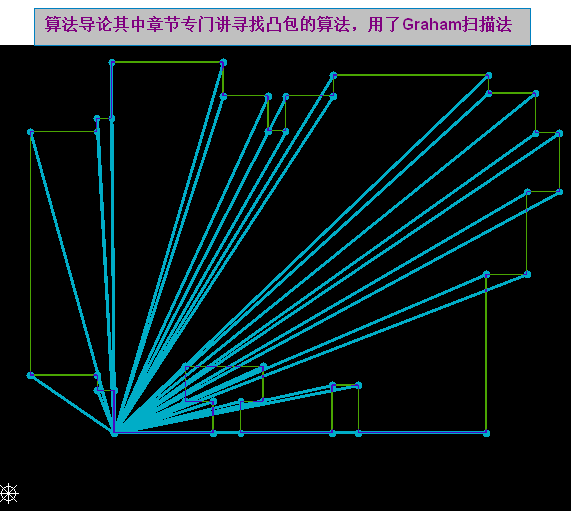
2.如何倒圓角?

在下面有說明倒角方法.

二. 求凸點

方法一求凸點:【采用多輪遍歷,一遍一遍將凹點踢除，剩于的即是凸點】

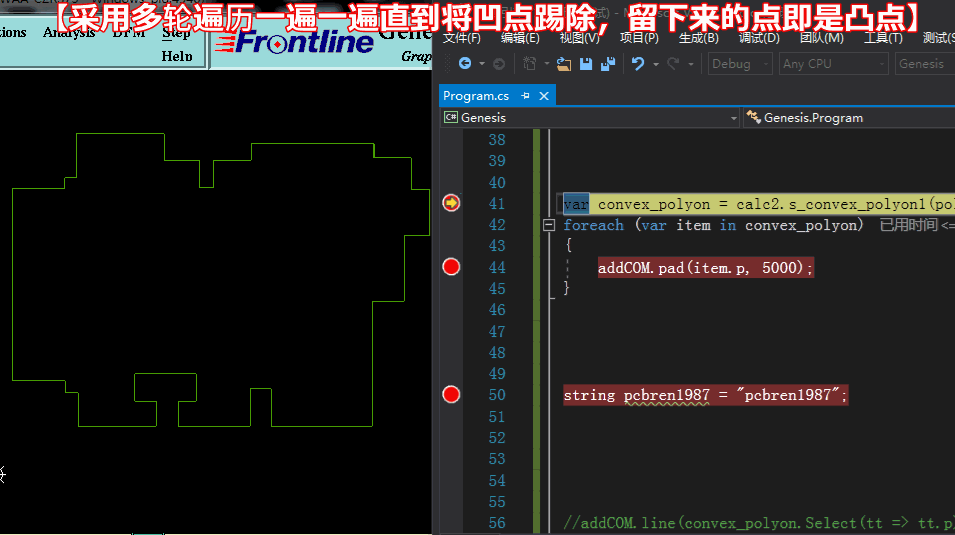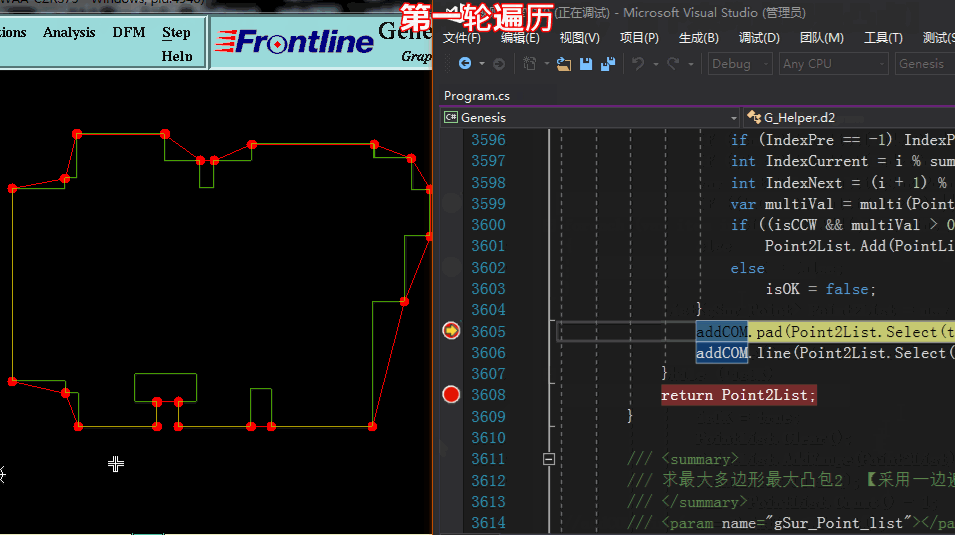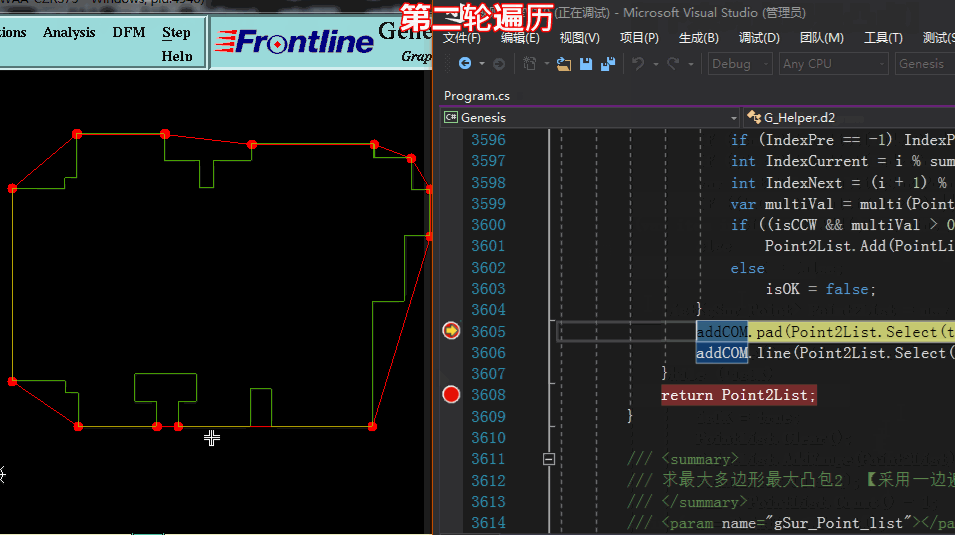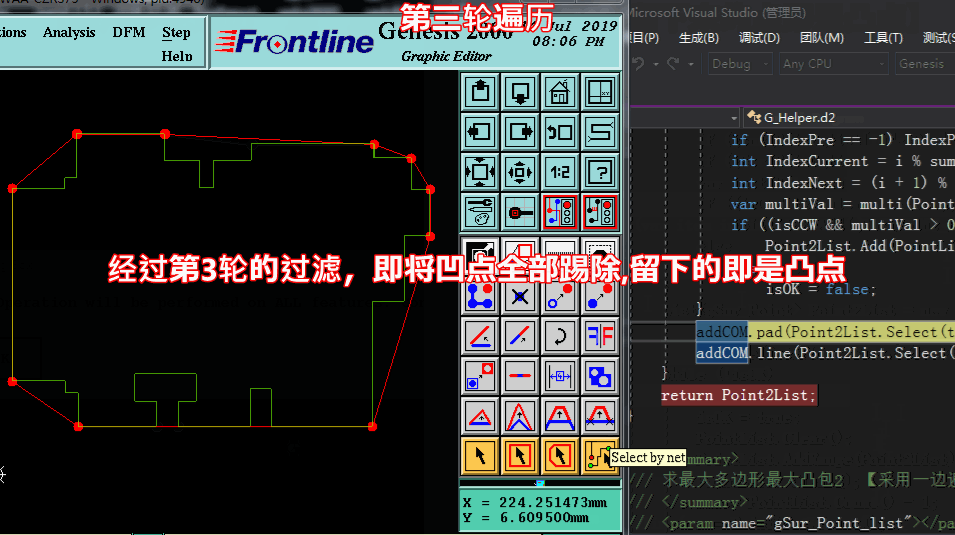
方法一求凸點: 代碼

        /// 

        /// 求最大多邊形最大凸包1  【采用多輪遍歷將凹點踢除，剩于的即是凸點】
        /// 
        /// 
        /// 
        public List s_convex_polyon1(List gSur_Point_list)
        {
            add addCOM = new add();
            bool isOK = true;
            List PointList = new List();
            var isCCW = s_isCCW(gSur_Point_list);
            int sum = gSur_Point_list.Count() - 1;
            int n = gSur_Point_list.Count();
            for (int i = 0; i < n; i++)
            {
                int IndexPre = (i - 1) % sum;
                if (IndexPre == -1) IndexPre = sum - 1;
                int IndexCurrent = i % sum;
                int IndexNext = (i + 1) % sum;
                if (gSur_Point_list[IndexPre].type_point > 0) continue;
                if (gSur_Point_list[IndexCurrent].type_point > 0) continue;
                var multiVal = multi(gSur_Point_list[IndexPre].p, gSur_Point_list[IndexCurrent].p, gSur_Point_list[IndexNext].p);
                if ((isCCW && multiVal > 0) || (!isCCW && multiVal < 0))
                    PointList.Add(gSur_Point_list[IndexCurrent]);
                else
                    isOK = false;
            }
            List Point2List = new List(PointList);
            while (!isOK)
            {
                isOK = true;
                PointList.Clear();
                PointList.AddRange(Point2List);
                Point2List.Clear();
                sum = PointList.Count() - 1;
                n = PointList.Count();
                for (int i = 0; i < n; i++)
                {
                    int IndexPre = (i - 1) % sum;
                    if (IndexPre == -1) IndexPre = sum - 1;
                    int IndexCurrent = i % sum;
                    int IndexNext = (i + 1) % sum;
                    var multiVal = multi(PointList[IndexPre].p, PointList[IndexCurrent].p, PointList[IndexNext].p);
                    if ((isCCW && multiVal > 0) || (!isCCW && multiVal < 0))
                        Point2List.Add(PointList[IndexCurrent]);
                    else
                        isOK = false;
                }
            }
            return Point2List;
        }

方法二求凸包：【采用一邊遍歷找出凸點并加入隊列，并同時將隊列中的凸點隊列中找出凹點踢除】

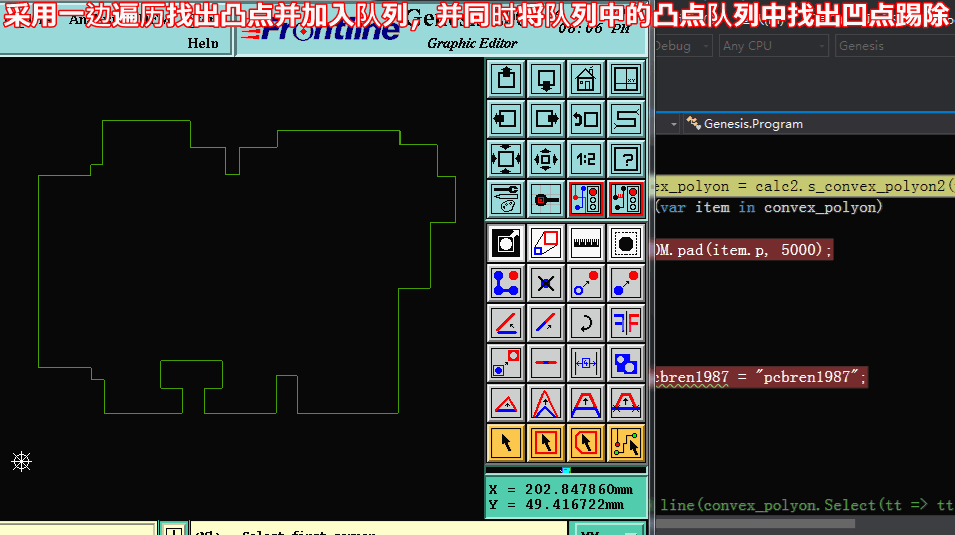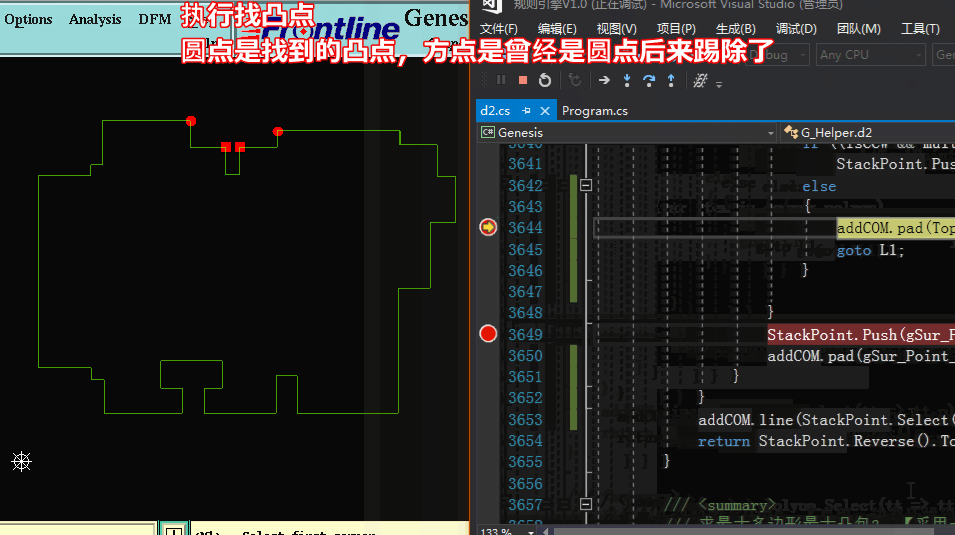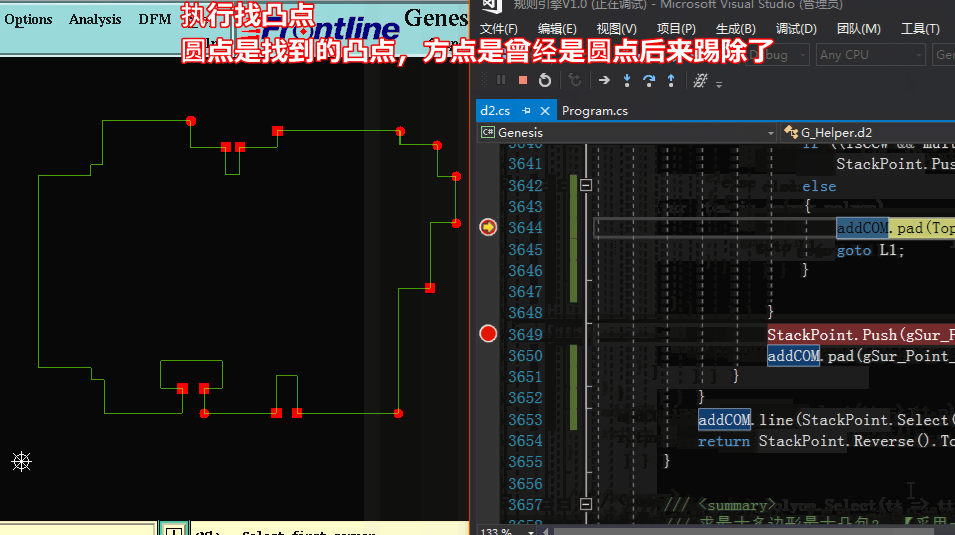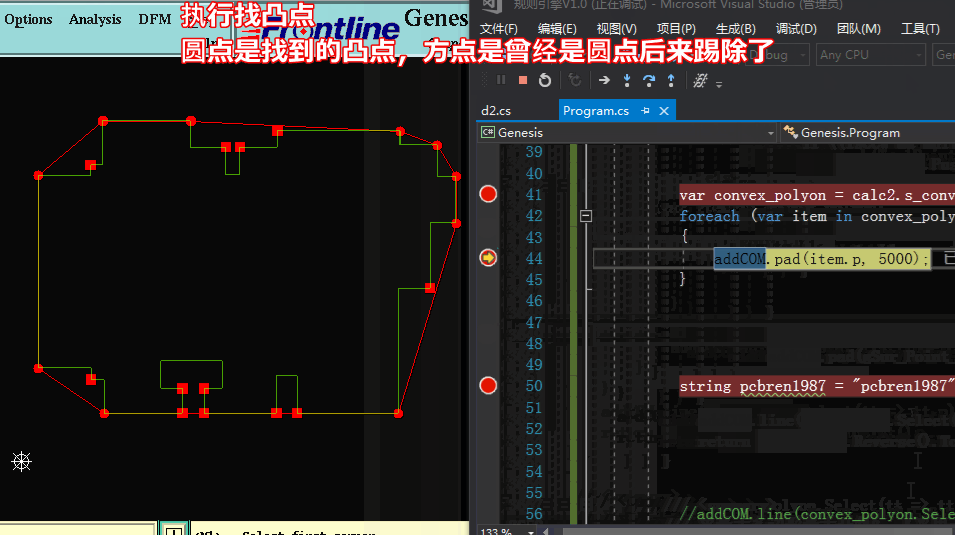
方法二求凸包代碼:

        /// 

        /// 求最大多邊形最大凸包2  【采用一邊遍歷找出凸點并加入隊列，并同時將隊列中的凸點隊列中找出凹點踢除】
        /// 
        /// 
        /// 
        public List s_convex_polyon2(List gSur_Point_list)
        {
            Stack StackPoint = new Stack();
            var isCCW = s_isCCW(gSur_Point_list);
            int sum = gSur_Point_list.Count() - 1;
            int n = gSur_Point_list.Count();
            for (int i = 0; i < n; i++)
            {
                int IndexPre = (i - 1) % sum;
                if (IndexPre == -1) IndexPre = sum - 1;
                int IndexCurrent = i % sum;
                int IndexNext = (i + 1) % sum;
                if (gSur_Point_list[IndexPre].type_point > 0) continue;
                if (gSur_Point_list[IndexCurrent].type_point > 0) continue;
                var multiVal = multi(gSur_Point_list[IndexPre].p, gSur_Point_list[IndexCurrent].p, gSur_Point_list[IndexNext].p);
                if ((isCCW && multiVal > 0) || (!isCCW && multiVal < 0))
                {
                    L1:
                    if (StackPoint.Count > 1)
                    {
                        var Top1Point = StackPoint.Pop();
                        var Top2Point = StackPoint.Peek();
                        multiVal = multi(Top2Point.p, Top1Point.p, gSur_Point_list[IndexCurrent].p);
                        if ((isCCW && multiVal > 0) || (!isCCW && multiVal < 0))
                            StackPoint.Push(Top1Point);
                        else
                            goto L1;   
                    }
                    StackPoint.Push(gSur_Point_list[IndexCurrent]);
                }
            }
            return StackPoint.Reverse().ToList();
        }

方法三求凸包:【按算法導論Graham掃描法 各節點按方位角+距離 逆時針排序 依次檢查,當不屬凸點于則彈出】

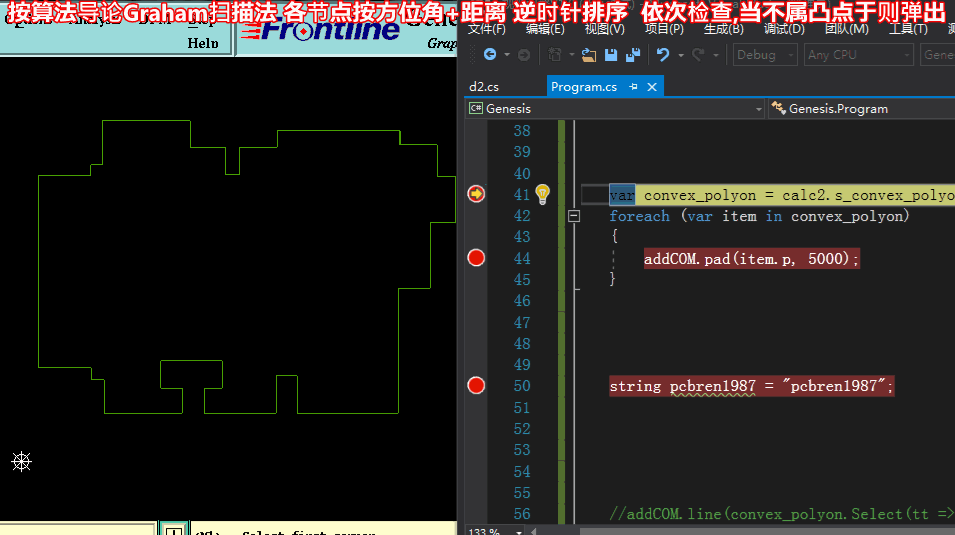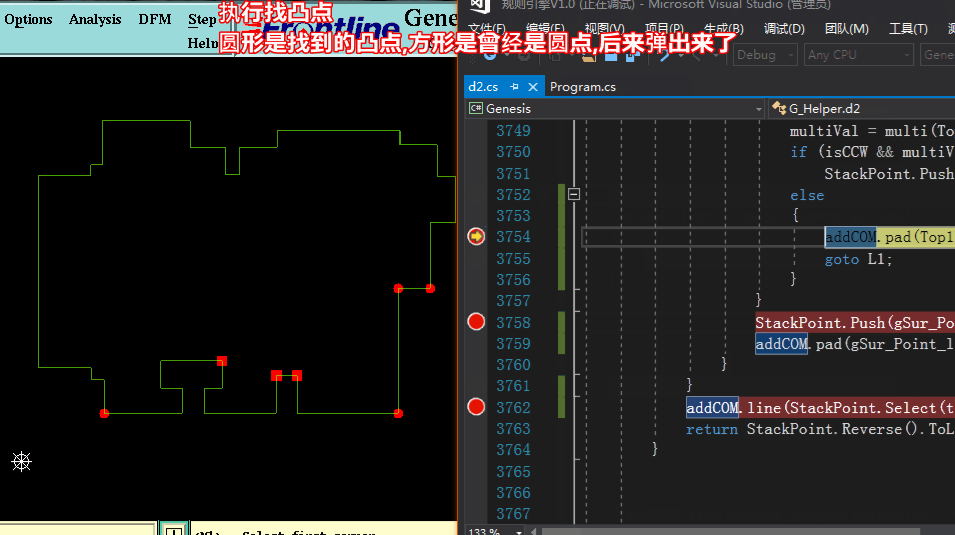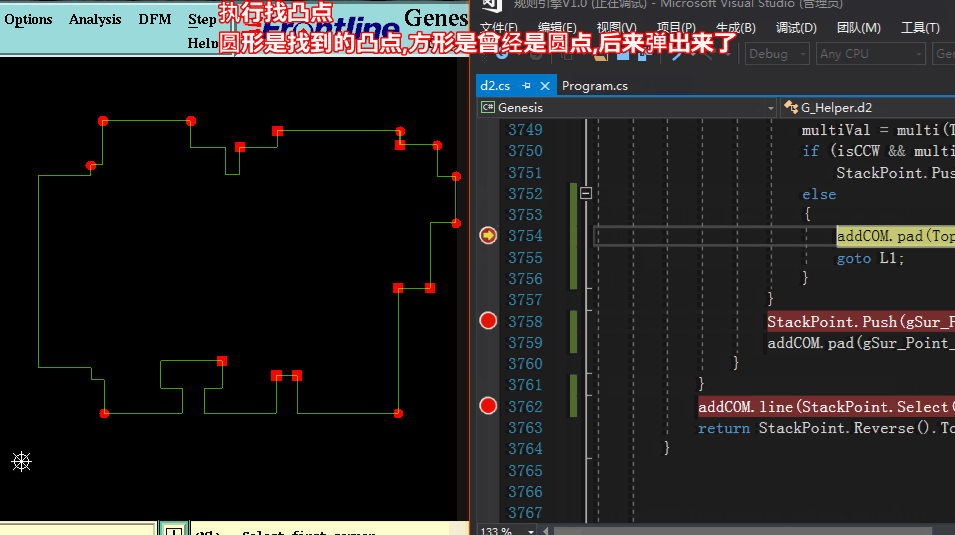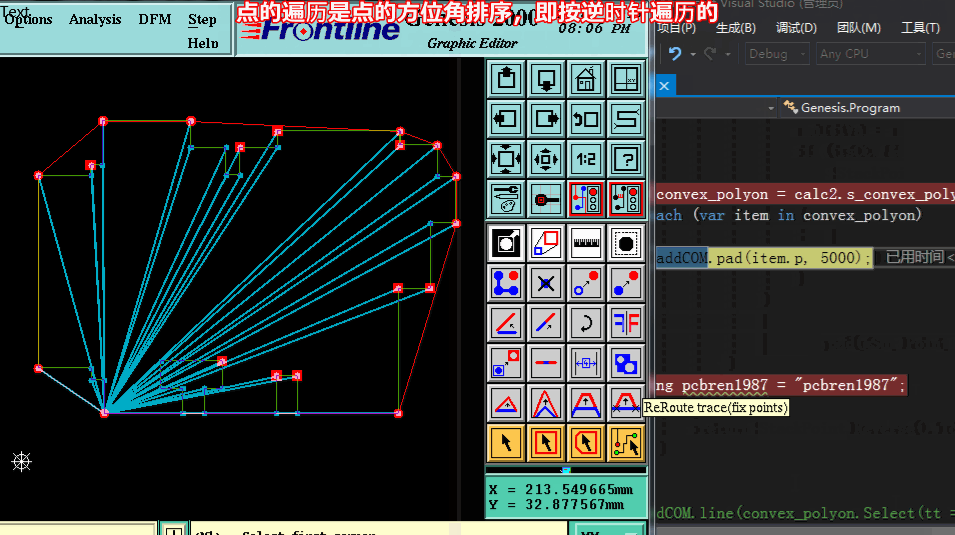
方法三求凸包代碼

        /// 

        /// 求最大多邊形最大凸包5  【按算法導論Graham掃描法 各節點按方位角+距離 逆時針排序  依次檢查,當不屬凸點于則彈出】
        /// 由于把各點的排列順序重新排序了，只支持折線節點(當存在弧節點時會出異常 ！！！)
        /// 
        /// 
        /// 
        public List s_convex_polyon3(List gSur_Point_list)
        {
            var LeftBottomPoint = gSur_Point_list.OrderBy(tt => tt.p.y).ThenBy(tt => tt.p.x).FirstOrDefault();
            gSur_Point_list.RemoveAt(gSur_Point_list.Count - 1);
            gSur_Point_list.ForEach(tt =>
                                        {
                                            tt.Value = p2p_di(LeftBottomPoint.p, tt.p);
                                            tt.Angle = p_ang(LeftBottomPoint.p, tt.p);
                                        }
                );
            gSur_Point_list = gSur_Point_list.OrderBy(tt => tt.Angle).ThenBy(tt => tt.Value).ToList();
            gSur_Point_list.Add(gSur_Point_list[0]);
            Stack StackPoint = new Stack();
            var isCCW = true;
            int sum = gSur_Point_list.Count() - 1;
            int n = gSur_Point_list.Count();
            for (int i = 0; i < n; i++)
            {
                int IndexPre = (i - 1) % sum;
                if (IndexPre == -1) IndexPre = sum - 1;
                int IndexCurrent = i % sum;
                int IndexNext = (i + 1) % sum;
                var multiVal = multi(gSur_Point_list[IndexPre].p, gSur_Point_list[IndexCurrent].p, gSur_Point_list[IndexNext].p);
                if (isCCW && multiVal > 0)
                {
                    L1:
                    if (StackPoint.Count > 1)
                    {
                        var Top1Point = StackPoint.Pop();
                        var Top2Point = StackPoint.Peek();
                        multiVal = multi(Top2Point.p, Top1Point.p, gSur_Point_list[IndexCurrent].p);
                        if (isCCW && multiVal > 0)
                            StackPoint.Push(Top1Point);
                        else
                            goto L1;
                    }
                    StackPoint.Push(gSur_Point_list[IndexCurrent]);
                }
            }
            return StackPoint.Reverse().ToList();
        }

公共方法與數據結構

?View Code

三.板邊凸點倒圓角方法

方法一：也最簡單的倒角方法,我們將PCB板邊凸點找出來后，可以直接借助genesis倒角功能就可以實現了

當然但偶爾會報錯的, 且當N個小線段組成的尖角倒角會出錯(要實現完美效果只有自己寫倒角算法啦)

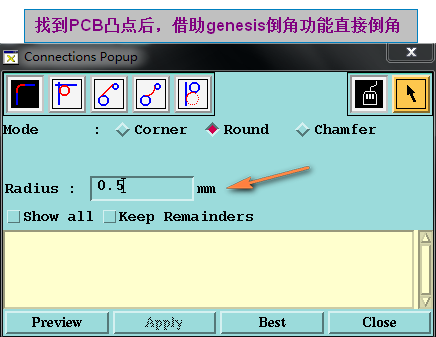
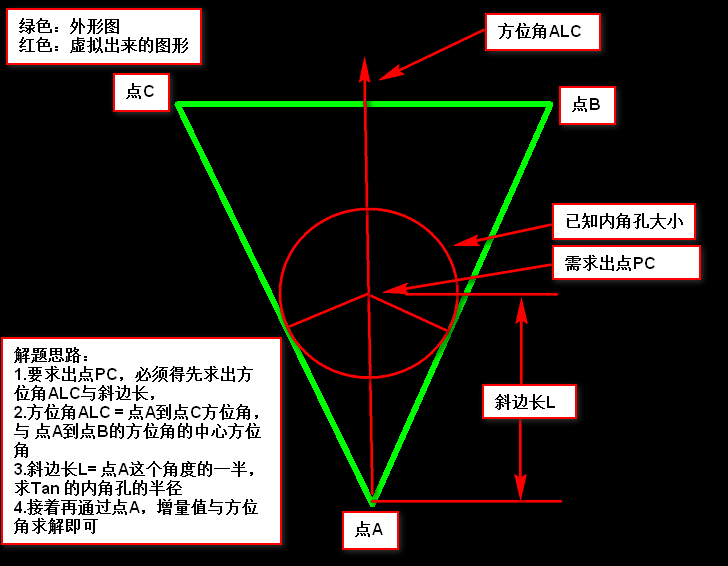
方法二:自己寫倒角算法，這個算法和加內角孔算法類似（這里只是介紹簡單的倒角)考慮特殊的需要擴展

可以參考這篇文章:https://www.cnblogs.com/pcbren/p/9665304.html

四.凸點加倒圓角實現效果

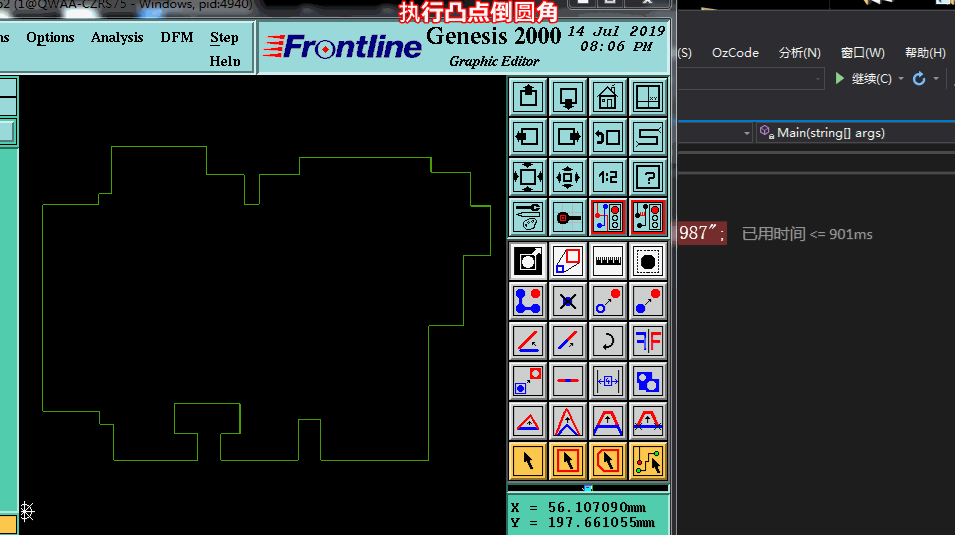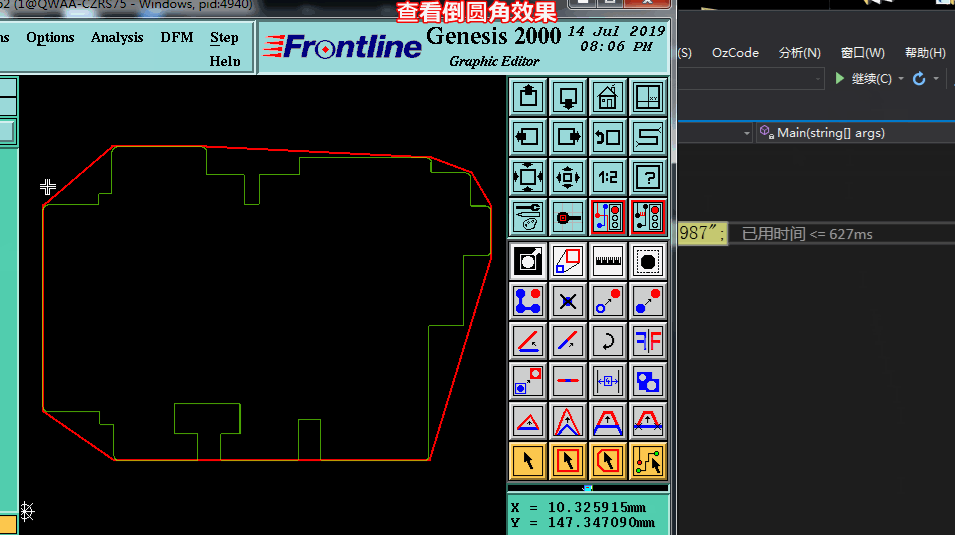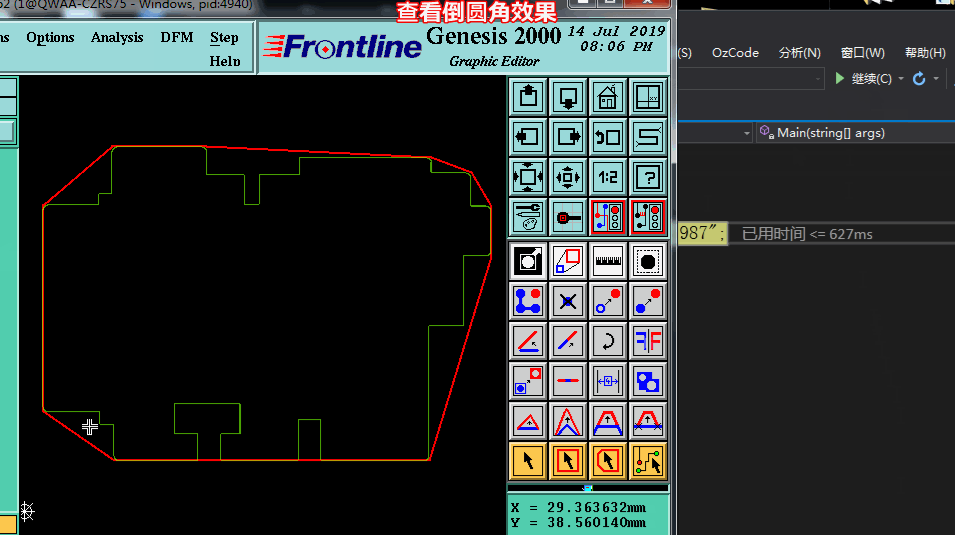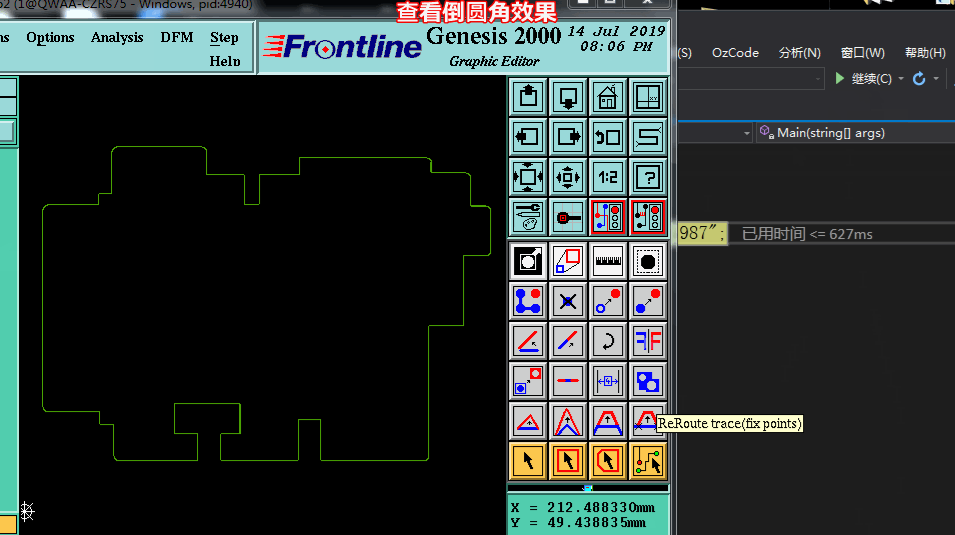
——End——

審核編輯 ：李倩