在本文中，我們將討論一些基本的信號運算，將其中一個信號視為常數值。

信號可以在數學上表示參數的變化。

如果信號的值隨時間發生一致的變化，那么我們就會得到一個交變信號。另一方面，如果信號的值在很寬的范圍內保持恒定，那么我們得到一個恒定值的信號。這些概念分別用交流電 （AC）和直流電 （DC） 來說明。

我們在這些文章中的示例信號隨時間不斷變化。本質上，我們沒有處理恒定值信號。

然而，在本文中，我們將回顧與之前相同的基本信號操作，但我們將使用常數值信號作為示例。

具有恒定值信號的交流信號的加法/減法

添加信號：正鉗位

讓我們從圖 1 中紅色曲線所示的正弦信號開始。

現在，讓我們添加一個幅度為 1.5 的恒定值信號。我們的輸出信號變為y（t） = x（t） + 1.5。獲得的圖由同一圖中的藍色曲線表示。

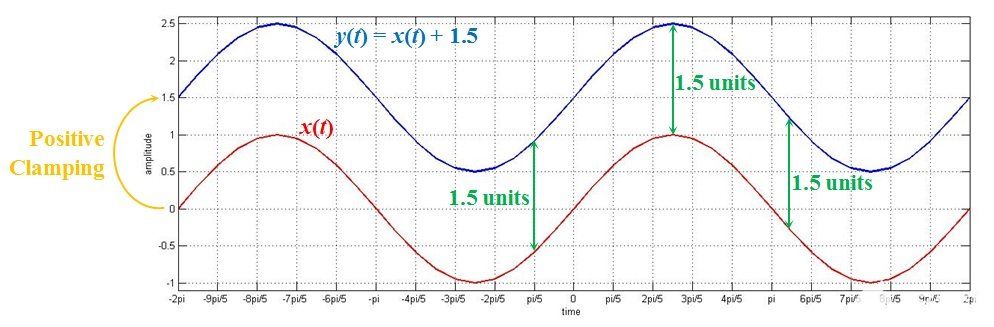
圖 1. 將交流信號與幅度為 1.5 的恒定值信號相加

如您所見， y（t） 與 x（t） 相同，但沿其軌跡移動了 1.5 的幅度（添加到它的常數值）。

這很好地說明了當我們將恒定值信號添加到交流信號時會發生什么——后者轉移到前者的水平。交流信號的參考電平的這種變化稱為“鉗位”。因為，在這個例子中，有一個向正值的轉變，我們可以稱之為“正鉗位”。

如果我們將交流信號添加到恒定值信號中會發生什么？該數學方程將是y（t） = 1.5 + x（t）。

但是，結果將是相同的。為什么？與簡單的數學一樣，加法是可交換的，這意味著 x（t） + 1.5 = 1.5 + x（t）。

減法信號：負鉗位

接下來，讓我們嘗試減法。我們將從交流信號中減去我們的示例恒定值信號開始。設 y（t） 為 x（t） - 1.5。

與此對應的輸出如圖 2 中的藍色曲線所示。通過將該曲線與代表原始信號的紅色曲線進行比較，我們可以看到信號的幅度總體上降低了 1.5。

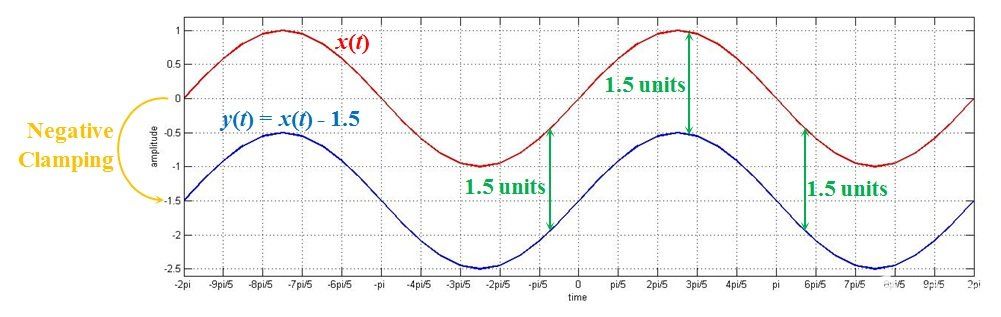
圖 2.從交流信號中減去幅度為 1.5 的恒定值信號的效果

從圖中可以明顯看出，這樣做的直接后果是將交流信號鉗位到 -1.5。由于鉗位朝向負值，我們稱其為“負鉗位”。

當我們將其寫為 y（t） = x（t） - 1.5 為 y（t） = - 1.5 + x（t） 時，我們可以看到，即使在這種情況下，也必須發生鉗位，但趨向于負值。

作為延續，現在讓我們嘗試顛倒減法的順序。也就是說，讓我們的輸出信號為 y（t） = 1.5 - x（t） 而不是 y（t） = x（t） - 1.5。

圖 3 顯示了與此操作對應的結果：

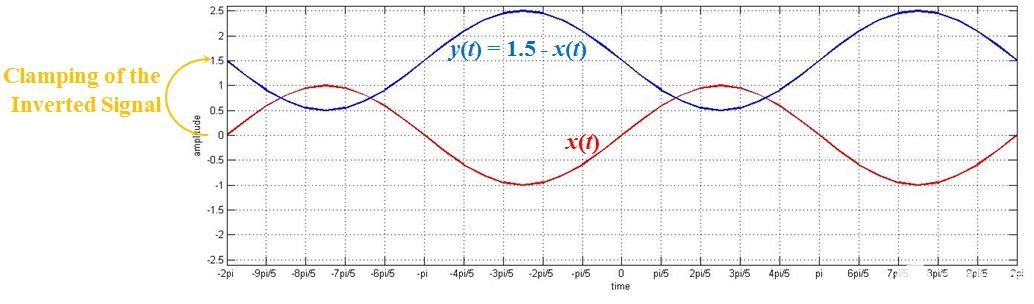
圖 3.從幅度為 1.5 的恒定值信號中減去交流信號的效果

乍一看，這似乎把我們“夾住”的想法拋到了窗外。然而，這并不完全正確。

為什么？

仔細觀察。圖中的藍色曲線是交變信號，但沿水平軸反轉并鉗制在 1.5 水平。

在這種情況下，我們的輸出方程是 y（t） = 1.5 - x（t），這與 y（t） = 1.5 + {-x（t）} 相同。這表明，在這里，倒置的 x（t） 應該被限制在 1.5 的水平。

關于加法或減法的結論

我們可以得出結論，恒定值信號與交替信號相加或相減總是會導致將交替信號鉗位到由常數決定的值。

從電子學上講，產生鉗位的電路稱為“鉗位器”。

所以我們知道，在其中至少一個是常數值的信號中執行的加法/減法運算可以在所有應用鉗位器的場景中找到它們的用途。基線穩定器、直流恢復電路以及用于在設備的工作范圍與輸入信號的工作范圍之間建立兼容性的電路只是您可能會看到這些操作的幾個應用示例。

將恒定值信號與交流信號相乘的效果

在本節中，我們將研究將恒定值信號與交替信號相乘的效果。特別是，讓我們將幅度為 1.5 的恒定值信號與交變信號x（t） 相乘，它是周期為 2π 的正弦波（如圖 4 中的紅色曲線所示）。

結果圖在圖 4 中顯示為藍色曲線：

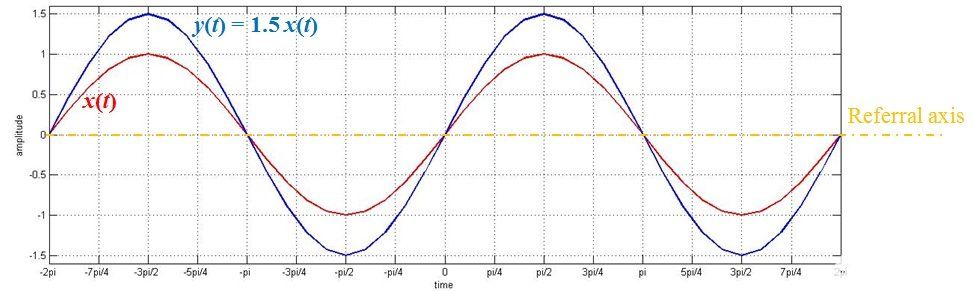
圖 4.幅度為 1.5 的恒定值信號乘以交流信號

從圖中可以看出， x（t） 在 –π/2 處的值為 -1，而 y（t） 的值為 -1.5（即 x（t） 值的 1.5 倍）。類似地，在時刻 0、π/2 和 3π/2，我們的 y（t） 值分別為 0、1.5 和 -1.5。您會注意到這些是 x（t）（分別為 0、1 和 -1）乘以 1.5 的值。

這表明，當我們將一個信號乘以一個常數值時，我們得到一個信號，其值乘以相同的因子。

在這一點上，我們應該討論與圖 4 相關的一個重要點。與加法和減法不同（如圖 1 到圖 3 所示），乘法運算不會導致信號鉗位。然而，與加法一樣，乘法是可交換的，得到y（t） = 1.5 x（t） = x（t） 1.5。

關于乘法的結論

從上面的討論中可以清楚地看出，一個信號與一個大于 1 的常數相乘會增加其幅度，而不會對其進行鉗位。這本質上是將輸入信號放大了一個由常數值決定的因子。因此，這種乘法運算在所有使用電子放大器的情況下都有用。

這方面的一些示例應用是通信系統中的低噪聲放大器、無線電/電視機的音頻/視頻放大器以及構成眾多電子電路的組成部分的運算放大器。

定值信號的微分和積分

根據數學，常數的微分將為零。即使在信號的情況下也是如此。也就是說，通過對一個常數值信號進行微分，我們將得到一個零值信號。這是許多電子設計中使用的隔直電容器工作背后的工作原理。

另一方面，如果我們對一個常數值信號進行積分，我們會得到一個斜率，其斜率由常數值決定。像恒流斜坡發生器這樣的電路就是根據這個原理工作的。

概括

在本文中，我們分析了將恒定值信號應用于基本信號運算時產生的結果。我們還看到了加法/減法、乘法、微分和積分等運算如何分別產生鉗位、放大、直流阻斷和斜坡生成等效果。