53. 最大子序和

力扣題目鏈接：https://leetcode-cn.com/problems/maximum-subarray

給定一個整數數組 nums ，找到一個具有最大和的連續子數組（子數組最少包含一個元素），返回其最大和。

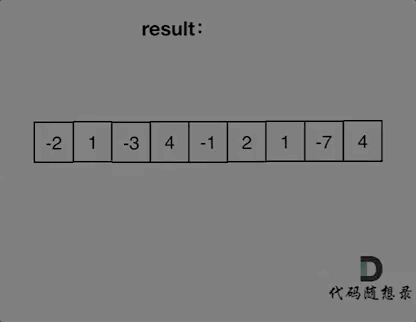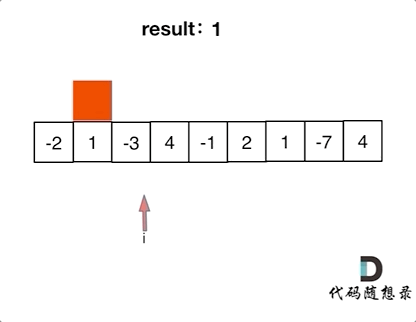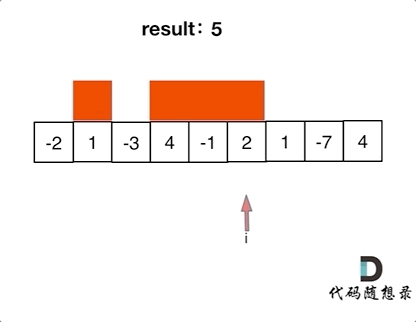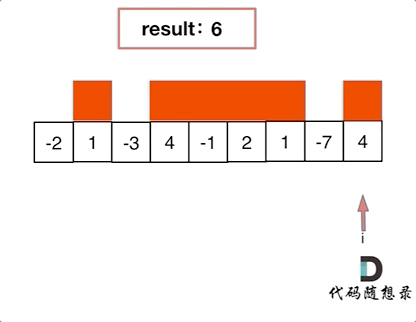
示例: 輸入: [-2,1,-3,4,-1,2,1,-5,4] 輸出: 6 解釋:連續子數組[4,-1,2,1] 的和最大，為 6。

暴力解法

暴力解法的思路，第一層for 就是設置起始位置，第二層for循環遍歷數組尋找最大值

時間復雜度：O(n^2) 空間復雜度：O(1)

classSolution{
public:
intmaxSubArray(vector<int>&nums){
intresult=INT32_MIN;
intcount=0;
for(inti=0;i//設置起始位置
count=0;
for(intj=i;j//每次從起始位置i開始遍歷尋找最大值
count+=nums[j];
result=count>result?count:result;
}
}
returnresult;
}
};

以上暴力的解法C++勉強可以過，其他語言就不確定了。

貪心解法

貪心貪的是哪里呢？

如果 -2 1 在一起，計算起點的時候，一定是從1開始計算，因為負數只會拉低總和，這就是貪心貪的地方！

局部最優：當前“連續和”為負數的時候立刻放棄，從下一個元素重新計算“連續和”，因為負數加上下一個元素 “連續和”只會越來越小。

全局最優：選取最大“連續和”

局部最優的情況下，并記錄最大的“連續和”，可以推出全局最優。

從代碼角度上來講：遍歷nums，從頭開始用count累積，如果count一旦加上nums[i]變為負數，那么就應該從nums[i+1]開始從0累積count了，因為已經變為負數的count，只會拖累總和。

這相當于是暴力解法中的不斷調整最大子序和區間的起始位置。

那有同學問了，區間終止位置不用調整么？如何才能得到最大“連續和”呢？

區間的終止位置，其實就是如果count取到最大值了，及時記錄下來了。例如如下代碼：

if(count>result)result=count;

這樣相當于是用result記錄最大子序和區間和（變相的算是調整了終止位置）。

如動畫所示：

紅色的起始位置就是貪心每次取count為正數的時候，開始一個區間的統計。

那么不難寫出如下C++代碼（關鍵地方已經注釋）

classSolution{
public:
intmaxSubArray(vector<int>&nums){
intresult=INT32_MIN;
intcount=0;
for(inti=0;iif(count>result){//取區間累計的最大值（相當于不斷確定最大子序終止位置）
result=count;
}
if(count<=?0)count=0;//相當于重置最大子序起始位置，因為遇到負數一定是拉低總和
}
returnresult;
}
};

時間復雜度：O(n) 空間復雜度：O(1)

當然題目沒有說如果數組為空，應該返回什么，所以數組為空的話返回啥都可以了。

不少同學認為 如果輸入用例都是-1，或者 都是負數，這個貪心算法跑出來的結果是0， 這是又一次證明腦洞模擬不靠譜的經典案例，建議大家把代碼運行一下試一試，就知道了，也會理解 為什么 result 要初始化為最小負數了。

動態規劃

當然本題還可以用動態規劃來做，當前「代碼隨想錄」主要講解貪心系列，后續到動態規劃系列的時候會詳細講解本題的dp方法。

那么先給出我的dp代碼如下，有時間的錄友可以提前做一做：

classSolution{
public:
intmaxSubArray(vector<int>&nums){
if(nums.size()==0)return0;
vector<int>dp(nums.size(),0);//dp[i]表示包括i之前的最大連續子序列和
dp[0]=nums[0];
intresult=dp[0];
for(inti=1;i1]+nums[i],nums[i]);//狀態轉移公式
if(dp[i]>result)result=dp[i];//result保存dp[i]的最大值
}
returnresult;
}
};

時間復雜度：O(n) 空間復雜度：O(n)

總結

本題的貪心思路其實并不好想，這也進一步驗證了，別看貪心理論很直白，有時候看似是常識，但貪心的題目一點都不簡單！

后續將介紹的貪心題目都挺難的，哈哈，所以貪心很有意思，別小看貪心！

其他語言版本

Java

classSolution{
publicintmaxSubArray(int[]nums){
if(nums.length==1){
returnnums[0];
}
intsum=Integer.MIN_VALUE;
intcount=0;
for(inti=0;i//取區間累計的最大值（相當于不斷確定最大子序終止位置）
if(count<=?0){
count=0;//相當于重置最大子序起始位置，因為遇到負數一定是拉低總和
}
}
returnsum;
}
}

//DP方法
classSolution{
publicintmaxSubArray(int[]nums){
intans=Integer.MIN_VALUE;
int[]dp=newint[nums.length];
dp[0]=nums[0];
ans=dp[0];

for(inti=1;i1]+nums[i],nums[i]);
ans=Math.max(dp[i],ans);
}

returnans;
}
}

Python

classSolution:
defmaxSubArray(self,nums:List[int])->int:
result=-float('inf')
count=0
foriinrange(len(nums)):
count+=nums[i]
ifcount>result:
result=count
ifcount<=?0:
count=0
returnresult

Go

funcmaxSubArray(nums[]int)int{
maxSum:=nums[0]
fori:=1;ilen(nums);i++{
ifnums[i]+nums[i-1]>nums[i]{
nums[i]+=nums[i-1]
}
ifnums[i]>maxSum{
maxSum=nums[i]
}
}
returnmaxSum
}

審核編輯 ：李倩