一、關于多采樣率數字濾波器

很明顯從字面意思上可以理解，多采樣率嘛，就是有多個采樣率唄。前面所說的FIR，IIR濾波器都是只有一個采樣頻率，是固定不變的采樣率，然而有些情況下需要不同采樣頻率下的信號，具體例子我也不解釋了，我們大學課本上多速率數字信號處理這一章也都舉了不少的例子。

按照傳統的速率轉換理論，我們要實現采樣速率的轉換，可以這樣做，假如有一個有用的正弦波模擬信號，AD采樣速率是f1，現在我需要用到的是采樣頻率是f2的信號，傳統做法是將這個經過f1采樣后的信號進行DA轉換，再將轉換后的模擬信號進行以f2采樣頻率的抽樣，得到采樣率為f2的數字信號，至此完成采樣頻率的轉換

但是這樣的做法不僅麻煩，而且處理不好的話會使信號受到損傷，所以這種思想就被淘汰了，現在我們用到的采樣率轉換的方法就是抽取與內插的思想。

二、抽取

先來總體來解釋一下抽取的含義：前面不是說，一個有用的正弦波模擬信號經采樣頻率為f1的抽樣信號抽樣后得到了數字信號，很明顯這個數字信號序列是在f1頻率下得到的，現在，假如我隔幾個點抽取一個信號，比如就是5吧，我隔5個點抽取一個信號，是不是就是相當于我采用了1/5倍f1的采樣頻率對模擬信號進行采樣了？所以，抽取的過程就是降低抽樣率的過程，但是我們知道，這是在時域的抽樣，時域的抽樣等于信號在頻域波形的周期延拓，周期就是采樣頻率，所以，為了避免在頻域發生頻譜混疊，抽樣定理也是我們要考慮的因素。

下面來具體來介紹

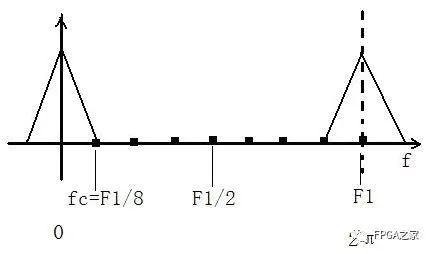
如上圖所示，假如上面就是某一有用信號經采樣頻率f1抽樣得到的頻譜，假設這時候的采樣頻率為8Khz，可以通過數格子得到，從0到F1處有8個空格，每個空格代表1Khz，有些朋友可能會問，這不是在數字頻域嗎，單位不是π嗎，哪來的hz？是的，這里是數字頻域，采樣頻率F1處對應的是2π，這里只是為了好解釋，我們用模擬頻率來對應數字頻率。

上面是采樣頻率為8K的數字信號頻域圖，現在我要對這個數字信號進行時域抽取，從而來降低信號的采樣率，我們知道，一旦我們對數字信號進行時域抽取，那么采樣率下降，而采樣率就是數字信號頻域的波形周期，那么也就是周期下降，所以，我們對信號進行抽取要有個度，要在滿足抽樣定理的條件下對信號進行抽取，否則就會發生頻譜混疊。

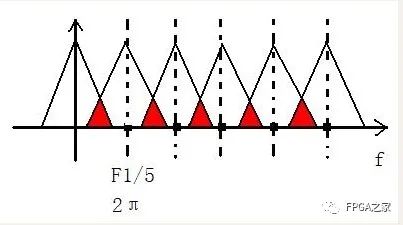
上圖就是對信號進行了1/5倍的F1采樣頻率抽取，可見，由于發生了頻譜混疊現象，因為1/5倍的F1是1600hz，而信號的頻帶是1000hz，不滿足抽樣定理，導致發生了頻譜混疊，所以，為了避免發生這種情況，除了要滿足抽樣定理之外，即抽樣倍數不能太高，我們還需要把信號的頻帶設置在F1/2以下，才能確保信號不發生頻譜混疊，因此，我們需要在抽取之前加一個低通濾波器，書上叫做抗混疊低通濾波器，用來限制信號的頻帶，然后再進行抽取，這樣的話我們來算一下

低通濾波器的截止頻率就是1/2倍的經抽取后的采樣速率，即fc = 1/2 * （F1/M） ，M是抽取倍數。而1/2*F1對應的數域頻率是π，因此我們得出，

抗混疊低通濾波器的截止頻率是π/M

三、內插

抽取的過程是降低采樣率的過程，那么插值的過程當然就是提高采樣率的過程。大體的思路可以這么理解，我們將經f1抽樣下得到的數字信號的每兩個點之間進行插值，插入的值是0，插值之后，信號在單位時間內的采樣點數增多，當然也就是采樣速率的提升，采樣速率提升后我們知道，那么信號的頻譜的周期就會增加。

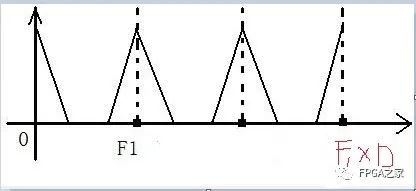
需要注意的一點就是，插值前后，我們只是在時域信號中間插入了D-1個零值，僅僅是改變了采樣率，并沒有改變信號的信息，因此，在頻域，信號頻譜的形狀是不會改變的，改變的僅僅是周期，如上圖，F1是插值之前信號的周期，插值之后，信號頻譜的形狀不變，周期成了F1*D，D是插值倍數。如果我們直接用F1*D倍的采樣率采信號，得到的頻譜會發現，就不會有中間兩個波形，因此，這兩個波形是多余的，書上叫做是鏡像頻譜。既然是多余的，我們就可以將它用一個低通濾波器濾掉，這樣的低通濾波器，就叫做鏡像低通濾波器。這樣我們來計算一下鏡像低通濾波器的截止頻率。

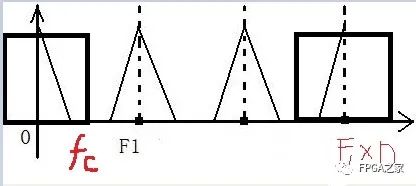
根據上面這張圖我們可以求出鏡像低通濾波器的截止頻率，可以看到，fc = 1/2 *F1,這里我們假設，內插之后的采樣頻率為F2 =F1*D，那么，fc =1/2*(F2/D)，而1/2*F2對應的是π，注意，這里是1/2*F2對應π，不是1/2*F1了，因為這已經是插值之后采樣率增加之后的頻譜了，所以我們得出：

鏡像低通濾波器的截止頻率為：π/D

四、 分數倍抽取與內插

根據前面抽取與內插的介紹我們知道了，內插的過程是先進行內插處理，再通過鏡像低通濾波器，抽取的過程就是先進行抗混疊低通濾波，再進行抽取，我們可以看出來，假如我們想進行分數倍抽取，比如我要進行3/5倍抽取，就可以先進行3倍內插，再進行5倍抽取，這樣就可以實現分數倍抽取。

再來看一下，當進行分數倍抽取與內插的時候，鏡像低通濾波器和抗混疊低通濾波器是連在一起的，因此，我們可以將這兩個濾波器合二為一，截止頻率取兩個濾波器截止頻率的最小值就可以了

五、多速率濾波器的Matlab實現

這里我們假設，要對一個頻率為100hz的正弦波模擬信號進行抽樣，抽樣頻率為900hz，現在我要對采樣信號進行5/3倍提升

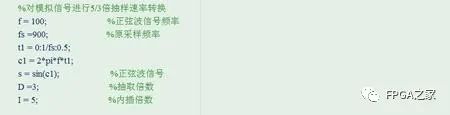
根據我們前面分析的，進行分數倍的抽樣率轉換，先要進行內插處理，內插的過程就是在原有的時域信號之間，插入I- 1個零值點，采用matlab實現很簡單，首先我們可以計算插值完成之后信號的長度，然后將原來信號進行填充即可

插值完成之后，需要進行低通濾波，由前面的討論可以知道，根據低通濾波器的截止頻率計算公式，來計算濾波器截止頻率為π/I，然后調用函數生成FIR濾波器系數即可。

緊接著，需要進行的是抽取處理，抽取過程的算法跟內插類似，可以先計算抽取之后的信號的長度，然后每個D個采樣點進行一次抽取

下面看一張圖，是我繪制了這個過程的整個流程

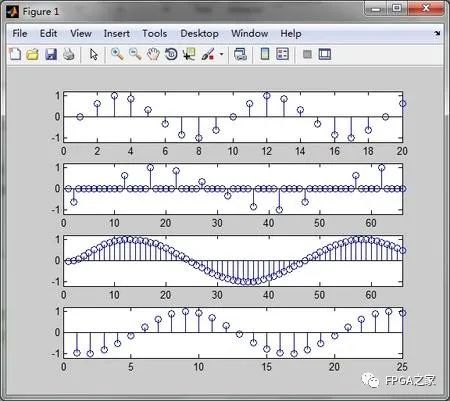
根據上面這張圖我們可以看到，最上面的是原始信號經900hz頻率采樣后得到的信號時域波形，然后我對其進行了5倍內插，也就是在每兩個采樣點之間插入了4個零值，之后通過了低通濾波器，去掉鏡像波形后的時域波形，可以看到，此時的采樣率已經是原來的5倍，接著對其進行3倍抽取，即每隔兩個點抽取一個點作為新的采樣點，得到最下面的時域波形，整個過程原始信號沒有發生變化，變化的僅僅是采樣率。

六、關于CIC濾波器

說了這么多，終于進入正題了。前面的都是些基礎知識，只有先掌握了前面的內容，才能理解下面的知識，包括下兩篇文章要講的FIR半帶濾波器和多相結構的FIR半帶濾波器。

CIC濾波器呢，是積分梳狀濾波器的英文簡稱，先來看CIC濾波器的單位沖擊響應

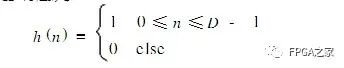
很明顯的一個特征就是，CIC濾波器的單位脈沖響應只有0和1，再來想一下，既然單位脈沖響應只有0和1，那么也就是意味著，我們在進行卷積運算的時候，就不需要乘法器，為什么呢？因為濾波器系數為1的話，相當于將輸入信號乘了個1，所以就不需要乘法器，只需要加法器就可以完成卷積運算，正因為如此，CIC濾波器結構簡單，非常適合工作在高采樣率條件下

但是這并不是我們常用的濾波器結構，既然是積分梳狀濾波器，總得體現一下積分、和梳狀這兩個特點吧，這名字不是白叫的，因此有如下變形

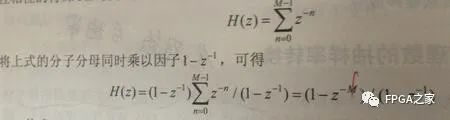
可以看到，上面的式子是CIC濾波器的系統函數，對其進行變換之后可以得到兩個部分的乘積形式，即分子部分為一個梳狀FIR濾波器，剩余部分為一個積分器，至此，我們CIC濾波器的結構才已經成型。

根據變形后的CIC濾波器的系統函數可以知道，濾波器的極點為1，因此看上去濾波器是一個不穩定的系統，但是從整體角度來看，這個結構是由一個FIR濾波器變形而來的，本身是一個因果穩定的，因此，變形后的系統應該也是一個因果穩定的，因此我們考慮到零極點抵消的原因，致使變形后的系統仍是一個因果穩定的系統。

從單級CIC濾波器的幅頻響應考慮，由于其特殊的結構，導致單級CIC濾波器的衰減不足，可以見下圖

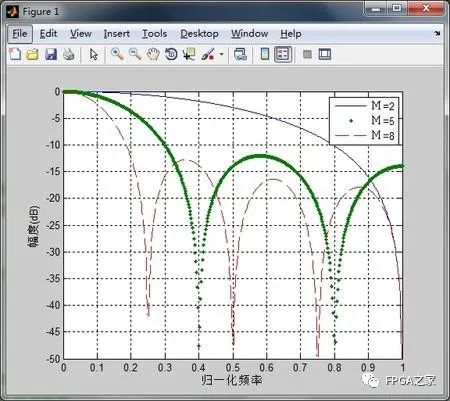
可見，單級CIC濾波器濾波器的衰減并不是很足，在階數比較大的情況下，CIC濾波器的衰減一般穩定在13.6dB，要想加大衰減，就必須采用多級CIC濾波器級聯的形式，每增加一級濾波器，阻帶衰減增加13.6dB，但是為了增加阻帶衰減而采用級聯方式，也會導致一些弊端，為此，這方面的知識總結如下，具體理論不再解釋了，書上的推導過程比較復雜，大家還是自己看書為好。

總結：

1、要同時滿足通帶容限跟阻帶容限的誤差的CIC濾波器實現起來比較困難，因為要想阻帶衰減大，就要增大濾波器級數，但是會導致通帶容限增大。

2、如果要實現這樣的濾波器，只有當有用信號的頻帶相對于采樣信號的速率很小時才能設計出符合要求的濾波器，這樣的話通帶衰減較大的情況下也對有用信號影響較小。

3、有用信號的頻帶相對于采樣信號的速率很小也就是意味著信號的采樣率很高，所以，CIC濾波器適合應用在多速率信號處理的前端，作為抗混疊濾波器來用，或者是作為后端的抗混疊插值濾波器。

七、多級HogenauerCIC抽取濾波器的FPGA實現

HogenauerCIC抽取濾波器是一種特殊的結構，可以用來提高濾波器的運行速度，節省硬件資源等

前面已經說過了，CIC濾波器的系統函數經過變形之后，可以得到一個M階的梳狀濾波器和一個積分器相乘的形式，二者共同組成了抗混疊低通濾波器，在抽取的過程中，一般是信號先經過抗混疊低通濾波器進行濾波，來避免頻譜混疊現象的發生，然后再進行抽取處理，但是我們可以利用Noble恒等式，先對信號進行抽取，再對其進行濾波，即

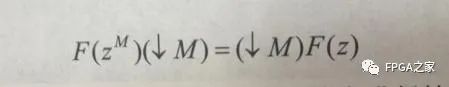
也就是說，在濾波器階數跟抽取倍數相同的情況下，如果先濾波后抽取，那么濾波器的長度是M，但是如果先抽取后濾波，那么濾波器的長度就會降低為1階，因此，采用Noble恒等式，先抽取后濾波，可以降低濾波器長度，從而達到節省硬件資源的目的。

前面說了，單級的CIC濾波器很難滿足需求，要達到一定的阻帶衰減，就必須通過級聯的方式

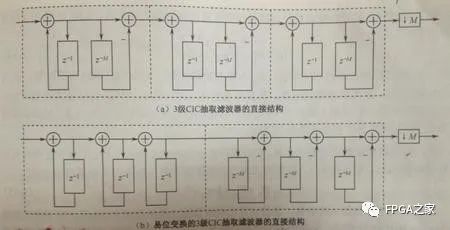
我們可以看到，如果是三級的CICI濾波器級聯的話，也就是有3個積分器和三個梳狀濾波器，這時候我們可以利用Noble恒等式進行移位變換，讓積分器放在一起，梳狀濾波器放在一起，這時候的梳狀濾波器是M階的，因為此時還沒有經過抽取，所以我們可以再利用Noble恒等式，將抽取器放到梳狀濾波器之前，這樣的話，梳狀濾波器就會降為1階，長度為2，從而大大節省了硬件資源

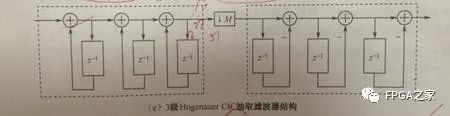
現在我們假設抽取倍數是5，根據要求，這時我們的濾波器長度也應該是5，采用3級CIC濾波器級聯的方式，用HogenauerCIC抽取濾波器結構在FPGA上設計

1、三級積分器模塊

altera 的CIC濾波器的IP核手冊中給出了CIC濾波器中間運算數據字長的計算公式，這里我們假設我們的輸入數據是經過10bit量化過的正弦波數字信號，那么CIC濾波器的中間運算字長為：

Wi = Win+N*log2(MD)

Win是輸入字長為10，N為濾波器長度5，M為抽取倍數5，D位級聯數3

因此算得CIC濾波器的中間字長為 Wi = 10 +5*log2(5*3) =30

知道了我們中間運算的字長就可以來設計我們的模塊了，首先是積分器

積分器的設計比較簡單，就是一個反饋回路，輸出結果跟輸入相加后延時一個時鐘單元后再與輸入相加

剩下兩級積分器也是一樣，第一級積分器的輸出要送到第二級積分器的輸入，代碼這里不再列出，都是跟第一級積分器類似

2、五倍抽取器

抽取器的實現很簡單，從積分器輸出的數據，我們每隔5個數據抽取一個數據就好了

3、三級梳狀濾波器

我們知道，經過抽取之后的梳狀濾波器階數降為1，長度為2的這樣一個FIR濾波器，由于他的頻譜很像一把梳子，因此得名為梳狀濾波器。根據前面的變形后的公式，我們很容易得出，1階梳狀濾波器的單位脈沖響應為hn = 1 ， -1，既然有了單位脈沖響應，我們做的就是一個簡單的卷積運算就好了，而且這里的系數只有1和-1不需要乘法器，做一下加減法就好了

我們可以看到，跟之前做FIR濾波器一樣，我們先把數據送到移位寄存器，因為1階FIR濾波器只有兩個系數，因此只要兩個移位寄存器就夠了。然后我們把系數跟輸入的數據對應相乘，因為系數是1，所以乘法器就省略了，只需要做些加減運算就好了。

經過3級梳狀濾波器濾波后的信號就是我們需要的信號了

然后是關于濾波器輸出信號的數據截尾問題，我們可以通過matlab仿真，看一下輸出數據的最大數據可以用多少位表示來確定輸出數據位寬，如果不想做仿真的話，可以根據altera的CIC濾波器 的IP核手冊中給出了CIC濾波器輸出數據位寬計算公式來算：

即 Wo =Win +log2(N^D)

這里我算出來是17，因此，我們將梳狀濾波器的輸出值進行截低17位處理

仿真的過程我是采用 一個1khz和一個40khz的正弦波信號合成的，用采樣頻率為200Khz對其進行采樣，按照我們上面的設計，濾波器的截止頻率應該是

fc= 1/2 * (200 / 5) = 20Khz

所以經濾波器濾波后，40Khz的高頻信號將會被濾掉，下面是仿真結果

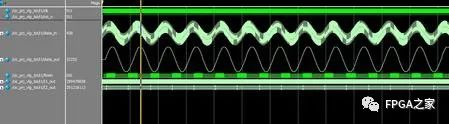
接著，我們將FPGA的輸出信號讀到matlab中進行仿真，繪出輸出信號的時域波形

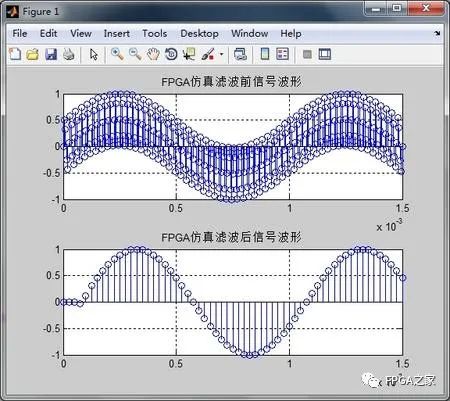
從這張圖我們可以清楚的看到，上面的波形是濾波前的合成信號的波形，下面的是經過濾波后的波形，很明顯，濾波前后，信號的頻率沒有發生改變，發生改變的是采樣率，可以數一下，下面波形兩點之間的距離，要比上面的信號寬4倍，也就是5倍抽取，仿真結果證明，我們的設計是正確的。

原文標題：CIC濾波器的FPGA實現

文章出處：【微信公眾號：FPGA之家】歡迎添加關注！文章轉載請注明出處。

審核編輯：湯梓紅