前文中,我們介紹了一些傳統計算機視覺的算法,包括降噪濾波、二值化、縮放、銳化等,最終我們在FPGA上實現了實時的運動目標跟蹤算法。近些年基于神經網絡的機器學習已經成熟應用于很多商業、工業領域,包括自動駕駛、自動生產,智能醫療等。
那么,作為一本圖像處理的入門教材,除了介紹一些傳統入門的計算機視覺算法與對應的硬件實現,我們也希望引入最近很流行的神經網絡相關的介紹。本章我們將簡單介紹卷積神經網絡和基于LeNet5實現的手寫字符識別,并且在FPGA上實現實時識別的Demo。
一、神經網絡的介紹
1.1人工神經網絡
人工神經網絡(Artificial Neural Networks,簡稱ANN),是受生物神經網絡所啟發而構建的數學模型,去模擬神經元的動作和神經元之間的聯結[1]。一個簡單的人工神經網絡的計算模型如圖1所示。通常一個人工神經網絡包含一個輸入層,不少于一個的隱藏層和一個輸出層。輸入層是由一系列的神經元來接受不同的輸入;隱藏層是介于輸入層和輸出層之間的由一層或者多層神經元和連接組成的。通常隱藏層的數量決定了人工神經網絡的學習和泛化能力。輸出層是輸入經由整個神經網絡學習和分析得到的高層語義結果,比如目標類型等。
圖1(a)所示的人工神經網絡也稱為感知機(Perception),含有多層隱藏層的人工神經網絡為多層感知機(Multi-layer perception)。
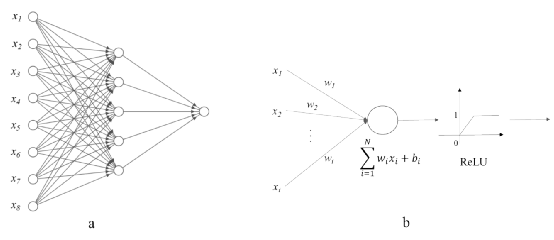
圖 1 一個簡單人工神經網絡的圖表展示(a)展示了一個有8個輸入神經元,一個隱藏層和一個輸出神經元的人工神經網絡,(b)展示了在隱藏層中的一個神經元的數學模型,包含累積和激活函數。
如圖1(b)所示,隱藏層對所有的輸入做加權累積,權重wi反映了不同神經元之間連接的強弱程度,而偏置bi反映了神經元被激活的難易程度。人工神經網絡中的激活函數模擬了生物神經網絡中神經元的調節器,用來控制神經元的興奮和靜息狀態。單個神經元的數學模型hn如下所示:

該公式中,xi是第n個神經元的輸入,wni是第i個輸入xi對應連接的權重,bn 是第n個的神經元的偏置,φ( )是激活函數,如圖1(b)所示,這里用線性整流函數(Rectified Linear Unit)作為激活函數。
1.2卷積神經網絡
卷積層是由一系列并行的卷積核(Kernel)組成,通過對輸入圖像以一定的步長(Stride)進行滑動卷積計算,產生對應的特征圖(Feature map),供下一層計算使用。卷積核通常是二維,也有單個點,一維或者三維的。一個典型的卷積核計算公式如下所示:
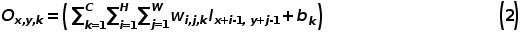
該公式中,Ix,y是第k個卷積核的輸入,wi,j,k是第k個輸入xx,y對應連接的權重,bk 是第k個卷積核的偏置,x, y分別是輸入圖像像素點水平和豎直方向上的位置。i,j分別是權重在水平和豎直方向上的索引(Indices)。
池化層是一個在卷積神經網絡中常見的操作層,主要有兩個作用,一是用來降低維度和計算量。一般卷積計算(步長為1)并不減少維度,而池化層主要是對一定的區域求取最大值或者取均值,這樣的操作分別為最大池化(Max pooling)和平均池化(Average pooling),如圖2所示,為一個示例展示了平均池化和最大池化分別作用于2×2的區域以2的步長滑動。左邊的平均池化是對2 x 2的塊內計算平均值,右邊的最大池化是對2 x 2的塊內尋找最大值。
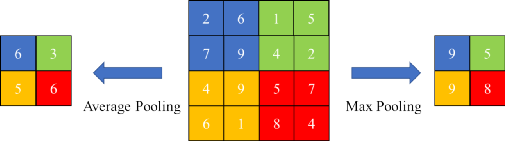
圖 2 2×2平均池化與最大值池化
池化層的另一個作用是盡可能多的保存最有效信息。因為經過卷積計算,圖像中的物體特征可以被精確地提取出來,但是并非所有的特征都是有效的,池化操作可以保留最有效的信息,同時降低了卷積神經網絡對精確特征的敏感度。
批正則化是由Google在2015年提出的[4],目的是為了加速模型收斂,解決內部協變量平移(Internal covariate shift)以及對模型引入正則化。在訓練CNN的過程中,由于數據集太大,我們通常只會將一部分數據(mini-batch)放到CPU或者GPU上。批正則化就是對mini-batch的數據都做正則化,轉換到均值為0,標準差為1的正態分布。批正則化的具體公式見圖3。批正則化的核心思想就是將數據分布變得比較均勻,這樣可以穩定梯度,而且讓每一層的學習率變化沒那么大。CNN的每一層的均值和標準差都是不一樣的,這樣可以等效為引入一定的噪聲,增加了CNN的正則化效果。

圖 3 批正則化的具體算法[4]
在人工神經網絡中提到的激活函數,是作為一個部件來決定在神經元內的信息通路。從生物學上來說,神經元之間通常由電化學來進行信息傳遞的。一般神經元會接收到不同來源的電勢,如果一個神經元達到了興奮電勢,這個神經元將會產生動作電位,把信息通過神經傳遞物質或者電勢傳遞給其相鄰的神經元。反之,如果一個神經元沒有達到興奮電勢,那么它將不能激活也不能傳遞信息。許多種數學模型用來模擬這個生物特征。S型函數(Sigmoid function)是一個比較常見的激活函數,在人工神經網絡和卷積神經網絡中使用的比較多,其公式如下:

該公式中,x是激活函數的輸入。f(·) 是S型函數,將輸出限制在0到1之間(0,1)。S型函數通常用在卷積神經網絡的輸出層,但是該函數在卷積神經網絡優化過程中,有兩個問題。第一個是當S型函數的輸入趨于無窮大時,在反向傳播過程中,梯度會趨近于0,產生了梯度彌散問題,導致卷積神經網絡無法正常收斂。第二個問題是S型函數中的指數和除法運算都會消耗比較多的硬件計算資源。前文提到的線性整流函數(ReLU)也是一個在卷積神經網絡中常用的激活函數。該函數實現簡單,同時又能避免S型函數在反向傳播中容易出現梯度消失的問題。它的導數是0或者1,不會消耗較多的計算資源同時也很容易收斂。其公式如下:

在神經網絡發展的幾十年內,有非常多的理論和應用涌現。本文受限于篇幅,只介紹了基本概念和基礎知識。本文只介紹了標準卷積和常用的激活函數,還有很多其他的卷積類型,比如深度卷積(Depthwise convolution),分組卷積(Group convolution),空洞卷積(Dilated convolution),可變性卷積(Deformable convolution)等。激活函數除了S型函數和線性整流函數,還有tanh函數,Leaky ReLU函數,Swish函數等。接下來,筆者會介紹一個基礎且經典的卷積神經網絡LeNet5,在手寫字符識別中的具體應用以及軟硬件實現。
二、基于LeNet5 CNN的Matlab的實現
2.1 LeNet5 CNN簡介
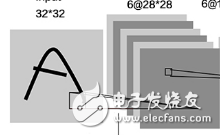
LeNet5卷積神經網絡最早出現在由Yann LeCun等人于1998年發表在Proceedings of The IEEE學術期刊上的“Graident-based Learning Applied to Document Recognition”這篇文章里[5],用于做手寫數字識別(Handwritten digit recognition)。LeNet5卷積神經網絡的結構非常簡單,如圖4所示,其中圖中的灰色方塊代表了一個特征圖。
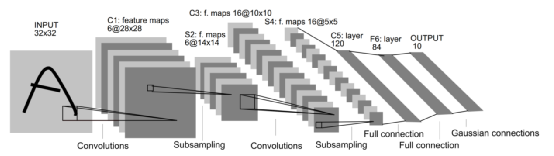
圖 4 LeNet5卷積神經網絡的架構[5]
LeNet5卷積神經網絡有3個卷積層(C1,C3,C5),2個池化層(S2,S4)和2個全連接層(F6和OUTPUT)。LeNet5卷積神經網絡的輸入是分辨率為32×32的灰度圖,所以通道(Channel)數是1。第一層卷積層是由5×5×6的卷積核組成,與輸入層進行卷積操作,我們得到28×28×6的特征圖,即圖4中的C1。經過2×2的平均池化,我們得到14×14×6的特征圖,即圖4中的S2。然后對S2的特征圖進行5×5×16的卷積計算,我們得到10×10×16的特征圖,即圖4中的C3。后面繼續進行池化操作,我們得到5×5×16的特征圖,即圖4中的S4。最后一層卷積層有5×5×120個卷積核。經卷積計算,我們得到1×1×120的特征圖,即圖4中的C5。經過兩個全連接層,我們最終得到1×1×10的輸出,分別對應0-9每個數字的置信度。LeNet5卷積神經網絡的結構如表1所示。LeNet5卷積神經網絡的參數量大約為60,000左右。
表 1 LeNet5卷積神經網絡架構
|
層 |
通道數 |
濾波器大小 |
步長 |
特征圖大小 |
參數量 |
|
輸入層 |
1 |
32×32×1 |
|||
|
卷積層1 |
6 |
5×5 |
1 |
28×28×6 |
5×5×6 + 6 |
|
池化層1 |
2×2 |
2 |
14×14×6 |
||
|
卷積層2 |
16 |
5×5 |
1 |
10×10×16 |
5×5×6×16 + 16 |
|
池化層2 |
2×2 |
2 |
5×5×16 |
||
|
卷積層3 |
120 |
5×5 |
1 |
1×1×120 |
5×5×16×120 + 120 |
|
全連接層1 |
84 |
1×1 |
1×1×84 |
1×1×120×84 + 84 |
|
|
全連接層2 |
10 |
1×1 |
1×1×10 |
1×1×84×10 + 10 |
2.2LeNet5 CNN的Matlab實現
首先我們需要準備MNIST的手寫數字數據集,從[6]上下載。該數據集中有60,000個訓練數據和對應的標簽(Label),還有10,000個測試數據和對應的標簽。數據集圖片和標簽的讀入格式如下圖5,6所示。數據集圖片的像素是按照逐行排列的,像素點值是0-255,0代表白色,255代表黑色,標簽是0-9。
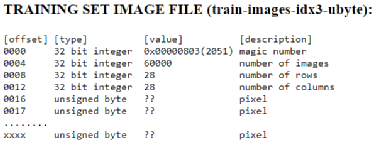
圖 5數據集圖片讀入格式[6]
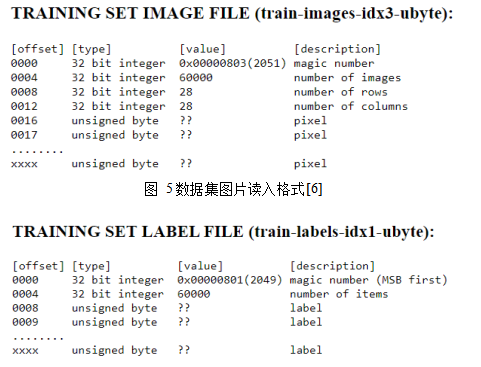
圖 6 標簽讀入格式[6]
在Matlab中,我們將編寫讀MNIST數據集的函數來準備好訓練集和測試集圖片及對應的標簽。具體代碼見loadMNIST.m。


圖 7 a)Matlab中讀入的手寫數字和b)對應的數值
接下來我們將繼續構建LeNet5卷積神經網絡所需的其他部件,比如卷積層,池化層,激活函數和全連接層。卷積層的輸入為H×W×C大小的圖像,卷積核為N×Hin×Win×C的一組濾波器,輸出為Hout×Wout×N的圖像,卷積層還有一個步長參數stride。具體實現代碼見Conv2D.m。

對于池化層,沒有實現論文中的平均池化,我們這里用最大池化來做,平均池化的實現比較類似,讀者有興趣可以自己實現。池化層的輸入為H×W×C大小的特征圖,輸出為(H/Stride)×(W/Stride)×C大小的特征圖,只有一個步長參數。具體實現代碼見Maxpool.m。

我們選擇用ReLU作為激活函數,方便硬件實現。在Matlab中,我們也利用其向量運算的特性來快速實現ReLU函數,具體代碼見ReLU.m。

全連接層就是特殊的卷積層,其卷積核的H和W為1,且輸入的H和W為1。所以這里我們復用了Conv2D的代碼,不再具體展示了。
現在有非常多好用的平臺進行神經網絡的訓練和部署,筆者參考了Matlab來訓練LeNet5卷積神經網絡的,就不詳述在Matlab上實現LeNet5卷積神經網絡的訓練過程了(此部分包含誤差的計算和反向傳遞,權值的更新)。有興趣的讀者可以在網上搜索相關的資料進一步理解。這里我們將TensorFlow訓練的模型導出,然后在Matlab中讀入,對測試集進行推理。如下圖8所示,我們將每一層的結果展示出來,方便我們理解LeNet5卷積神經網絡的特征提取過程。
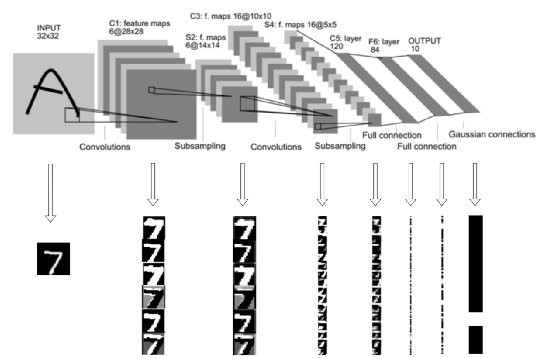
圖 8 LeNet5 Matlab實現中對應的每一層特征圖
三、基于LeNet5 CNN的FPGA硬件加速實現
表 2 LeNet5卷積神經網絡的架構和每層所需的內存大小
|
層 |
通道數 |
濾波器大小 |
步長 |
特征圖大小 |
內存大小 |
|
輸入層 |
1 |
32×32×1 |
1024×8 |
||
|
卷積層1 |
6 |
5×5 |
1 |
28×28×6 |
1024×6×16 |
|
池化層1 |
2×2 |
2 |
14×14×6 |
256×6×16 |
|
|
卷積層2 |
16 |
5×5 |
1 |
10×10×16 |
128×6×16 |
|
池化層2 |
2×2 |
2 |
5×5×16 |
32×16×16 |
|
|
卷積層3 |
120 |
5×5 |
1 |
1×1×120 |
128×16 |
|
全連接層1 |
84 |
1×1 |
1×1×84 |
||
|
全連接層2 |
10 |
1×1 |
1×1×10 |
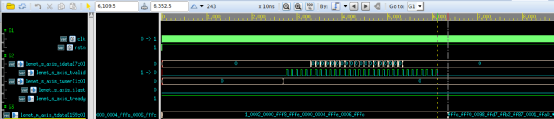
圖 13 延時優先的LeNet5卷積神經網絡的仿真結果
四、基于攝像頭的字符識別FPGA Demo的搭建與實現
效果如下,具體的內容,麻煩等書出版吧,謝謝
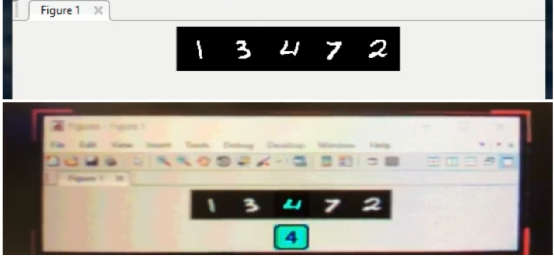
圖 16 字符識別的FPGA Demo系統實時識別,手寫字符由Matlab生成顯示在屏幕上,下面為FPGA Demo的實時識別結果。
原文標題:基于LeNet5的深度學習FPGA加速實現
文章出處:【微信公眾號:FPGA技術江湖】歡迎添加關注!文章轉載請注明出處。
-
FPGA
+關注
關注
1646文章
22092瀏覽量
620482 -
matlab
+關注
關注
189文章
3004瀏覽量
234906 -
卷積神經網絡
+關注
關注
4文章
369瀏覽量
12372
原文標題:基于LeNet5的深度學習FPGA加速實現
文章出處:【微信號:HXSLH1010101010,微信公眾號:FPGA技術江湖】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
FPGA實現LeNet-5卷積神經網絡
卷積神經網絡如何使用
卷積神經網絡模型發展及應用
基于矢量特征編碼的手寫字符識別技術
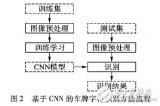
基于卷積神經網絡CNN的車牌字符識別方法
一種改進的仿射傳播聚類的手寫字符識別



















評論