引言

架構師的日常工作中，產生好的想法要占到我絕大多數精力。在兩年前，我寫過一篇《芯片架構方法學》的短文，目的是探索總結在芯片架構設計過程中，是不是有一些范式可以遵循，以提高過程中遇到的問題的解決速度。說白一點，就是能不能找到“靈感”發生的方法，進而用這個方法去生產方法。轉眼兩年又過去了，期間也一直在思考這個問題，偶有所得，跟大家聊聊。為了便于區別閱讀，文中加粗字體的是2.0主要增改的內容。

第一篇:回到定義

讓我們先從一個小游戲開始，

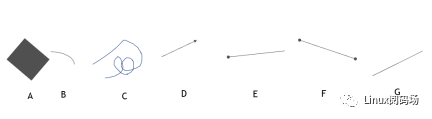
仔細觀察上面的幾個圖形，其中哪些是直線呢？可能很多人會毫不猶豫的回答是”G”。其實，要回答這個問題，我們就要先弄清楚“直線”的定義，直線必須滿足三個條件，第一，是直的；第二，是線，也就是必須是一維的，第三，直線沒有端點。那么上面有哪個是同時滿足這三個條件的圖形呢？沒有！A不是一維的，B/C不是直的，D/E/F有端點，G不是一維的，因為一維的直線是沒有寬度的，而G之所以能夠被我們人眼看到，說明它是有寬度的。

這里說這個小游戲的目的是為了引入一種非常重要的思維方式：回到定義。在我看來，我們平時遇到的很多問題，大部分可以通過“回到定義”來獲得一個快速的模糊的答案。為了說明這種思維方式的強大之處，我們來看幾個問題。

“這件衣服漂亮嗎？”

“我做的飯好吃嗎？”

“你覺得這個人勇敢嗎？”

“你覺得這個事情好不好做？”

“這個解決方案的成本高不高？”

“這個方案和那個方案，哪個好？”

“從這里去公司，開車快還是做地鐵快？”

“……”

無論是生活還是工作當中，我們無時無刻都會面臨上面類似的問題，這些問題可能來自家人，可能來自同事，也可能來自路人。要回答這些問題，同樣，也可以使用“回到定義”的思維方式，當我們弄明白定義之后，以上問題就迎刃而解了。

“什么是漂亮？”

“什么是好吃？”

“怎么定義勇敢？”

“怎么定義好做？”

“成本怎么定義？”

“怎么定義方案的好壞？”

“怎么定義快？”

你會發現，如果我們搞清楚了這幾個定義，其實那些問題也就自有答案了。

我們平時的工作，其本質是選擇，即，每時每刻要做出有利的選擇。針對芯片行業來說，可具體化為我們要選擇性能高（P），功耗低(P)，面積小(A)，復雜度低(C)的方案。一般情況下，大家在這個目標上是沒有分歧的，分歧的產生在于每個人對PPAC的預估值不同，或者在于每個人所站的角度不同。然而，一個方案的好壞不止PPAC這四個指標，還有很多其它的參數，有時候也需要考慮進去。還有，上面的提到的“有利的選擇”，對不同的人的含義也可能是不同的。最后，以上討論大多都是基于人是理性的這個假設，然而事實并非如此，這就使事情變得越來越復雜，難以有顯而易見的結論。

大道至簡，面對這紛繁復雜的多彩世界，我認為“回到定義”是我們可以利用的一把利器，“回到定義”一般不是為了解決某個問題，而是過濾那些價值不大的問題。

關于“回到定義”，從另外一個角度看，可以理解為“第一性原理”，比如，我們要解決某個問題，這個問題的答案往往就藏在問題本身。比如，芯片架構設計中經常面臨的問題：“如何提高芯片的powerefficiency”，解決這個問題，我們就可以嘗試以“回到定義”的方式來探索。

首先，我們可以提問：power是什么？或者說power都有哪幾部分組成？這個問題不難。Power一般可分為staticpower和dynamicpower。繼續“回到定義”，staticpower主要是leakagepower，繼續“回到定義”，根據MOS結構，leakagepower包含Drain->Well, Gate->Well，Source->Drain三部分。從前端設計的角度來看，這三部分主要受cell數量影響較大，所以，我們就可以嘗試減少area來減少power。然后，我們根據“排列組合”思路，繼續看dynamicpower，再次“回到定義”，dynamicpower=α·C · f · V^2

按照“排列組合”的思路，我們可以嘗試降低α、C、f、V。這里我們著重看一下f和V。直接降低freq，一般perf會成比例的降低，但有的時候不一定，比如，freq的降低，意味著clockperiod的增加，即，時序約束的放松，而時序約束的放松，一般會伴隨著area的降低，當area降低的程度超過perf降低的程度時（類比香農第三定理），就可以采用降低freq的方式提高powerefficiency。此外，我們可以將“freq”的本意做一些引申，比如freq可以認為是datareuse frequency,這樣一想，我們就可以嘗試從算法，memoryhierarchy等角度，提高datareuse rate,以降低“freq”，進而達到降低power的目的。我們再繼續看“Voltage”，可以通過采用更先進的process來降低Voltage，進而降低power。關于Voltage，這里有個細節，實際上，dynamicswitchpower的產生，主要是因為表示“0、1”邏輯的電壓差導致的，所以，從這個意義上講，借用物理學名詞，我們真正想降低的不是“絕對速度”，而是“相對速度”。

我們繼續“回到定義”，dynamicpower一般包含clocktree、missionfunction。所以做clockgating和datagating是降低power的非常重要的方法。當然，這里我們可以考慮“第一性原理”，能不能直接把clocktree去掉呢？因為clocktree去掉之后，自然也就不存在clocktree power了。答案是可以，即異步電路。

我們繼續“回到定義”，missionfunction上的power難道就是我們必須要買單的power嗎？不是，因為glitchpower就不是我們愿意付出的power代價。所以，我們可以嘗試降低glitch來降低power消耗，比如采用gray-code，調整clockskew。

我們已經“回到定義”很多次了，還可以繼續“回到定義”。。。

上面我們通過一個小例子，展示了“回到定義”這種思路的能力。我想表達的是，在具體的芯片設計過程中，遇到問題時，如果一時難以解決，可以嘗試“回到定義”，從問題本身尋找答案。

第二篇:排列組合

排列組合的本質是降維。

面對一個復雜的問題，當這個問題的復雜性已經超出我們解決問題的能力時，就會變得很棘手。一般情況下，出現這種情況是因為這個問題的維度超過了我們認知的維度，這時，我們可以采用“排列組合”的思維方式來嘗試解決。

比如“如何設計一個AI加速器”，這是一個很大的問題，我們可能很難在短時間內得到答案，因為這個問題的復雜性已經超出了很多人的認知范圍。這時，我們可以將這個問題進行降維處理，變成多個較簡單的，維度低一些的子問題：

“如何設計AI加速器的memoryhierarchy？”

“如何設計AI加速器的datapath？”

“如何設計AI加速器的controlpath？”

“如何設計AI加速器的運算單元？”

“如何使以上幾個子系統協同工作？”

我們仔細觀察發現，以上幾個問題是最開始問題的子問題，以及這些子問題之間的關系的問題。也就是原始的問題被降低到了更低的維度。如果發現個別子問題仍然不能解決，那么，可以采用同樣的方式，將這個子問題采用“排列組合”進行拆解。這里，我們假設“如何設計AI加速器的運算單元”這個子問題還是太復雜，超出了我們的能力，那么，我們可以進一步將其降維：

“如何設計AI加速器的Tensorprocessor？”

“如何設計AI加速器的Vectorprocessor？”

“如何設計AI加速器的Scalerprocessor？”

同樣，我們也可以繼續拆解：“如何設計AI加速器的Tensorprocessor？”

“AI加速器的Tensorprocessor負責完成哪些功能？”

“AI加速器的Tensorprocessor的sequence如何選擇？”

“AI加速器的TensorprocessorPPAbudget是怎樣的？”

“AI加速器的Tensorprocessor帶寬需求是怎樣的？”

“AI加速器的Tensorprocessor需要的dataformat是怎樣的？”

“……”

每個人解決問題的能力不同，所需要拆解到的問題的維度也不同，能力強的人，需要拆解的層數少一些，能力弱一些的人，可能需要將問題拆解到較低的維度時才能解決。

排列組合，除了可以將問題降維之外，還可以彌補腦容量不足所帶來的問題。平時工作當中，有一類問題難度太高，一時無法下手，可以采用排列組合來解決，正如上面剛剛提到的例子；還有另外一類問題，其本身難度并不高，在我們解決問題能力范圍之內，但問題比較繁雜，怎奈腦容量有限，一時難以將所有情況都考慮周全。對于這樣的問題，也可以采用“排列組合”來防止遺漏。這個時候，“好記性不如爛筆頭”就會發揮作用，當我們列出所有排列組合之后，然后用大腦依次分析，就能得出結論了。

上面最開始提到“排列組合的本質是降維”，降維，即，將問題拆解，是解決問題重要的手段。從相反的方向看，“排列組合的本質也可以是升維”。我發現“升維”竟然也可能利于問題的解決。比如，我們在武俠電影里經常看到以下場景。兩個武俠高手最開始在地上打幾個回合，幾個回合過后，如果勝負未分，就會跳到房頂上，或者飛在空中，繼續打。此外，我們也知道，在戰爭中，制空權一旦喪失，地面部隊會變得非常被動。還有，在芯片封裝時，如果芯片面積太大，可以做多層mask，甚至用3Dstacking。我們發現，“飛到空中”、“制空權”、“3Dstacking”的共同點是提高了問題解決的維度。在芯片架構時，這種思路有的時候也非常有用。比如，我們遇到一個問題，這個問題長時間都沒有解決，采用“排列組合”的降維方式，發現tradeoff的點非常難受，顧此失彼，按下葫蘆浮起瓢。如果面臨這種情況，很可能是在目前的維度上，已經不存在明顯的矛盾，真正的矛盾已經轉移到了更高的維度上。這個時候，我們可以嘗試“升維”，比如前面提到的clocktreepower優化問題，如果我們已經采用了很多方法來降低clocktree power，但是距離目標還是很遠，這個時候，去掉clock就是一種升維，跳出原來優化clocktree power的維度，“飛到空中”。從這個角度看，當“山重水復疑無路”時，采用“升維”，說不定可以“柳暗花明又一村”。

這里需要澄清的是，“升維”不一定是維度的增加，也可以是維度的轉換。比如，問題如果在空間上難以解決，就可以考慮將問題在時間上解決，反之亦然。比如，我們可以通過增加area來解決timing問題，也可以通過增加timing來解決area問題，可以通過增加area來降低power，也可以犧牲power來節省area，總之，PPAC四個維度都可以相互轉換，就好像,area和M對應，timing和C對應，而power，很顯然可以和E對應。

第三篇論數據

當今時代是一個信息爆炸的時代，天量的數據無時無刻的被生產，收集，傳播開來，數據分析與篩選技能已經是一個人最基本的技能之一了，經過常年的學習與訓練，關于數據的能力很多都已經變成了我們的前意識記憶，甚至是在非意識范圍內影響著我們。這一點對于IT從業者尤其明顯，在平時的工作中，無論是誰，每天都會面臨很多“選擇題”，而我們要做出選擇，大多是出于理性的，而理性本身需要數據支撐。

“為什么采用這個方案，有什么好處嗎？”

“這個方案的PPAC怎么樣？”

“如果采用這個方案，會有什么代價？”

“……”

在做出以上選擇之前，大多需要準備一些數據，而一個沒有任何數據支撐的問題的決定能力是一個人重要的技能，對兩個或者多個方案，數據上難分伯仲時的決策能力也是一個人重要的技能。

另外，數據有結論之前的數據和結論之后的數據之分。前者使我們自信，后者使我們開心。全面的數據使我們柳暗花明又一村，走出泥潭，片面的數據使我們不識廬山真面目，誤入歧途。“實事求是，不先入為主”是SOL,“求全責備，所有決定都要有數據支撐”也是SOL，需要知道的是SOL我們人類做不到的。

給紛繁的世界建模以獲取數據是困難的，在天量的數據中做出正確的決定也是不易的。數據不會騙人，騙人的是使用數據的人而已。我建議的是，工作中80%的決定要基于收集到的數據，20%的決定要基于內心。生活中20%的決定要基于收集到的數據，80%的決定要基于內心。類似模擬退火。理性是可貴的，但感性也不是一文不值。智慧是好的，但我們也不能倚靠自己的聰明。追求完美，大多數情況是褒義詞，但有時候也可以是貶義詞。

第四篇正反合（A=A=!A）

A=A=!A這個式子可以先拆成兩個簡單一點的式子來看：

A=A 和A=!A，為了便于描述，我稱第一個式子為“A向左運動”，第二個叫“A向右運動”。

無論是在工作還是在生活中，我們的核心工作就是解決這樣或那樣的問題。以上提到的幾種方法之所以有用，很大程度上是因為我們發現了問題的矛盾點。如果把“A向左運動”看成是“證明方案A是對的（矛）”的話，那么“A向右運動”就是“證明方案A是錯的（盾）”。矛與盾相互否定，推動盾與矛互相肯定，這個過程反復出現，實現了問題的瓦解，即，問題的解決，達到了新的穩態，新的合理，新的存在。

比如，我們要新加一個具體的feature，最開始，我們會提出一個方案，假設就叫方案A，方案A的提出過程，其實就是“A向左運動”，這個過程中，最重要的是要確定“方案A確實可以解決這個問題”，就是A的肯定。一旦方案A提出之后，隨之而來的是“為什么方案A有這個缺點”或者“為什么不選擇方案B”，這個過程就是“A向右運動”的過程，即方案A的否定。接下來，就又是“A的肯定”過程，即，要完善最開始的方案A，完善之后可能還有反對者提出問題，如此往復，經過幾個回合的拉鋸之后，方案A漸趨成熟，而這時方案A還是方案A，方案A也是方案A的否定了。“追求無我，成就自我”，“無知者是不自由的”，每一次的否定自我，就是一次自我的肯定，每一次的自我肯定，都是向對立陌生的一次前進。

A=A=!A就是“正”，“反”，過程是螺旋上升的，目的是“合”。然而，世界是復雜的，我們偶爾也會遇到一時沒有矛盾，但仍然需要我們解決的問題，這個時候，用我們人類最柔軟的內心與這個問題握手。

第五篇虛與實

相對于上一版，本篇的虛與實是新加的內容。

經過觀察，我發現很多工程師，包括我自己在內，有的時候，在遇到問題后，最開始，第一步，就是嘗試各種方法，我稱之為“試錯調試法”，期望通過多次的嘗試，只要syndromeisgone，就算問題解決了。在解決比較簡單的問題時，這種方法或許會奏效，但如果要解決比較困難的問題，“試錯調試法”的效率就可能變得很低，這個時候我們該怎么辦呢？我感覺，可以分成以下幾個階段：

Problem->modeling->SOL(First-principles)->reference->actual/solution->correction

首先，我們要認清問題，即，我們要先定義問題(problem definition)，所謂“知己知彼”中的“知彼”。

在認清問題后，我們要對這個問題建模(modeling)，最好用抽象的數學模型。

確定好數學模型之后，我們就可以求解這個模型，得到理想解，這里稱為SOL（speedof light），這個理想解是盡量不考慮邊界條件下的解。最好從前面我們提到的“第一性原理”出發。這個理想解非常重要，類似于我們的“希望”，設想，在沒有希望的情況下工作，會是多么的不安。

理想是美好的，現實可能是殘酷的。在擁有理想解之后，下一步，我們要低頭看看，面對現實。這個階段，可以查一些資料，看看已有的解決方案，分析自己的實際，即，邊界條件，或約束條件。

理想與現實都有之后，我們就可以坐下來，考慮制定從現實到理想的行進路徑，提出當前狀況下的解決方案（solution）。

最開始的solution不用完美，根據前面提到的“正反合”思路，不斷迭代，優化，即自我修正（correction），在修正的時候，就會再次發現新的problem。對于新的problem，從第一步開始。

這樣就形成了問題解決的閉環。仔細觀察，上面幾個階段是虛實交替的。類似于真空的磁場與電場，相互激發，共同傳播，與光同行。

這里想著重提一下“SOL”,先抬頭看天，再低頭看路，要過有“希望”的日子。比如，我們IT領域，處理的是各種各樣的數據，其中，數據的壓縮，是非常常見的，普遍使用的技術，那么，給定一段數據，假設壓縮方法不限（無損壓縮），那么有沒有一個理論上的最小值？如果有，我們壓縮之后的最小數據量是多少呢？其實，答案是Yes，這個最小值可以通過香農定理給出：

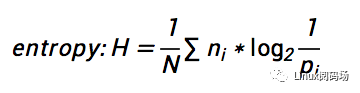
一旦知道了這個理論下限，我們就有了希望，有了開始的希望，也有了結束的希望。

有意思的是，這個定理可以給我們很多啟示。比如，我們經常說的“信息”是什么？從定理中可以看出，“信息”可以理解為“概率”，并且概率越小，信息量越大。即，一成不變的東西，本身沒有任何信息，因為其，簡單計算可知H=0。進而說明，“千篇一律”，“人云亦云”等，并不會增加這個世界的熵，世界需要“鶴立雞群” 、“一鳴驚人”。

番外篇關于芯片架構

以上討論了幾種個人解決實際問題的方式方法，接下來說一下對芯片架構工作的體會。

芯片架構，大體上可分為三個事情：Architecture, Algorithm和Association。顯然，架構工作，是要生產一些架構（Architecture）作為產品的，作為設計人員的參考與指導。架構本身并不是無根之木，是需要一些數據支撐的，而這數據的來源，主要是算法分析，所以架構工作還應包括一些算法分析的內容，此外，為了發揮所做架構的效力，應該提供一些基本的工具來幫助用戶。三者之間，相輔相成，不同階段，不同情況，重要程度不同。算法分析者可以提供必要的信息，比如算法發展趨勢，所關心領域算法特點等重要內容，架構者基于這些內容，可以提出合適的硬件架構來，而另外一些人可以提供合適的工具來彌補架構和客戶之間的gap。三者之間不是單向影響的，是互相關聯的，架構者可以提出在做架構時的痛點，以影響算法發展和工具提供者。

芯片架構工作，很像是玩打地鼠游戲，目的不是把從某個洞里出來的地鼠全部打死，而是能夠權衡，使總體得分最高，而權衡中的原則是，如果自己與非自己有沖突時，或者正義與利益有沖突時，盡量使非自己開心。

開始工作的前幾年，要先建立自己的知識體系，而后，要慢慢建立自己的哲學體系。

審核編輯 ：李倩