凝聚態(tài)物理中,有一些最基本的參量,其效用是普適的,并規(guī)范著一些最基本的物理性質(zhì)。相信讀者均認(rèn)可,體系的時空維度,即為此中一元 (本文只限于空間維度)。
凝聚態(tài)系統(tǒng)中,維度是理解其物理的基本要素,從而被給予格外關(guān)注。物理人都將納米科學(xué)的起源,與費曼于 1959 年在 APS 會議上所作的《底層的豐富》演說聯(lián)系起來。我們猜,那時候費曼的心目中,“底層”應(yīng)該就是低維,而不會只是指普通意義上的納米顆粒或準(zhǔn)零維體系。現(xiàn)在,我們早就耳熟能詳凝聚態(tài)系統(tǒng)中維度的作用。
Ising 非此道中人,主要從書本中零存整取對維度的感受,如圖 1 所示。對材料科學(xué),也能隨手舉幾個曾經(jīng)聽說過、或膚淺參與過的具體例子,與維度有一些內(nèi)在的聯(lián)系 (不追求準(zhǔn)確,但追求“醒目”):
(1) 晶粒長大:材料中晶粒長大或疇長大是普遍現(xiàn)象,但其物理未必簡單。以各向同性體系中晶界能驅(qū)動的晶粒長大為例,其長大動力學(xué)就與維度密切相關(guān)。材料教科書很早就寫明,1960 年代,Lifshitz、Slyozov 和 Wagner 三位學(xué)者在前人研究基礎(chǔ)上,提出了那著名的、以其名字命名的晶粒長大 LSW 動力學(xué)理論:在等溫條件下的晶粒長大后期,晶粒平均尺寸 R 與時間 t 之間滿足 1/d 冪指數(shù)定律,這里 d 乃空間維度。也就是說,塊體材料晶粒長大滿足 1/3 冪律,準(zhǔn)二維薄膜晶粒長大滿足 1/2 冪律,雖然真正的一維線晶粒長大動力學(xué)還是一個問題。
因為實驗體系摻雜了各種因素,這一規(guī)律的驗證曾經(jīng)很有曲折,引發(fā)過 1990 年代歐美物理學(xué)家和材料學(xué)家對此冪律的質(zhì)疑。質(zhì)疑之火前后延續(xù)十多年,最后還是被大規(guī)模計算模擬和精細(xì)實驗驗證所澆滅:1/d 冪律才是正確的。小編以為這是材料科學(xué)史上維度勝出的一段佳話。
(2) 磁性:磁學(xué)中維度的意義更被彰顯,并屢屢影響其發(fā)展進(jìn)程。雖然磁學(xué)更多具有量子本質(zhì),但不妨礙對經(jīng)典磁學(xué)的維度討論。從 Ising 模型開始,一維模型不存在有限溫度的相變,到二維模型那著名的嚴(yán)格解,再到三維模型嚴(yán)格解依然是世紀(jì)難題,都是磁學(xué)和統(tǒng)計物理學(xué)知名的歷史故事。然而,實際晶體中,給一維和二維磁體定義 Ising 自旋,未必合理,因為那各向異性無窮大的兩重態(tài)缺乏微觀物理來源:一個單層的磁性原子層,靠什么能夠約束其自旋只能上下兩重態(tài)?自旋軌道耦合好像不夠。因此,嚴(yán)格滿足二維 Ising 模型的體系不大可能存在。
另外一個極端,就是各向同性的海森堡二維自旋體系,成就了那個著名的 Mermin – Wagner (MW) 定理:各向同性的海森堡磁性二維體系沒有長程序。這一定理讓多少物理人意興闌珊、收兵回朝,不再深入探討二維磁性問題,直到近來被接近真實的二維磁體具有長程序的實驗所驚詫。今天的二維磁性正方興未艾,當(dāng)然并非 MW 定理的錯,而是因為真實的二維磁體未必就是單純一層磁性原子排列而成。那些二維材料,其晶格單元依然存在面外結(jié)構(gòu),第三維特征依然存在,依然可以施加磁晶各向異性。再加上目前的實驗樣品在 xy 平面的尺度有限,邊緣效應(yīng)也可能導(dǎo)致磁性異常。Ising 不懂二維磁性,只是借助道聽途說而了解了一些磁性維度效應(yīng)的復(fù)雜性。
(3) 鐵電:鐵電物理中維度效應(yīng)也很重要,導(dǎo)致鐵電體維度的研究比磁性材料人去關(guān)注維度的歷史還要久遠(yuǎn)。從退極化這一簡單圖像去預(yù)言鐵電尺寸效應(yīng),言之灼灼、語之戳戳,都是 1990 年代之前的事情了。一些成果還被明明白白寫在諸如鐘維烈老師的《鐵電物理學(xué)》著作中。鐵電體的維度效應(yīng),一直是鐵電物理的前沿,也與現(xiàn)代集成鐵電技術(shù)發(fā)展密切相關(guān)。不過,過去幾十年,鐵電物理人將這個尺寸和維度極限不斷地推向底層,包括納米線、單個晶胞厚度的薄膜、撕扯出來的 vdW 二維材料。也不知道是該高興還是該失望,這個鐵電尺寸效應(yīng)并不明顯,更不要說預(yù)言的鐵電維度極限正在不斷被壓縮。這些結(jié)果,將經(jīng)典教科書中鐵電尺寸效應(yīng)的那幾頁物理戳得千瘡百孔,也可見鐵電維度效應(yīng)的復(fù)雜性。
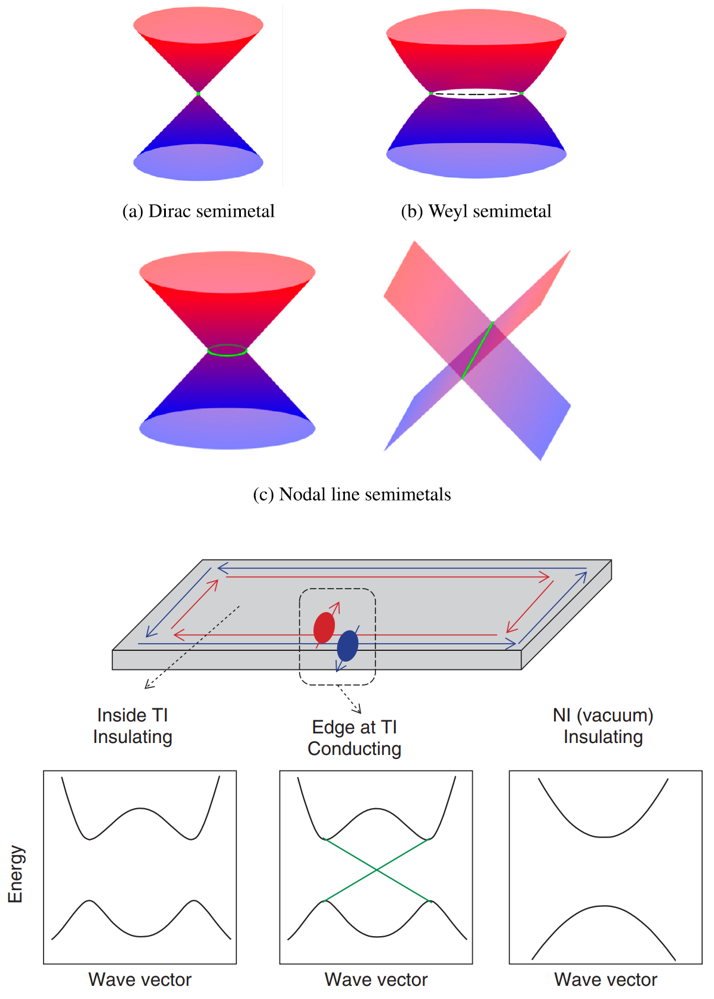
圖 2. 拓?fù)淞孔硬牧现芯S度的對應(yīng)關(guān)系 (無需詳細(xì)解讀)。
上圖來自:S. Y. Yang et al, Symmetrydemanded topological nodal line materials, Adv. Phys. X3, 1414631 (2018), https://doi.org/10.1080/23746149.2017.1414631
下圖來自:https://www.ntt-review.jp/archive/ntttechnical.php?contents=ntr201707fa6.html
這些具有歷史韻味的實例告訴我們,維度可以影響介觀微結(jié)構(gòu)、影響對稱性、影響相變,OK,及至影響一切。但這些例子也告訴我們一些簡單的事實:理論預(yù)言的、理想化約束條件下的維度物理,在實際材料中未必滿足。個中差池,就給了低維物理突出重圍、產(chǎn)生新效應(yīng)和新應(yīng)用的機會,體現(xiàn)了現(xiàn)實總是在理想化的極端之間取道“中庸”的事實。也許物理本來就是如此,只是需要我們?nèi)ァ爸淙徊⒅渌匀弧保源税l(fā)現(xiàn)和利用之、并企圖造福人類。
這種認(rèn)識的后果,就是今天物理人對低維凝聚態(tài)和低維量子材料的廣泛研究,包括那些熱點實例,如碳 60、碳納米管、石墨烯,如 vdW 二維材料、魔角二維材料,如界面二維電子氣、量子阱等。其中,對當(dāng)下的拓?fù)淞孔硬牧希S度顯得更為別致和新奇,如圖 2 所示。不知道小編 的如下理解是不是算胡謅:
(1) 非磁性拓?fù)浣^緣體,因為費米面附近的拓?fù)浞瞧接鼓軒ЫY(jié)構(gòu),存在體 - 面對應(yīng)性,即三維絕緣體態(tài)對應(yīng)二維表面金屬態(tài)。
(2) 磁性拓?fù)浣^緣體,因為費米面附近的拓?fù)浞瞧接鼓軒ЫY(jié)構(gòu)和磁性,存在體 - 邊對應(yīng)性,即三維絕緣體對應(yīng)二維表面能隙和一維自旋極化的邊緣金屬態(tài)。
(3) Weyl 半金屬,也因為費米面附近的拓?fù)浞瞧接鼓軒ЫY(jié)構(gòu),存在三維半金屬態(tài)、二維表面費米弧和零維的“磁單極點”。
所以,我們看到了,拓?fù)淞孔硬牧现心切┚S度的表象顯得更加突出,因為動不動就是整數(shù)維度的量子材料新效應(yīng),如三維絕緣體、二維金屬、二維費米弧、一維金屬、零維 Weyl 點 (磁單極子)。好吧,物理人說還遠(yuǎn)不止于此,當(dāng)下那些 cutting – edge 問題包括費米面附近出現(xiàn)的那些零維的節(jié)點 (nodal point)、一維的節(jié)線 (nodal line)、二維的節(jié)面 (nodalsurface)。
維度,在這里就是一張無形而有實的大手,“掌控”著量子材料、拓?fù)淞孔硬牧稀?/p>
有意思的是,這些拓?fù)淞孔硬牧系牡途S性質(zhì),似乎絕大多數(shù)附屬于三維體態(tài)。諸如碳納米管和石墨烯這樣“真正的”、“獨立自主的”一維和二維拓?fù)淞孔硬牧喜⒉欢嘁姡辽偃缡┻@般知名的低維拓?fù)洳牧喜欢唷2贿^,過去一些年,二維材料不斷發(fā)展,二維量子材料家族也很興旺。如此,必然催動物理人走向更底層:那,有沒有真實的、獨立自主的一維量子材料?甚至是一維拓?fù)淞孔硬牧希?/p>
挺好的問題!要說凝聚態(tài)物理和量子材料中有什么重要的問題無人問津,那倒極為困難。通過各種微納制備技術(shù),已經(jīng)獲得的一維、準(zhǔn)一維量子材料很多,研究歷史也不短。例如,在固體表面生長一些納米線總是可以的,或者通過其它技術(shù)手段“制造”出一維、準(zhǔn)一維結(jié)構(gòu),也不是難題。過去這些年,利用有機材料獨特的分子結(jié)構(gòu)設(shè)計和合成技術(shù),制備一維有機量子材料的機會要大一些,包括電荷密度波、Peierls 相變、孤波、自旋 - 電荷分離以及那個著名的 Su – Schrieffer – Heeger(SSH) 理論預(yù)言的能帶拓?fù)鋺B(tài)等,也多有見諸報道。
但是,到目前為止,一維無機多元復(fù)雜化合物量子材料,包括一維無機拓?fù)洳牧系摹爸圃臁保蟾挪蝗菀住H粢f容易,那必然是新穎別致和值得推崇的!
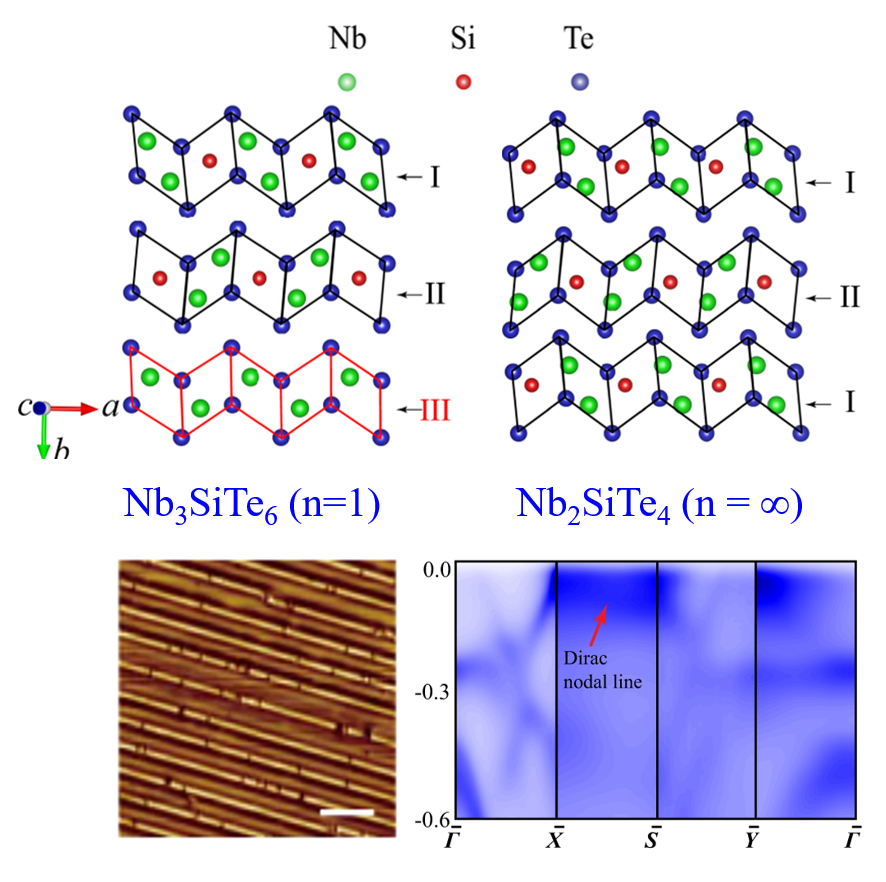
圖 3. 柳仲楷和陳宇林老師他們關(guān)注的體系:NbSixTe2(x?=?0.33 to 0.5) 或Nb2n+1SinTe4n+2 (n?=?1,2,…, ∞):結(jié)構(gòu)、樣品表面一維鏈的實物形貌及能帶中清晰的Dirac nodal line。
最近,上海科技大學(xué)的柳仲楷和陳宇林老師他們,聯(lián)合南京大學(xué)、新加坡科技設(shè)計大學(xué)、勞倫斯伯克利實驗室和清華大學(xué)的同行們合作,就在一維拓?fù)淞孔硬牧蠁栴}上邁出了一“小”步。這里的“小”,是走向底層的“小”。他們將一些結(jié)果整理后,發(fā)表在《npj QM》上,讓小編有機會學(xué)習(xí)和領(lǐng)會他們的工作,并寫幾句粗淺的學(xué)習(xí)心得。
陳宇林和柳仲楷老師他們都是 ARPES 的行家,一定是做夢都想利用這一有力工具去探測那些一維量子材料能帶結(jié)構(gòu)和拓?fù)淞孔有滦?yīng)。不過,ARPES 的探測技術(shù)原理注定了樣品不能是一根孤零零的一維鏈,必須是足夠多的、且有序地排列的一維鏈集合體!這種情形很像中子散射實驗。針對單一的二維或一維材料的中子散射,到今天依然是巨大挑戰(zhàn):樣品要有足夠的體量!
問題是,這樣的機會太小了。問題更是,這樣的機會他們有意地“碰”上了!
最近一些年,已經(jīng)有量子材料人關(guān)注那些組成可調(diào)控的無機化合物,如 NbSixTe2 (x?=?0.33 to 0.5) 或 Nb2n+1SinTe4n+2(n?=?1, 2,…, ∞),它們在結(jié)構(gòu)上天然就能形成有序排列的準(zhǔn)一維 NbTe2 鏈。通過調(diào)控組分 x或 n,這一有序排列的鏈狀結(jié)構(gòu)間距可以變化,從而有可能獲得從一維到二維連續(xù)可調(diào)的量子材料體系。
更因為,這種一維鏈狀結(jié)構(gòu)可以整齊劃一地定向有序排列,堆砌于整個三維晶體中,給 ARPES 探測這些一維鏈提供了現(xiàn)實的可行性。而且,如上所述,調(diào)節(jié)組分 x,讓這些一維鏈相互靠近,實現(xiàn)從一維走向二維、甚至三維鏈?zhǔn)倪^渡成為可能。
陳老師和柳老師他們團(tuán)隊,似乎就這樣“輕而易舉”地搞定了研究對象。接下來,這些一維鏈就是他們的“刀下魚肉”,聽?wèi){其“宰割”了。
這篇文章主要展示了如此精巧的準(zhǔn)一維結(jié)構(gòu) (metallic NbTe2 chains) 的電子結(jié)構(gòu)特征,特別是其非平庸拓?fù)涮匦浴5玫降闹饕Y(jié)論是:能帶費米面附近的狄拉克半金屬態(tài),乃是具有節(jié)線的狄拉克態(tài) (Dirac nodal line structure),受晶體與時間反演對稱保護(hù)。這樣一個節(jié)線狄拉克半金屬體系,通過適當(dāng)結(jié)構(gòu)調(diào)控和磁性摻雜,有可能得到 Weyl 半金屬及新穎的拓?fù)溥吘墤B(tài)。通過增加 NbTe2 一維鏈的密度 (減小其間距),ARPES 也清楚展示了能帶結(jié)構(gòu)及其拓?fù)涮卣鲝囊痪S向二維的轉(zhuǎn)變,如圖 4 所示。整個文章的故事新穎、物理圖像清晰明了。
拓?fù)淞孔游锢淼年P(guān)注點,主要是動量空間中能帶結(jié)構(gòu)的維度花樣。本文所展示的拓?fù)淞孔泳S度效應(yīng),關(guān)注點則正走向?qū)嵖臻g的維度花樣。這是量子材料人科研生命中必然的元素及張力,也給了凝聚態(tài)物理以更豐富的維度與形態(tài)。雖然這些花樣能不能最終走向為人所用尚未有答案,但可控制造實空間可組裝的不同維度體系、并賦予其拓?fù)淞孔庸δ埽且I(lǐng)性的一步。阿門!
當(dāng)然,柳、陳團(tuán)隊針對的一維 NbTe2 一維鏈,卻還是依附于 Nb2n+1SinTe4n+2 晶體內(nèi)部的,距離“真正的”、“獨立自主的”一維體系,還是差那么一點!
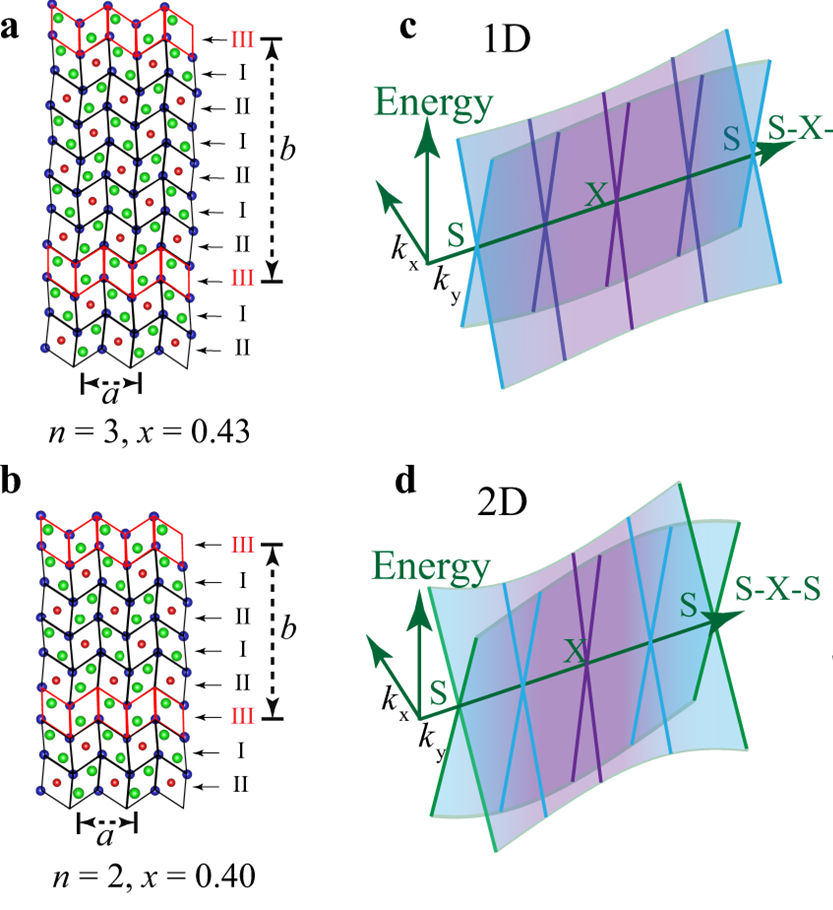
圖 4. 隨著 x 或者 n的變化,Nb2n+1SinTe4n+2體系從1D走向2D的過程,對應(yīng)的拓?fù)淞孔討B(tài)也發(fā)生演化。
審核編輯 :李倩
- 拓?fù)?/span>
- 磁性材料
-
晶粒
+關(guān)注
關(guān)注
0文章
29瀏覽量
3934
原文標(biāo)題:維度的拓?fù)?/p>
文章出處:【微信號:bdtdsj,微信公眾號:中科院半導(dǎo)體所】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
開關(guān)電源設(shè)計如何選擇合適拓?fù)?/b>
開關(guān)電源功率變換器拓?fù)?/b>與設(shè)計
開關(guān)電源拓?fù)?/b>結(jié)構(gòu)介紹
反向降壓拓?fù)?/b>如何替代非隔離反激式拓?fù)?/b> 德州儀器反向降壓拓?fù)?/b>詳細(xì)解析
常見的PFC拓?fù)?/b>架構(gòu)及控制方法
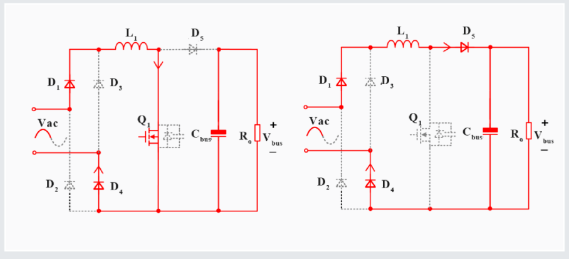
開關(guān)電源各種拓?fù)?/b>集
移相全橋ZVS及ZVZCS拓?fù)?/b>結(jié)構(gòu)分析
激光自身空間維度加工系統(tǒng)綜述

AI云端計算資源的多維度優(yōu)勢
DHB拓?fù)?/b>出現(xiàn)輸出電壓噪聲怎么解決
CAN總線十萬個為什么 | 聊聊幾種常見的CAN網(wǎng)絡(luò)拓?fù)?/b>

LDO芯片的拓?fù)?/b>結(jié)構(gòu)
在反相降壓/升壓拓?fù)?/b>中使用 TPS62120應(yīng)用說明







 維度的拓?fù)?/h1>
維度的拓?fù)?/h1>













評論