1 暴力破解法
在主串A中查找模式串B的出現位置,其中如果A的長度是n,B的長度是m,則n > m。當我們暴力匹配時,在主串A中匹配起始位置分別是 0、1、2….n-m 且長度為 m 的 n-m+1 個子串。
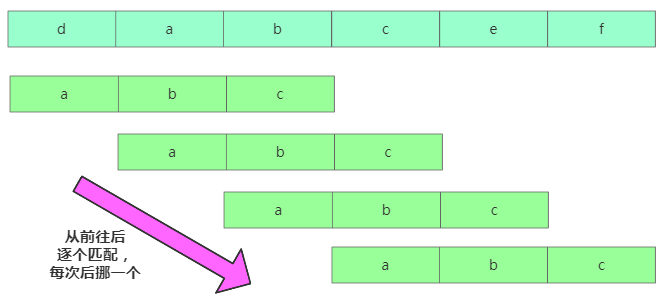 暴力匹配
暴力匹配對應代碼是:
#include
如果主串是bbb…bbb,模式串是bbbbc,那每個串都要比較m次,一共是(n-m+1)*m次。時間復雜度很大 = O(n*m),一般簡單匹配時候可用此法。
2 Rabin-Karp 算法
算法思路:對主串的 n-m+1 個子串分別求哈希值,然后跟模板串的哈希值對比,如果一樣再逐個對比字符串是否一樣。
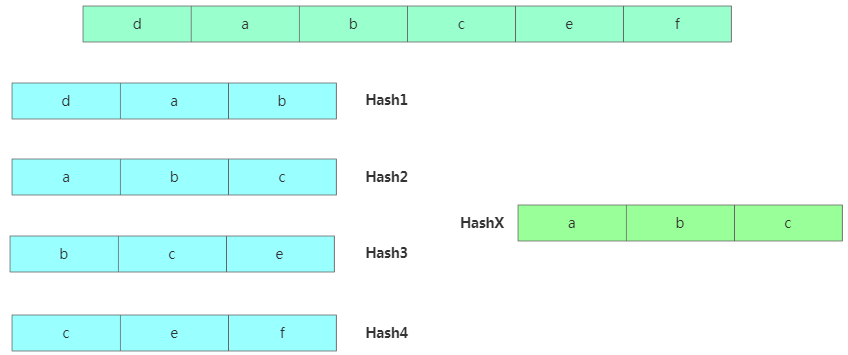 Rabin-Karp算法
Rabin-Karp算法但是中間數據的Hash值計算是可以優化的,我們以簡單的字符串匹配舉例,把a-z映射到0~25上。然后按照26進制計算一個串的哈希值,比如:
 Hash計算
Hash計算但是你會發現相鄰的兩個子串數據之間是有重疊的,比如
dab跟abc重疊了ab。這樣哈希下一個數據的Hash值其實可以借鑒下上一個數據的值推導得出: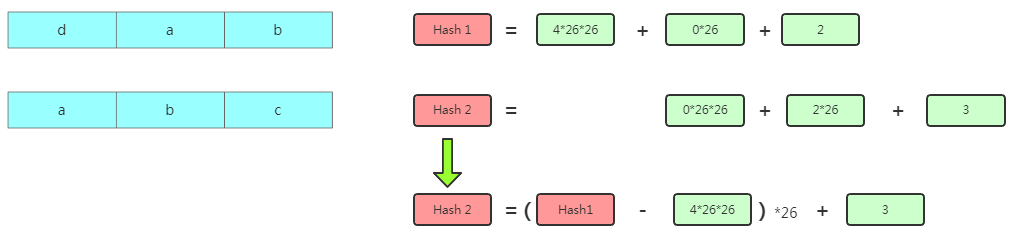 優化計算哈希值
優化計算哈希值RK算法的時間復雜度包含兩部分,第一部分是遍歷所有子串計算Hash值,時間復雜度是O(n)。第二部分是比較哈希值,這部分時間復雜度也是O(n)。
這個算法的核心就是盡量減少哈希值相等的情況下數據不一樣從而進行的比較,所以哈希算法要盡可能的好,如果你感覺用123對應字母abc容易碰撞,那用素數去匹配也是OK的,反正目的是一樣的, 你可以認為這是一種取巧的辦法來處理字符串匹配問題。
3 Boyer-Moore 算法。
Boyer Moore算法是一種非常高效的字符串匹配算法,它的性能是著名的 KMP 算法的 3 到 4 倍。它不太好理解,但確是工程中使用最多的字符串匹配算法。以前我們匹配字符串的時候是一個個從前往后挪動來逐次比較,BM 算法核心思想是在模式串中某個字符與主串不能匹配時,將模式串往后多滑動幾位,來減少不必要的字符比較。
 移動比較對比
移動比較對比整體而言BM算法還是挺復雜的相比前面兩種,主要包含
壞字符規則跟好后綴規則。
3.1 壞字符規則
壞字符規則意思是根據模式串從后往前匹配,當我們發現某個字符沒法匹配的時候。我們把這個沒有匹配的主串中的字符叫作壞字符。
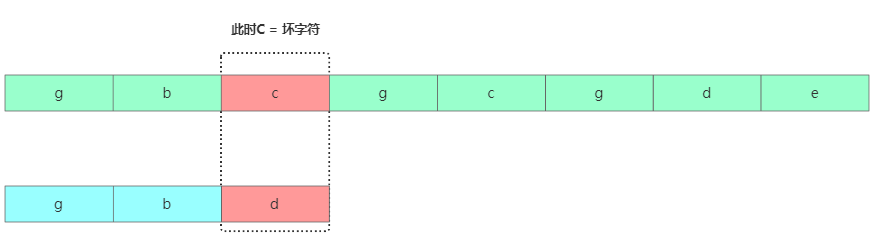 壞字符
壞字符找到壞字符c后,在模式串中繼續查找發現c跟模式串任何字符無法匹配,則可以直接將模式串往后移動3位。繼續從模式串尾部對比。
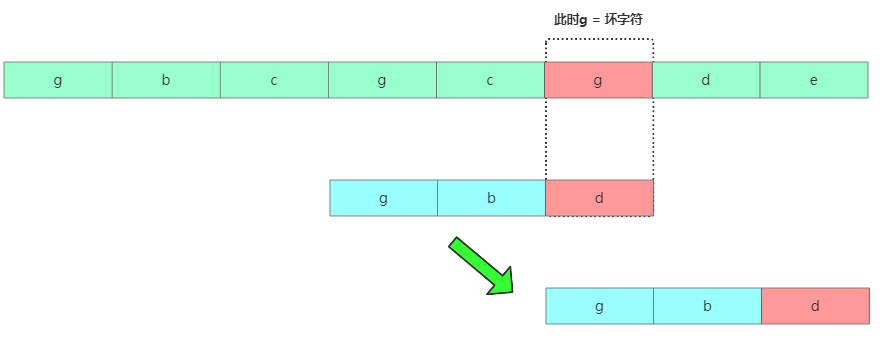 移動2格
移動2格此時發現壞字符是g,但在模式串中有個g存在,不能再往后移動3個了,移動的位置是2個。再繼續匹配。那有啥規律呢?
發送不匹配時,壞字符對應的模式串字符下標位置Si,如果壞字符在模式串中存在,取從后往前最先出現的壞字符下標記為Xi(取第一個是怕挪動太大咯),如果壞字符在模式串中不存在則Xi = -1。此時模式串往后移動位數= Si - Xi。
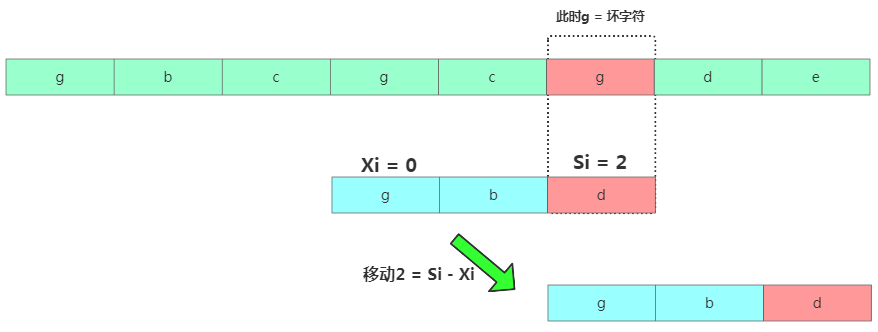 壞字符移動規則
壞字符移動規則如果碰到極致的主串=cccdcccdcccd,模式串=cccc,那此時時間復雜度是O(n/m)。
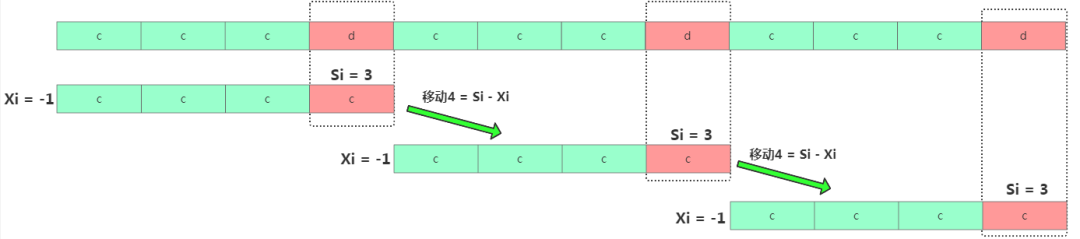 最優解
最優解但是不要高興太早!下面這種情況可能導致模式串不往后移動,反而往前移動哦!
 往前移動?
往前移動?所以此時BM算法還需要用到
好后綴規則。
3.2 壞字符代碼
為避免每次都拿懷字符從模式串中遍歷查找,此時用到散列表將模式串中每個字符及其下標存起來,方便迅速查找。
接下來說下散列表規則,比如一個字符是一個字節,用大小為256的數組記錄每個字符在模式串出現位置,數組中存儲的是模式串出現的位置,數組下表是字符對應的ASCII值。
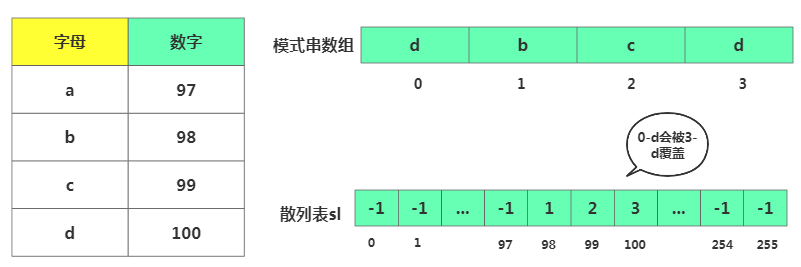 哈希規則
壞字符規則:
哈希規則
壞字符規則:
//全局變量 SIZE
privatestaticfinalintSIZE=256;
//b=模式串數組,m是模式串數組長度,sl是哈希表,默認-1
privatevoidgenerateBC(char[]b,intm,int[]sl){
for(inti=0;i-1;//初始化sl
}
for(inti=0;iintascii=(int)b[i];
sl[ascii]=i;
}
}
接下來先不考慮好后綴規則跟壞字符的負數情況,先大致寫出 BM 算法代碼。
 壞字符BM
壞字符BM
publicintbm(char[]a,intn,char[]b,intm){
//記錄模式串中每個字符最后出現的位置
int[]sl=newint[SIZE];
//構建壞字符哈希表
generateBC(b,m,sl);
//i表示主串與模式串對齊的第一個字符
inti=0;
while(i<=?n?-?m)?{
????intj;
for(j=m-1;j>=0;j--){
if(a[i+j]!=b[j])break;
}
if(j0){
//匹配成功,返回主串與模式串第一個匹配的字符的位置
returni;
}
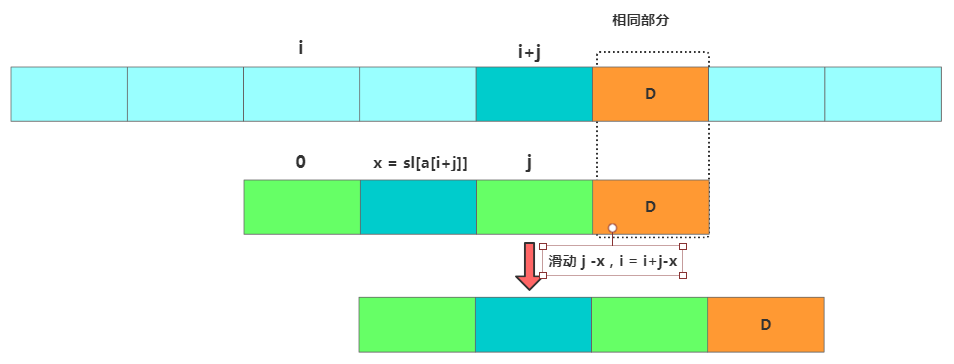
//將模式串往后滑動j-bc[(int)a[i+j]]位
i=i+(j-sl[(int)a[i+j]]);
}
return-1;
}
3.3 好后綴規則
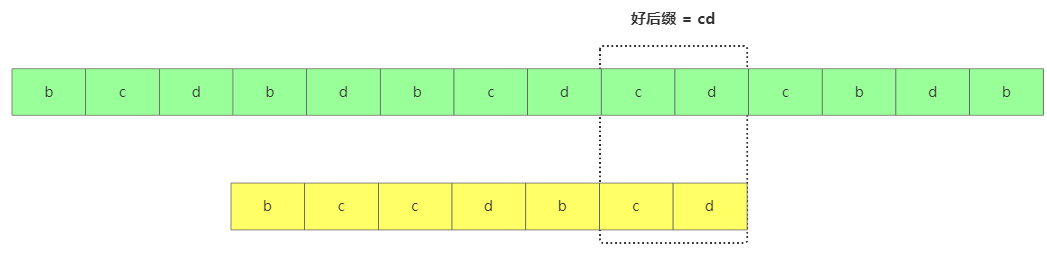
好后綴跟壞后綴道理類似,從后往前匹配,直到遇到不匹配的字符x,那主串x之前的就叫好后綴。
 好后綴定義
好后綴定義此時移動的規則如下:
-
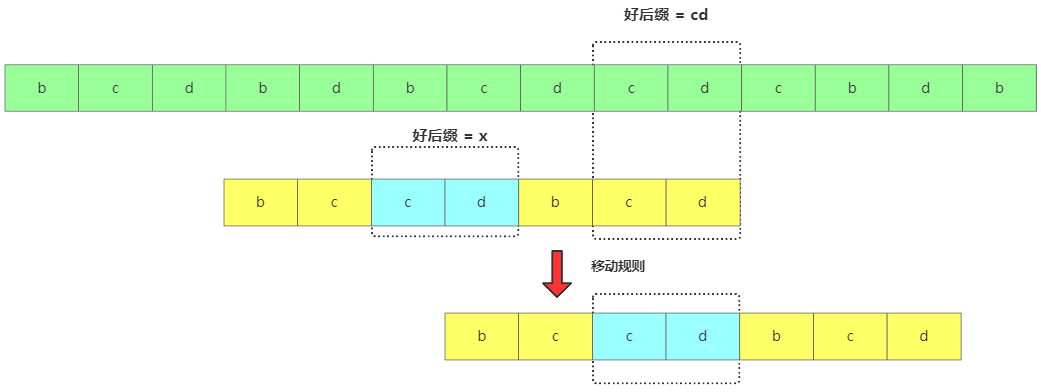
如果好后綴在模式串中找到了,用x框起來,然后將x框跟好后綴對齊繼續匹配。
 找到了移動規則
找到了移動規則 -
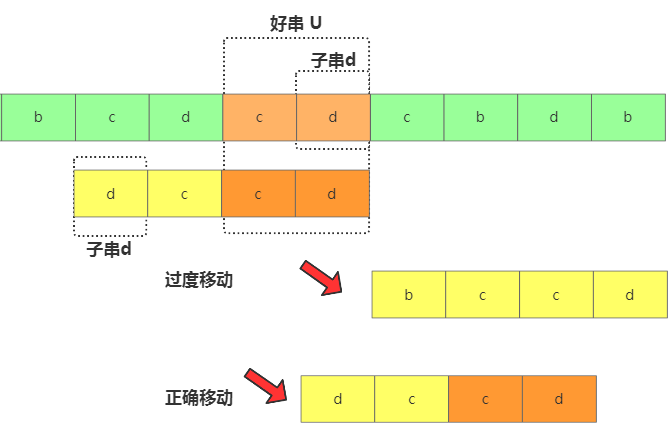
找不到的時候,如果直接移動長度是模式串m位,那極有可能過度了!而過度移動存在的原因就是,比如你找了好后綴u,u在模式串中整體沒找到,但是u的子串d是可以跟模式串匹配上的啊。
 過度移動
過度移動
所以此時還要看好后綴的后綴子串是否跟模式串中的前綴子串匹配,從好后綴串的后后綴子串中找個最長能跟模式串的前綴子串匹配的然后滑動到一起,比如上面的d。
然后分別計算壞字符往后滑動位數跟好后綴往后滑動此時,兩者取其大作為模式串往后滑動位數,這種情況下還可以避免壞字符的負數情況。
3.4 好后綴代碼
好后綴的核心其實就在于兩點:
-
在模式串中,查找跟好后綴匹配的另一個子串。
-
在好后綴的后綴子串中,查找最長的、能跟模式串前綴子串匹配的后綴子串。
3.4.1 預處理工作
上面兩個核心點可以在代碼層面用暴力解決,但太耗時!我們可以在匹配前通過預處理模式串,預先計算好模式串的每個后綴子串,對應的另一個可匹配子串的位置。
先看如何表示模式串中不同的后綴子串,因為后綴子串的最后個字符下標為m-1,我們只需記錄后綴子串長度即可,通過長度可以確定一個唯一的后綴子串。
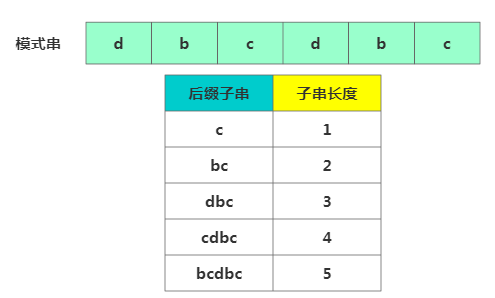 子串表示
子串表示再引入關鍵的變量
suffix數組。suffix 數組的index表示后綴子串的長度。下標對應的數組值存儲的是好后綴在模式串中匹配的起始下標值:
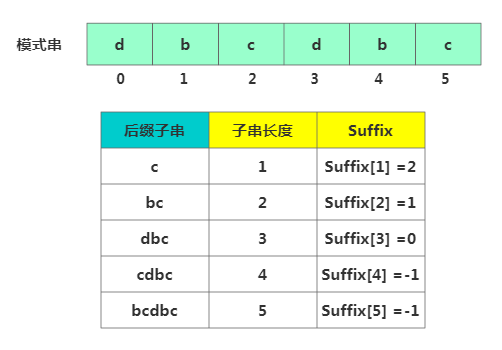 suffix數組定義
suffix數組定義比如此處后綴子串c在模式串中另一個匹配開始位置為2, 后綴子串bc在模式串中另一個匹配開始位置為1 后綴子串dbc在模式串中另一個匹配開始位置為0, 后綴子串cdbc在模式串中只出現了一次,所以為-1。
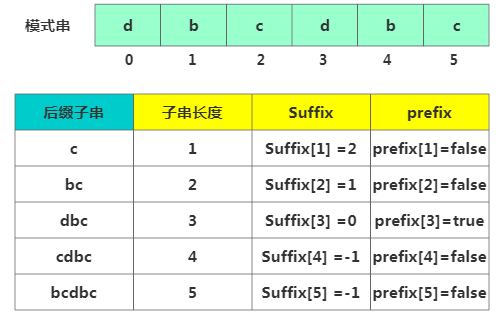 prefix 數組
prefix 數組這里需注意,我們不僅要在模式串中查找跟好后綴匹配的另一個子串,還要在好后綴的后綴子串中查找最長的能跟模式串前綴子串匹配的后綴子串。比如下面:
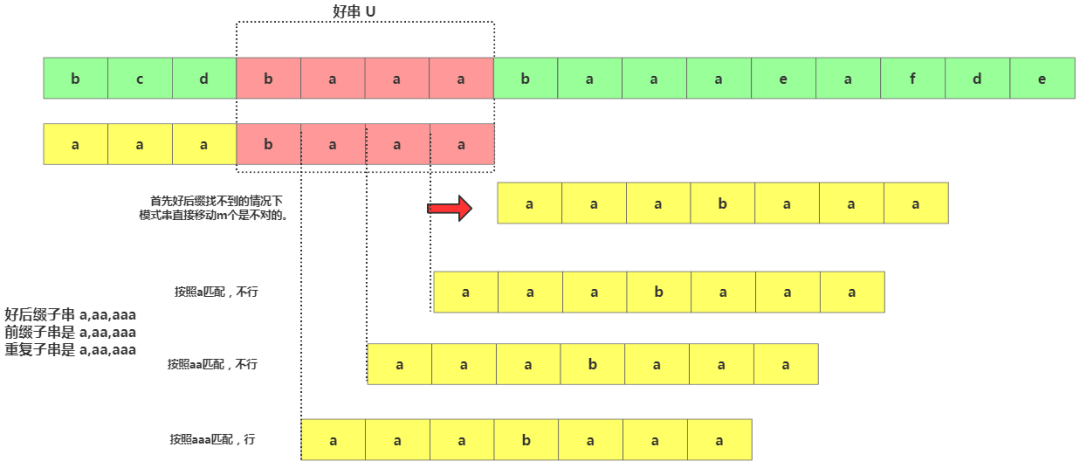 最長模式匹配
最長模式匹配
用suffix只能查找跟好后綴匹配的另一個子串。但還需要個 boolean 類型的prefix數組來記錄模式串的后綴子串是否能匹配模式串的前綴子串。
接下來重點看下如何填充suffix跟prefix數組,拿下標從 0 到 i 的子串與整個模式串,求公共后綴子串,其中i=[0,m-2]。如果公共后綴子串的長度是 k,就suffix[k]=j,其中 j 表示公共后綴子串的起始下標。如果 j = 0,說明公共后綴子串也是模式串的前綴子串,此時 prefix[k]=true。
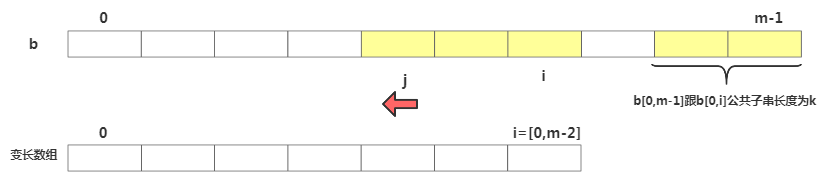 suffix跟prefix數組
suffix跟prefix數組
//b=模式串,m=模式串長度,suffix,prefix數組如上定義
privatevoidgenerateGS(char[]b,intm,int[]suffix,boolean[]prefix){
//初始化
for(inti=0;ii++){
suffix[i]=-1;
prefix[i]=false;
}
//b[0,i]
for(inti=0;i1;i++){
intj=i;
//公共后綴子串長度
intk=0;
//與b[0, m-1]求公共后綴子串,并且會有覆蓋現象產生。
while(j>=0&&b[j]==b[m-1-k]){
--j;
++k;
//j+1表示公共后綴子串在b[0,i]中的起始下標
suffix[k]=j+1;
}
//如果公共后綴子串也是模式串的前綴子串
if(j==-1)prefix[k]=true;
}
}
3.4.2 正式代碼
有了suffix跟prefix數組后,看下移動規則。假設好后綴串長度=k,如果k != 0,說明有好后綴,接下來通過suffix[k]的值來判斷如何移動。
-
suffix[k] != -1,不等于時說明匹配上了,模式串后移 j-suffix[k]+1 位,其中 j 表示壞字符對應的模式串中的字符下標。
-
suffix[k] = -1,等于時說明好后綴沒匹配上,那就看下子串的匹配情況,好后綴的后綴子串長度是 b[r, m-1],其中 r = [j+2,m-1],后綴子串長度 k=m-r,如果 prefix[k] = true,說明長度為 k 的后綴子串有可匹配的前綴子串,這樣我們可以把模式串后移 r 位。
-
如果都沒匹配上,那就直接將模式串后移m位。
// a跟n 分別表示主串跟主串長度。 // b跟m 分別表示模式串跟模式串長度。 publicintbm(char[]a,intn,char[]b,intm){ //用來記錄模式串中每個字符最后出現的位置 int[]sl=newint[SIZE]; //構建壞字符哈希表 generateBC(b,m,sl); int[]suffix=newint[m]; boolean[]prefix=newboolean[m]; //構建suffix跟prefix數組 generateGS(b,m,suffix,prefix); inti=0;//j表示主串與模式串匹配的第一個字符 while(i<=?n?-?m)?{ ????intj; //模式串從后往前匹配 for(j=m-1;j>=0;--j){ //壞字符對應模式串中的下標是j if(a[i+j]!=b[j])break; } if(j0){ //匹配OK,返回主串與模式串第一個匹配的字符的位置 returni; } //壞字符計算所得需移動長度 intx=j-sl[(int)a[i+j]]; inty=0; //j if(j-1){ y=moveByGS(j,m,suffix,prefix); } i=i+Math.max(x,y); } return-1; } //j=壞字符對應的模式串中的字符下標 //m=模式串長度 privateintmoveByGS(intj,intm,int[]suffix,boolean[]prefix){ //好后綴長度 intk=m-1-j; if(suffix[k]!=-1){ //好后綴可以匹配上,返回需移動長度 returnj-suffix[k]+1; } //有匹配到好后綴子串的模式串前綴子串 for(intr=j+2;r<=?m-1;++r){ if(prefix[m-r]==true){ returnr; } } //沒找到直接移動最大值 returnm; }
3.5 復雜度分析
整個BM算法用到了額外的 sl、suffix、prefix三個數組,其中sl數組大小跟字符集大小有關,suffix 數組和 prefix 數組的大小跟模式串長度 m 有關。如果處理字符集很大的字符串匹配問題,bc 數組對內存的消耗就會比較多。
因為好后綴和壞字符規則是獨立的,如果我們運行的環境對內存要求苛刻,可以只使用好后綴規則,不使用壞字符規則,這樣就可以避免 bc 數組過多的內存消耗。不過,單純使用好后綴規則的 BM 算法效率就會下降一些了。
BM 算法的時間復雜度分析起來是非常復雜,一般在3n~5n之間。
4 KMP 算法
KMP算法跟BM算法類似,從前往后匹配,把能匹配上的叫好前綴,不能匹配上的叫壞字符。
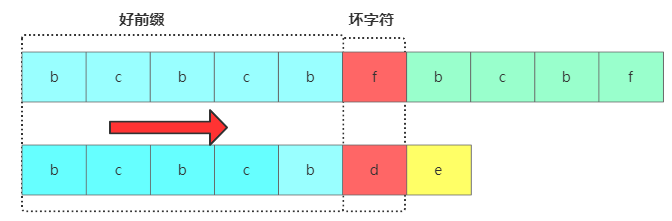 KMP匹配定義
KMP匹配定義遇到壞字符后就要進行主串好前綴后綴子串跟模式串的前綴子串進行對比,問題是對于已經比對過的好前綴,能否找到一種規律,將模式串一次性滑動很多位?
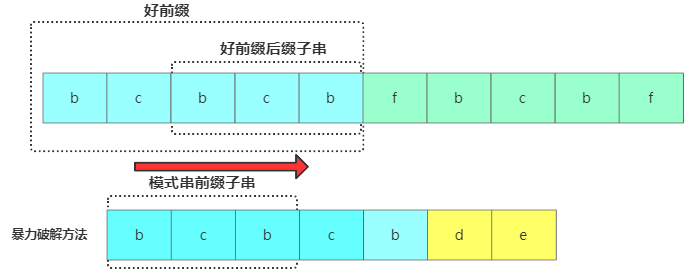 暴力破解
暴力破解
思路是將主串中好前綴的后綴子串和模式串中好前綴的前綴子串進行對比,獲取模式串中最大可以匹配的前綴子串。一般把好前綴的所有后綴子串中,最長的可匹配前綴子串的那個后綴子串,叫作最長可匹配后綴子串。對應的前綴子串,叫作最長可匹配前綴子串。假如現在最長可匹配后綴子串 = u,最長可匹配前綴子串 = v,獲得u跟v的長度為k,此時在主串中壞字符位置為i,模式串中為j,接下來將模式串后移j-k位,然后將待比較的模式串位置j = j-k進行比較。
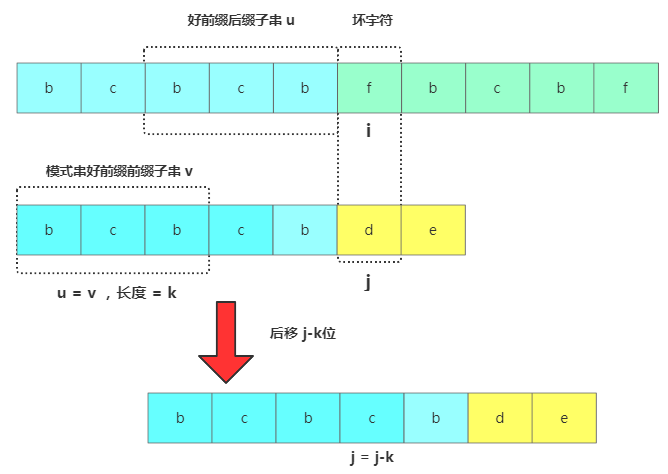 KMP算法移動
KMP算法移動4.1 Next 數組存在意義
那最長可匹配前綴跟后綴我們用模式串就可以求解了。仿照BM算法,預先計算好就行。在KMP算法中提前構造個next數組。其中next數組的下標用來存儲前綴子串最后一個數據的index,對應的value保存的是這個字符串的后綴子串集合跟前綴子串集合的交集。
干說可能不太好理解,我們以"abababca"為例。它的部分匹配表(Partial Match Table)數組如下:
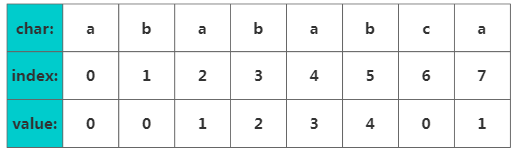 Next數組
Next數組接下來對value值的獲取進行解釋,如果字符串A和B,存在A=BS,其中S是任意的非空字符串,那就稱B為A的前綴。例如”what”的前綴包括{"w","wh","wha"},我們把所有前綴組成的字符串的前綴集合。同樣可以定義后綴A=SB, 其中S是任意的非空字符串,那就稱B為A的后綴,例如"Potter"的后綴包括{"otter", "tter", "ter", "er", "r"},然后把所有后綴組成字符串的后綴集合。要注意字符串本身并不是自己的后綴。
PMT數組中的值是字符串的前綴集合與后綴集合的交集中最長元素的長度。例如,對于"aba",它的前綴集合為{"a", "ab"},后綴集合為{"ba", "a"}。兩個集合的交集為{"a"},那么長度最長的元素就是字符串"a"了,長度為1,所以"aba"的Next數組value = 1,同理對于"ababa",它的前綴集合為{"a", "ab", "aba", "abab"},它的后綴集合為{"baba", "aba", "ba", "a"}, 兩個集合的交集為{"a", "aba"},其中最長的元素為"aba",長度為3。
我們以主串"ababababca"中查找模式串"abababca"為例,如果在j處字符不匹配了,那在模式串[0,j-1]的數據串"ababab"中,前綴集合跟后綴集合的交集最大值就是長度為4的"abab"。
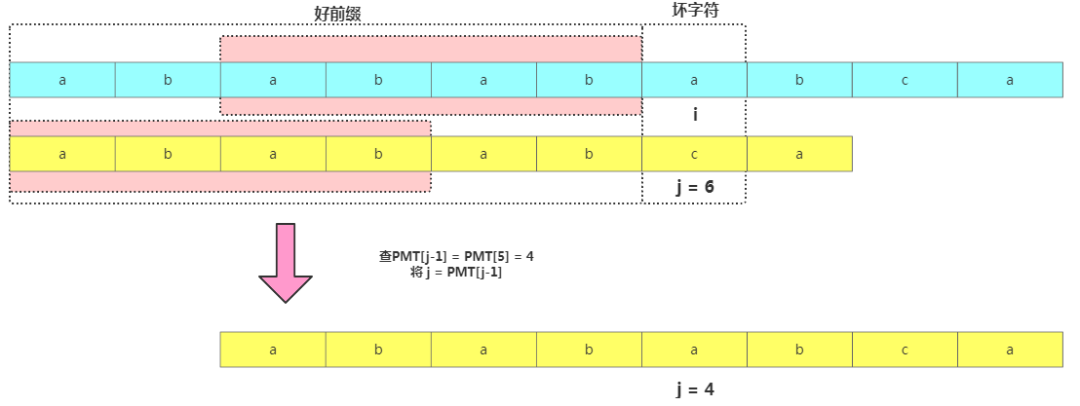 PMT數組使用方法
PMT數組使用方法基于此就可以使用PMT加速字符串的查找了。我們看到如果是在
j位失配,那么影響j 指針回溯的位置的其實是第 j?1 位的 PMT 值,但是編程中為了方便一般不直接使用PMT數組而是使用Next數組,Next數組的value其實就是存儲的這個前綴的最長可以匹配前綴子串的結尾字符下標,其中如果匹配不到用-1代替。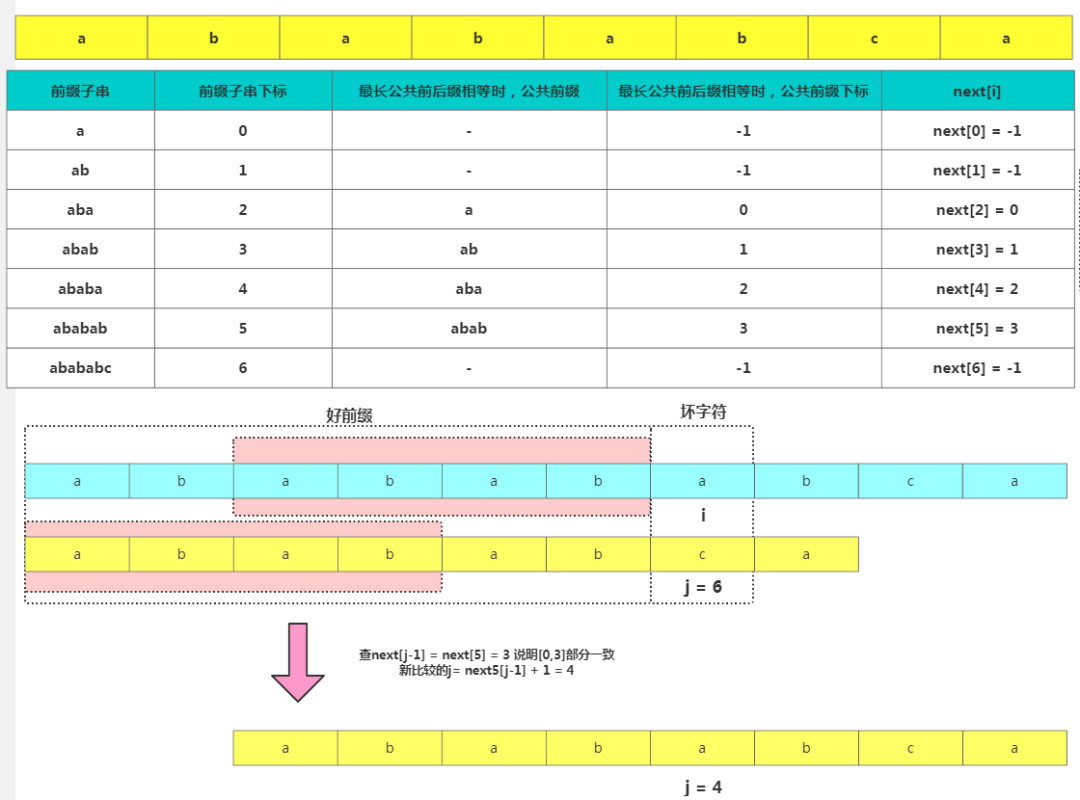 Next數組使用
Next數組使用4.2 KMP 匹配代碼
// a =主串,n=主串長度。b =模式串,m =模式串長度
publicstaticintkmp(char[]a,intn,char[]b,intm){
int[]next=getNexts(b,m);
intj=0;
for(inti=0;iwhile(j>0&&a[i]!=b[j]){
j=next[j-1]+1;//發現不一樣則保持i不變j進行移動
}
if(a[i]==b[j]){
++j;
}
if(j==m){//找到匹配模式串的了
returni-m+1;
}
}
return-1;
}
至此你會發現只要搞明白了PMT存在的意義,然后順著思路推Next數組即可。
4.3 Next 數組求解
當要計算next[i]時,前面計算過的next[0~i-1]是否可以被用來快速推導出next[i]呢?
情況一:如果next[i-1] = k-1,那此時b[0,i-1]的最長可匹配前綴子串是b[0,k-1],如果b[0,i-1]的下個字符b[i]跟b[0,k-1]的下個字符b[k]相等,那next[i] = k。

情況二:假設b[0,i]最長可用后綴子串是b[r,i],那b[r,i-1]肯定是b[0,i-1]的可匹配后綴子串,但不一定是最長可匹配后綴子串。比如字符串b = "dexdecdexdex",此時最長可匹配后綴子串是"dex",b去掉最后的'x'成為B,此時雖然"de"是B的可匹配后綴子串,但"dexde"才是最長后綴子串!也就是說b[0, i-1]最長可匹配后綴子串對應的模式串的前綴子串的下一個字符并不等于 b[i]。
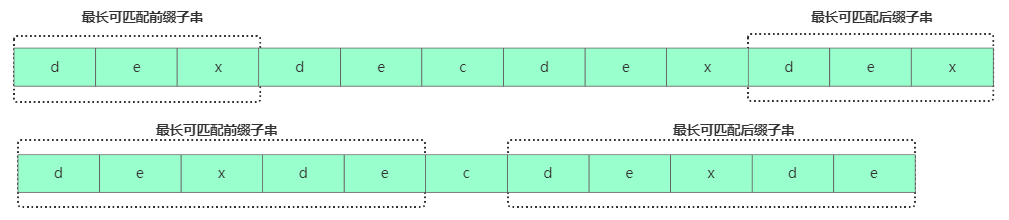
那此時看下b[0,i-1]的
次長可匹配后綴子串b[x,i-1]對應的可匹配前綴子串b[0,i-1-x] 的下個字符b[i-x] 是否等于b[i],相等那b[0,i]的最長可匹配后綴子串是b[x,i]。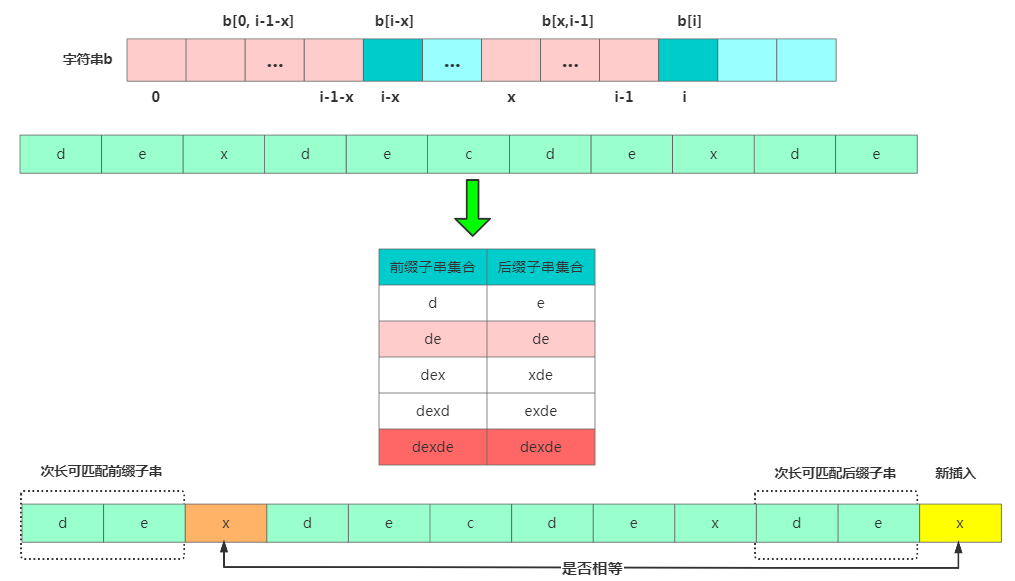
那我們來求 b[0, i-1]的次長可匹配后綴子串呢?次長可匹配后綴子串一定被包含在最長可匹配后綴子串中,而最長可匹配后綴子串又對應最長可匹配前綴子串 b[0, y]。此時查找 b[0, i-1]的次長可匹配后綴子串變成了查找b[0, y]的最長匹配后綴子串的問題。
按此思路考察完所有的 b[0, i-1]的可匹配后綴子串 b[y, i-1],直到找到一個可匹配的后綴子串,它對應的前綴子串的下一個字符等于 b[i],那這個 b[y, i]就是 b[0, i]的最長可匹配后綴子串。
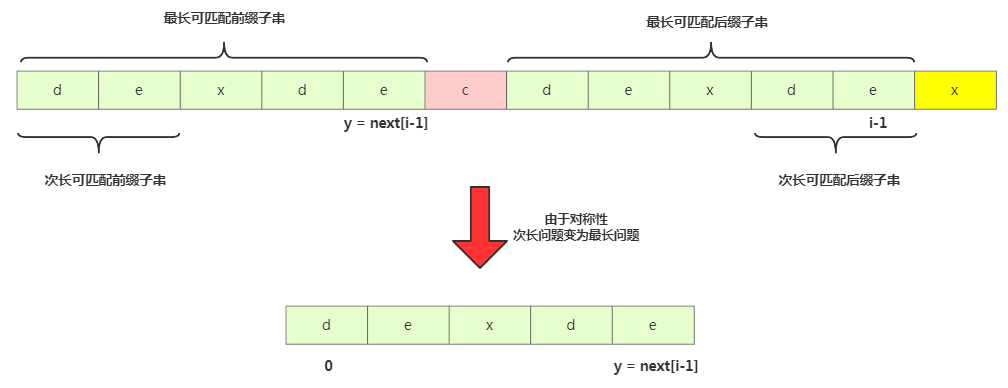
//b=模式串,m=模式串的長度
privatestaticint[]getNexts(char[]b,intm){
int[]next=newint[m];
next[0]=-1;
intk=-1;
for(inti=1;iwhile(k!=-1&&b[k+1]!=b[i]){
k=next[k];
//因為前一個的最長串的下一個字符不與最后一個相等,需要找前一個的次長串,
//問題就變成了求0到next(k)的最長串,如果下個字符與最后一個不等,
//繼續求次長串,也就是下一個next(k),直到找到,或者完全沒有
//最好結合前面的圖來看
}
if(b[k+1]==b[i]){
++k;//字符串相等則看下一個
}
next[i]=k;//數組賦值
}
returnnext;
}
KMP空間復雜度:該算法只需要一個額外的 next 數組,數組的大小跟模式串相同。所以空間復雜度是 O(m),m 表示模式串的長度。
KMP時間復雜度:next 數組計算的時間復雜度是 O(m) + 匹配時候時間復雜度是 O(n) = O(m+n)
至此,常見的字符串匹配算法正式講解完畢,其實前面說的都是一個主串,一個模式串。
審核編輯 :李倩
-
字符串
+關注
關注
1文章
584瀏覽量
20552
原文標題:字符串硬核講解
文章出處:【微信號:zhuyandz,微信公眾號:FPGA之家】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 關于字符串硬核講解
關于字符串硬核講解













評論