emmmmm,好長時間沒有用matplotlib，都不會畫圖了。先繪制一個x**3-1的函數，然后考慮在a,b之間找他的根。

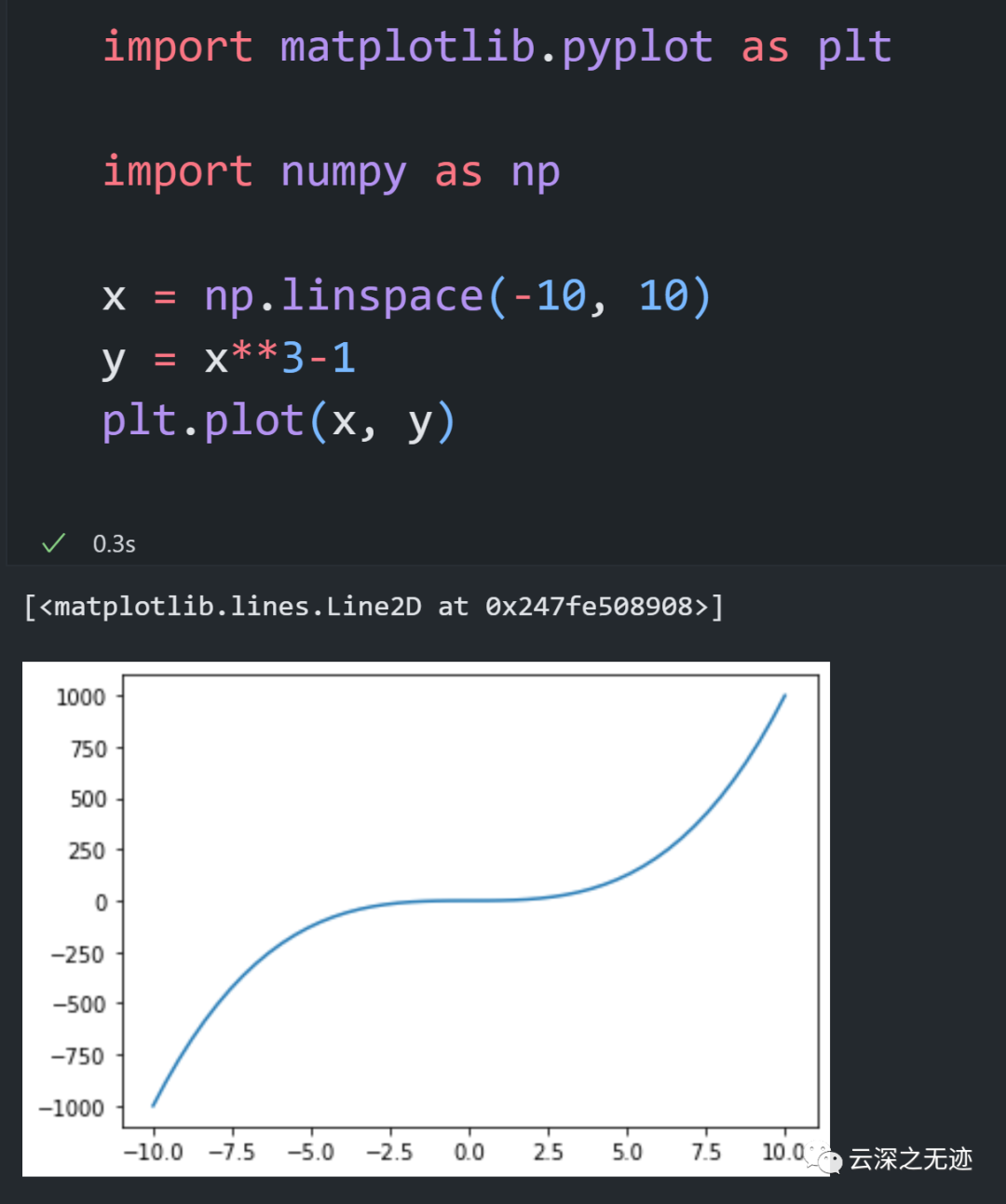
-10，10

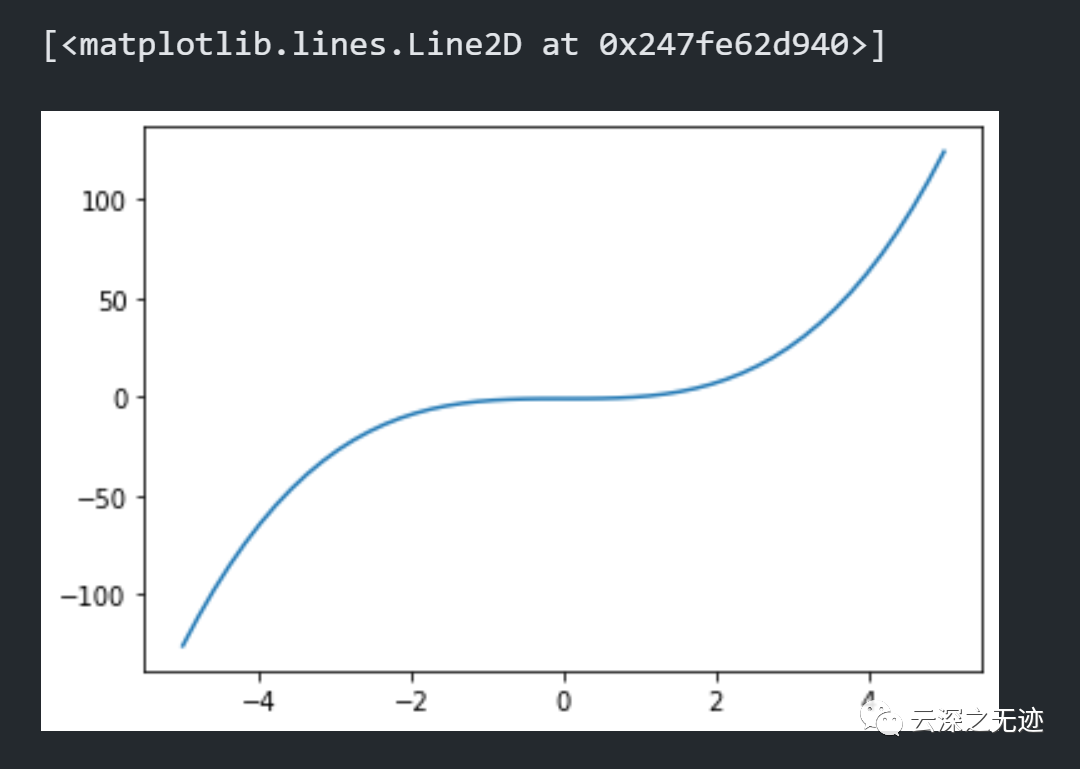
-5，5

那么這個函數被起名為intersection

連續函數與x相交時就是根，是不是很形象。

def intersection(function: Callable[[float], float], x0: float, x1: float) -> float:

因為我們知道，這個函數應該是我們給出要求解的區間和函數給出一個根。那么這里function的Callable就是可以當匿名函數傳遞。

為了函數的靈活性，這里使用float

主函數，因為我們函數其實不知道具體的函數的循環次數，那么就可以使用while的循環。

一開始要判斷參數的情況，如果都相等，你這算啥？？？以及都帶進去，再算一下，雙保險，雙重撲街。

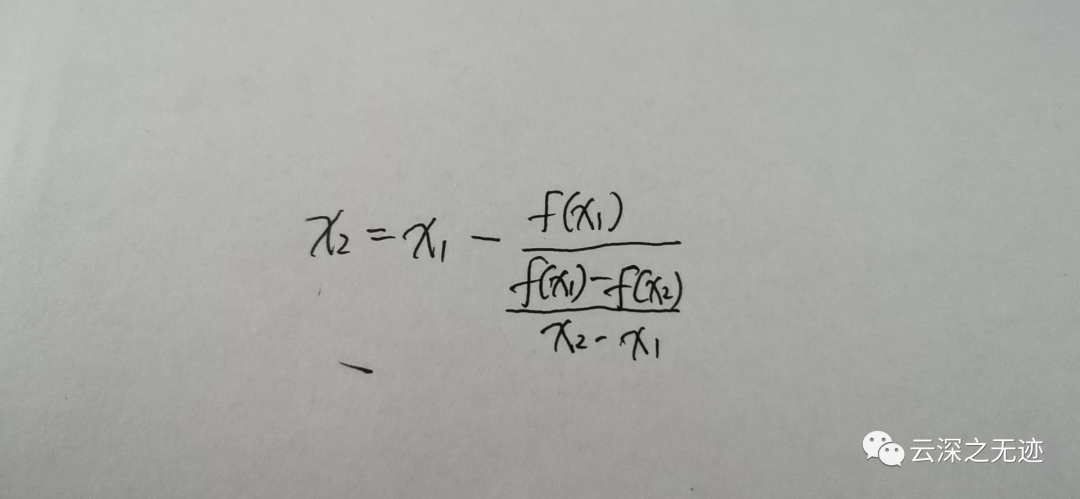
接下來就是這個公式，我是個罪人，用了一張A4紙就寫一個這

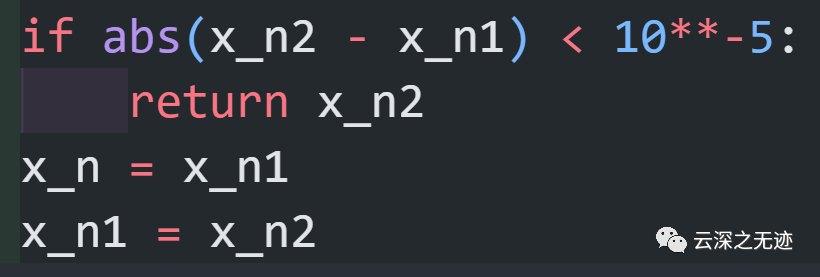
計算的X看看符合要求嗎？不符合就繼續將值域縮小。直到很小。

這個不是二分法，但是差不多的意思，不過這個是牛頓法，也叫牛頓-拉夫遜（拉弗森）方法，就我的題目。

這篇文章的下面就講講這個東西：

它是牛頓在17世紀提出的一種在實數域和復數域上近似求解方程的方法。

多數方程不存在求根公式，因此求精確根非常困難，甚至不可解，從而尋找方程的近似根就顯得特別重要。方法使用函數 f(x) 的泰勒級數的前面幾項來尋找方程 f(x)=0 的根。牛頓迭代法是求方程根的重要方法之一，其最大優點是在方程 f(x)=0 的單根附近具有平方收斂，而且該法還可以用來求方程的重根、復根，此時線性收斂，但是可通過一些方法變成超線性收斂。

牛！

迭代法也稱輾轉法，是一種不斷用變量的舊值遞推新值的過程，跟迭代法相對應的是直接法（或者稱為一次解法），即一次性解決問題。迭代算法是用計算機解決問題的一種基本方法。它利用計算機運算速度快、適合做重復性操作的特點，讓計算機對一組指令（或一定步驟）重復執行，在每次執行這組指令（或這些步驟）時，都從變量的原值推出它的一個新值。

利用迭代算法解決問題，需要做好以下三個方面的工作：

一、確定迭代變量

在可以用迭代算法解決的問題中，至少存在一個可直接或間接地不斷由舊值遞推出新值的變量，這個變量就是迭代變量。

二、建立迭代關系式

所謂迭代關系式，指如何從變量的前一個值推出其下一個值的公式（或關系）。迭代關系式的建立是解決迭代問題的關鍵，通常可以使用遞推或倒推的方法來完成。

三、對迭代過程進行控制

在什么時候結束迭代過程？這是編寫迭代程序必須考慮的問題。不能讓迭代過程無休止地執行下去。迭代過程的控制通常可分為兩種情況：一種是所需的迭代次數是個確定的值，可以計算出來；另一種是所需的迭代次數無法確定。對于前一種情況，可以構建一個固定次數的循環來實現對迭代過程的控制；對于后一種情況，需要進一步分析得出可用來結束迭代過程的條件。

然后，自己的函數也可以這樣定義

intersection(f, 3, 3.5)

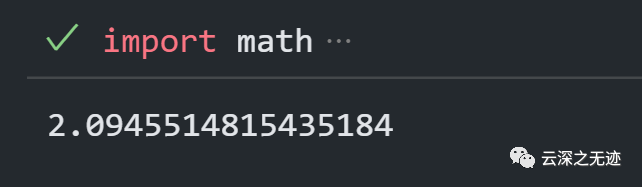
精度ok

再說說數值求法：

大多數的數值求根算法都使用迭代法，生成一個以方程的根為極限的收斂數列。它們需要一個或多個根作為迭代的初期值，之后每次迭代都生成一個逐步逼近根的值。

由于迭代法必須在有限步內終止于某個點，這些方法都只能提供一個根的近似值，而不能提供一個精確解。許多方法是通過代入上一個迭代值來計算一個輔助方程，從而得出下一個迭代值的。此處所指的輔助方程是指為了使原方程的根是一個定點并使迭代值能更快地收斂到這些定點而設計的一個方程，因此迭代值的極限是這個輔助方程的一個定點。

求根算法的性能是數值分析的研究范疇。一種算法的效率可能大幅度取決于已知點的性質。

例如，一部分算法都使用輸入函數的導數（此要求函數不但連續，而且可導），而其他算法則能用于任何一個連續函數。在一般情況下，數值算法不能保證找到一個函數的所有根，因此算法未能找到根并不能證明方程無根。然而，對于多項式，存在特定的使用代數學性質以定位根的所在區間（或復根所在的圓盤）的算法，這個區間（或圓盤）足夠小以能保證數值算法（例如牛頓法）能收斂到唯一被定位的根。