傳統顯著性檢驗用于推斷樣本所代表的總體均值是否相等，它的檢驗假設為樣本來自同一總體(即總體均值相等)。在應用中，顯著性檢驗結果不能評價差別的大小，也不能說明差別是否有實際意義，所謂差別顯著是指在統計學理論上認為樣本來自不同的總體。另外顯著性檢驗在均值差異性比較中也存在一定的局限性，下面我們以雙樣本t檢驗為例來說明。

顯著性檢驗的局限性

我們看到下表1中兩種測試方法得到的數據，希望比較兩種測試方法得到的結果是否一致（等效）。

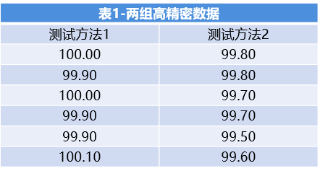
可能首先想到的方法就是用雙樣本t檢驗，我們來試試看（前提條件驗證略）。

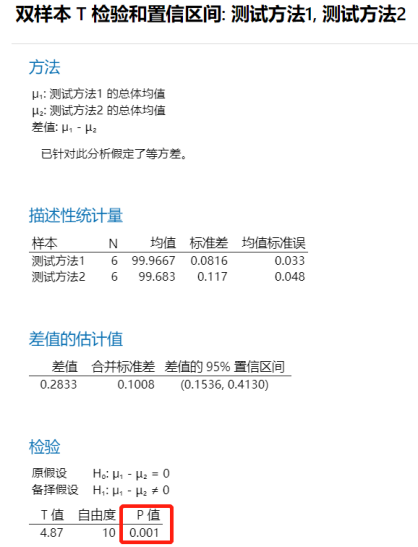
雙樣本t檢驗的結果顯示，P=0.001＜0.05，所以我們得到的結論是：兩種測試方法的結果是有顯著性差異的。拒絕是有說服力的，所以我們也不用擔心犯第二類錯誤。

現在我們再來看看下表2中兩種測試方法的數據，也想來比較有沒有顯著性差異。

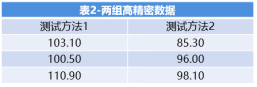
同理，我們也來執行雙樣本t檢驗（前提條件驗證略），得到如下結果。

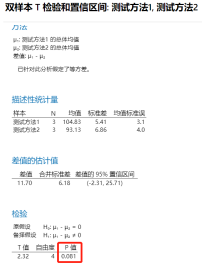
雙樣本t檢驗的結果顯示，P=0.081＞0.05，所以我們得到的結論是：兩種測試方法的結果無顯著性差異的，即不拒絕原假設。不拒絕是沒有說服力的，可能是樣本量不夠導致的（建議做功效與樣本量的計算）。

基于以上分析，總結如下：

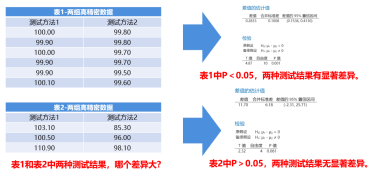
但是，如果你仔細去看一看表1和表2中的數據，有沒有發現表1中兩種測試方法結果差異比較小（但雙樣本t檢驗結果P=0.001＜0.05），表2中兩種測試方法結果差異比較大（但雙樣本t檢驗結果P=0.081＞0.05），注意，這不是錯覺，這是t檢驗本身存在的局限性。

為什么這么說，我們以表2中數據（兩總體標準差未知但相等）為例來看看t檢驗的基本原理。

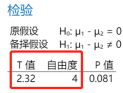
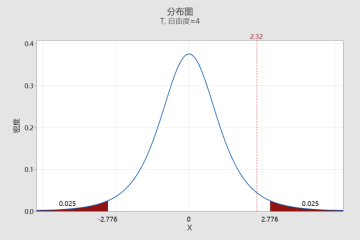
T=2.32小于拒絕域臨界值2.776，及檢驗統計量T落在非拒絕域（白色區域），故不拒絕原假設。換句話說，如果想拒絕原假設（得到兩種測試方法有顯著差異的結論），就需要檢驗統計量T值（絕對值）足夠大，大到超過2.776，那么怎么做才能實現呢？通過后臺公式我們能發現只需要：樣本量足夠大且/或合并標準差SP足夠小。

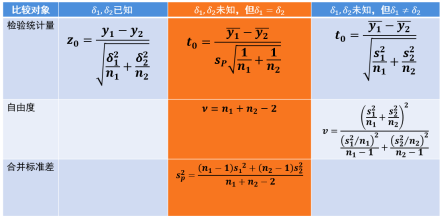
其實這是一個有悖邏輯的發現，因為如果真的如此的話，那我以后直接選擇擺爛不就可以嗎（樣本量少抽一點，測量變異搞大點，這樣越不容易得到有顯著差異）。

等價檢驗

從功能和實用意義上來講，產品之間存在微小差異并不總是十分重要。例如，在200 mg的藥物劑量中，相差1mg不會產生任何實際效應，那如果我想證明藥物劑量不同對療效是相同的或相近的，又該如何去驗證呢？可不可以用顯著性檢驗的方法（如t檢驗）？

顯著性檢驗確定備擇假設的方法是“想證明什么結論就把它放在備擇假設上”，那能否把相等的結論放在備擇假設上，如H0：μ≠μ0， H1: μ＝μ0很遺憾，統計學中不可能處理這種“原假設是某個范圍，而備擇假設只是一個單點”的情況，只能處理備擇假設為

H1:|μ-μ0|<△

H1: μ1<μ<μ2

其中μ1=μ0-△，μ2=μ0+△

這類檢驗問題稱為等價檢驗（equivalence test）問題，也稱等效性檢驗問題。其中（μ1，μ2）稱為等價區間。它的原假設和備擇假設為：

H0:μ<μ1或μ>μ2 H1:μ1≤μ≤μ2

等價檢驗實際上是雙單側假設檢驗（TOST），當左右兩邊的原假設同時被拒絕時才能認為原假設不成立。

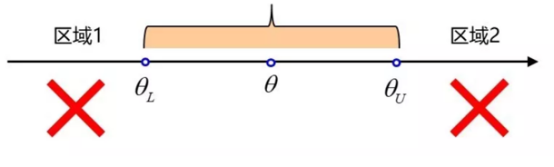
等價檢驗 VS 顯著性檢驗

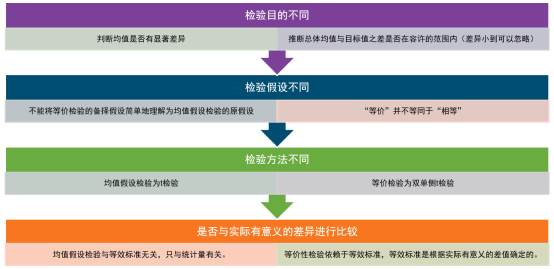
等價檢驗與顯著性檢驗比較如上圖，下面我們通過一個具體案例來說明一下（案例來自于藍皮書第三版P161）。

示例：在焊接電路板的過程中，焊錫膏的涂抹厚度是關鍵的控制量之一。工藝標準要求涂抹厚度的均值是60微米，均值偏差在5微米內。現在收集了25個焊點上的焊錫膏涂抹厚度。我們希望驗證，涂抹厚度均值是60微米嗎？涂抹厚度均值是落在（55,65）之內嗎？

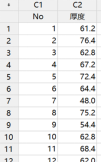
我們先來看看如果是用顯著性檢驗（單樣本t檢驗）會得到什么結果。

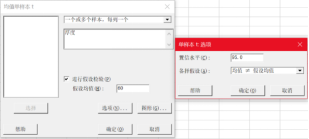
由于P值為0.111，因此無法拒絕原假設，也就是說沒有充分的理由否認焊錫膏涂抹厚度均值為60。但“不否認”還不是明確的說明“均值就是60微米”的有說服力的結論。如果需要進一步確定“均值就是60微米”，或者更進一步判斷其均值是否落入（55,65），則只能使用單樣本等價檢驗方法（注意：即使是等價檢驗對于備擇假設只是一個單點也是無能為力的）。

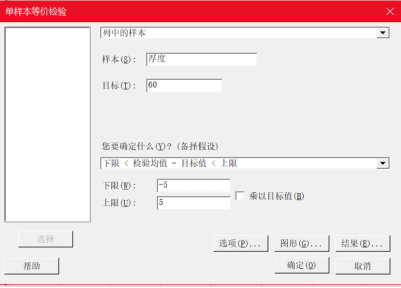
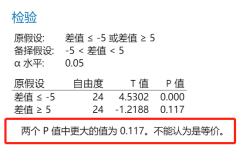
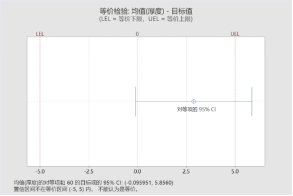
正如Minitab告訴你的，不能認為是等價的，即焊錫膏涂抹厚度均值可以認為是60微米，但未落在（55，65）之內，即精確度未達到誤差小于5微米的水平。

那如果允許誤差放大些，比如說（50，70），結果就可以認為是等價的了。

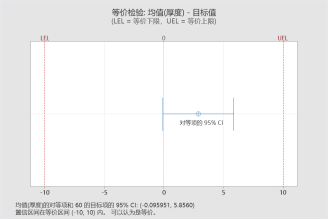
請注意，我在這里不得不說明一下，千萬不要說為了得到等價的結論而去改等價區間，我在這里修改只是為了說明問題，我們在實際工作一定是要事先指定好等價區間范圍（防止扯皮）。

小結

要在等價檢驗和標準t檢驗之間進行選擇，請考慮您希望證明或說明的內容。如果您希望證明兩個均值相等或者證明均值等于目標值，而且您可以確切地定義在所屬領域中屬于重要差值的差值大小，則您可能希望使用等價檢驗，而不是標準t檢驗。

審核編輯 黃昊宇