上世紀九十年代，斯坦福大學的知名生物信息學教授 Rob Tibshirani 曾擬了一個詞匯表，將機器學習與統計學中的不同概念作了簡單而粗暴的對應關系：

一方面，這個表格為理解機器學習提供了基礎的認識，但同時，其簡單地將深度學習或機器學習中的概念歸納為統計學中的詞義，也引起了大多數人對深度學習本質的認知偏差：即深度學習是“簡單的統計”。

然而，在深入探討中，這樣的認知在一定程度上阻礙了研究者理解深度學習成功的本質原因。在今年六月的一篇文章“The uneasy relationship between deep learning and (classical) statistics”中，哈佛大學知名教授、理論計算機科學家 Boaz Barak 就將深度學習與統計學進行了對比區分，指出深度學習的根本構成因素就與統計學有諸多不同。

Boaz Barak 提出一個重要的觀察：從模型的用途來看，如果是側重預測與觀察，那么具備黑匣子特性的深度學習模型可能是最好的選擇；但如果是希望獲取對事物的因果關系理解、提高可解釋性，那么“簡單”的模型可能表現更佳。這與馬毅、曹穎、沈向洋三位科學家在上個月提出的構成智能兩大原理之一的“簡約性”見解不謀而合。

與此同時，Boaz Barak 通過展示擬合統計模型和學習數學這兩個不同的場景案例，探討其與深度學習的匹配性；他認為，雖然深度學習的數學和代碼與擬合統計模型幾乎相同，但在更深層次上，深度學習中的極大部分都可在“向學生傳授技能”場景中被捕獲。

統計學習在深度學習中扮演著重要的角色，這是毋庸置疑的。但可以肯定的是，統計角度無法為理解深度學習提供完整的畫面，要理解深度學習的不同方面，仍需要人們從不同的角度出發來實現。

下面是 Boaz Barak 的論述：

幾千年來，科學家們一直在為觀測結果擬合模型。比如在科學哲學書皮中所提到的，埃及天文學家托勒密提出了一個巧妙的行星運動模型。托勒密的模型是地心的（即行星圍繞地球旋轉），但有一系列“旋鈕”（knobs，具體來說就是“本輪”），使其具有出色的預測準確性。相比之下，哥白尼最初的日心說模型則是假設行星圍繞太陽的圓形軌道。它比托勒密的模型更簡單（“可調節旋鈕”更少）、且整體上更正確，但在預測觀察方面卻不太準確。（哥白尼在后來也添加了他自己的本輪，從而與托勒密的表現可以相媲美。）

托勒密和哥白尼的模型是無與倫比的。當你需要一個“黑匣子”來進行預測時，那托勒密的地心模型更勝一籌。而如果你想要一個可以“窺視內部”的簡單模型，并作為解釋星星運動的理論起點，那哥白尼的模型就更好。

事實上，開普勒最終將哥白尼的模型改進為橢圓軌道，并提出了他的行星運動三定律，這使得牛頓能夠使用地球上適用的相同引力定律來解釋它們。為此，至關重要的是，日心模型并不僅是一個提供預測的“黑匣子”，而是由幾乎沒有“活動部件”的簡單數學方程給出的。多年來，天文學一直是發展統計技術的靈感來源。高斯和勒讓德（獨立地）在 1800 年左右發明了最小二乘回歸，用于預測小行星和其他天體的軌道；柯西在1847年發明的梯度下降，也是受到了天文預測的推動。

在物理學中，（至少有時）你可以“擁有一切”——找到能夠實現最佳預測準確性和數據最佳解釋的“正確”理論，這被諸如奧卡姆剃刀原理之類的觀點所捕捉，假設簡單性、預測能力和解釋性洞察力都是相互一致的。然而在許多其他領域，解釋（或一般情況下稱，洞察力）和預測的雙重目標之間存在張力。如果只是想預測觀察結果，“黑匣子”可能是最好的選擇。但如果你提取因果模型、一般原理或重要特征，那么一個容易理解和解釋的簡單模型可能會更好。

模型的正確選擇取決于其用途。例如，考慮一個包含許多個體的基因表達和表型（比如某種疾病）的數據集，如果其目標是預測個人生病的幾率，往往會希望為該任務使用最佳模型，不管它有多復雜或它依賴于多少基因。相比之下，如果你的目標是在濕實驗室中識別一些基因來進一步研究，那么復雜的黑匣子的用途將是有限的，即使它非常準確。

2001年， Leo Breiman 在關于統計建模兩種文化的著名文章“Statistical Modeling: The Two Cultures”中，就有力地闡述了這一點。“數據建模文化”側重于解釋數據的簡單生成模型，而“算法建模文化 ”對數據是如何產生的并不了解，而是專注于尋找能夠預測數據的模型。Breiman 認為，統計數據太受第一文化的支配，而這種關注“導致了不相關的理論和有問題的科學結論” 和“阻止統計學家研究令人興奮的新問題。”

但是，Breiman 的論文充滿爭議。雖然 Brad Efron 對部分觀點表示贊同，但“看第一遍，Leo Breiman 那篇令人振奮的論文看起來像是反對簡約和科學洞察力，支持很多旋鈕可操縱的黑盒子。而看第二遍，還是那個樣子” 。但在近期一篇文章（“Prediction, Estimation, and Attribution”）中，Efron 大方承認“事實證明，Breiman 比我更有先見之明：純粹的預測算法在 21 世紀占據了統計的風頭，其發展方向與 Leo 此前提到的差不多。”

無論機器學習是否“深度”，它都屬于 Breiman 所說的第二種文化，即專注于預測，這種文化已流傳很長一段時間。例如 Duda 和 Hart 1973 年的教科書《Deconstructing Distributions: A Pointwise Framework of Learning》、以及Highleyman 1962 年《The Design and Analysis of Pattern Recognition Experiments》的論文片段，對于今天的深度學習從業者來說，其辨識度非常高：

同樣地，Highleyman 的手寫字符數據集和被用來與數據集擬合的架構 Chow（準確率約為 58%）也引起了現代讀者的共鳴。

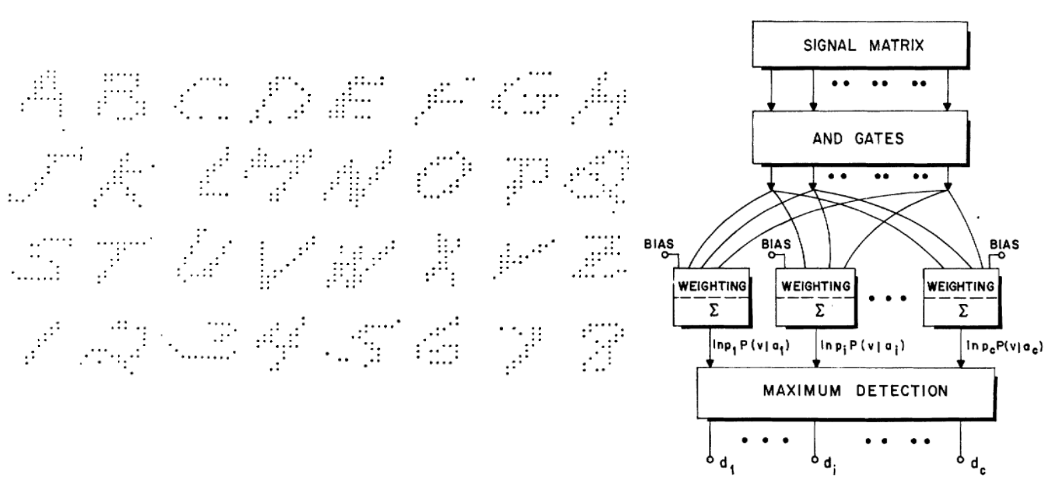
1992 年，Stuart Geman、Elie Bienenstock 和 Rene Doursat 共同寫了一篇題為“Neural Networks and the Bias/Varian Dilemma”的論文，其中談到一些悲觀的看法，例如，“當前的前饋神經網絡，在很大程度上不足以解決機器感知和機器學習中的難題”；具體來說，他們認為通用神經網絡無法成功解決困難的任務，神經網絡成功的唯一途徑是通過手工設計特征。用他們的話來說，即是：“重要的特征必須是內置的或‘硬連線的’(hard-wired）……而不是通過統計的方法來學習。”

事后看來，他們的觀點完全錯了。而且，現代神經網絡的架構如 Transformer 甚至比當時的卷積網絡更通用。但理解他們犯錯的背后原因是很有趣的。

我認為，他們犯錯的原因是深度學習確實與其他學習方法不同。一個先驗的現象是：深度學習似乎只是多了一個預測模型，像最近的鄰居或隨機森林。它可能有更多的“旋鈕”（knobs），但這似乎是數量上而不是質量上的差異。用 PW Andreson 的話來說，就是“more is different”（多的就是不同的）。

在物理學中，一旦規模發生了幾個數量級的變化，我們往往只需要一個完全不同的理論就可以解釋，深度學習也是如此。事實上，深度學習與經典模型（參數或非參數）的運行過程是完全不同的，即使從更高的角度看，方程（和 Python 代碼）看起來相同。

為了解釋這一點，我們來看兩個非常不同例子的學習過程：擬合統計模型，與教學生學習數學。

場景A：擬合統計模型

通常來說，將統計模型與數據進行擬合的步驟如下：

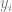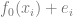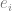1、我們觀察一些數據 x 與y。可將 x 視為一個 n x p 的矩陣，y 視為一個 n 維向量；數據來源于一個結構和噪聲模型：每個坐標的得到形式是，其中是對應的噪聲，為簡單起見使用了加性噪聲，而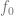是正確的真實標簽。）

2、通過運行某種優化算法，我們可以將模型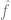擬合到數據中，使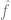的經驗風險最小。也就是說，我們使用優化算法來找到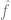的最小化數量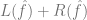，其中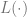是一個損失項（捕捉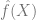距離 y 有多近)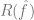，是一個可選的規范化項 （試圖使得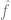偏向更簡單的模型）。

3、我們希望，我們的模型能具有良好的總體損失，因為泛化誤差/損失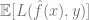很小（這種預測是基于實驗數據所在的總體數據來獲得的）。

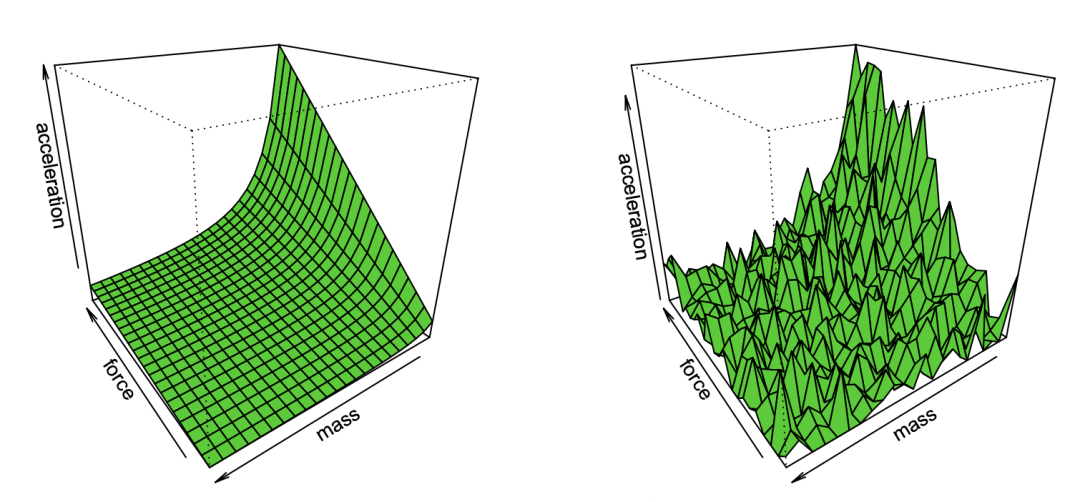
圖注：Bradley Efron經過對噪音的觀察所復現的牛頓第一定律漫畫

這種非常通用的范式包含了許多設置，包括最小二乘線性回歸、最近鄰、神經網絡訓練等等。在經典的統計設置中，我們期望觀察到以下情況：

偏差/方差權衡：將 F 作為優化的模型集。(當我們處于非凸設置和/或有一個正則器項，我們可以讓 F作為這種模型的集合，考慮到算法選擇和正則器的影響，這些模型可以由算法以不可忽略的概率實現。)

F 的偏差是對正確標簽的最佳近似，可以通過元素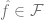來實現。F 的類越大，偏差越小，當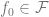，偏差甚至可以是零。然而，當 F 類越大， 則需要越多樣本來縮小其成員范圍，從而算法輸出模型中的方差就越大。總體泛化誤差是偏差項和方差貢獻的總和。

因此，統計學習通常會顯示偏差/方差權衡，并通過正確模型復雜性的“金發姑娘選擇”來最小化整體誤差。事實上，Geman 等人也是這么做的，通過說“偏差-方差困境導致的基本限制適用于包括神經網絡在內的所有非參數推理模型”來證明他們對神經網絡的悲觀情緒是合理的。

更多并非總是最好的。在統計學習中，獲得更多的特征或數據并不一定能提高性能。例如，從包含許多不相關特征的數據中學習更具挑戰性。類似地，從混合模型中學習，其中數據來自兩個分布之一（例如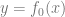和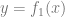），比獨立學習單個更難。

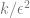收益遞減。在許多情況下，將預測噪聲降低到某個參數，其所需的數據點數量在某些參數 k 下以的形式拓展。在這種情況下，需要大約 k 個樣本來“起飛”，而一旦這樣做，則會面臨收益遞減的制度，即假設花耗 n 個點來達到（比如）90%的準確度，那么想要將準確度提高到95%，則大約需要另外 3n 個點。一般來說，隨著資源增加（無論是數據、模型的復雜性，還是計算），我們希望捕捉到更多更細的區別，而不是解鎖新的質量上的能力。

對損失、數據的強烈依賴。在將模型擬合到高維數據時，一個很小的細節就有可能造成結果的很大不同。統計學家知道，諸如 L1 或 L2 正則化器之類的選擇很重要，更不用說使用完全不同的數據集，不同數量的高維優化器將具有極大的差異性。

數據點沒有自然的“難度”（至少在某些情況下）。傳統上認為，數據點是獨立于某個分布進行采樣的。盡管靠近決策邊界的點可能更難分類，但考慮到高維度的測量集中現象，可預計大多數點的距離將存在相似的情況。因此，至少在經典數據分布中，并不期望點在其難度水平上有很大差異。然而，混合模型可以顯示這種差異的不同難度級別，所以與上述其他問題不同，這種差異在統計設置中不會非常令人驚訝。

場景B：學習數學

與上述相反，我們來談談教學生一些特定的數學題目（如計算導數），給予他們常規指導及要做的練習。這不是一個正式定義的設置，但可考慮它的一些定性特征：

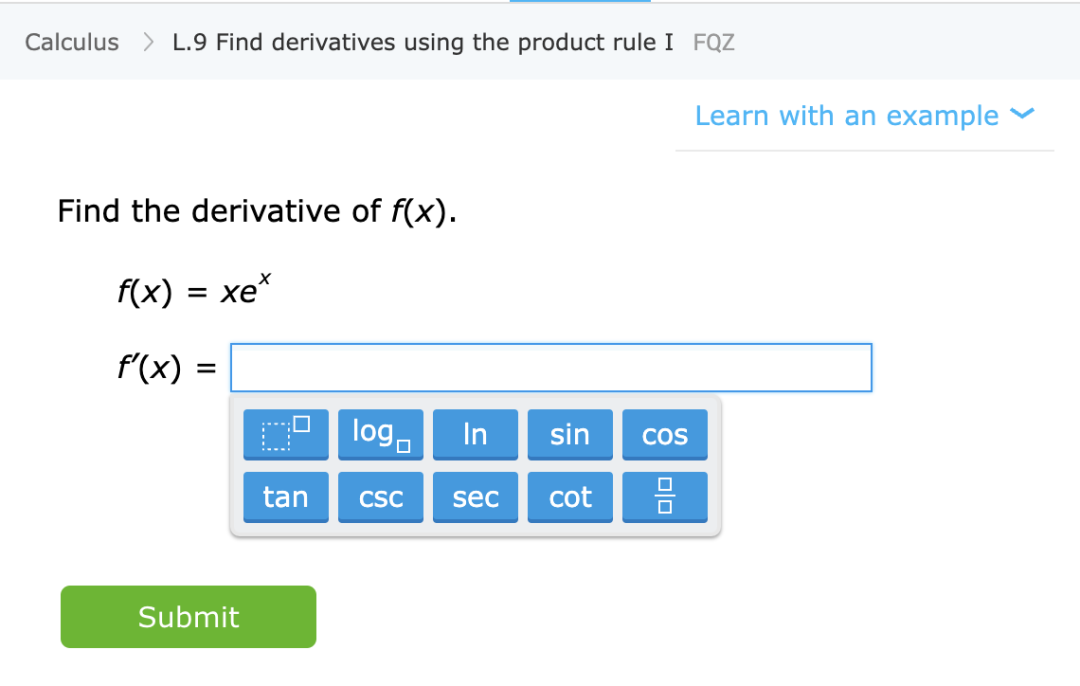
圖注：從IXL 網站學習特定數學技能的練習

學習一項技能，而不是近似分布。在這種情況下，學生是學習一種技能，而非某個數量的估計器/預測器。雖然定義“技能”不是一項微不足道的任務，但卻是一個性質不同的目標。特別是，即使函數映射練習不能用作解決某些相關任務 X 的“黑匣子”，但我們相信，學生在解決這些問題時所形成的內部表征，仍是對 X 有用的。

越多越好。一般來說，學生練習更多問題和不同類型問題，會取得更好的成績。但事實上，“混合模型”——做一些微積分問題和代數問題——不會影響學生在微積分上的表現，反而會幫助他們學習。

“探索”或解鎖功能，轉向自動表示。雖然在某些時候解決問題也會出現收益遞減，但學生似乎確實經歷了幾個階段，有的階段做一些問題有助于概念“點擊”并解鎖新功能。另外，當學生們重復某一特定類型的問題時，他們似乎將自己的能力和對這些問題的表述轉移至較低的水平，使他們能夠對這些問題產生某些以前所沒有的自動性。

性能部分獨立于損失和數據。教授數學概念的方法不止一種，即使學生使用不同書籍、教育方法或評分系統學習，但最終仍可學習到相同的材料和相似的內部表示。

一些問題更難。在數學練習中，我們經常可以看到不同學生在解決同一個問題時所采取的方法存在很強的相關性。一個問題的難度似乎是固定的，解決難題的順序也是固定的，這就使學習的過程能夠優化。這事實上也是IXL等平臺正在做的事情。

那么，上述兩個比喻中，哪個更恰當地描述了現代深度學習，特別是它如此成功的原因呢？統計模型擬合似乎更符合數學和代碼。實際上，規范的 Pytorch 訓練循環，就是通過如上所述的經驗風險最小化來訓練深度網絡的：

然而，在更深層次上，這兩種設置之間的關系并不那么清楚。具體而言，可以通過修復一個特定的學習任務來展開，使用“自監督學習 + 線性探頭（linear probe）”的方法訓練分類算法，其算法訓練如下：

1、假設數據是一個序列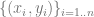，其中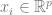是某個數據點（例如具體的圖像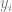）、是一個標簽。

2、首先找到一個深度神經網絡來表示函數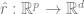，這個函數的訓練只使用數據點而不使用標簽，通過最小化某種類型的自監督損失函數。這種損失函數的例子是重建或畫中畫（從另一個輸入 x 的某些部分恢復）或對比學習（找到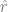使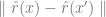顯著更小，當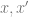是同一個數據點的增量時，并列關系比兩個隨機點的并列關系要小得多）。

3、然后我們使用完整的標記數據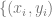來擬合線性分類器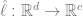（其中 C 是類的數量），使交叉熵損失最小。最終的分類器得出了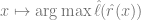的映射。

第 3 步僅適合線性分類器，因此“魔法”發生在第 2 步（深度網絡的自監督學習）。在自監督學習中，可以看到的一些屬性包括：

學習一項技能，而不是逼近一個函數。自監督學習不是逼近一個函數，而是學習可用于各種下游任務的表示。假設這是自然語言處理中的主導范式，那么下游任務是通過線性探測、微調還是提示獲得，都是次要的。

越多越好。在自監督學習中，表征的質量隨著數據量的增加而提高。而且，數據越多樣越好。

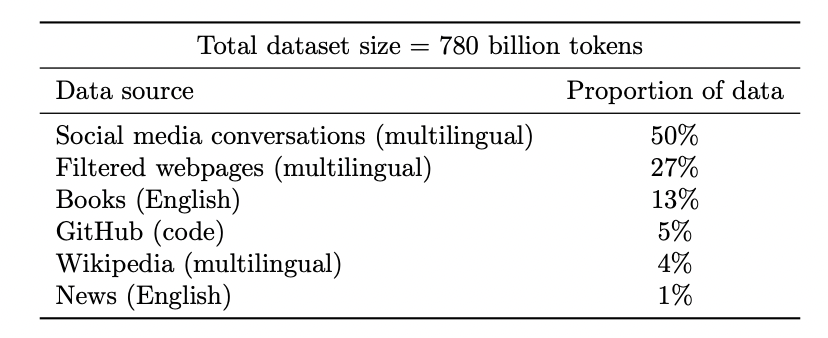
圖注：谷歌 PaLM 模型的數據集

解鎖能力。隨著資源（數據、計算、模型大小）的拓展，深度學習模型的不連續改進一次又一次地被看到，這在一些合成環境中也得到了證明。

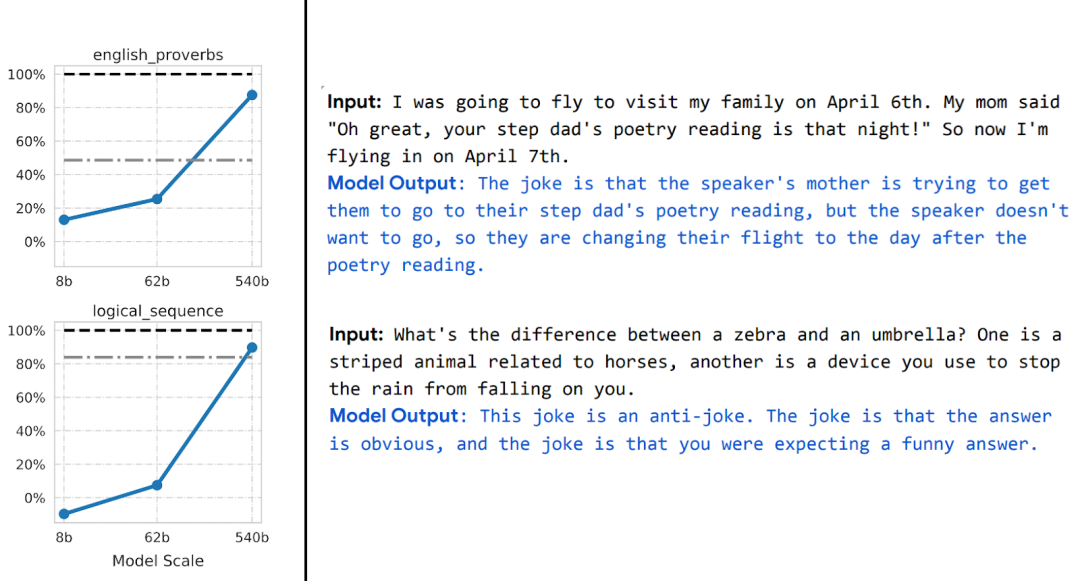
圖注：隨著模型大小的增加，PaLM 模型在一些基準測試中顯示出一些不連續的改進（上述圖中只有三個大小的警告），并解鎖了一些令人驚訝的功能，比如解釋笑話。

性能在很大程度上與損失或數據無關。不止一種自監督損失，有幾種對比性和重建性損失被用于圖像。語言模型有時采用單面重建（預測下一個標記），有時則是使用掩蔽模型，其目標是預測來自左右標記的掩蔽輸入。

也可以使用稍微不同的數據集，這可能會影響效率，但只要做出“合理”的選擇，常規情況下，原始資源比使用的特定損失或數據集更能預測性能。

有些實例比其他實例更難。這一點不只限于自監督學習，數據點或存在一些固有的“難度級別”。

事實上，有幾個實際證據表明，不同的學習算法有不同的“技能水平”，不同的點有不同的“難度水平”（分類器 f 對 x 進行正確分類的概率，隨著 f 的技能單向遞增，隨 x 的難度單向遞減）。“技能與難度”范式是對 Recht 和 Miller 等人所發現的“線上準確性”現象最清晰的解釋，在我同 Kaplun、Ghosh、Garg 和 Nakkiran 的合著論文中，還展示了數據集中的不同輸入如何具有固有的“難度特征”，常規情況下，該特征似乎對不同的模型來說是穩健的。

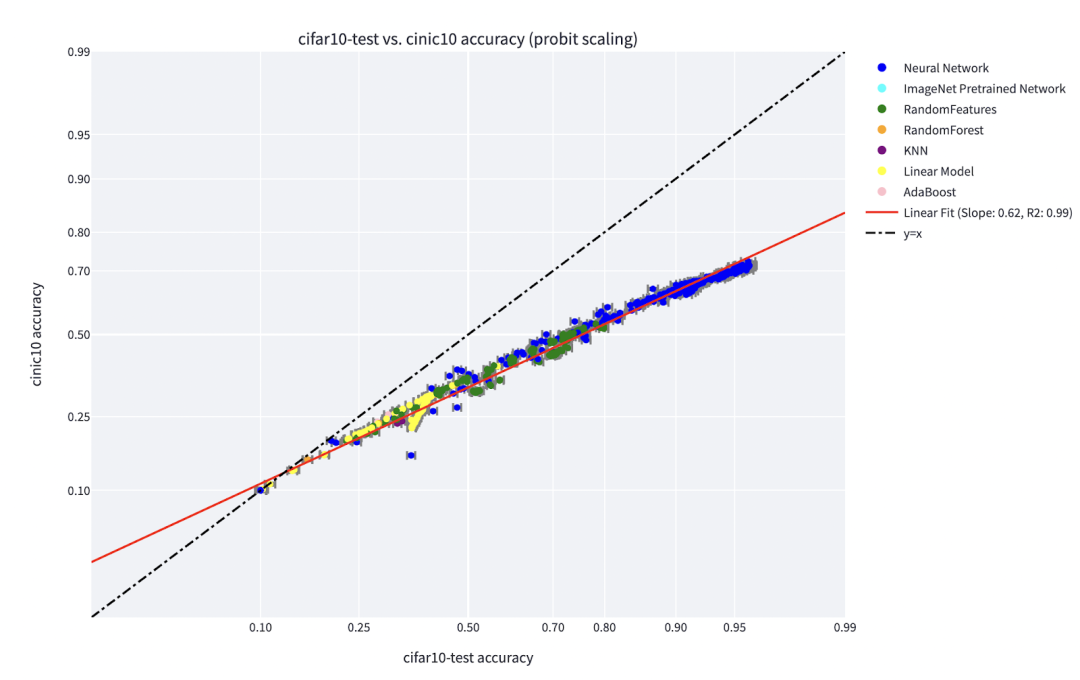
圖注：Miller 等人的圖表顯示了在 CIFAR-10 上訓練并在 CINIC-10 上測試的分類器的線現象準確性

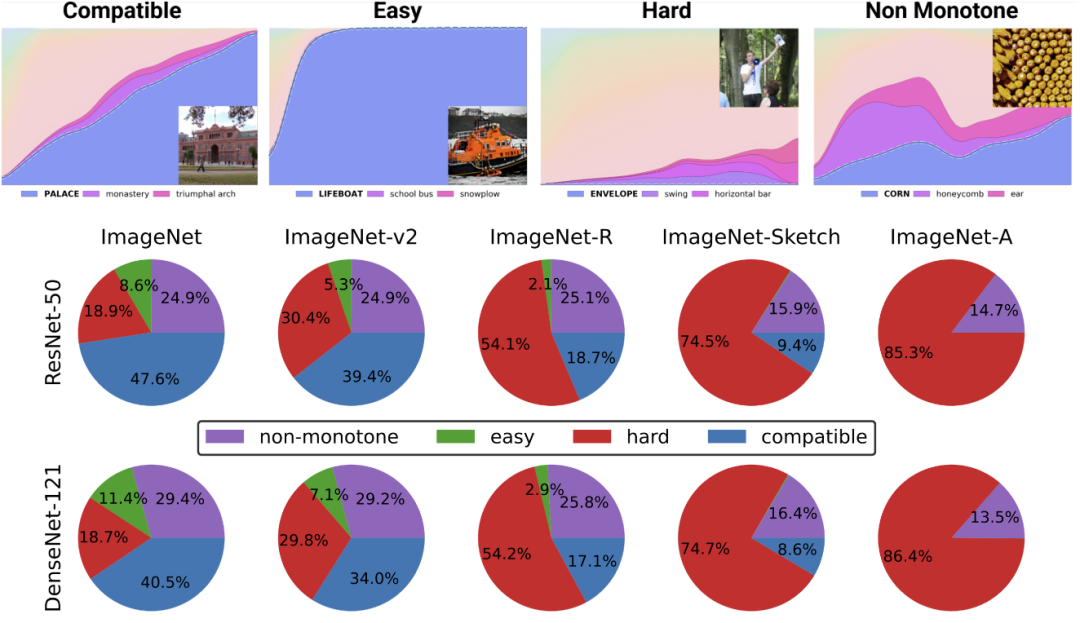
圖注：將數據集解構為來自 Kaplun 和 Ghosh 等人在論文“Deconstructing Distributions: A Pointwise Framework of Learning”中的不同“難度概況”點，以獲得越來越多的資源分類器。頂部圖表描述了最可能類的不同 softmax 概率，作為由訓練時間索引的某個類別分類器的全局精度的函數；底部餅圖展示了將不同數據集分解為不同類型的點。值得注意的是，這種分解對于不同的神經架構是相似的。

訓練即教學。現代對大模型的訓練似乎更像是在教學生，而不是讓模型適應數據，在學生不理解或看起來疲勞（訓練偏離）時采取“休息”或嘗試其他方式。Meta 大模型的訓練日志很有啟發性——除了硬件問題外，還可以看到一些干預措施，例如在訓練過程中切換不同的優化算法，甚至考慮“熱交換”激活函數（GELU 到 RELU）。如果將模型訓練視為擬合數據而不是學習表示，則后者沒有多大意義。

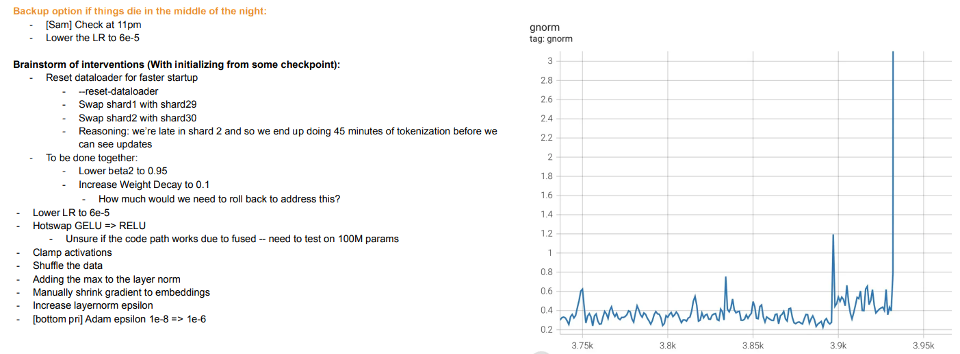
圖注：Meta 的訓練日志節選

下面探討兩種情況：

情況1：監督學習

到目前為止，我們只討論了自監督學習，但深度學習的典型例子仍然是監督學習，畢竟深度學習的 “ImageNet時刻”是來自ImageNet。那么，我們上面所探討的內容是否適用于監督學習呢？

首先，有監督的大規模深度學習的出現，在某種程度上是一個歷史性的意外，這得益于大型高質量標記數據集（即 ImageNet）的可用性。可以想象另一種歷史：深度學習首先通過無監督學習在自然語言處理方面取得突破性進展，然后才轉移到視覺和監督學習中。

其次，有一些證據表明，即使監督學習與自監督學習使用完全不同的損失函數，它們在“幕后”的行為也相似。兩者通常都能達到相同的性能。在“Revisiting Model Stitching to Compare Neural Representations”這篇論文中也發現，它們學習了相似的內部表示。具體來說，對于每一個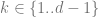，都可以將通過自監督訓練的深度 d 模型的首 k 層數與監督模型的最后 d-k 層數“縫合”起來，并且使性能幾乎保持原有水平。

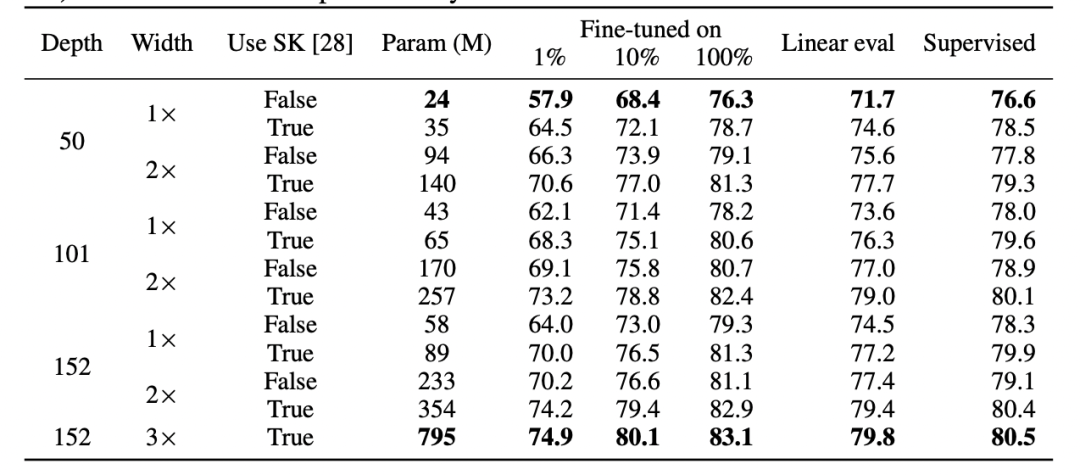
圖注：來自 Hinton 團隊論文“Big Self-Supervised Models are Strong Semi-Supervised Learners”的表格。請注意監督學習、微調 (100%) 自監督和自監督 + 線性探測在性能上的普遍相似性

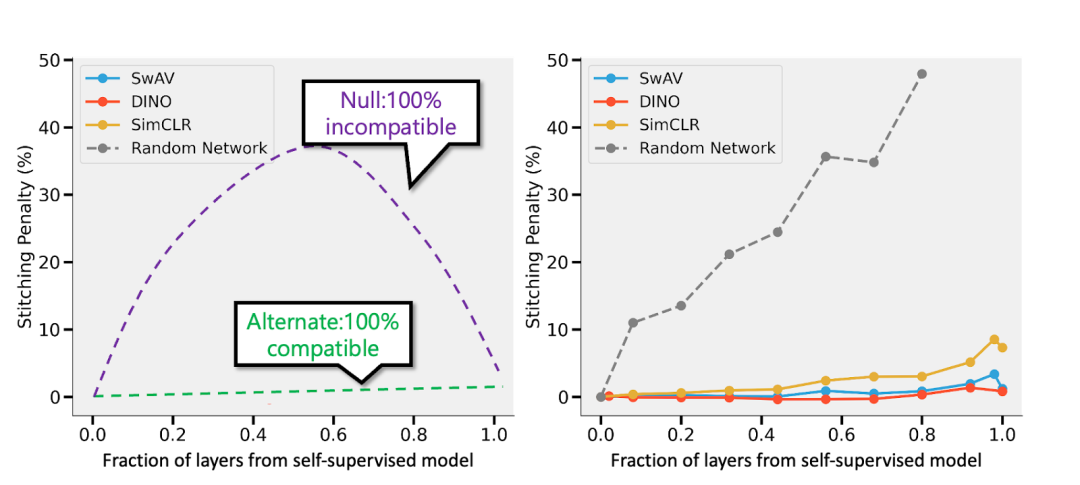
圖注：摘自論文“Revisiting Model Stitching to Compare Neural Representations”的自監督與監督模型。左圖——如果自監督模型的準確度比監督模型低3%，那么，完全兼容的表示將造成 p·3% 的拼接懲罰（p層來自自監督模型時）。如果模型完全不兼容，那么隨著更多模型的縫合，預計準確度會急劇下降。右圖——拼接不同自監督模型的實際結果。

自監督 + 簡單模型的優勢在于，它們可以將特征學習或“深度學習魔法”（深度表示函數的結果）與統計模型擬合（由線性或其他“簡單”分類器完成，分離出來在此表示之上）。

最后，雖然是推測，但“元學習”似乎通常等同于學習表示這一事實（詳情看論文“Rapid Learning or Feature Reuse? Towards Understanding the Effectiveness of MAML”），可以視為另一個支持本文觀點的證據，不管模型表面上優化的目標是什么。

情況2：過度參數化

讀者可能已經注意到，我跳過了統計學習模型與深度學習模型在實際應用中存在差異的典型例子，即缺少“偏差-方差權衡”以及過度參數化模型出色的泛化能力。

我不詳細講這些例子的原因有兩個：

一是如果監督學習確實等于自監督 + 簡單的“底層”學習，那么就可以解釋它的泛化能力（詳情請看論文“For self-supervised learning, Rationality implies generalization, provably”）；

二是我認為過度參數化并不是深度學習成功的關鍵。深度網絡之所以特別，并不是因為它們與樣本數量相比很大，而是因為它們的絕對值很大。實際上，無監督/自監督學習模型中通常沒有過度參數化。即使是大規模的語言模型，它們也只是數據集更大，但這也并沒有減少它們性能的神秘性。

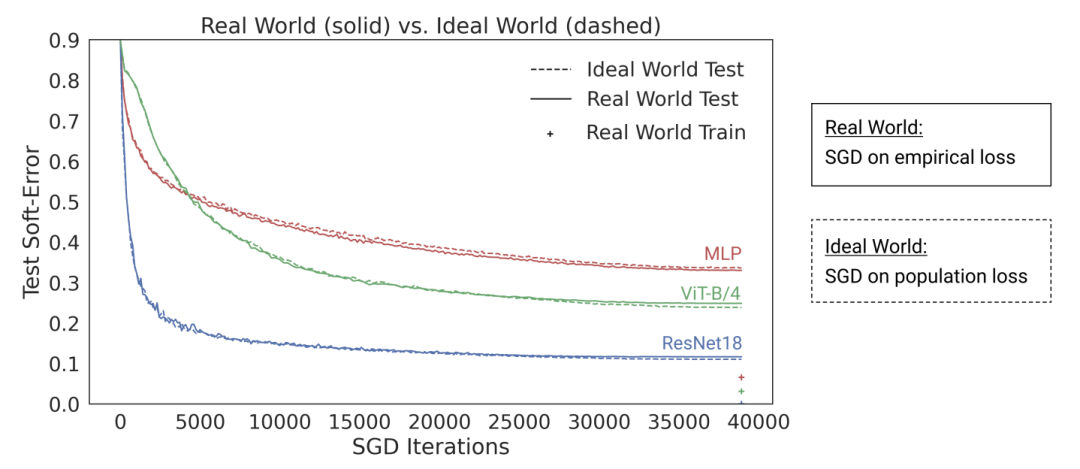
圖注：在“The Deep Bootstrap Framework: Good Online Learners are Good Offline Generalizers”這篇論文中，研究者的發現表明，如今的深度學習架構在“過度參數化”與“欠采樣”狀態下表現相似（其中，模型在有限數據上訓練多代，直到過度擬合：也就是上圖所示的“真實世界”），在“參數化不足”與“在線”情況下也如此（其中，模型只訓練一代，每個樣本只看到一次：也就是上圖中的“理想世界”）

毫無疑問，統計學習在深度學習中扮演著重要的角色。但是，如果僅僅將深度學習視為一個比經典模型擬合更多旋鈕（knobs）的模型，則會忽略其成功背后的許多因素。所謂的“人類學生”隱喻更是不恰當表述。

深度學習與生物進化相似，雖然對同一規則（即經驗損失的梯度下降）有許多重復的應用，但會產生高度復雜的結果。在不同的時間內，神經網絡的不同組成部分似乎會學習不同的內容，包括表示學習、預測擬合、隱式正則化和純噪聲等。目前我們仍在尋找正確的視角來提出有關深度學習的問題，更別說回答這些問題了。

任重道遠，與君共勉。

審核編輯 ：李倩