有符號數的計算在 Verilog中是一個很重要的問題（也很容易會被忽視），在使用 Verilog 語言編寫 FIR 濾波器時，需要涉及到有符號數的加法和乘法，在之前的程序中我把所有的輸入輸出和中間信號都定義成有符號數，這樣在計算時沒有出現問題（實際在之前的程序中遇到了問題，最后濾波結果不對，博客的程序是已經改正過的），下面實際試驗一下 Verilog 的乘法問題；

1.編寫程序測試無符號數和有符號數的乘法

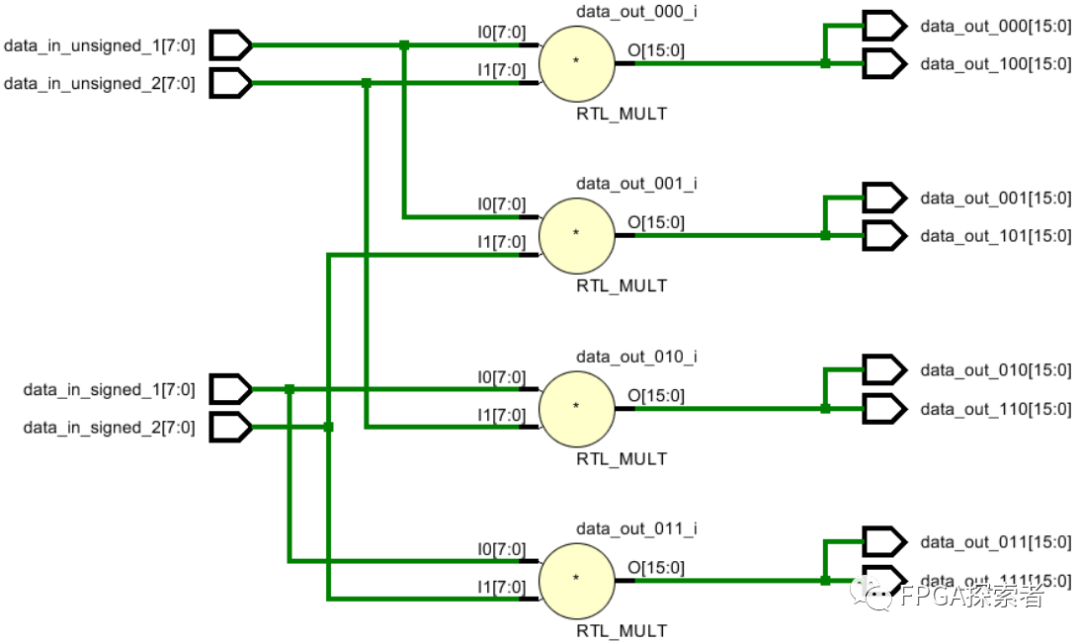
編寫程序如下，其中，乘法的兩個乘數分別是無符號、有符號的四種組合，輸出的積也是分為無符號和有符號，共計 8 種可能；

module signed_test(    input           [7:0]   data_in_unsigned_1,    input           [7:0]   data_in_unsigned_2,
    input   signed  [7:0]   data_in_signed_1,    input   signed  [7:0]   data_in_signed_2,
    output          [15:0]  data_out_000,    output          [15:0]  data_out_001,    output          [15:0]  data_out_010,    output          [15:0]  data_out_011,
    output  signed  [15:0]  data_out_100,    output  signed  [15:0]  data_out_101,    output  signed  [15:0]  data_out_110,    output  signed  [15:0]  data_out_111    );
//無符號 = 無符號 * 無符號assign data_out_000 = data_in_unsigned_1    * data_in_unsigned_2;//無符號 = 無符號 * 有符號assign data_out_001 = data_in_unsigned_1    * data_in_signed_2;//無符號 = 有符號 * 無符號assign data_out_010 = data_in_signed_1      * data_in_unsigned_2;//無符號 = 有符號 * 有符號assign data_out_011 = data_in_signed_1      * data_in_signed_2;
//有符號 = 無符號 * 無符號assign data_out_100 = data_in_unsigned_1    * data_in_unsigned_2;//有符號 = 無符號 * 有符號assign data_out_101 = data_in_unsigned_1    * data_in_signed_2;//有符號 = 有符號 * 無符號assign data_out_110 = data_in_signed_1      * data_in_unsigned_2;//有符號 = 有符號 * 有符號assign data_out_111 = data_in_signed_1      * data_in_signed_2;
endmodule

生成的 RTL 圖如下：

可以看到，輸出的積和符號無關，有符號數和無符號數實際上是同一個數，只看我們怎么定義它，比如乘積是 16 位的二進制 16’b1100_0000_0000_0011，當我們認為它是無符號數是，最高位的 1 就不是符號位，而是 2^15（2的15次方），這樣這個數代表的十進制是 2^15 + 2^14 + 2^1 + 2^0 = 49155；

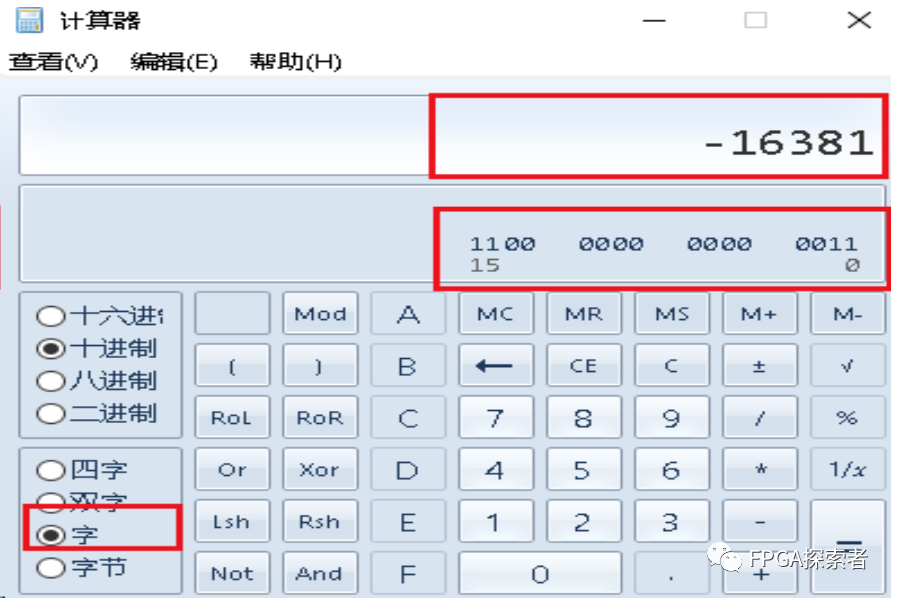
如果把 16 位的二進制 16’b1100_0000_0000_0011 當成是一個有符號數來看，那么最高位是符號位，且剩下的數據時原來的數據二進制表示后取反再加1（補碼表示），要計算它對應的十進制數

（1）先去掉符號位，保留剩下的 15-bit的 100_0000_0000_0011；

（2）把 100_0000_0000_0011 取反，得到 011_1111_1111_1100；

（3）把 011_1111_1111_1100 的最低位 + 1，得到 011_1111_1111_1101；

（4）011_1111_1111_1101 按照無符號數換算成十進制是 16381；

（5）把最高位符號位加上，0代表正數，1代表負數，所以最后換算是 -16831；

Windows計算器默認最高位是符號位；

測試數據如下：

initial begin        data_in_unsigned_1 = 8'hff;       //255data_in_unsigned_2=8'hf0;      //240data_in_signed_1=8'hff;  //-1data_in_signed_2=8'hf0;  //-16    #200;        data_in_unsigned_1 = 8'hff;       //255        data_in_unsigned_2 = 8'h0f;       //15        data_in_signed_1 = 8'hff;         //-1data_in_signed_2=8'h0f;  //15    #200;        data_in_unsigned_1 = 8'd127;      //127data_in_unsigned_2=8'd15;//15        data_in_signed_1 = -8'sd127;      //-127，十進制有符號數賦值，必須要用 sd 表示data_in_signed_2=-8'sd15;//-15    #200;             data_in_unsigned_1 = 8'd128;      //128        data_in_unsigned_2 = 8'd15;       //15               data_in_signed_1 = -8'sd128;      //-128data_in_signed_2=-8'sd15;//-15    #200;        data_in_unsigned_1 = 8'd127;       //127        data_in_unsigned_2 = 8'd15;        //15           data_in_signed_1=-8'sd127;  //-127data_in_signed_2=8'sd15;//15    #200;             data_in_unsigned_1 = 8'd128;       //128        data_in_unsigned_2 = 8'd15;        //15               data_in_signed_1=-8'sd128;  //-128data_in_signed_2=8'sd15;//15    #200;        data_in_unsigned_1 = 8'd127;       //127data_in_unsigned_2=8'd15;        //15        data_in_signed_1 = 8'sd127;        //127data_in_signed_2=-8'sd15;//-15    #200;                  data_in_unsigned_1 = 8'd127;       //127        data_in_unsigned_2 = 8'd15;        //15        data_in_signed_1 = 8'sd127;        //127data_in_signed_2=8'sd15;//15    #200;    $stop;end

2.仿真分析

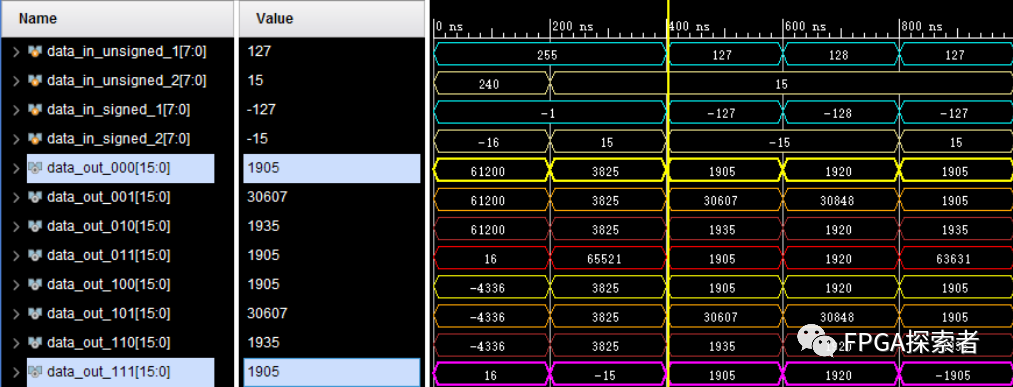
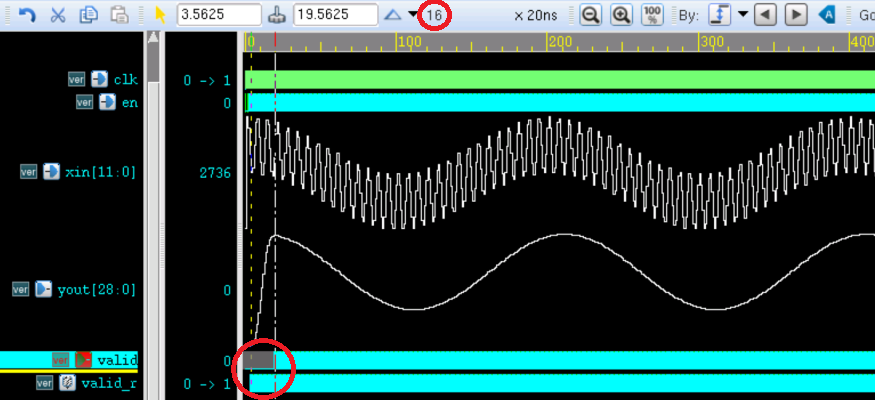
計算的結果仿真如下：

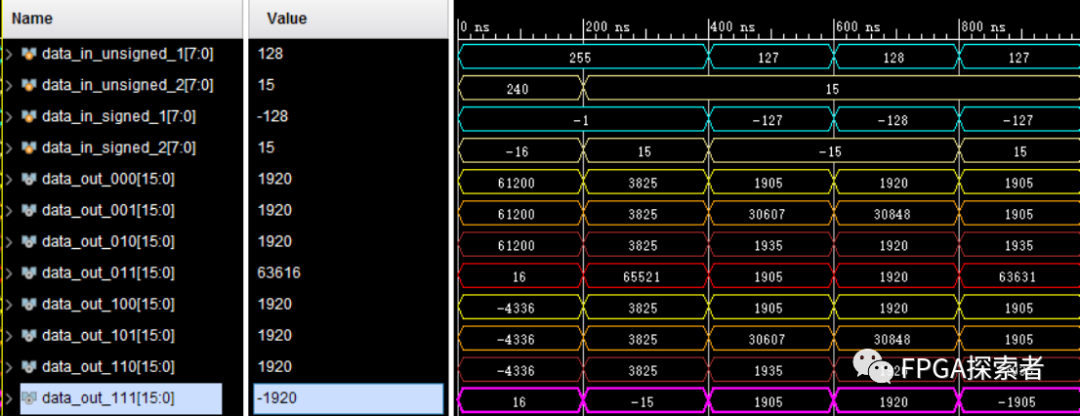
對上圖分析：

（1）在 0~400 ns，仿真中使用十六進制賦值相同的十六進制數據給乘數，讓乘數分別以無符號數和有符號數進行讀取，可以看到對 8’hff（對應二進制 8’b1111_1111）以無符號數讀取時是按照 原碼讀取，對應十進制 255，以有符號數讀取時是按照補碼讀取，按照上文所說的去掉符號位后取反、加1再計算十進制得 -1;

（2）直接賦值十進制數據，乘數在以無符號數讀取時時按照原碼讀取，127就對應 8 位二進制數 8’b0111_1111，十進制 128 就對應 8 位二進制 8’b1000_0000；而以有符號數讀取的時候是會直接轉換為補碼形式，如 -127，先去掉符號位是 127，對應 7 位二進制數 7’b111_1111，取反為 7’b000_0000，加 1 為 7’b000_0001，將符號位補回到最高位為 8’b1000_0001；對于 -128 的表示比較特殊，8-bit的二進制數最高位是符號位，表示正負，剩下的 7-bit 能夠表示的數的范圍是 0 ~ 127，前面加上 ±就能表示 -127 ~ 127，其中有 2 個數很特殊就是 8’b0000_0000 和 8’b1000_0000，按照上面會出現 +0 和 -0，為了區分出這兩個數，前人定義 8’b0000_0000 表示 0，而 8’b1000_0000 表示 -128，這樣不僅能區分開兩個數，還多表示了一個數 -128（整個計算機體系通用，其他位數時類似表示一個負數）；

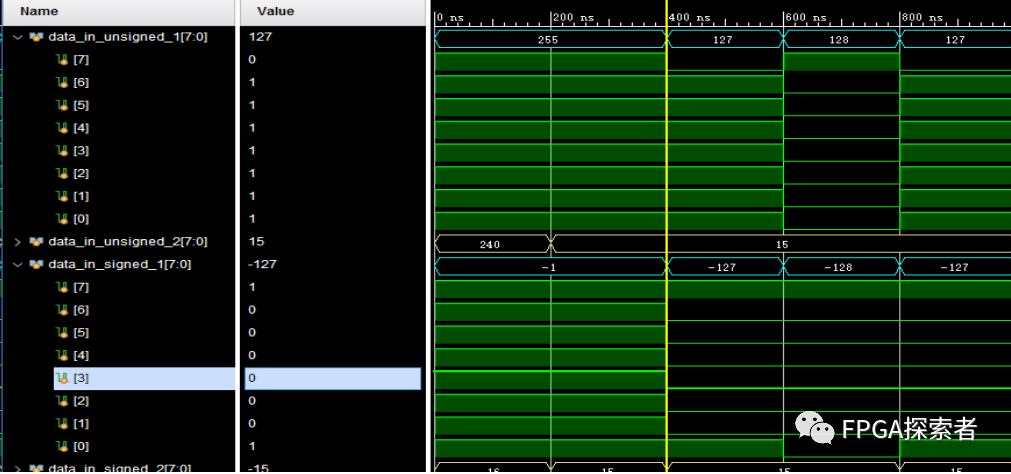
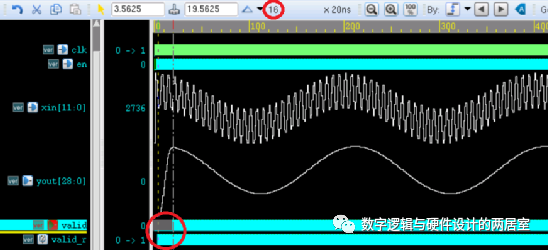
（3）實際上，觀察下圖數據可以發現，只有data_out_000 和 data_out_111 的數據時全部計算正確的，這也符合常理：

無符號 * 無符號 =無符號；

有符號 * 有符號 =有符號；

其它的計算為什么會出錯呢？實際上這里遵循一個原則：

如果表達式中有一個無符號數，則所有的操作數都會被強行轉換為無符號數；

這樣也就解釋了 0~400 ns時的 data_out_001 和 data_out_010 的計算結果和 data_out_000 完全一致，它們都是把賦值的 8 位十六進制數當做無符號數計算的（這里不存在十進制到二進制原碼、補碼換算的問題，因為給的是十六進制）；

當后面設計輸入輸出時，如果是有符號，那么將相關計算的輸入/輸出和中間量都顯式的用 signed定義；

3.有符號數乘法的另一種計算

前面說的計算時將涉及到的相關量全部定義為有符號數是一種計算方法，此外，通常情況下可能會定義的無符號數，但是實際傳入的是有符號數，比如下面的輸入和輸出都沒有指定成 signed有符號數，計算時默認是按照無符號數計算（實際上我感覺是把讀取到的 8 位二進制數當做原碼去算），此時若外部傳入的數據實際上是有符號數（比如 FIR 濾波器傳入了正負均有的待濾波信號），那么需要對符號位進行擴展來計算乘法和加法；

module signed_test_2(    input   [7:0]   data_in_1,    input   [7:0]   data_in_2,    output  [15:0]  data_out_1,    output  [15:0]  data_out_2);

對于乘法，需要擴展符號位 到 和積的位數相等，比如乘數a為 N-bit，乘數 b 為M-bit，兩個相乘得到 N+M 位數據，此時需要對 a擴展 M-bit到 N+M 位，對 b擴展 N-bit到 N+M 位；

下面，使用位拼接符 {}來做演示，位拼接符可以按照二進制的位來進行高低位的拼接，假設 data_in_1=8’b1000_0011，對于 {{8{data_in_1[7]}},data_in_1} 可以這樣理解：

（1）先看 8{data_in_1[7]}，表示取出 8-bit數據 data_in_1 的最高位 data_in_1[7]，重復 8 次，相當于 { data_in_1[7], data_in_1[7], data_in_1[7], data_in_1[7], data_in_1[7], data_in_1[7], data_in_1[7], data_in_1[7] }，即高位擴展 8-bit的 1

（2）{{8{data_in_1[7]}},data_in_1} 相當于在 data_in_1 的前面補上 8 個 data_in_1[7]，即 結果為 16-bit 的 16’b1111_1111_1000_0011；

//不做符號位擴展，直接相乘assign data_out_1 = data_in_1 * data_in_2;//做符號位擴展，再相乘assign data_out_2 = {{8{data_in_1[7]}},data_in_1} * {{8{data_in_2[7]}},data_in_2};

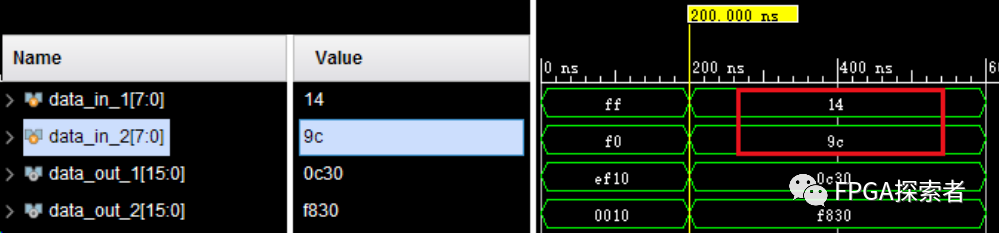
仿真測試數據如下，1處用十六進制給出數據，2處用有符號的十進制賦值，3處是為了和 2處對比，看最后賦值是否一樣（看到有博客說 3 的賦值是錯的，所以測試一下）；

仿真結果如下，可以看到上圖 2 處和 3 處的賦值在仿真時是同樣的數據，把所有數據都用有符號的十進制數顯示（右鍵數據 Radix-> Signed Decimal）；

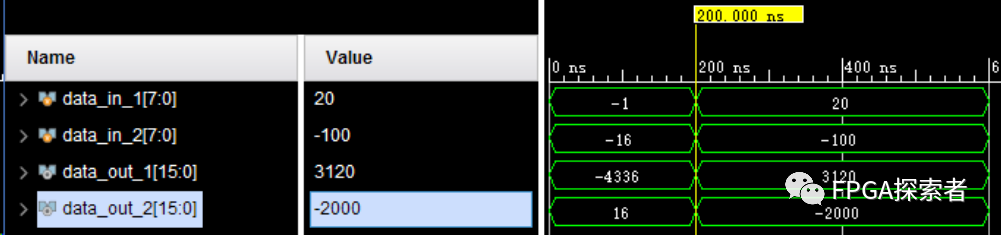
可以看到，data_out_1的結果是錯的（沒有補符號位），data_out_2的結果是對的（補符號位）；

對有符號數的加法，同樣的，要么相關的運算全部定義成有符號數，要么進行符號位的擴展，對于加法操作，只需要每個被加數擴展 1 位符號位即可；

除此之外，還可以調用乘法器的 IP 來代替 乘法符號 *，或者加法器的 IP 來代替 加法符號 +，在 IP 核中配置輸入輸出為有符號數即可。