一、紅黑樹的底層邏輯
大家都聽說過紅黑樹,也都知道紅黑樹很厲害,是計算機里面評價非常高的數據結構。但是每當想學習紅黑樹的時候,卻總是找不到通俗易懂很好理解的學習資料。很多書上上來就是紅黑樹的定義,然后就是紅黑樹的實現,直接就把人給整暈了。光看紅黑樹的定義就有5條,為什么要有5條定義,為什么要這么定義,這么定義是什么意思,光定義都讓人懵了,更別說實現了。我看最近抖音上有很多人在講底層邏輯,只要你掌握了底層邏輯,其它的問題都不在話下,今天我們也來講一講紅黑樹的底層邏輯。
在講之前我們先介紹一下紅黑樹的誕生,紅黑樹是Rudolf Bayer在1972年首先提出來的,不過當時并不叫紅黑樹,而是叫對稱二叉 B 樹(symmetric binary B-trees)。后來在1978年Leo J. Guibas 和 Robert Sedgewick 對此數據結構進行了修改和完善,并重新命名為紅黑樹。為什么叫紅黑樹呢?有兩種說法,因為紅黑樹中要對節(jié)點連接做兩種顏色的區(qū)分,一說是因為當時的書寫筆只有紅色和黑色兩種顏色,另一說是當時的打印機只有紅和黑兩種顏色。
1.1 紅黑樹的本質
什么是紅黑樹,紅黑樹的本質是什么?一句話就可以說清楚,紅黑樹是二叉樹的身體、2-3 B樹的靈魂,用計算機的語言來說就是,紅黑樹是二叉樹的存儲結構、2-3 B樹的操作邏輯。那么紅黑樹為什么是這樣的呢?這就和遺傳學中的道理是一樣的了,是為了取得雜交優(yōu)勢,既繼承父本的優(yōu)勢又繼承母本的優(yōu)勢,同時又拋棄了父本和母本的劣勢。我們把二叉樹看成是母本,2-3 B樹看成是父本,母本的優(yōu)勢就是存儲結構簡單,還有比二叉樹更簡單的樹形結構嗎,沒有了。父本的優(yōu)勢就是B樹是絕對平衡樹,任何時候都是絕對平衡的。但是父本的劣勢也是因于此,為了實現絕對平衡,B樹的存儲結構比較復雜,當然操作邏輯也比較復雜。而二叉樹雖然存儲結構簡單,操作也簡單,但是它最大的缺點就是不一定平衡,一棵樹如果不平衡,它的操作復雜度就會從O(logn)退化為O(n),這是一個很嚴重的問題。為了實現一個既平衡又相對簡單的樹形結構,于是有人就想到了把二叉樹和2-3 B樹給結合起來,取二叉樹的存儲結構和2-3 B樹的操作邏輯,用二叉樹來模擬2-3 B樹,于是紅黑樹就誕生了,這樣紅黑樹就既實現了存儲結構簡單又實現了平衡的效果。紅黑樹的定義也就比較好理解了,就是為了保證紅黑樹在邏輯上是一顆2-3 B 樹。我們這里暫時先不講紅黑樹的定義,我們先來講一講2-3 B樹,當你把B樹的邏輯理解透了,那么掌握紅黑樹的定義和實現就易如反掌。這里說的二叉樹具體來說是二叉搜索樹,下文也會簡單地講一下。
1.2 B樹簡介
樹形結構首先可以分為等叉樹和不等叉樹,等叉樹是每個節(jié)點的鍵值個數都相同、子節(jié)點個數也都相同,不等叉樹是每個節(jié)點的鍵值個數不一定相同、子節(jié)點個數也不一定相同。
最簡單的等叉樹是二叉樹,直接二叉樹的作用并不大,我們一般會要求二叉樹所有的節(jié)點按照一定的順序排列,這樣我們進行插入、刪除、查找時效率就會非常高,我們把這樣的樹叫做二叉搜索樹或者二叉查找樹。它的具體定義是這樣的,二叉搜索樹,要么是個空樹,要么符合以下幾個條件,1.左子樹如果存在的話,左子樹所有節(jié)點的鍵值都要小于根節(jié)點的鍵值,2.右子樹如果存在的話,右子樹所有節(jié)點的鍵值都要大于根節(jié)點的鍵值,3.它的所有子樹也都要符合前面的兩個條件(前面的小于同時換成大于也成立)。經過這樣定義之后,二叉樹就變成了二叉搜索樹,它的插入、刪除、查找效率一般情況下都是O(logn)。等叉樹還有三叉樹、四叉樹、五叉樹等,但是它們和二叉樹相比,除了更復雜以外,好像也沒有啥優(yōu)點,所以很少聽到有人用過。
不等叉樹和等叉樹相比除了更省空間以外,好像也沒啥特別的用處,但是如果我們對不等叉樹的節(jié)點鍵值數和插入、刪除邏輯添加一些特殊的要求,使其能達到絕對平衡的效果,我們就把這種樹叫做B樹。B樹全稱Balance Tree,是一種自平衡樹。它和等叉樹最大的不同首先表現在存儲結構上,等叉樹上每個節(jié)點的鍵值數和分叉數都是相同的,而B樹則不是。如果某個B樹上所有節(jié)點的分叉數最大值是m,則把這個B數叫做m階B樹。下面我們來看一下B樹的具體定義:
所有節(jié)點最多有m個子節(jié)點。
非根非葉子節(jié)點至少有m/2(向上取整)個子節(jié)點。
根節(jié)點至少有兩個子節(jié)點(除非總結點數都不夠3個)。
所有葉子節(jié)點都在同一層。
任意節(jié)點如果有k個鍵值,則有k+1個子節(jié)點指針,鍵值要按照從小到大排列,子節(jié)點樹上所有的鍵值都要在對應的兩個鍵值之間。
B樹的定義好像很復雜,但是仔細分析一下也不復雜,可以分為3類。一是對子節(jié)點的個數進行限制,包括1、2、3三條,1是限制最大子節(jié)點數的,這也是m階B樹的m的由來,2是限制非根非葉子節(jié)點的子節(jié)點數,葉子節(jié)點的子節(jié)點數是0,所以才叫葉子,沒啥限制的,根比較特殊,下一條說,普通節(jié)點的子節(jié)點數至少要是m/2(向上取整)個,這么要求是為了提高樹的緊湊性,避免樹變得過于瘦高,3是限制根節(jié)點的子節(jié)點個數,要求根節(jié)點至少有2個子節(jié)點。二是要求整個樹是要有序的,是5,第5條雖然不好用語言描述,但是它的意思是很簡單明確的,就是鍵值要從小到大排序,鍵值之間的子節(jié)點的值也要在兩個鍵值之間,如果是兩端的,則要小于最小鍵值,或者大于最大鍵值。三是對樹高的要求,是4,第4條說的是所有葉子都在同一層,也就是說每一個葉子的深度都是相同的,這也是整個樹的高度,這一條直接規(guī)定了B樹是一個絕對平衡樹,不會出現退化成線性結構的可能,所以B樹的效率一直是O(logn)的,沒有例外情況。
B樹的5條定義,其它的都好實現,就第4條比較難,而它也是B樹保持絕對平衡的關鍵。那么第4條如何實現呢?這就要對它的插入和刪除做特殊規(guī)定了。插入的時候只能在葉子節(jié)點進行插入,如果插入后葉子節(jié)點滿了,則會對這個葉子節(jié)點進行分裂操作,選取中間鍵值把這個葉子一分為三,小于這個鍵值的重新組成一個節(jié)點,大于這個鍵值的重新組成一個節(jié)點,然后把這個中間鍵值送給父節(jié)點。如果父節(jié)點沒有滿,則插入操作結束。如果父節(jié)點也滿了,則遞歸此操作,直至根節(jié)點。如果根節(jié)點也滿了,則對根節(jié)點進行分裂,生成新的根節(jié)點,這時樹的高度就會增加1,由于是在根部增長,所以所有節(jié)點的高度都增加了,整個樹還是平衡的。總結起來,B樹插入的特點就是底部插入、根部增長,而二叉樹是底部插入、底部增長,時間長了容易生長不平衡,B樹則沒有這種煩惱,它一直都是平衡的。雖然B樹的插入一直是平衡的,但是如果刪除操作是直接執(zhí)行的,也會導致B樹被刪的不平衡了,所以B樹的刪除也要特殊操作才行。B樹的刪除更加復雜,我們首先考慮如果被刪除的鍵值不在葉子節(jié)點上,我們找到它的后繼,它的后繼一定是在葉子節(jié)點上,然后用后繼覆蓋它,再去刪除這個后繼,然后就是葉子節(jié)點的刪除了。如果葉子節(jié)點里面的鍵值個數足夠,刪除一個也滿足B樹要求的個數,則直接刪除,沒有問題。如果自己的鍵值數不夠了,則要考慮向臨近的兄弟節(jié)點借,借的時候要經過父節(jié)點轉手一次,并不是直接借人家的節(jié)點值,而是兄弟節(jié)點給父節(jié)點一個合適的鍵值,父節(jié)點再拿一個合適的鍵值給自己。如果兄弟節(jié)點也沒有多余的鍵值可以借了,那就要向父節(jié)點借一個元素并和兄弟節(jié)點進行合并處理,自己和左兄弟節(jié)點或者右兄弟節(jié)點再加上父節(jié)點的一個鍵值,合并成一個新的節(jié)點。如果父節(jié)點被借走了一個鍵值之后,鍵值數也小于要求了,則繼續(xù)此過程,直至最后向根節(jié)點借,如果根節(jié)點也被借沒了,則新合并的節(jié)點成為根節(jié)點,B樹的高度減1。
我們對B樹有了基本的了解,對B樹的插入刪除操作也有了大概的認識,但是可能還不是很清晰,下一章我們以2-3 B樹為例,詳細地講一講B樹的操作邏輯。
二、2-3 B樹的操作邏輯
2-3 B樹是最簡單的B樹,它就是3階B樹,由于它的子節(jié)點個數是2或者3,所以大家都叫它2-3 B樹。同理,4階B樹也被大家廣泛的叫做2-3-4 B樹,2-3-4 B樹和2-3 B樹差別并不大,因為一個4節(jié)點可以很輕松的轉化為2個2節(jié)點,所以本文中就用2-3 B樹的邏輯來實現紅黑樹,不再討論2-3-4 B樹的情況了。
2-3 B樹就是3階B樹,我們把m階B樹的定義,把m=3代入進來看一下:
所有節(jié)點最多有3個子節(jié)點。
非根非葉子節(jié)點至少有3/2(向上取整)= 2個子節(jié)點。
根節(jié)點至少有兩個子節(jié)點(除非總結點數都不夠3個)。
所有葉子節(jié)點都在同一層。
任意節(jié)點有k(1或者2)個鍵值,則有k+1個子節(jié)點指針,鍵值要按照從小到大排列,子節(jié)點樹上所有的鍵值都要在對應的兩個鍵值之間。
這個定義和B樹的定義差別并不大,也沒有多少簡化,只不過是值具體化了而已。從這個定義中我們可以看出,2-3 B樹中一共有兩個類型的節(jié)點,2節(jié)點(單元素節(jié)點),3節(jié)點(雙元素節(jié)點),后面為了敘述方便我們可能會混用這兩對術語,后文也會混用元素和鍵值這對詞。我們先來看一個具體的2-3 B樹,先有個大概的認識。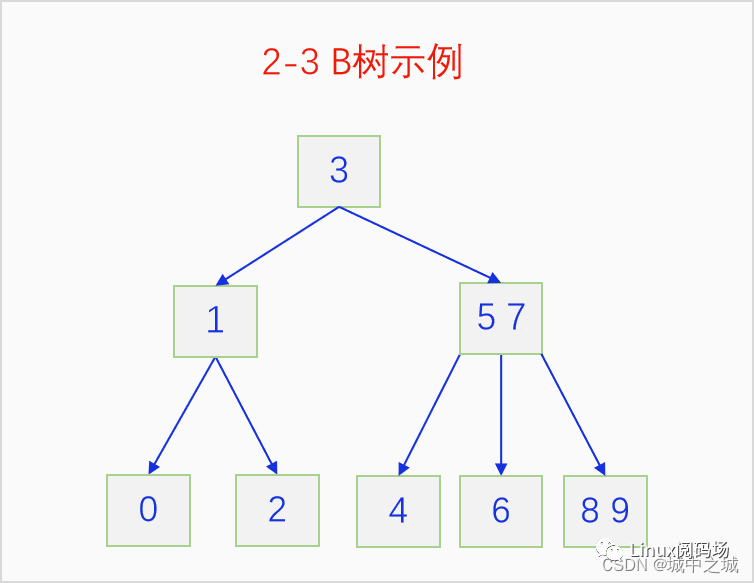
這是一個由0-9依次插入而形成的2-3 B樹,圖中的節(jié)點都是2節(jié)點和3節(jié)點,所有葉子節(jié)點都在最底層,高度是一樣的,3的左子樹都小于3,右子樹都大于3,對于節(jié)點57來說,4小于5, 6大于5小于7, 8、9都大于7,符合B樹的定義,B樹的第5條定義雖然不好描述的,但是看圖的話還是比較好理解的。但是B樹的插入和刪除操作是不太好理解的,下面我們用兩節(jié)時間來詳細講一講。
2.1 2-3 B樹的插入操作
B樹的插入并不是直接創(chuàng)建新節(jié)點,而是尋找在合適位置的葉子節(jié)點中插入元素,把自己的鍵值加入到這個葉子節(jié)點中去,如果這個葉子節(jié)點原本就只有一個元素,那么插入之后正好兩個元素,符合2-3 B樹的要求,插入完成。如果這個葉子節(jié)點已經有兩個元素了,插入后就有三個元素,那么就把中間的元素送給父節(jié)點,自己分裂成兩個節(jié)點。再看父節(jié)點,如果接收之后父節(jié)點也變成了3元素節(jié)點,那么就重復這個過程,直到根節(jié)點。如果此時根節(jié)點也是3元素節(jié)點,那么就把中間的鍵值拿出來創(chuàng)建新節(jié)點并成為新的根節(jié)點,原來的根節(jié)點分裂成兩個節(jié)點掛在新的根節(jié)點上,整個2-3 B樹的高度就增加了1。語言描述不太好懂的,下面我們用畫圖的方式詳細講一下把0-9依次插入一顆2-3 B樹的過程。
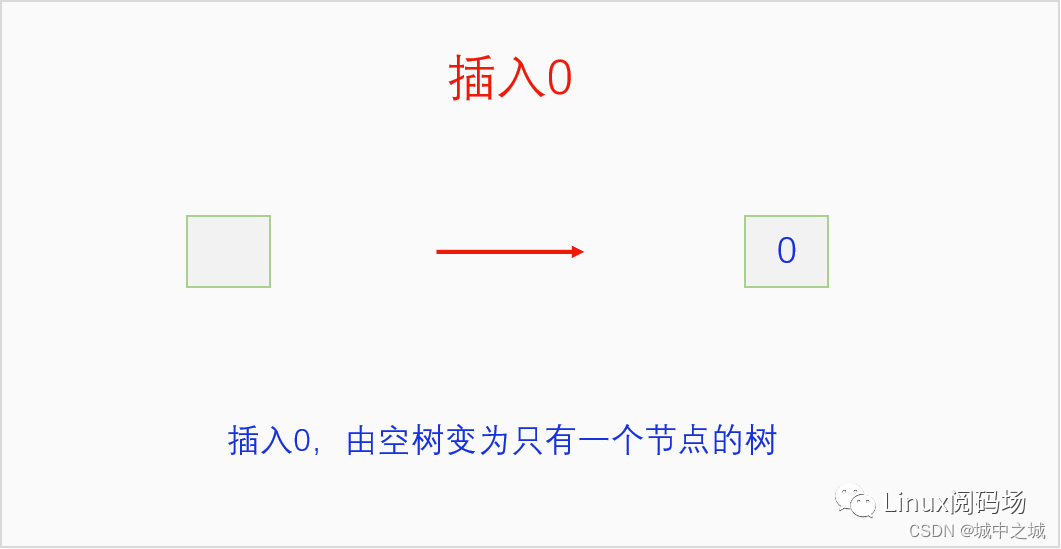

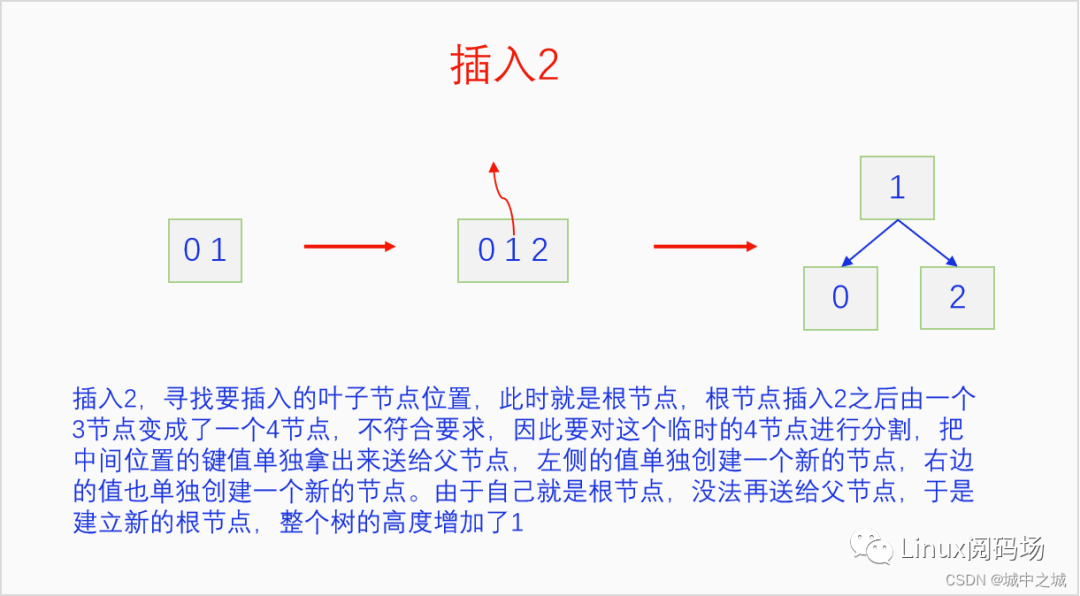
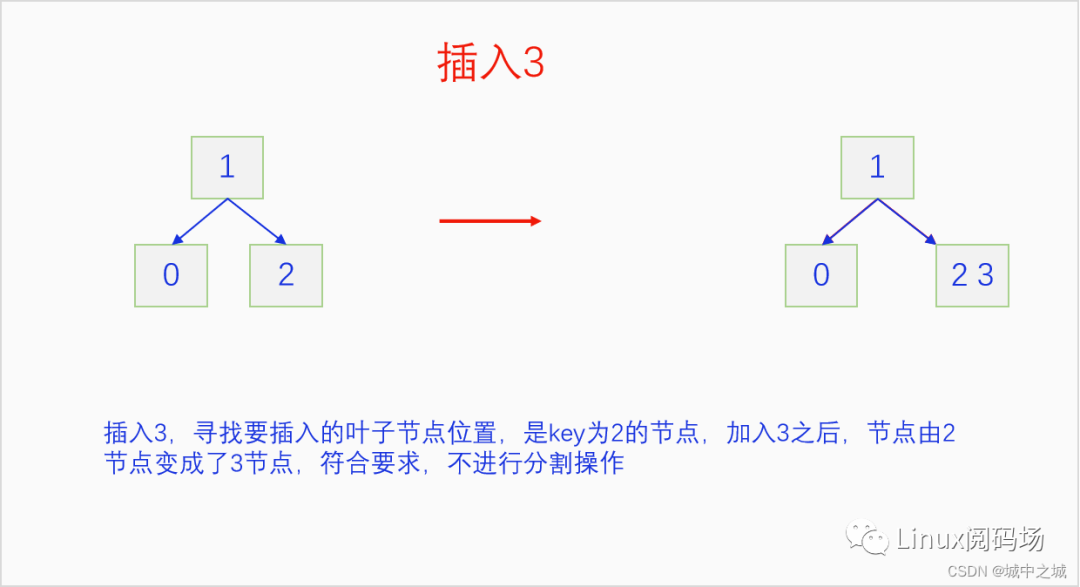
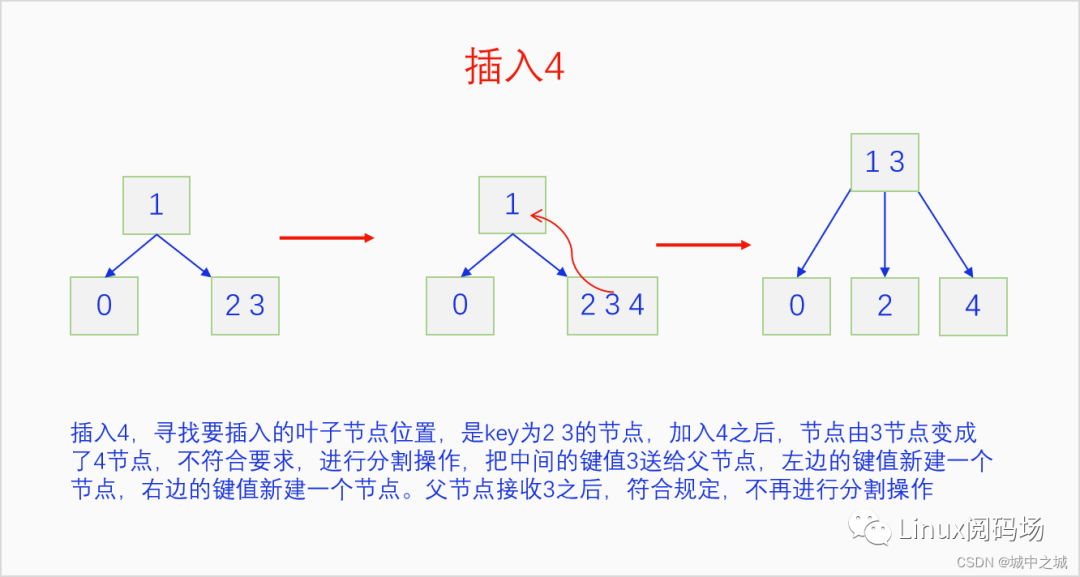
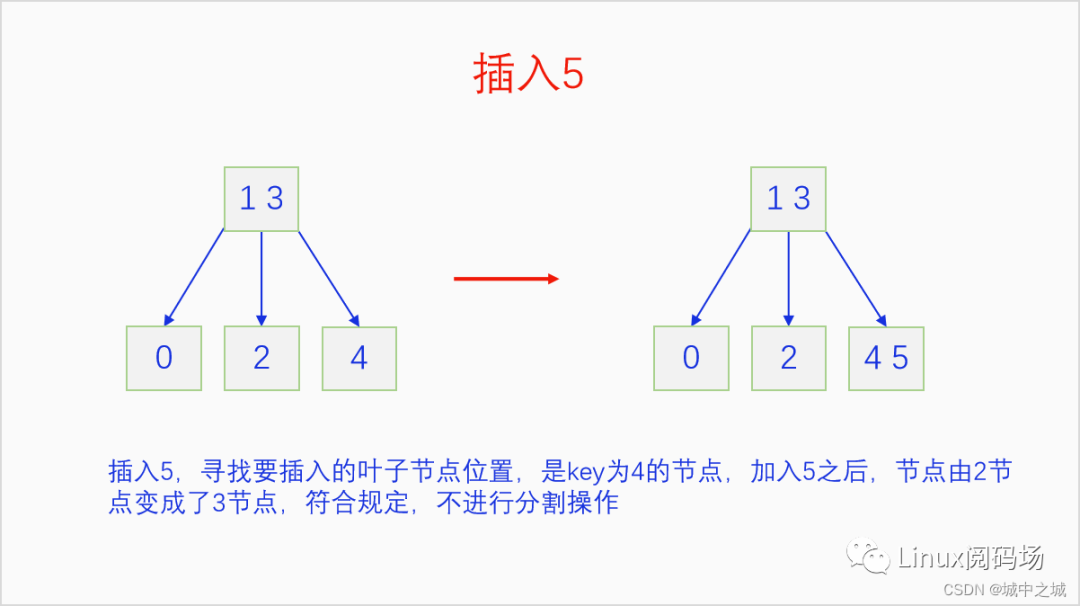

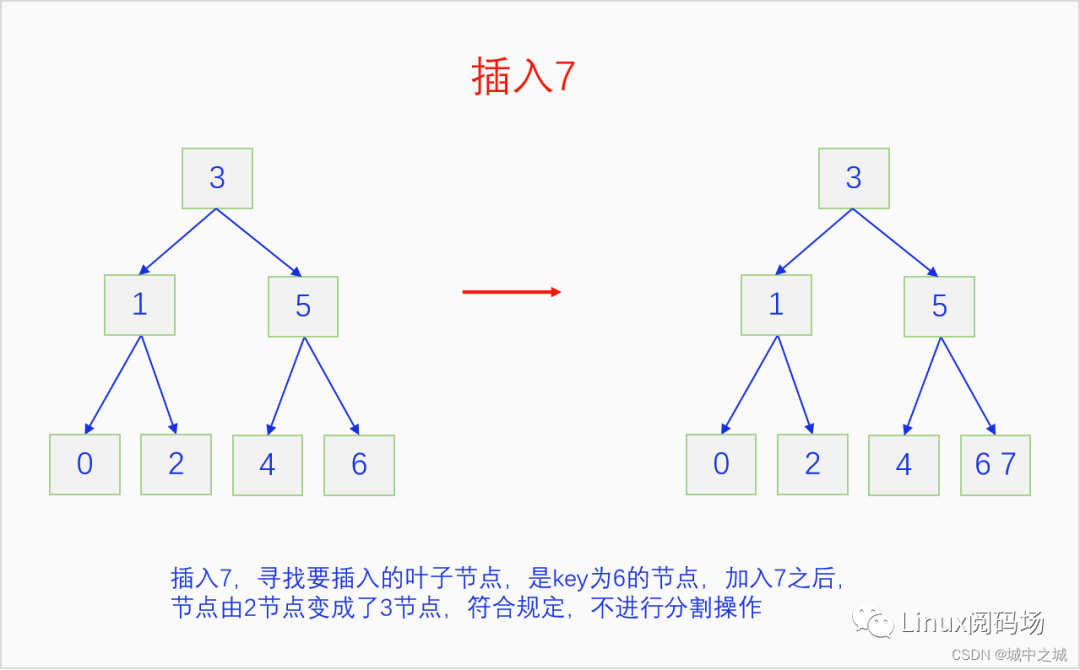
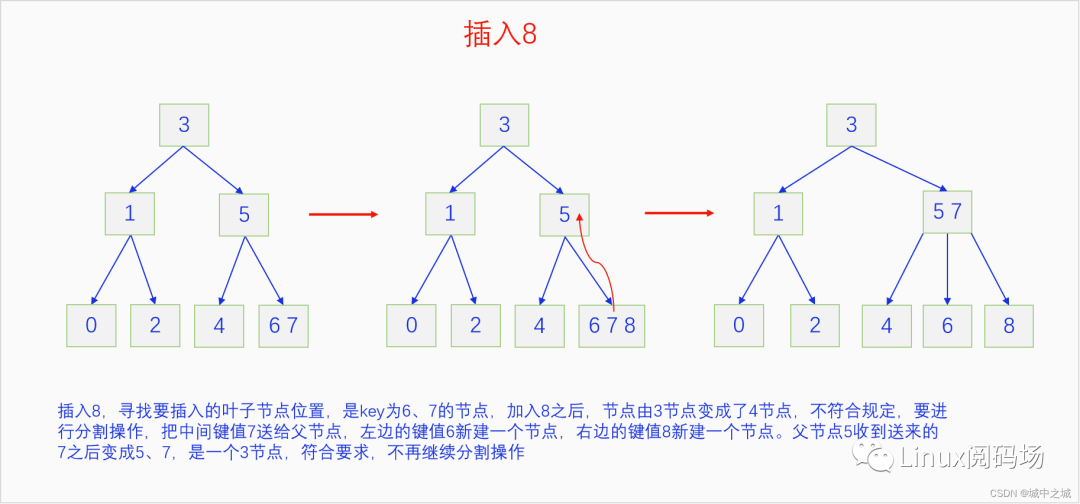
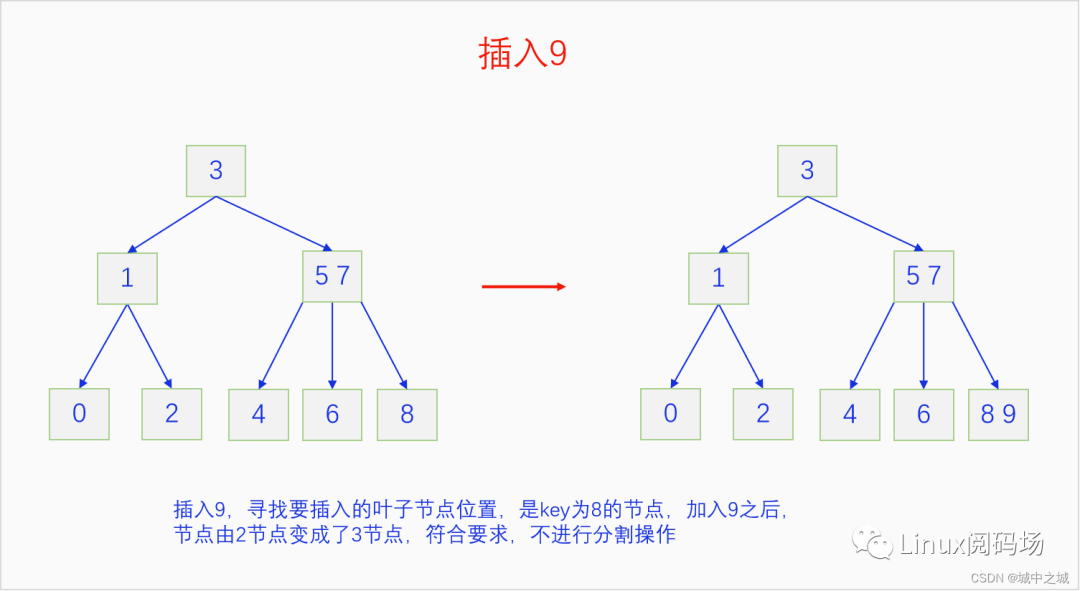
整個2-3 B樹的插入過程還是很
簡單的,都是在尋找到自己對應位置的節(jié)點,如果那個節(jié)點本來只有一個元素,再加入一個元素也沒有問題,過程就就結束了。如果那個節(jié)點本來有2個元素就麻煩了,3個元素擠在一起實在是太擠了,待不下,于是就把中間的元素送給父節(jié)點,自己這個節(jié)點分成兩個節(jié)點,左元素和右元素各占一個節(jié)點,新建立的兩個節(jié)點連接到父節(jié)點上。如果父節(jié)點此時也變成了3個元素,那就繼續(xù)這一過程,直到根節(jié)點。如果到根節(jié)點還是3個元素的話,把中間的鍵值單獨建立節(jié)點,成為新的根節(jié)點,原來的根節(jié)點一分為二,分別連接到新的根節(jié)點上,這個新建立的中間節(jié)點成為新的根節(jié)點。
2.2 2-3 B樹的刪除操作
B樹的刪除邏輯是比較復雜的,首先要考慮的是刪除的是不是葉子節(jié)點,如果不是葉子節(jié)點的話,先把它轉化成葉子節(jié)點,轉化的方式是找到它的后繼元素,然后把后繼元素的值復制給自己,然后把它的后繼元素給刪了。這里面有兩個問題,為什么這么操作是對的,怎么尋找后繼元素。這個留在本節(jié)的最后來回答。如果是葉子節(jié)點的話,那刪除就相對簡單了,如果這個葉子節(jié)點是雙元素節(jié)點的話,那就更簡單了,直接把元素刪除了就行了,不會破壞2-3 B樹的任何性質。如果葉子節(jié)點是單元素節(jié)點的話,就比較復雜了,直接刪除的話就違背了2-3 B樹的性質了。為此我們需要先借一個元素過來,要在不破壞2-3 B樹的性質的情況下借,借到之后我們就變成了一個雙元素節(jié)點了,就可以直接刪除元素了。借的話也分幾種情況,先給相鄰的兄弟節(jié)點借,如果兄弟節(jié)點有兩個元素的話就可以借,借的方式不是直接拿過來,而是把被借的元素給父節(jié)點,父節(jié)點再把另一個元素借給自己,被借和借到的元素不是同一個,這么做的目的是為了保持2-3 B樹整體上仍然是有序樹。如果從相鄰的兄弟節(jié)點借不到,那就從父節(jié)點借,如果父節(jié)點有兩個元素的話就可以直接借,借來之后并不是直接加入到自己的節(jié)點中,而是自己和借來的元素和一個相鄰的兄弟節(jié)點合并成一個新節(jié)點,這么做是因為父節(jié)點少了一個元素就少了一個子指針,所以得合并子節(jié)點才行。如果父節(jié)點是也是單元素節(jié)點的話怎么辦呢,沒有辦法,強行把父節(jié)點的一個元素借過來,這時父節(jié)點空了,它就需要繼續(xù)借,如果能從它的兄弟節(jié)點或者父節(jié)點借來就沒事了,如果也借不來的話,就再強行向父節(jié)點的父節(jié)點借,一直持續(xù)這個過程,直到根節(jié)點。如果根節(jié)點也被借空了,那么整個2-3 B樹的高度就會減少1。
我們同樣以畫圖的方式把2-3 B樹的刪除過程給演示一遍。
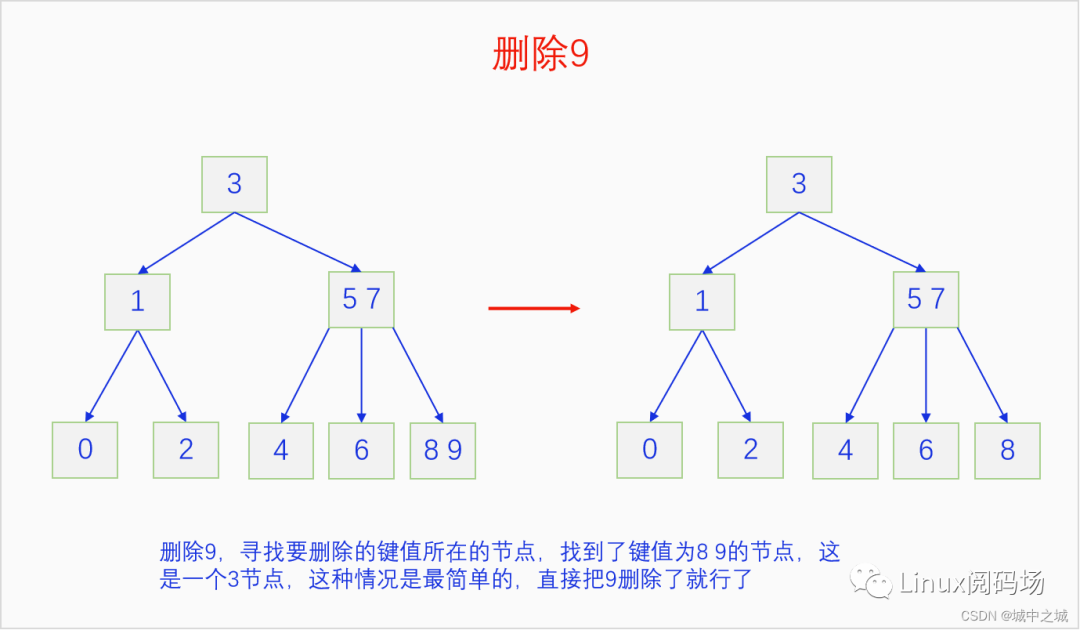
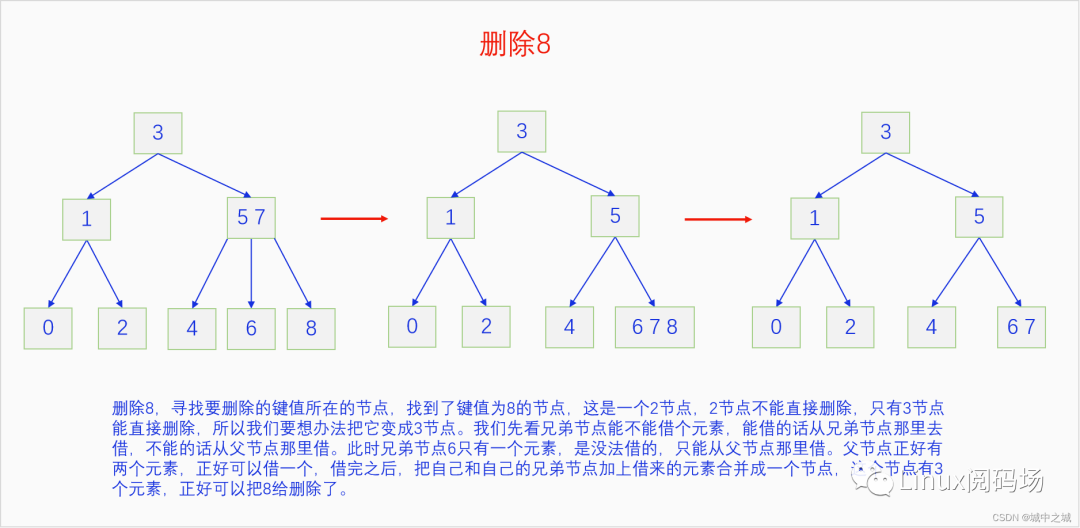
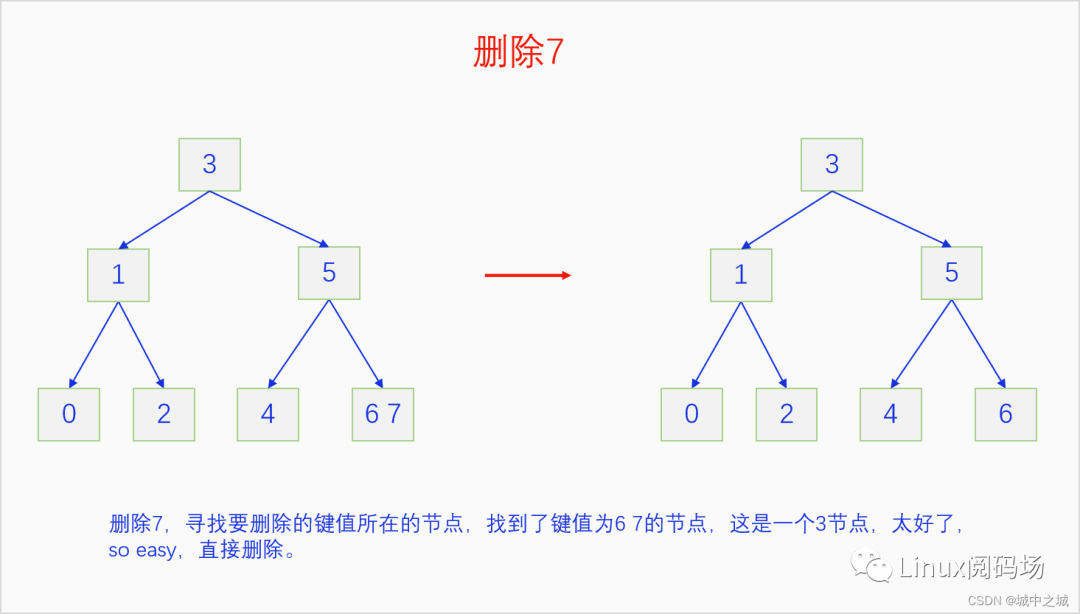
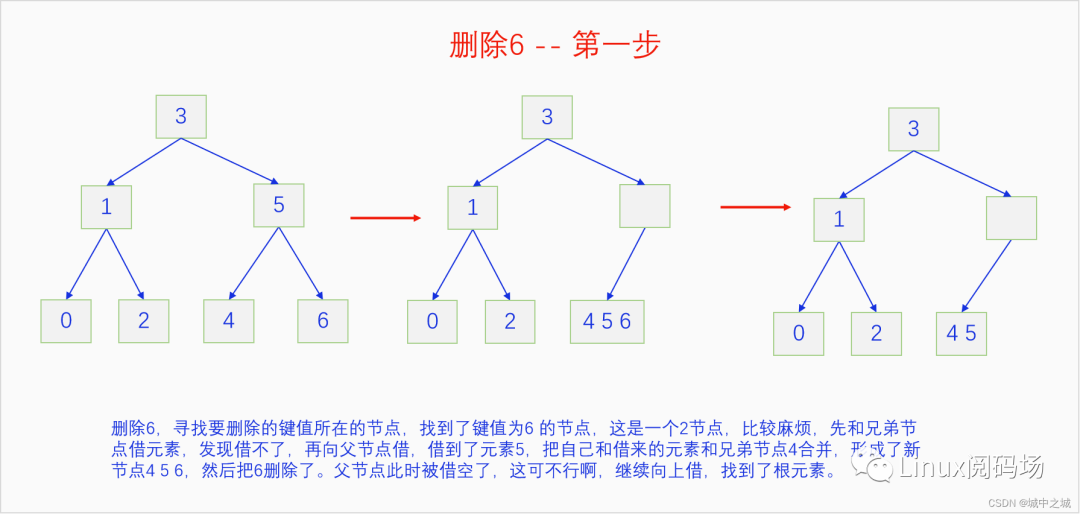
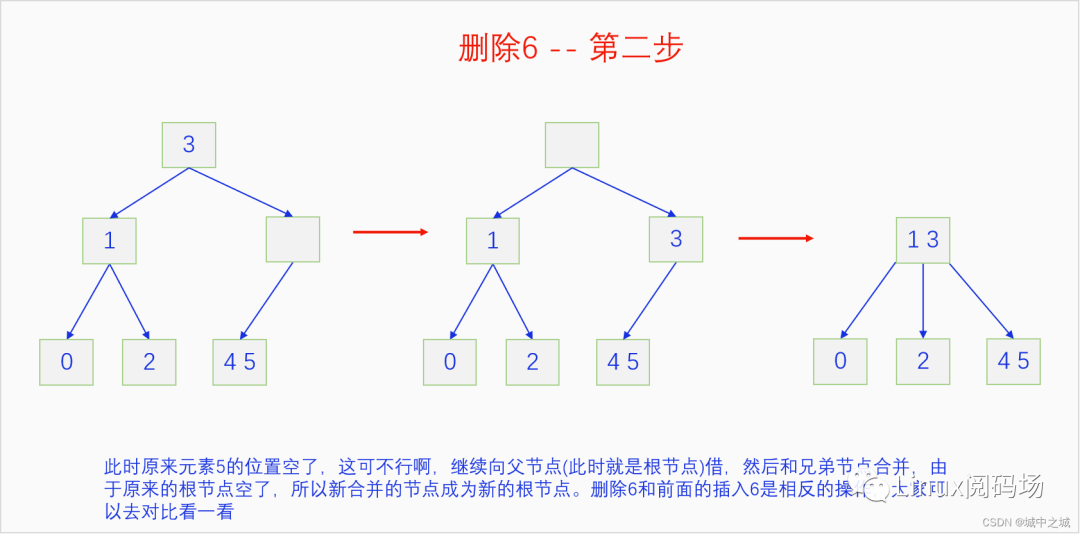
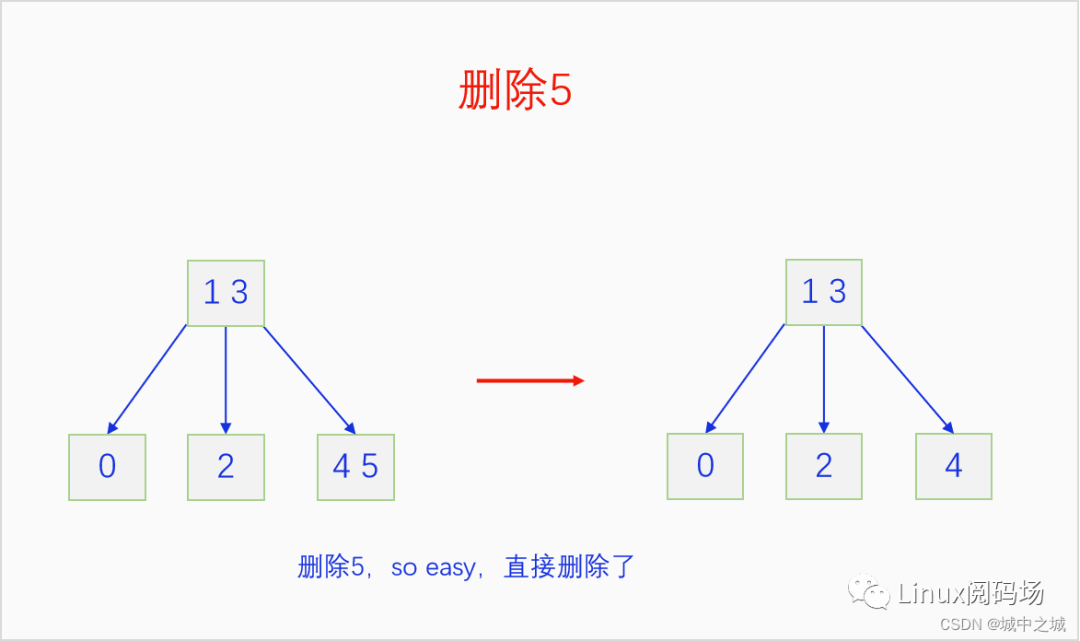
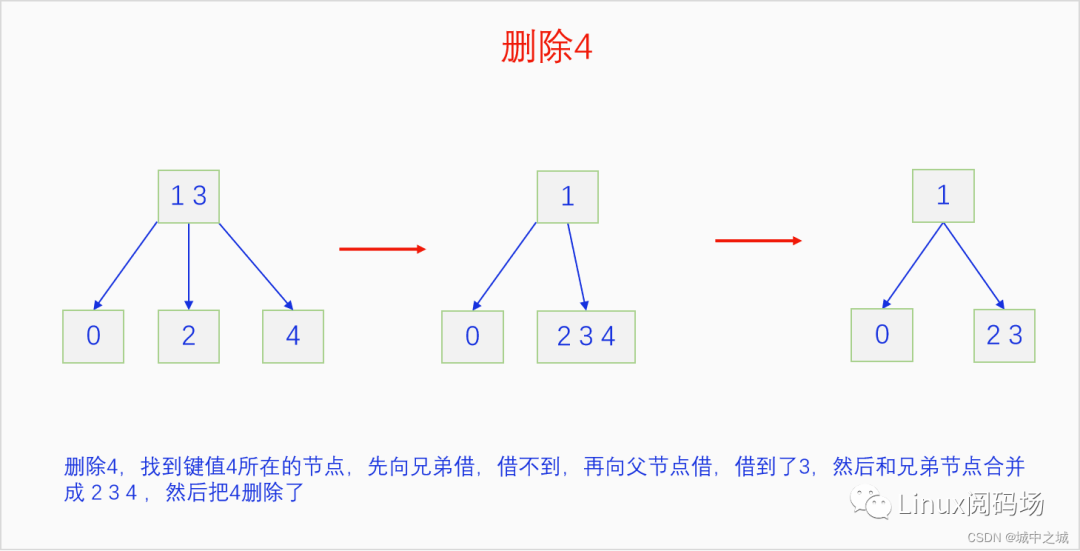
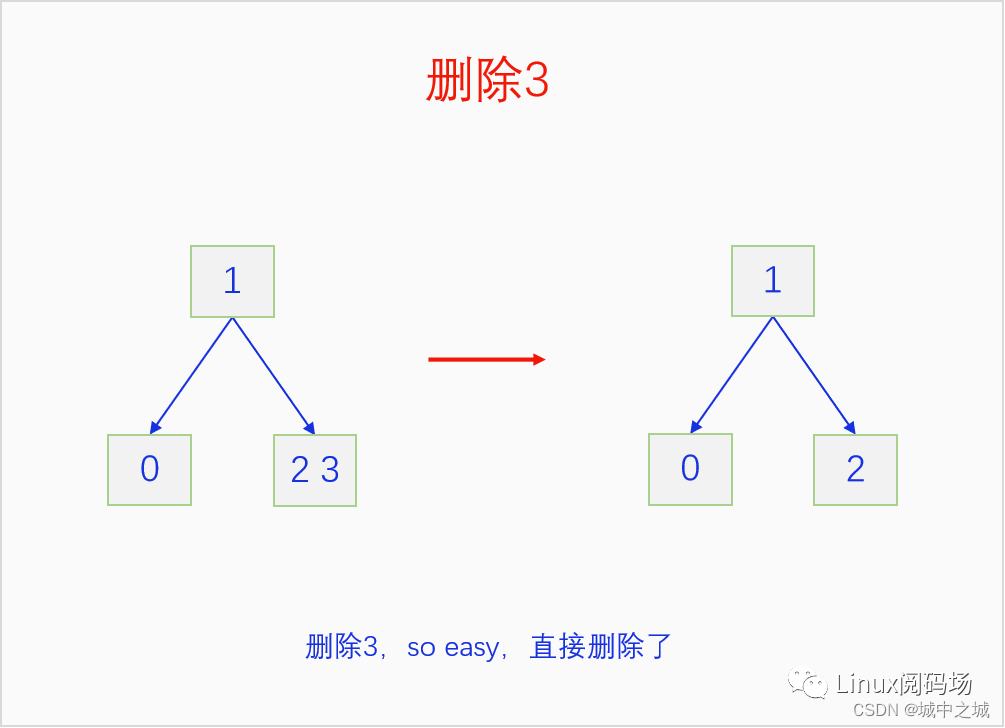
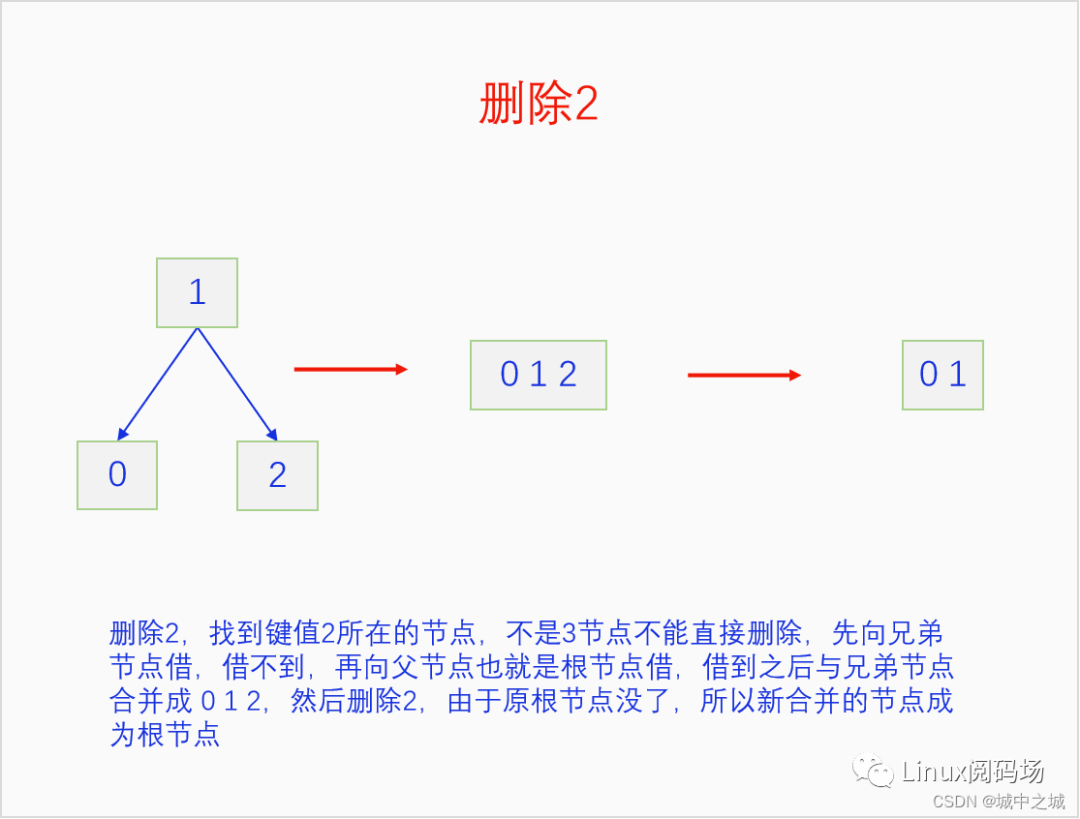
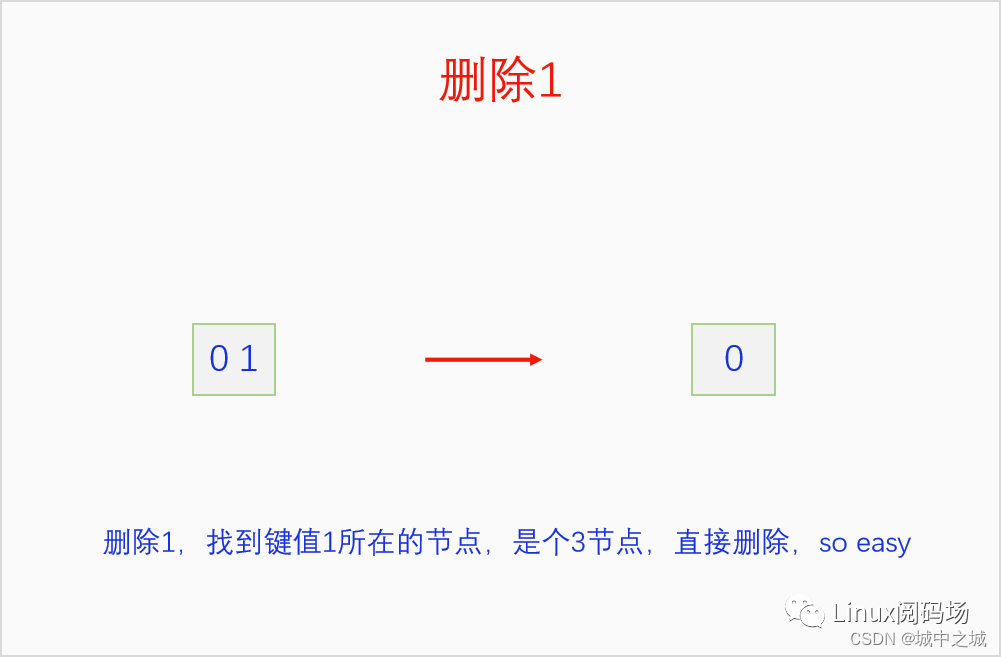
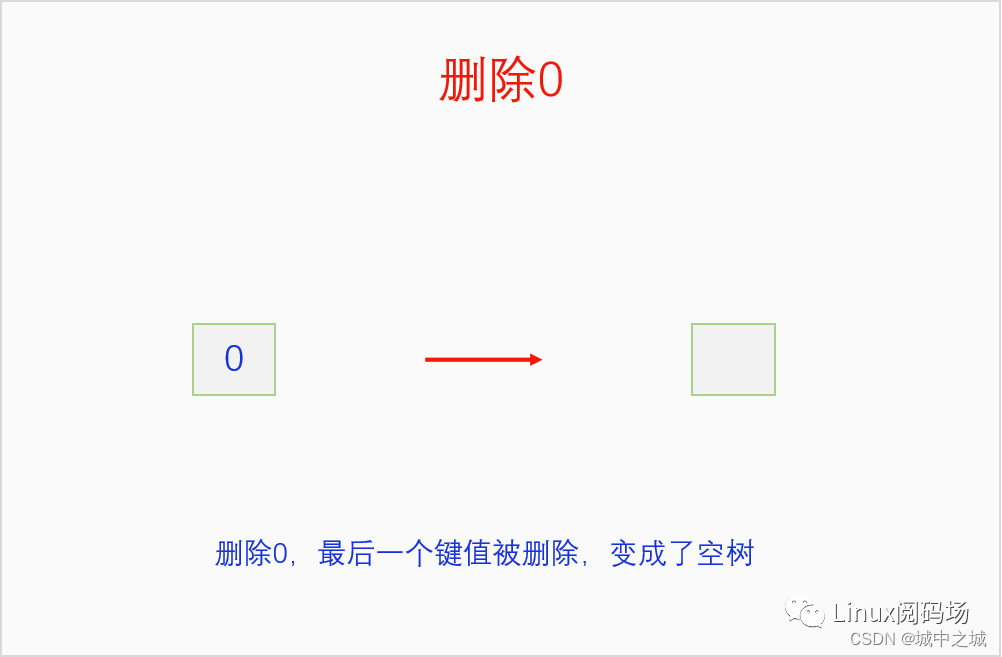
這幾幅圖詳細地講解了如何把前面建立的2-3 B樹按照9-0的鍵值順序依次刪除。但是沒有刪除中間節(jié)點的情況,我們再舉例說明一下刪除中間節(jié)點的情況。
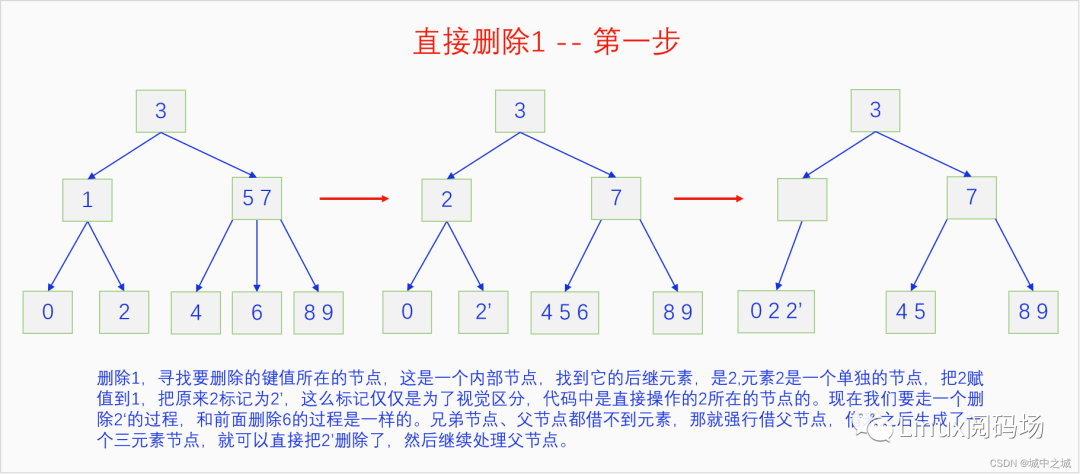
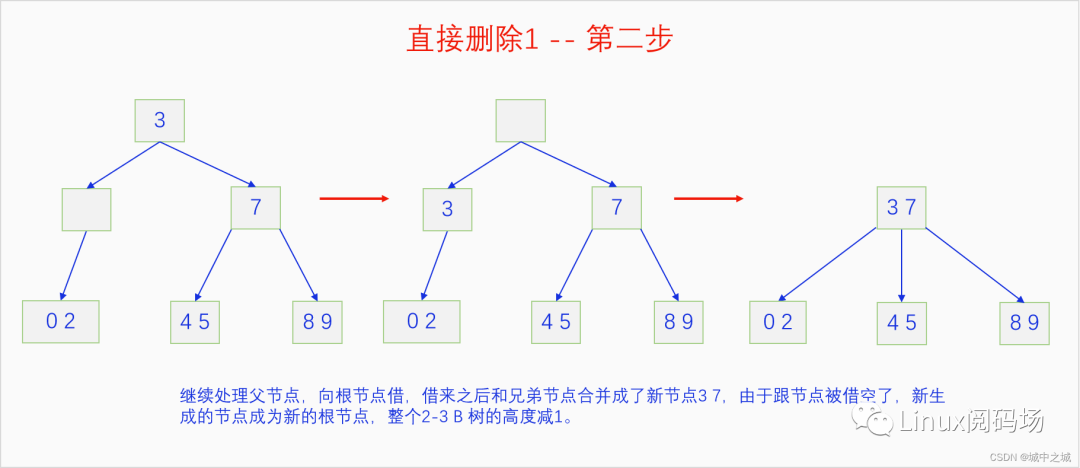
我們來解釋一下前面留下來的疑問,為啥用后繼元素覆蓋被刪除元素然后刪除后繼元素是可行的。2-3 B樹是一顆排序樹,用后繼元素覆蓋被刪除元素后,不考慮后繼元素節(jié)點,整個樹還是一顆排序樹,但是可能不是一顆2-3 B樹了,所以對后繼元素節(jié)點走個刪除流程,就能保證整個樹還是2-3 B樹。后繼元素如何尋找呢?首先我們可以發(fā)現2-3 B樹是一個完整的樹,也是說它的內部節(jié)點如果是一個單元素節(jié)點它一定存在兩個子節(jié)點,如果是一個雙元素節(jié)點,它一定存在3個子節(jié)點。對于任意內部節(jié)點的元素,我們先到這個元素緊鄰的右子節(jié)點,然后在這顆子節(jié)點樹上一直順著最左子節(jié)點找到底,就能找到我們想要的后繼元素了。
三、紅黑樹的操作邏輯
當你明白了2-3 B樹的操作邏輯之后,就基本明白了紅黑樹的操作邏輯,紅黑樹就是對2-3 B樹的模擬,2-3 B樹的一個節(jié)點可能有兩個元素,而二叉樹的每個節(jié)點都只有一個元素,那么如何模擬呢,二叉樹給每個節(jié)點加了一個顏色屬性,黑色就代表是正常的連接(圖中的黑色都是用的藍色),紅色就代表是內部連接,也就是原來的雙元素節(jié)點被分成了兩個節(jié)點,它們之間用紅色連接,代表二者本來是同一個節(jié)點的,下面我們就來看看這個模擬的過程。
我們首先來看單個節(jié)點是怎么怎么模擬的:
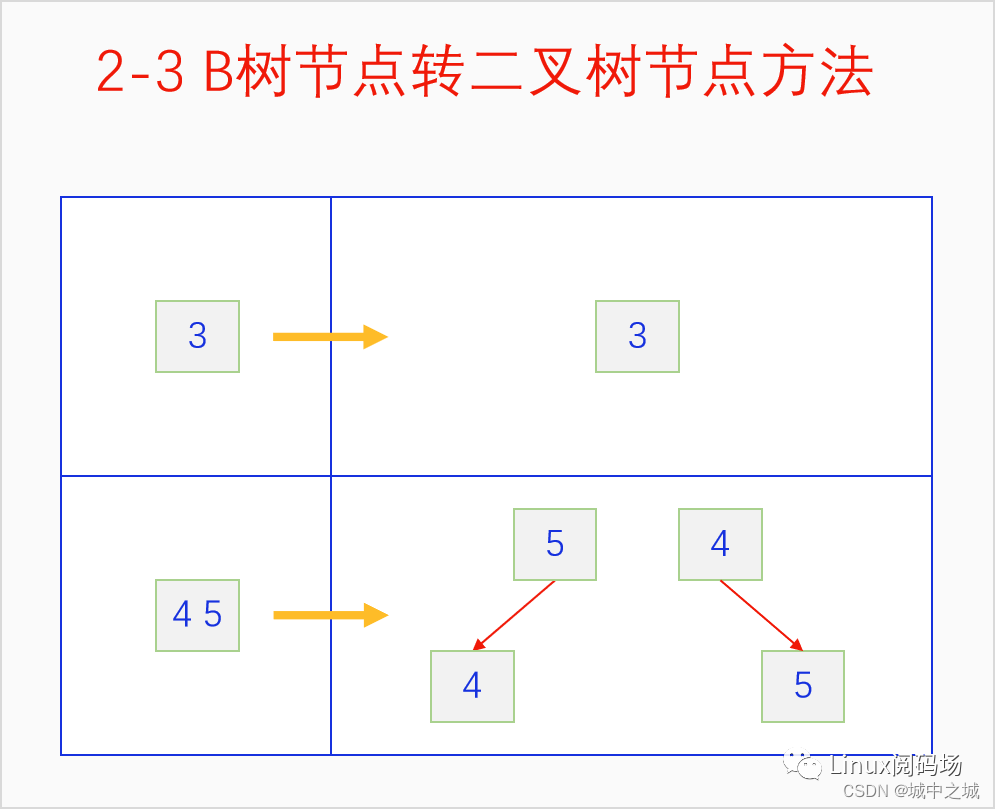
單個節(jié)點的轉換是很簡單的,單元素節(jié)點還是單元素節(jié)點,雙元素節(jié)點就有兩種轉換方式了,用哪種方式都可以,為了邏輯簡單,我們都選擇用左斜的轉換方式。我們把前面生成的2-3 B樹轉換成紅黑樹試一下。
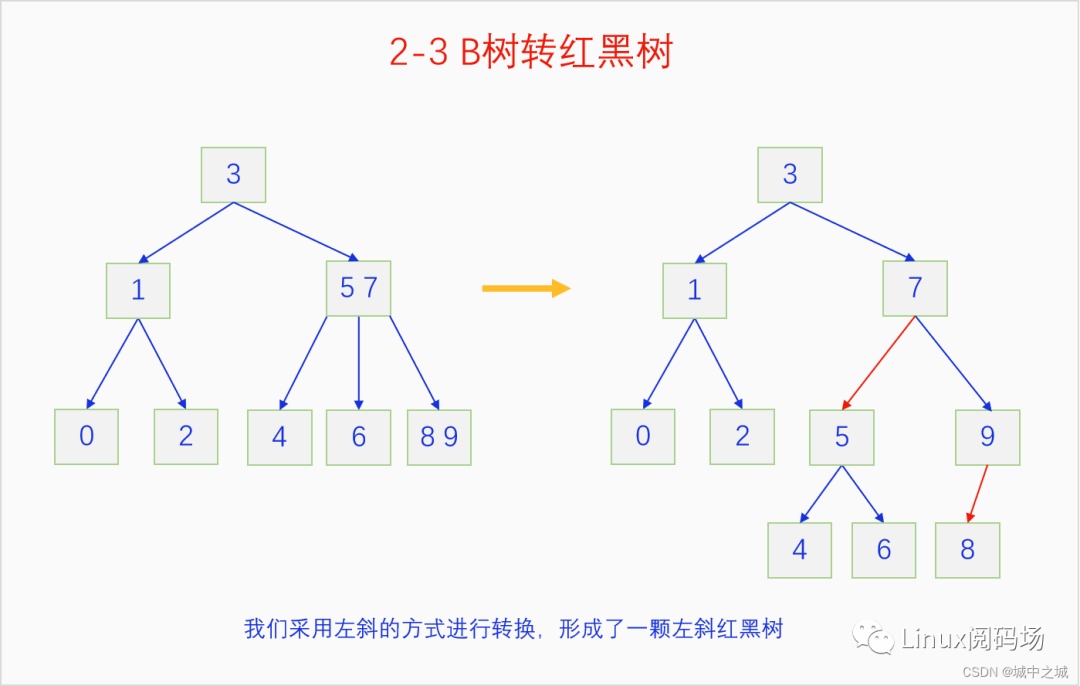
可以看到這個轉換還是很簡單的,轉換前2-3 B樹是一顆絕對平衡樹,所有的葉子節(jié)點都在同一層,轉換后雖然樹變得不太平衡了,有的葉子節(jié)點高度變高了,但是可以看出葉子最高的高度與最低的高度頂多相差一倍,所以紅黑樹是一顆相對平衡樹,相對平衡和絕對平衡都是平衡,都能保證樹的操作復雜度是O(logn)。
3.1 紅黑樹的定義
我們把2-3 B樹轉換成紅黑樹之后能不能對這個紅黑樹任意操作呢?不能,因為任意操作之后可能就無法再轉換回2-3 B樹了,這就意味著這個紅黑樹可能不是平衡樹了。因此我們要對紅黑樹進行定義,把對紅黑樹的操作限制在定義允許的范圍內,這樣紅黑樹就永遠是紅黑樹,就一定對應著一顆2-3 B樹,就一定是一顆平衡樹。下面我們來看一下紅黑樹的定義。
所有的節(jié)點不是黑色的就是紅色的
根節(jié)點是黑色的
所有葉子節(jié)點是黑色的
從每個葉子到根的所有路徑上不能有兩個連續(xù)的紅色結點
從任一結點到其每個葉子的所有路徑都包含相同數目的黑色結點
我們來分析這5條定義,1.所有節(jié)點都是黑色的或者紅色的,這是肯定的了,要不然能叫紅黑樹嘛。2.根節(jié)點是黑色的,這是肯定的了,紅色節(jié)點的含義是自己與父節(jié)點的連接是紅色的,也就是說自己和父節(jié)點是內部節(jié)點,根節(jié)點沒有父節(jié)點,只能是黑色的。3.所有的葉子節(jié)點都是黑色的,紅黑樹里規(guī)定把本來的每個葉子節(jié)點的左右子節(jié)點的那個空指針看做是NULL節(jié)點,看成是葉子節(jié)點,規(guī)定NULL節(jié)點是黑色的,這個規(guī)定好像沒啥用,沒有看出來這個規(guī)定的邏輯意義或者實現意義。4.從每個葉子到根的所有路徑上不能有兩個連續(xù)的紅色結點,這一條是保證2-3 B樹的每個節(jié)點都是2節(jié)點或者3節(jié)點。5.從任一結點到其每個葉子的所有路徑都包含相同數目的黑色結點,這一條是保證2-3 B樹的所有葉子節(jié)點都是等高的。
有了紅黑樹的這五條定義就能保證紅黑樹永遠是紅黑樹,永遠都對應著一顆2-3 B樹,永遠都是一顆平衡樹。這5條定義怎么記憶呢?我總結了4個四字短語來記憶,非紅即黑、根黑葉黑、紅子不紅、黑徑相等。
紅黑樹的定義只是給我提供了限制,我們的操作不能違背這個限制,但是紅黑樹的定義并沒有告訴我們怎么操作紅黑樹,只要你的實現方法符合定義就行,下面我們來看一看紅黑樹應該如何操作。
3.2 紅黑樹的旋轉與翻色
我們構建一顆紅黑樹并不是從2-3 B 樹轉換過來的,而是從一個空樹,按照紅黑樹的構建規(guī)則不斷地插入和刪除而產生的一顆紅黑樹,在這個過程會出現很多的3元素節(jié)點需要我們來處理。一個3元素節(jié)點會對應怎樣的紅黑樹片段呢,我們會遇到怎樣的情況呢,遇到了又應該怎么處理呢,下面我們來看一下。
3元素節(jié)點的處理是紅黑樹的重點,也是難點,掌握了這個也就基本掌握了紅黑樹。
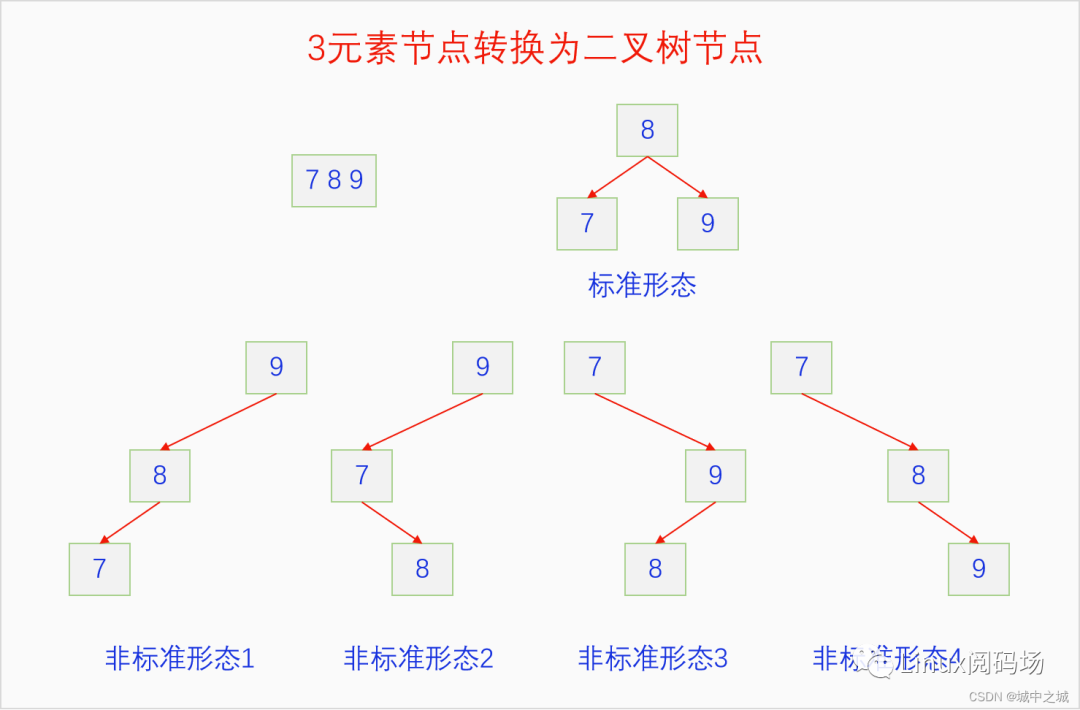
3元素節(jié)點轉換為二叉樹節(jié)點會有這五種可能的情況,當然我們不會把3元素節(jié)點轉換成奇奇怪怪的形態(tài),我們一般會把3元素節(jié)點轉換成標準形態(tài),這樣比較好處理。但是我們在處理紅黑樹的過程中也會遇到這四種非標準形態(tài),如果遇到的話,就用下面的方法把它們轉為標準形態(tài)再進行翻色就可以了。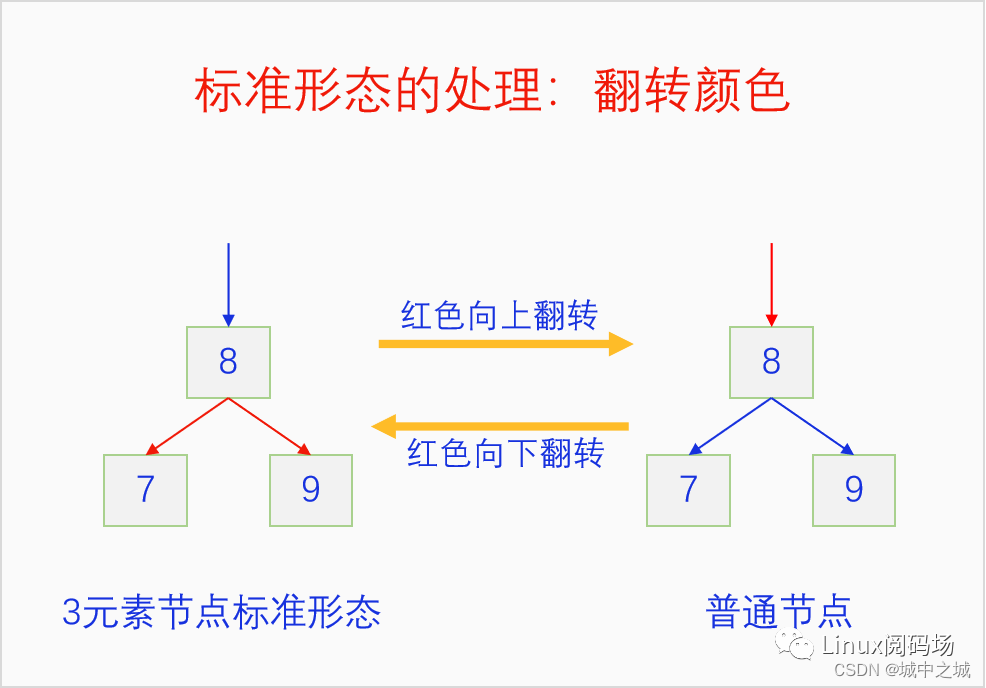
標準形態(tài)本身并沒有違背紅黑樹的定義,所以紅黑樹中可以存在標準形態(tài)。但是本文用的是2-3 B樹模型,遇到了標準形態(tài)都會進行翻色處理,所以最終的紅黑樹上不會有標準形態(tài)的,只有中間的處理過程中會產生標準形態(tài)。翻轉顏色(color flip)這個操作,不違背紅黑樹的前三條定義,也不違背黑徑相等的定義,但是有可能違背紅子不紅的定義。這是因為所有過7 8 的路徑以前有一個黑徑,現在還是一個,對于過8 9的路徑也是如此,翻轉前后過7 8和8 9的路徑和黑色節(jié)點數不會發(fā)生變化。翻色分為向上翻色和向下翻色,向上翻色用于插入操作中,有可能會違背紅子不紅的規(guī)定,因為8的父節(jié)點有可能還是紅色的,所以對這個問題要一直往上回溯處理。向下翻色用于刪除操作中,不會違背紅子不紅的定義。
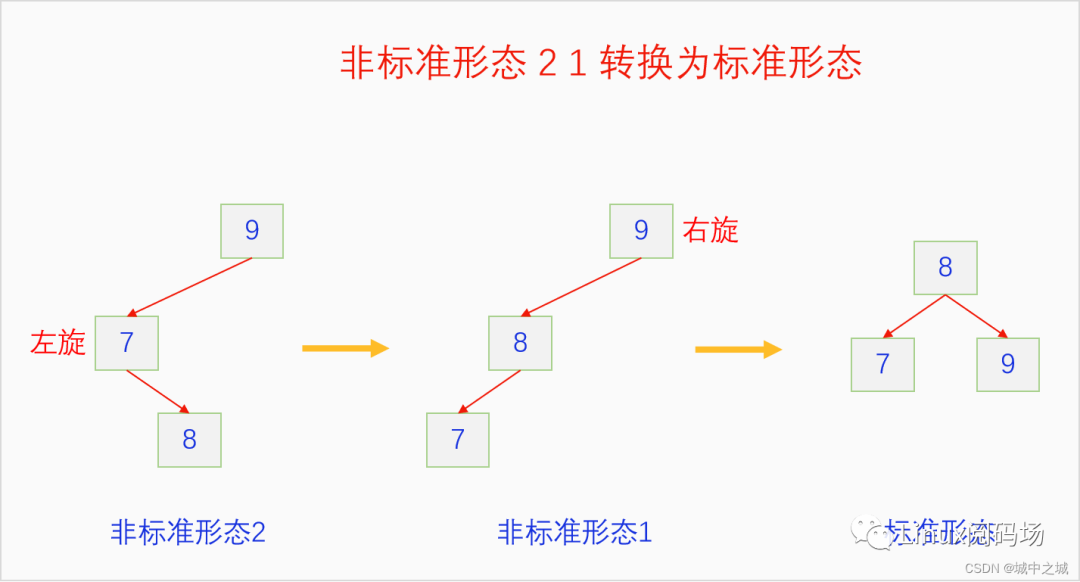

可以看到非標準形態(tài)可以通過一次左旋和一次右旋轉換成標準形態(tài)。那么自旋又是怎么操作的呢?
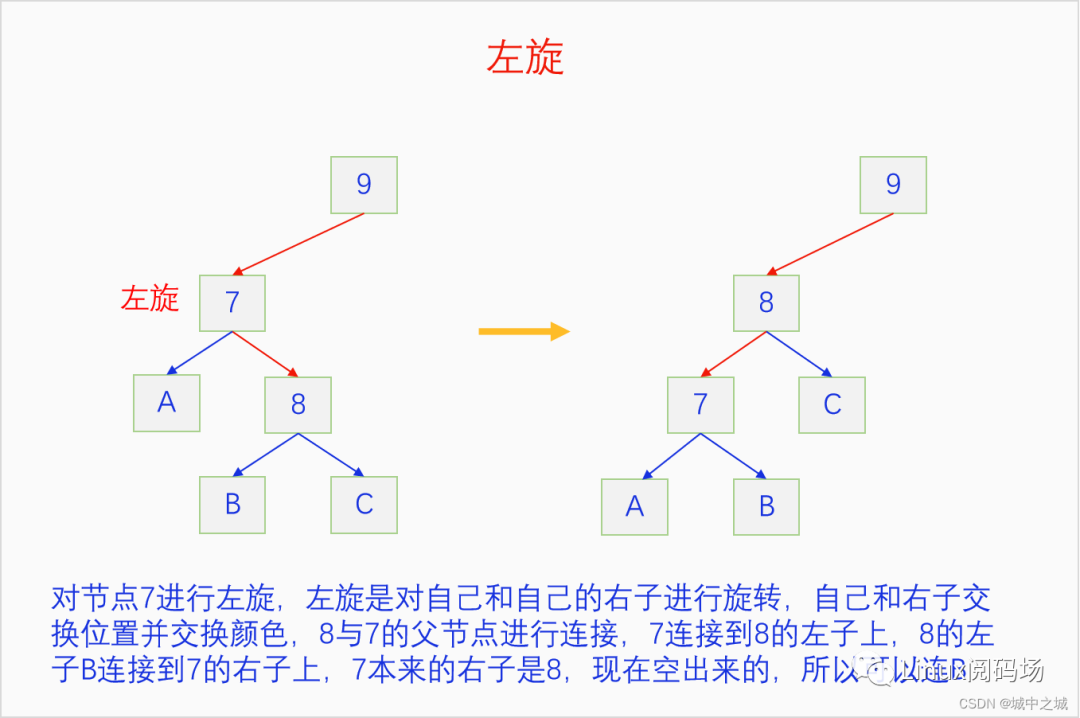
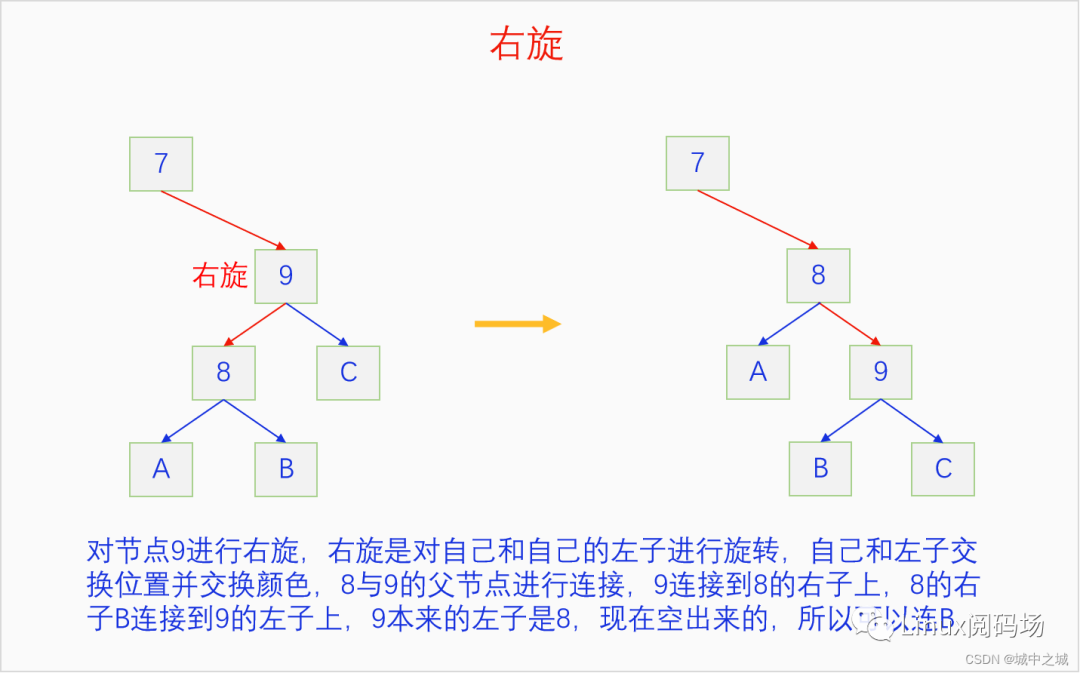
從B樹的角度來看左旋和右旋,左旋右旋改變的是一個節(jié)點內部的連接,并沒有改變B樹本身任何的性質。從二叉樹的角度來看,左旋右旋不會改變紅子不紅的問題,原來有紅子不紅的現在還繼續(xù)有,原來沒有現在還沒有。通過數過A B C的路徑的黑徑數可以發(fā)現其前后不變,所以左旋右旋沒有違背紅黑樹黑徑相等的定義。當我們把旋轉和翻色都學明白之后就可以開始研究紅黑樹是怎么模擬2-3 B樹的插入操作了。
3.3 紅黑樹的插入操作
本文實現的是左斜紅黑樹,也就是所有的紅色節(jié)點都是左子節(jié)點。紅黑樹插入的時候節(jié)點默認顏色是紅色,這個和2-3 B樹的所有鍵值只插入葉子節(jié)點是一致的,而且增加一個末端的紅色節(jié)點不會違背紅黑樹黑徑相等的定義,但是有可能違背紅色不紅的定義,所以要通過旋轉和翻色來解決這個問題,并要遞歸解決這個問題,直至根節(jié)點。節(jié)點插入之后首先要先考慮自己是否構成3元素節(jié)點,如果不構成的話就結束了,如果構成的話,就要進行處理,構成的條件是父節(jié)點是紅色或者父節(jié)點的另一個子節(jié)點是紅色,如果兩個子節(jié)點都是紅色就要進行翻色處理,如果子節(jié)點和父節(jié)點是紅色節(jié)點,則要按照前面說的非標準形態(tài)進行處理,先轉換成標準形態(tài),再進行翻色。處理完成之后繼續(xù)對父節(jié)點進行同樣的處理,直至根節(jié)點。
下面我們來看一看紅黑樹模擬2-3 B樹的插入操作的過程,加深對紅黑樹插入操作地理解。
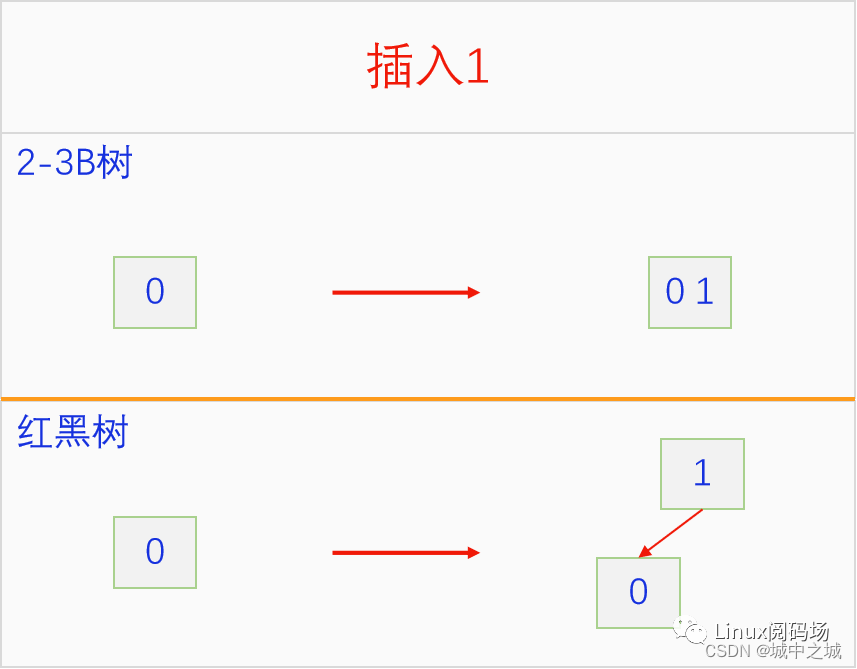
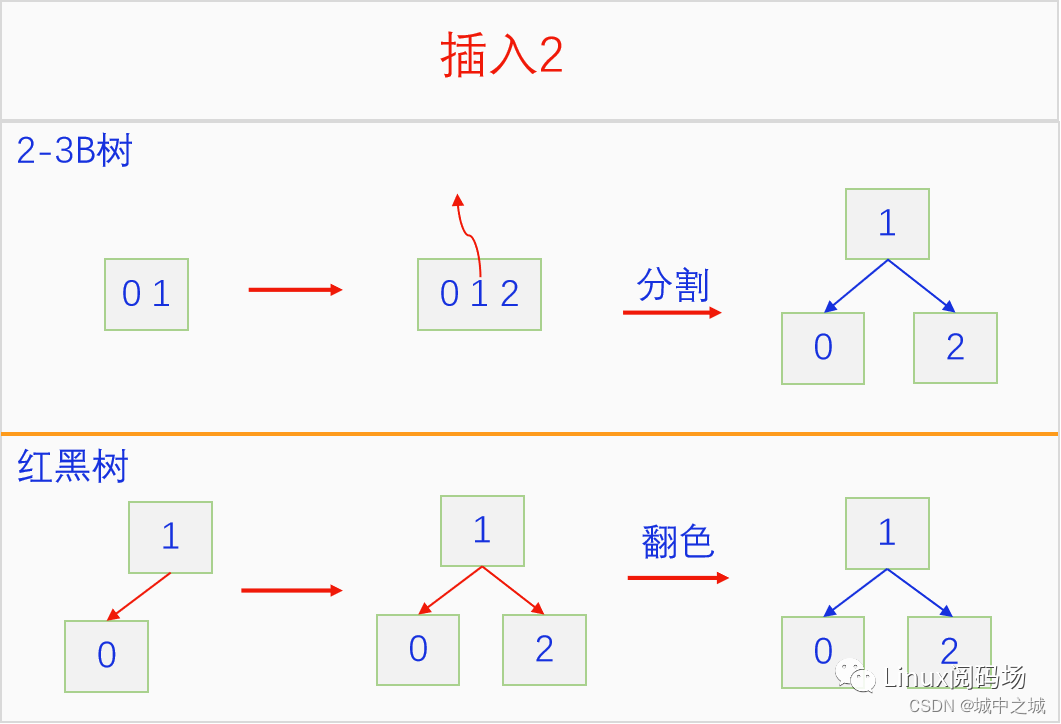
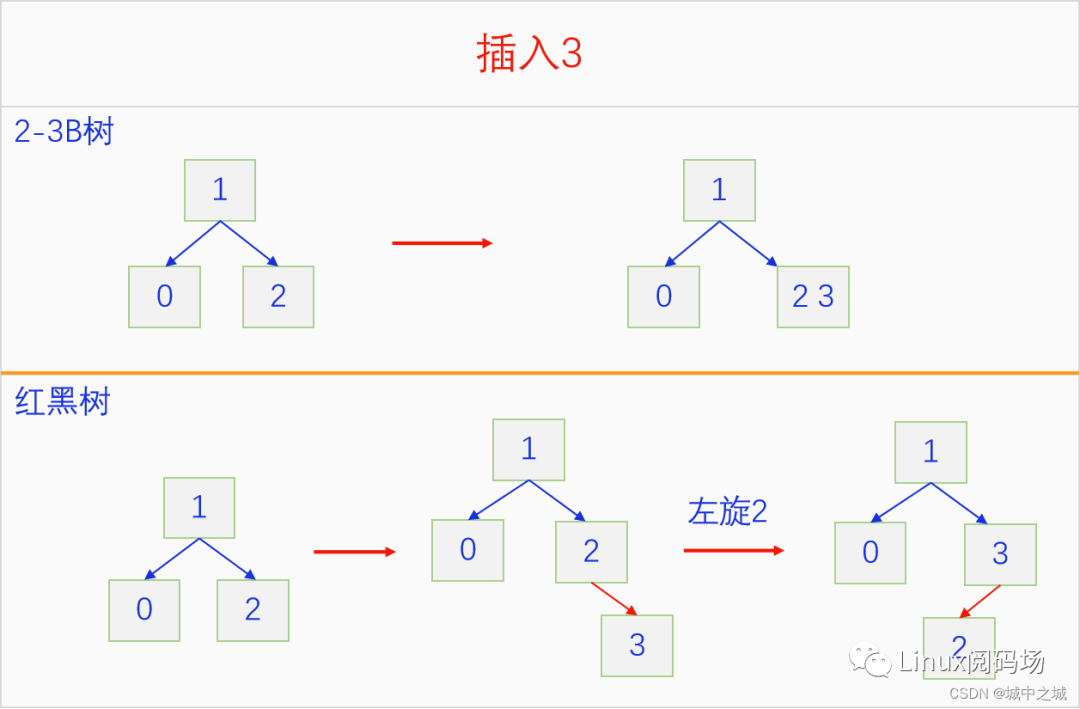
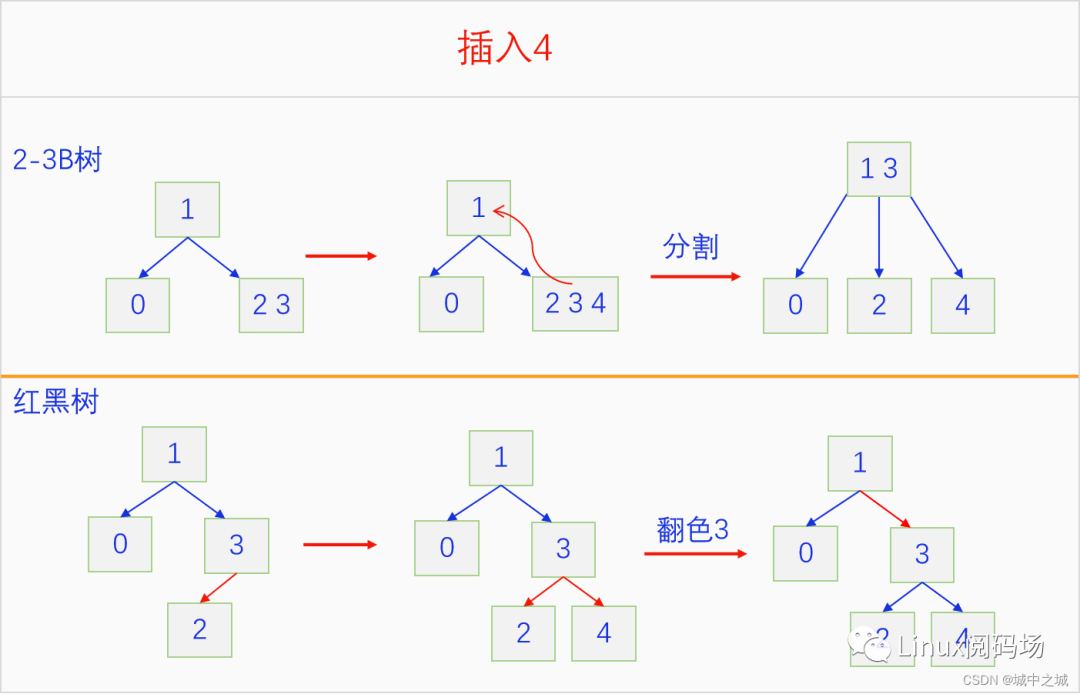
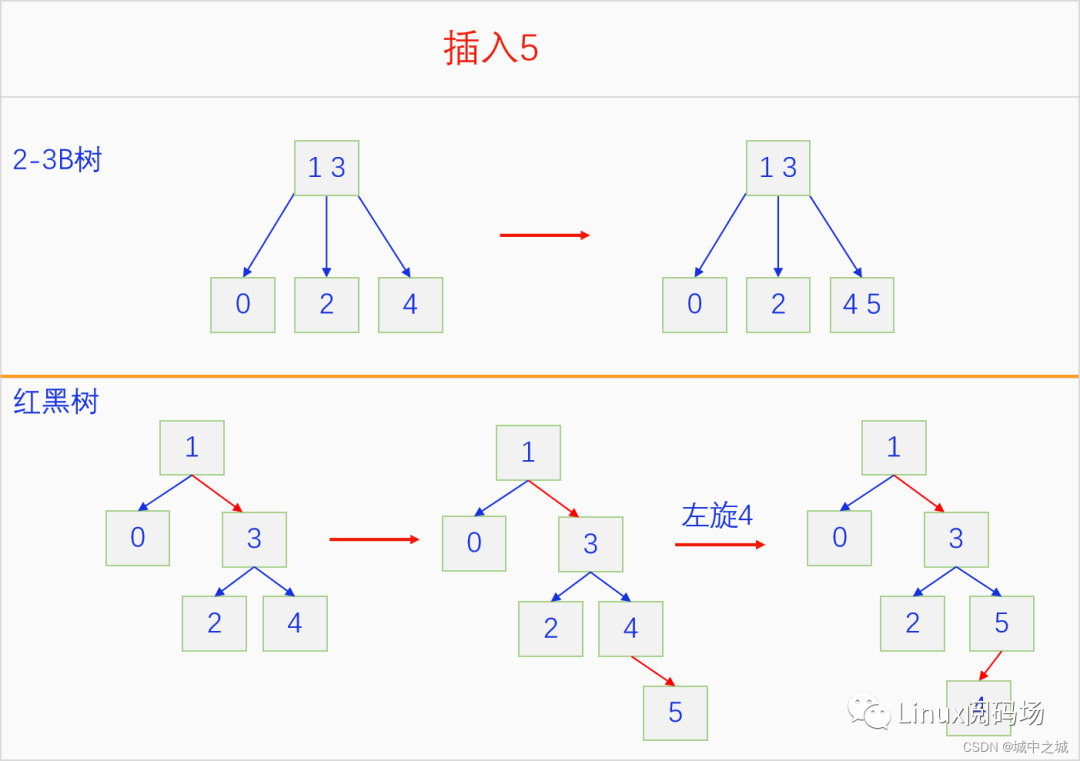
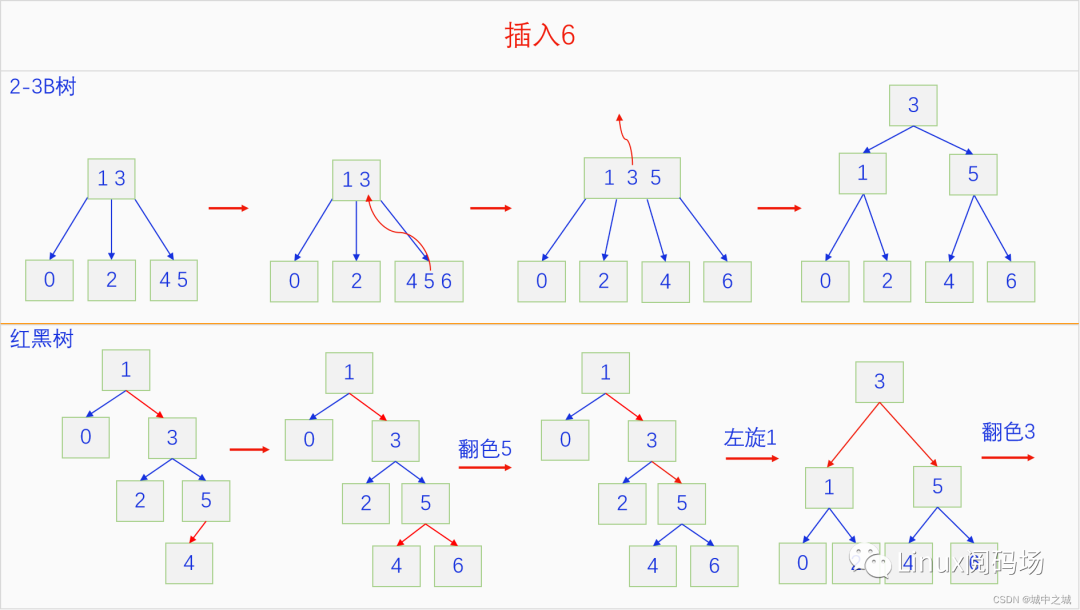
可以看出紅黑樹一直都在進行尋找3元素節(jié)點,也就是兩個連續(xù)的紅色或者相鄰的紅色,然后進行旋轉和翻色操作,直至整個紅黑樹都符合紅子不紅的定義為止。
3.4 紅黑樹的刪除操作
紅黑樹的刪除操作比較復雜,分為很多種情況,我們先來看幾個示例
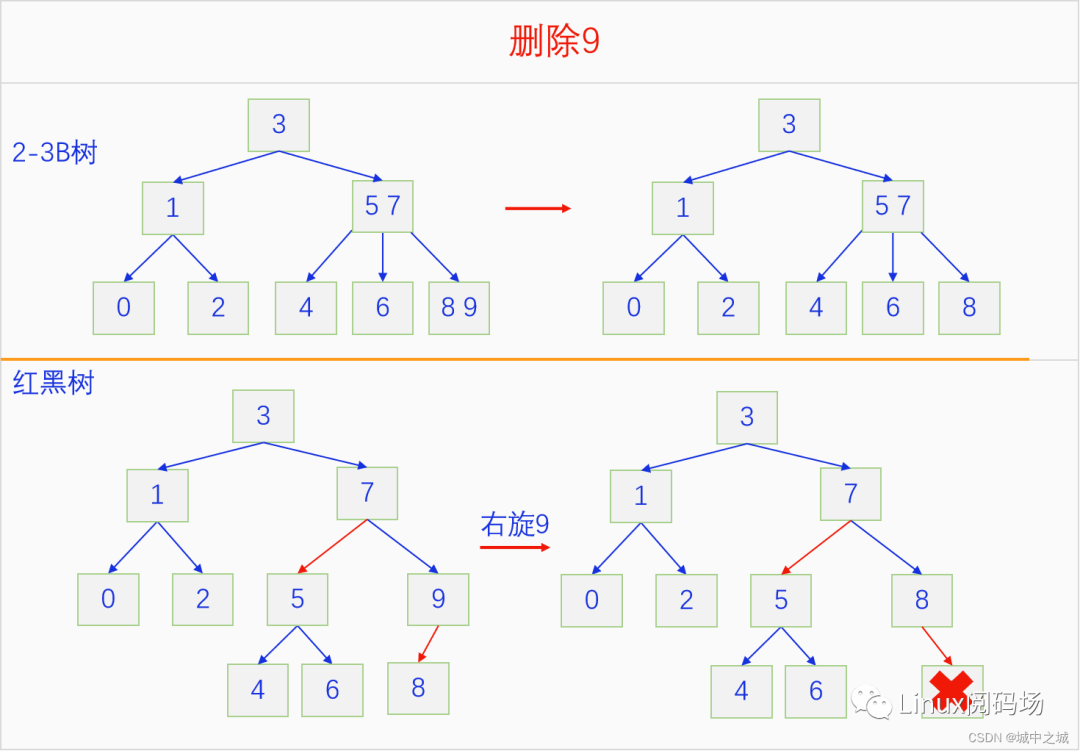
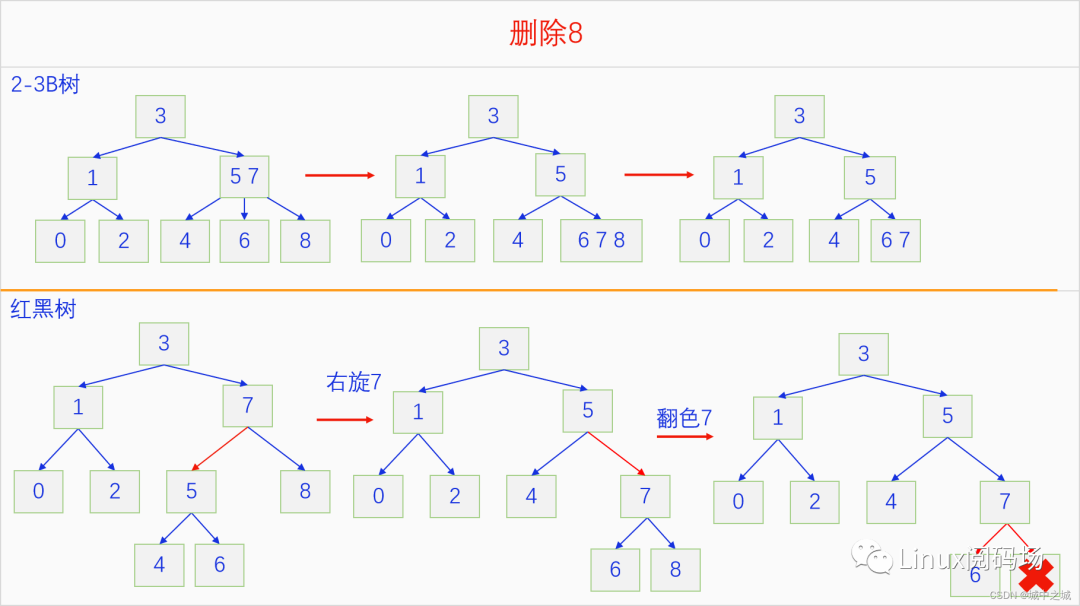
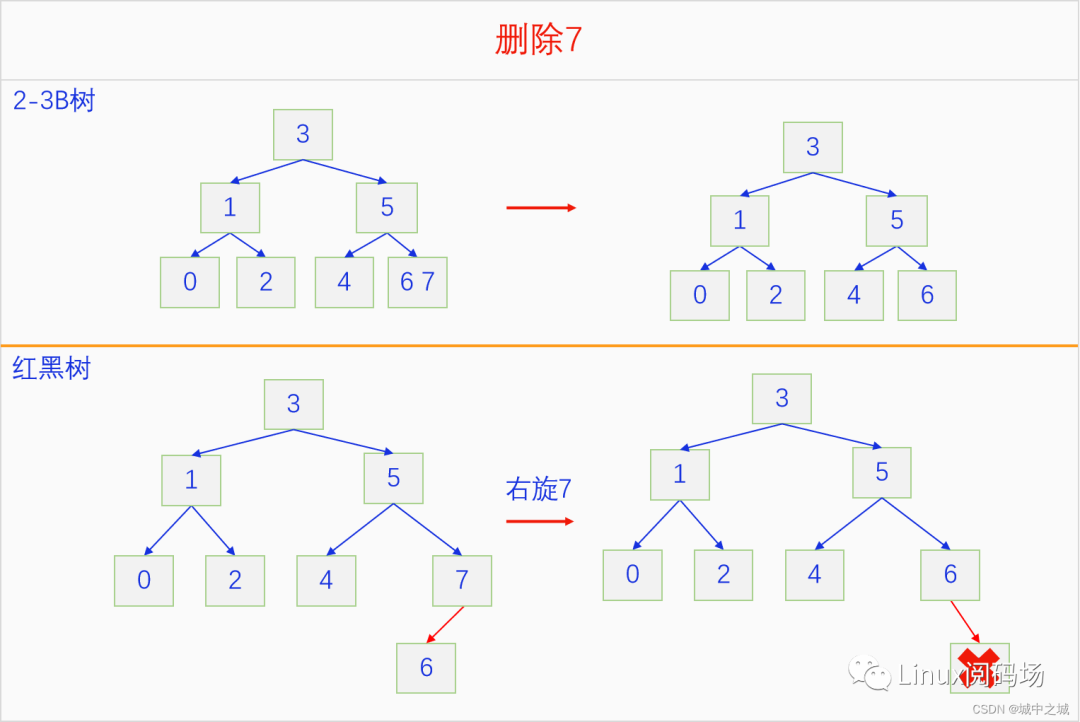
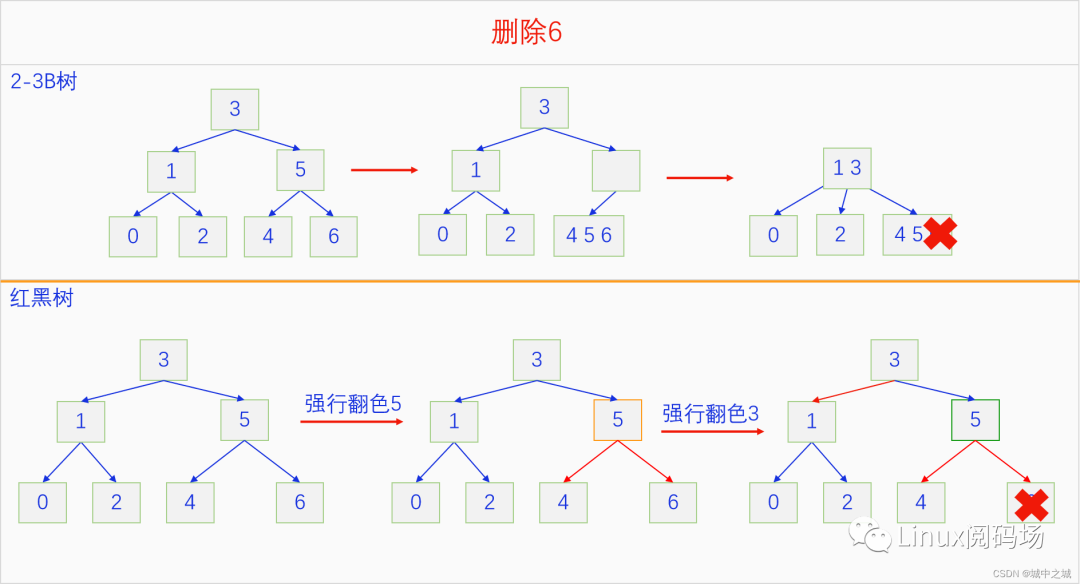
紅黑樹的刪除有很多種情況,最簡單的就是要刪除的節(jié)點是葉子節(jié)點并且是紅色,直接刪除就行了,然后是自己沒有右子,自己的左子是紅色,和左子做一個右旋就變成了前面的情況,可以直接把自己刪除。如果這兩種情況都不是,那就想辦法把自己變成紅色節(jié)點了,對應2-3 B樹中的操作就是借元素。紅黑樹的刪除過程還有一些更復雜的過程,我們在下一章實現里面再細說。
四、紅黑樹的實現
理解了上面大部分的邏輯之后,我們就可以開始去實現紅黑樹了,本文用C語言實現了2-3 B樹對應的左斜紅黑樹。
4.1 結構體定義
首先我們要定義紅黑樹的結構體和接口。
rbtree.h
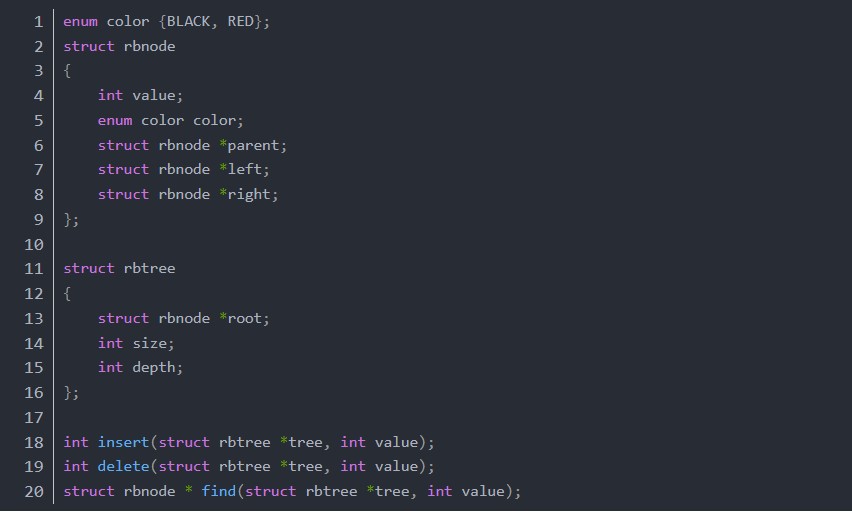
這個文件也很簡單,定義了紅黑樹節(jié)點rbnode,顏色枚舉值RED BLACK,以及rbtree,rbtree用來放置紅黑樹的根節(jié)點和一些其它信息。還聲明了紅黑樹的三個接口函數insert、delete 和 find。
對于紅黑樹來說,find的實現很簡單,二叉搜索樹的查找:
rbtree.c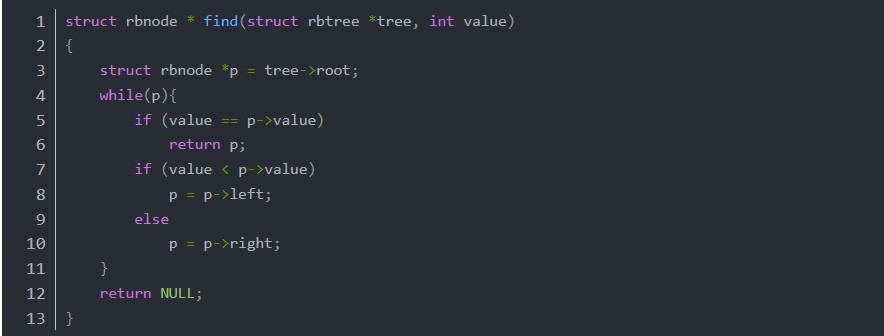
紅黑樹本身也是個二叉搜索樹,所以它的查找函數和二叉搜索樹的查找是一樣的。
4.2 翻色與旋轉代碼
下面我們來說下翻色與旋轉函數的實現
rbtree.c
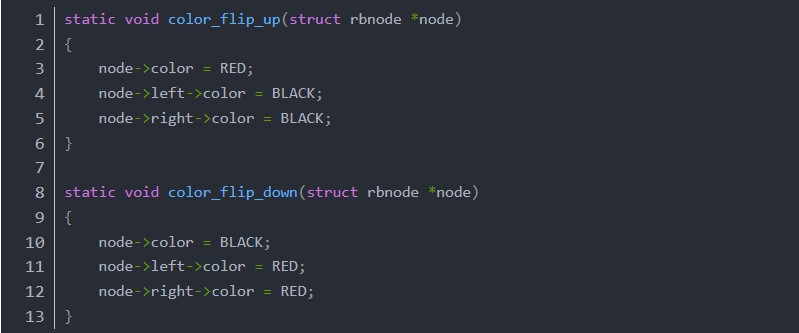
翻色函數很好理解,向上翻色就是把自己變紅,把左子和右子都變紅,向下翻色正好相反。
再來看一下旋轉函數
rbtree.c
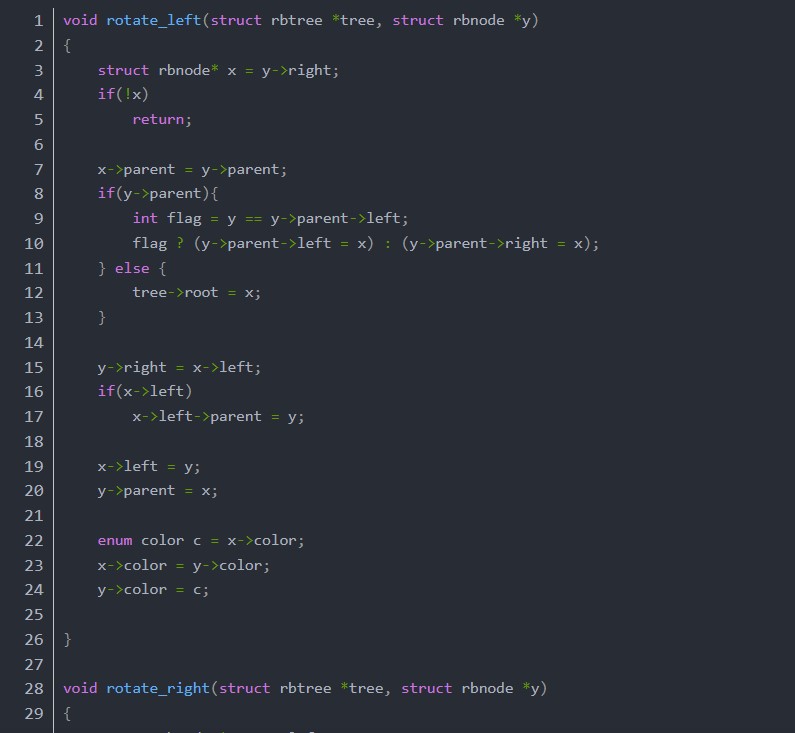
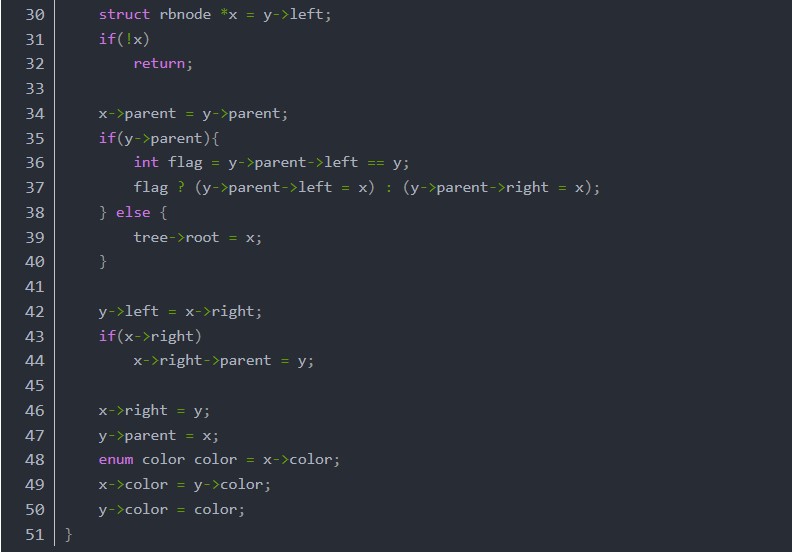
我們以左旋為例講解一下。左旋旋轉的是自己和右子,往左旋把自己旋下去了,把右子旋上來了,右子占據了自己的位置,自己成了右子的左子。函數首先做的是交接parent,把右子先掛到parent上去,然后把右子的左子掛接到自己身上,接著讓自己成為右子的左子,最后交換二者的顏色,這么做是為了保持兩者的連接顏色不變。右旋的邏輯是類似的,這里就不再多講解了。
4.3 插入操作的代碼
代碼如下,主要是兩個函數,insert和insert_fix。
rbtree.c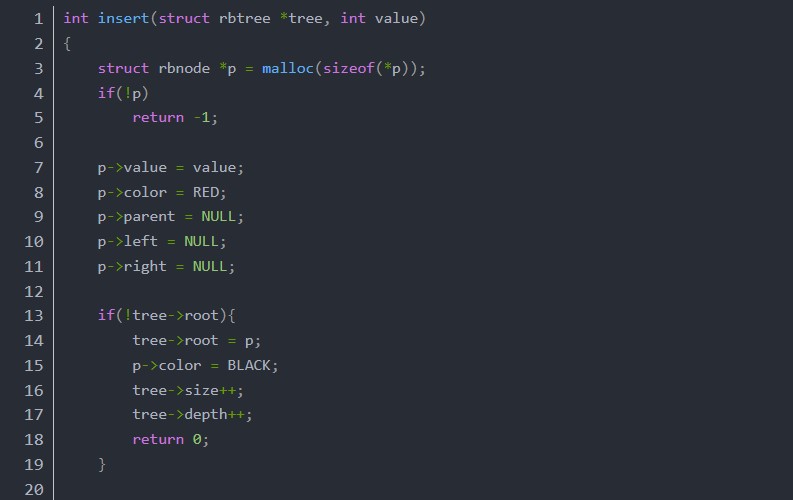
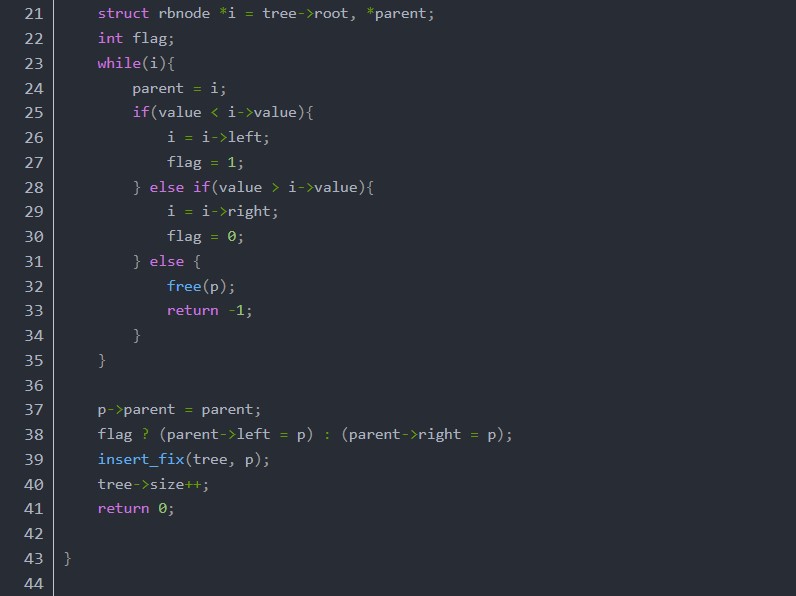
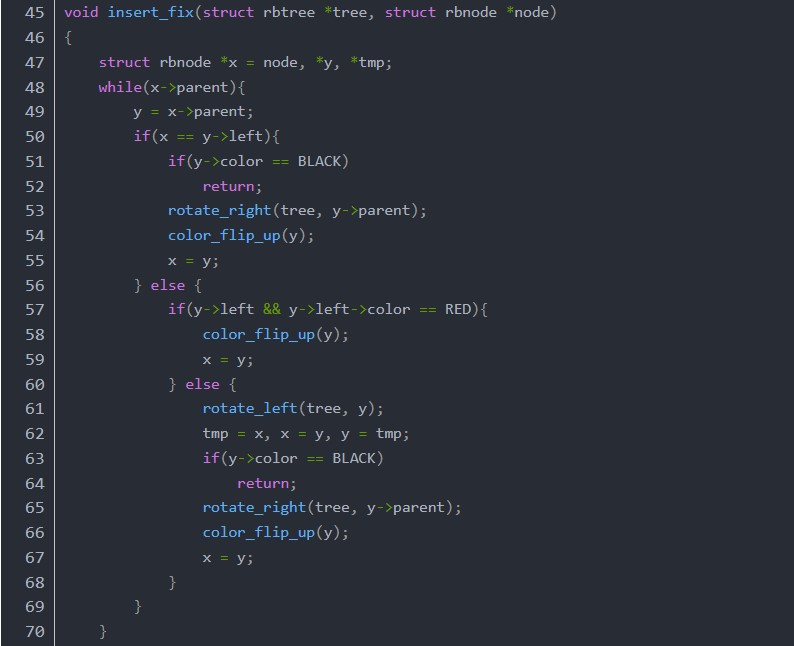

函數insert的邏輯很簡單,就是創(chuàng)建新的節(jié)點,新節(jié)點的顏色設為紅色,按照二叉搜索樹的方式尋找要插入的位置,然后調用insert_fix,來保證整個樹是一個符合定義的紅黑樹。insert_fix的實現主體是一個while循環(huán),當x的parent存在時就一直循環(huán),直到x是根節(jié)點為止,當然while內部有提前結束循環(huán)的地方。進入循環(huán)體內,首先我們要明白的就是,此時x的顏色是RED,這是因為第一次循環(huán)的時候x是RED的,后面循環(huán)再次進來的時候x也是RED的,如果不是的話就不會繼續(xù)循環(huán)了。先分x是左子還是右子兩種情況來討論,當x是左子的時候,看parent是不是RED,如果是BLACK的話,直接return。如果是RED的話,此時x和y都是左斜的,y是左斜的是因為我們實現的是左斜紅黑樹,原有的紅色節(jié)點只可能是左斜的。對于雙紅色左斜節(jié)點的處理,我把圖片又放到下面了,大家可以再看一看。這種情況我們應當對y的parent進行右旋,右旋之后,y成了兩個紅色節(jié)點的父節(jié)點,由于旋轉之前y是紅色,所以y的parent不可能是紅色,只能是黑色,所以旋轉之后交換了顏色,所以此時y肯定是黑色。y是黑色,左子右子都是紅色,正好可以翻色,翻色之后,左子右子都變成了黑色,y變成了紅色,讓x=y進行下一輪循環(huán)。當x是右子的時候,先看一下左兄弟是不是紅色,如果是的話,父節(jié)點y肯定是黑色,正好可以翻色,對y進行翻色,讓x=y,繼續(xù)下一輪循環(huán)。如果x的左兄弟不是紅色的,先左旋y,左旋之后x y的父子關系變了,交換一下它們的值,讓x仍然是子,y仍然是父。判斷y的顏色,如果是黑色直接return函數結束,如果是紅色,x y又形成了雙左斜紅色的情況,和上面的處理方式是一樣的,右旋y的parent,翻色y,讓x=y,繼續(xù)下一輪循環(huán)。函數最后判斷根節(jié)點是否為紅色,如果為紅色的話,說明之前的根節(jié)點經歷過分割,樹的高度增加1,再把根節(jié)點重置為黑色。

4.4 刪除操作的代碼
刪除操作主要有兩個函數,delete 和 delete_fix,delete比insert稍微復雜一點,要處理被刪除的點不是葉子節(jié)點的情況。對于非葉子節(jié)點的情況,其右子樹一定存在,用右子樹的最小值,也就是右子樹的最左子節(jié)點的值覆蓋自己,然后刪除右子樹的最左子節(jié)點就可以了。
rbtree.c
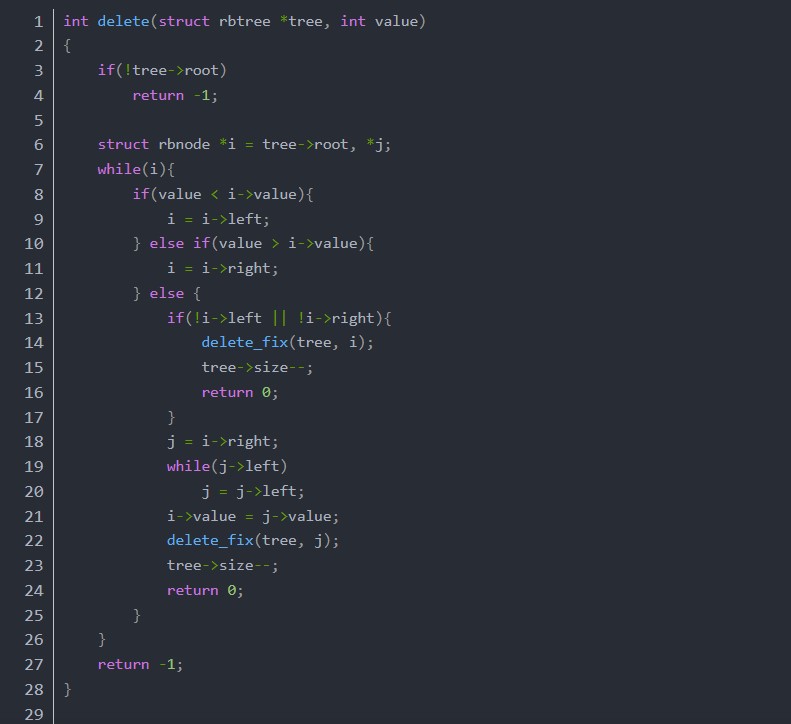
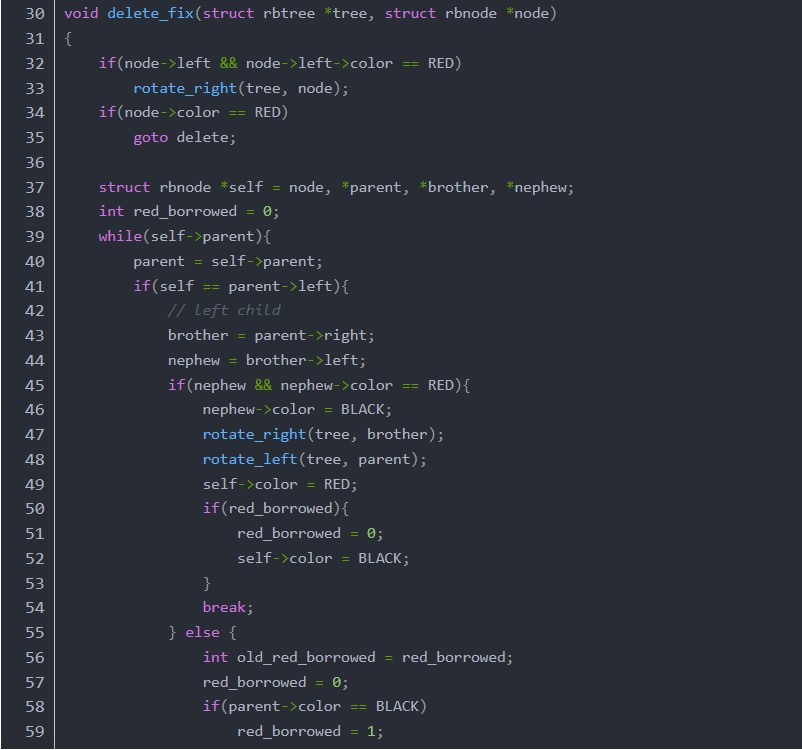
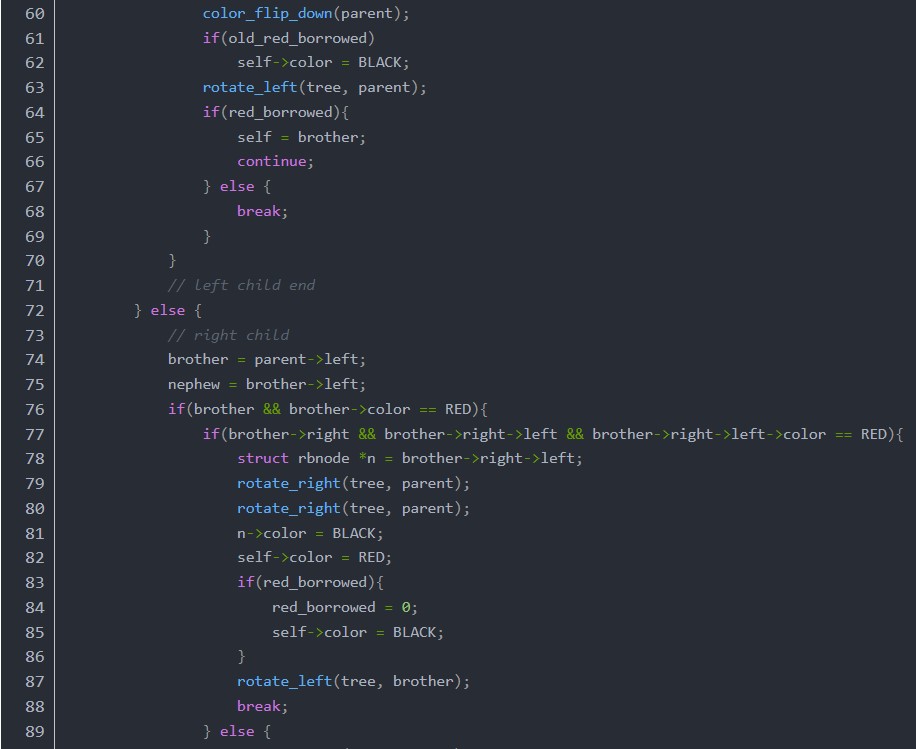
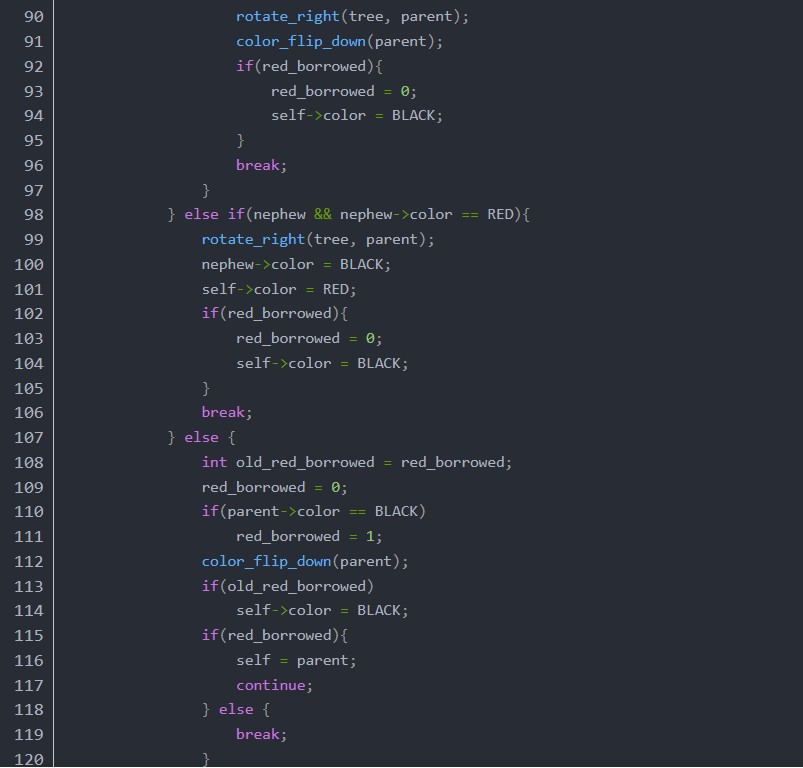
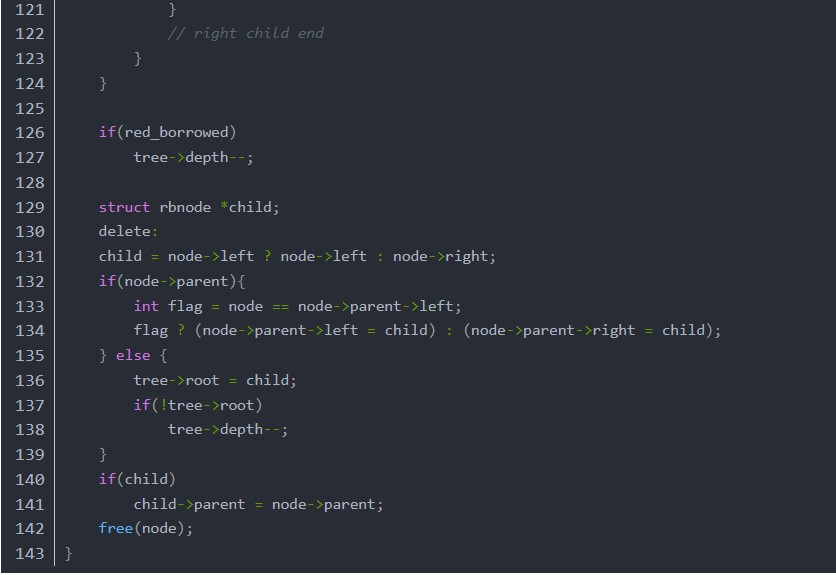
函數delete_fix首先考慮兩種特殊情況,如果node是紅色的,或者node的左子是紅色的,直接右旋自己,把自己變成紅色,然后直接goto delete。剩下的情況就是node不是紅色的,也是說node是單元素節(jié)點,要想辦法把自己變成紅色的,也就是通過借元素變成雙元素節(jié)點。進入循環(huán)的條件是當前元素的parent不為空,循環(huán)內部有一個變量red_borrowed控制著是否繼續(xù)循環(huán),如果為1則循環(huán),如果為0則結束循環(huán),也就是說循環(huán)至少會執(zhí)行一次,然后x->parent和red_borrowed共同決定是否繼續(xù)循環(huán)。循環(huán)體內分為兩種情況,自己是左子和自己是右子的情況,自己是左子的情況又分兩種,自己是右子的情況又分四種。下面通過畫圖給大家解析一下。字母與代碼中對應的節(jié)點如下:
x:self
y:parent
z:brother
w:nephew(侄子)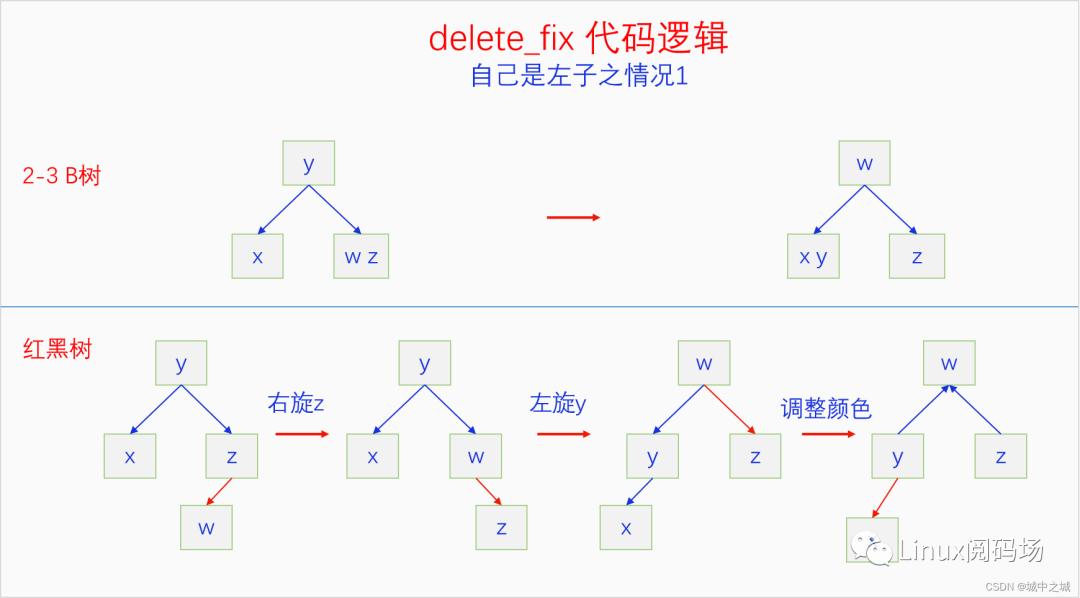
注意在每次循環(huán)開始的時候x都是黑色的。由于我們是左斜紅黑樹,所以z不可能是紅色的,可能的情況只有w是紅色的或者是黑色的(下一種情況),對于這種情況,我們通過其對應的2-3 B樹可以看出來我們應該如何把紅黑樹調整成目標的樣子。我們先把w的顏色置黑,因為它最終的顏色是黑色的,提前置黑能避免旋轉時的顏色交換。然后通過右旋z、左旋y把紅黑樹調整成目標形態(tài),然后把x的顏色置紅,然后再根據red_borrowed把x置黑。此種情況我們幫x借到了紅色,對應著2-3 B樹中借到了元素,所以循環(huán)結束。
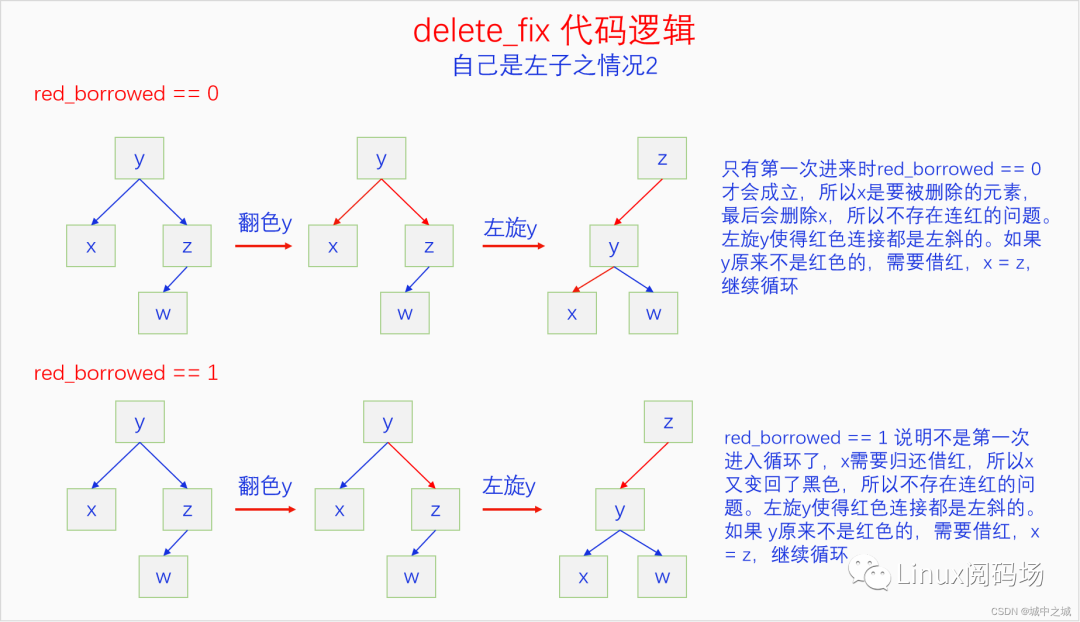
這種情況是兄弟節(jié)點沒法借的情況,只有向父節(jié)點借,向父節(jié)點借有兩種情況,一是父節(jié)點是紅色,能借到,循環(huán)就結束了,二是父節(jié)點是黑色,借不到,只能強行借了,把red_borrowed設置為1。我們還要考慮上一輪的red_borrowed,如果為1,要把借來的紅色還了,也就是說x剛借來紅色就還了,x還是黑色的。如果red_borrowed為0的話說明是第一次循環(huán),x是要被刪除的元素,所以不存在違背紅子不紅的問題。如果這一輪的red_borrowed是1的話則繼續(xù)循環(huán),否則就結束循環(huán)。
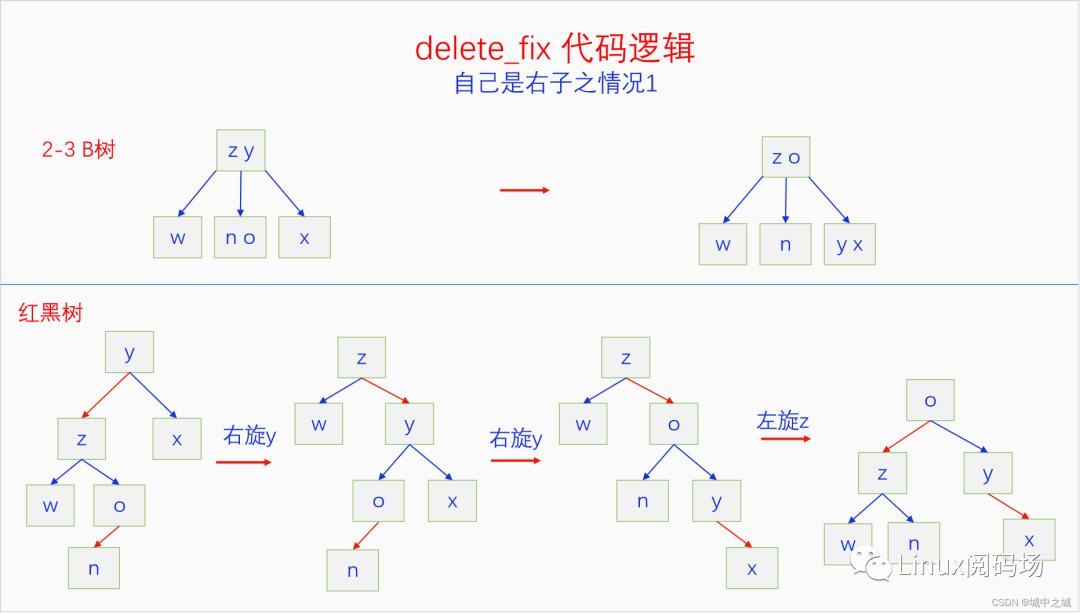
這是一種比較復雜的情況,對應著2-3 B樹的情況是父節(jié)點和兄弟節(jié)點都有兩個元素的情況。看紅黑樹比較復雜,我們看2-3 B樹是怎么操作的,通過B樹的操作反推紅黑樹應該如何操作。第一步我們右旋y,得到了一個x y o n ,一個局部有紅色節(jié)點的樹。第二步,只考慮這個樹,我們最后可以通過右旋y并調整顏色的方式把紅色轉移給x,這樣我們就達到目的了。然后我們發(fā)現o的顏色是右斜的,對z左旋一下,把它調整為一個左斜紅黑樹。
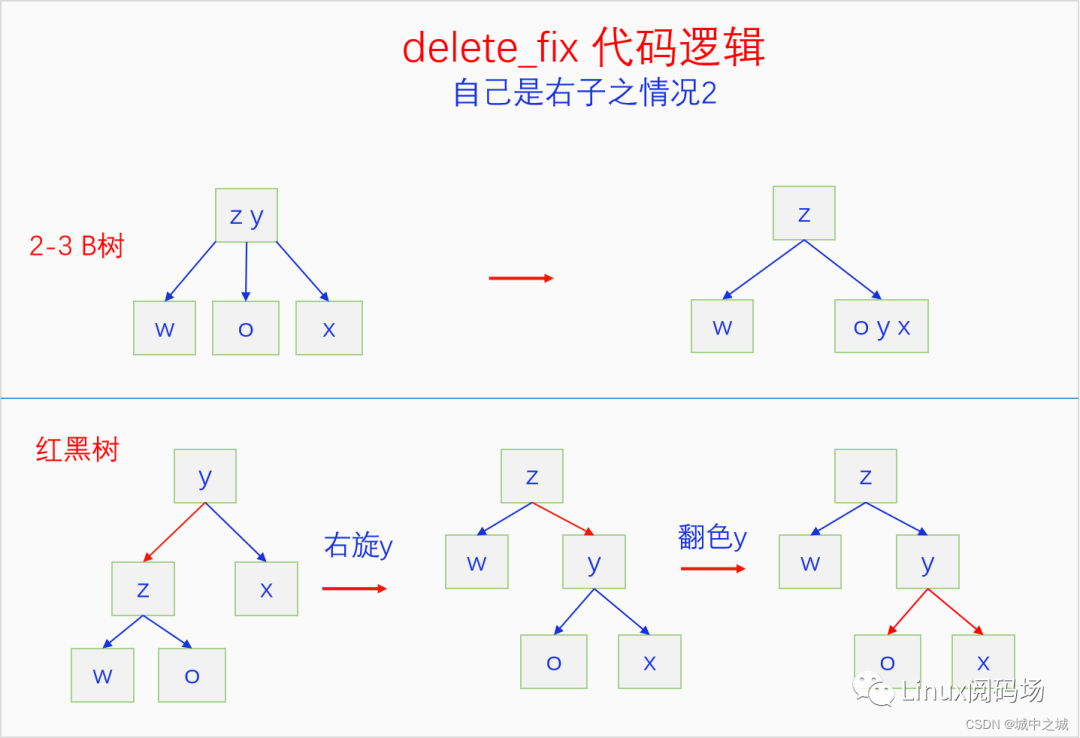
這種情況對應的2-3 B樹是父節(jié)點有兩個元素,向父節(jié)點借一個元素并和兄弟節(jié)點合并,所以我們先右旋y,然后對y進行翻色,x就變?yōu)榧t色了。通過前面的分析我們知道,雖然x是紅色右斜的,但是有兩種情況,要么x是被借紅的,所以還會變成黑色,要么x就是要被刪除的節(jié)點,所以不需要把x旋轉為左斜的。
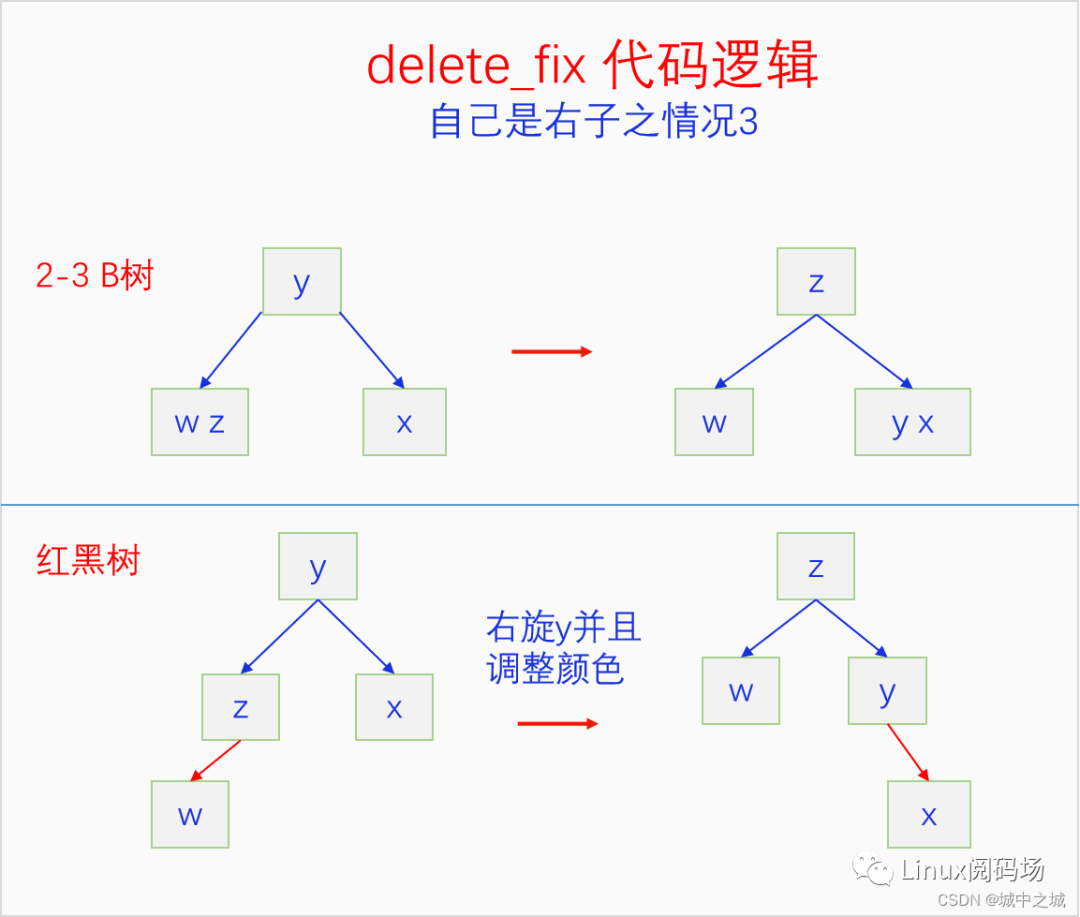
這種情況是父節(jié)點只有一個元素兄弟節(jié)點有兩個元素,直接向兄弟借元素,一個右旋y并調整顏色,就搞定了。
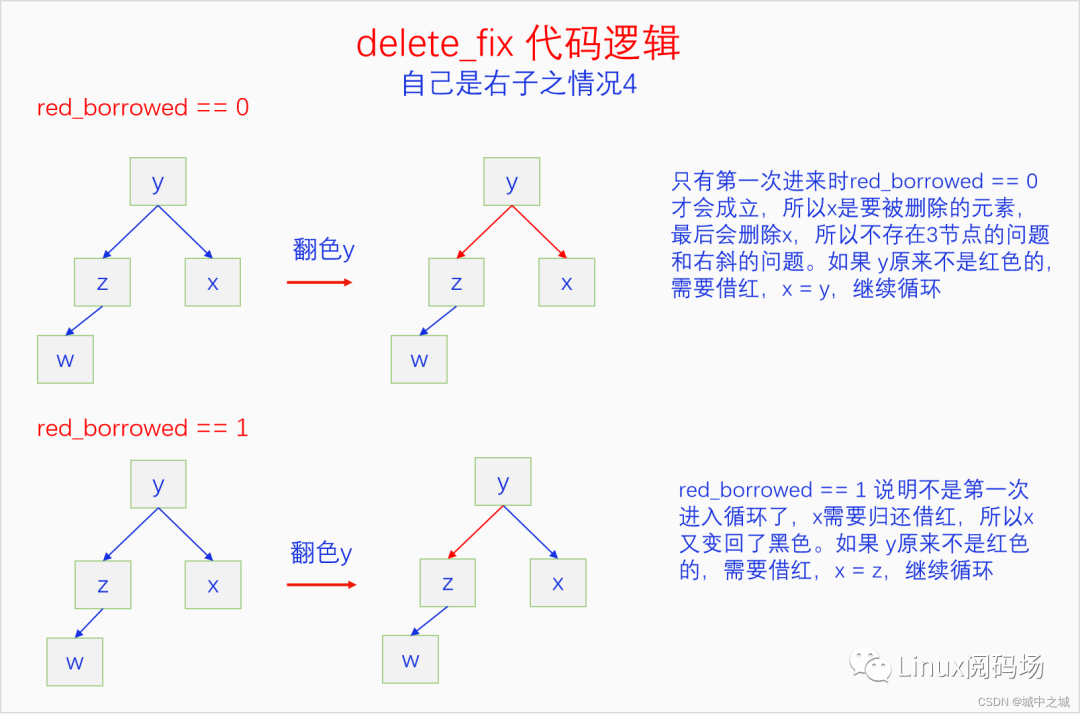
這種情況和左2是相同的,而且還比左2簡單,由于z是左斜的,所以旋轉的動作都省了。
五、總結回顧
紅黑樹是二叉樹和2-3 B樹結合而成的一種數據結構,理解紅黑樹的關鍵在于理解B樹的操作邏輯,理解了B樹就基本理解紅黑樹,紅黑樹的難點在于3元素節(jié)點的旋轉和翻色操作。本文先論述了紅黑樹和2-3 B樹之間的關系,然后用畫圖的方式詳細講解了2-3 B樹的操作邏輯,接著又用畫圖的方式了講解了紅黑樹是如何模擬2-3 B樹的操作邏輯的,最后用C語言實現了一個左斜紅黑樹。
審核編輯:劉清
-
存儲
+關注
關注
13文章
4320瀏覽量
85897 -
C語言
+關注
關注
180文章
7605瀏覽量
136990 -
二叉樹
+關注
關注
0文章
74瀏覽量
12338
原文標題:深入理解紅黑樹
文章出處:【微信號:LinuxDev,微信公眾號:Linux閱碼場】歡迎添加關注!文章轉載請注明出處。
發(fā)布評論請先 登錄
相關推薦
9.9萬元行業(yè)最低售價!宇樹智能人形機器人G1發(fā)布:“每天都在升級進化”

一千余字解讀stm32時鐘樹

請問PCM1864的驅動在設備樹該如何描述?
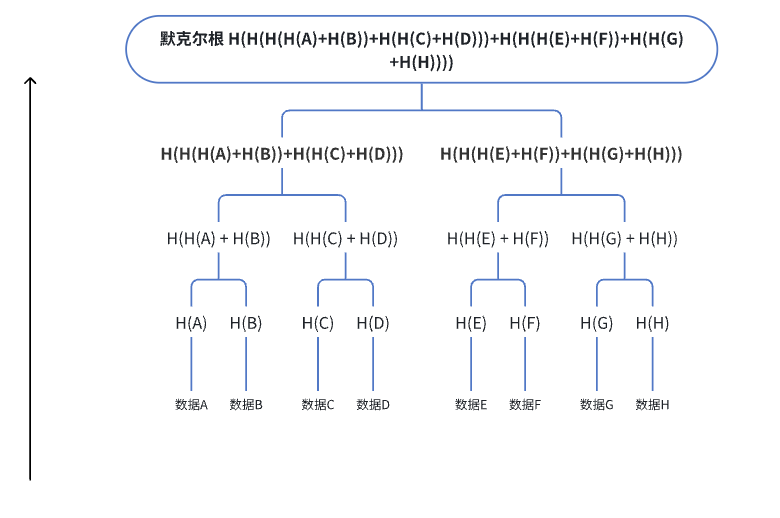
什么是默克爾樹(Merkle Tree)?如何計算默克爾根?
如何配置Linux操作系統(tǒng)設備樹讓我的開發(fā)板可以將板子上的GPIO接口用作 I2S輸出??
鴻蒙語言基礎類庫:ohos.util.HashMap 非線性容器HashMap

如何使用CubeMX生成的設備樹編譯鏡像?
原理圖設計里兩顆重要的樹(國產EDA)
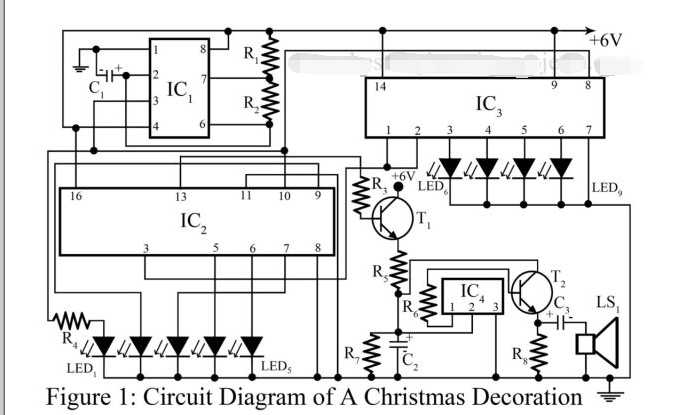
圣誕樹燈電路圖分享
OpenHarmony語言基礎類庫【@ohos.util.HashMap (非線性容器HashMap)】




 紅黑樹是如何模擬2-3 B樹的操作邏輯的
紅黑樹是如何模擬2-3 B樹的操作邏輯的










評論