圖解：卷積神經網絡數學原理解析

源自：數學中國

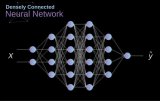
過去我們已經知道被稱為緊密連接的神經網絡。這些網絡的神經元被分成若干組，形成連續的層。每一個這樣的神經元都與相鄰層的每一個神經元相連。下圖顯示了這種體系結構的一個示例。

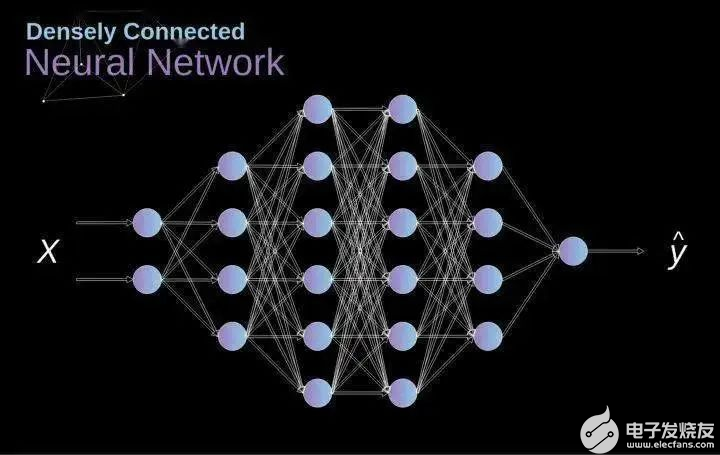
圖1. 密集連接的神經網絡結構

當我們根據一組有限的人工設計的特征來解決分類問題時，這種方法很有效。例如，我們根據足球運動員在比賽期間的統計數據來預測他的位置。然而，當處理照片時，情況變得更加復雜。當然，我們可以將每個像素的像素值作為單獨的特征，并將其作為輸入傳遞給我們的密集網絡。不幸的是，為了讓該網絡適用于一張特定的智能手機照片，我們的網絡必須包含數千萬甚至數億個神經元。另一方面，我們可以縮小我們的照片，但在這個過程中，我們會丟失一些有用的信息。我們立馬意識到傳統的策略對我們沒有任何作用，我們需要一個新的有效的方法，以充分利用盡可能多的數據，但同時減少必要的計算和參數量。這就是CNNs發揮作用的時候了。

數字圖像的數據結構

讓我們先花一些時間來解釋數字圖像是如何存儲的。你們大多數人可能知道它們實際上是由很多數字組成的矩陣。每一個這樣的數字對應一個像素的亮度。在RGB模型中，彩色圖像實際上是由三個對應于紅、綠、藍三種顏色通道的矩陣組成的。在黑白圖像中，我們只需要一個矩陣。每個矩陣都存儲0到255之間的值。這個范圍是存儲圖像信息的效率(256之內的值正好可以用一個字節表達)和人眼的敏感度(我們區分有限數量的相同顏色灰度值)之間的折衷。

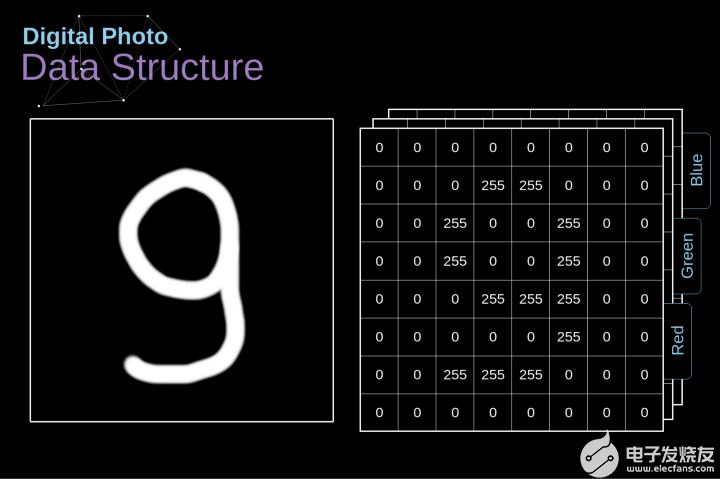
圖2. 數字圖像的數據結構

卷 積

核卷積不僅用于神經網絡，而且是許多其他計算機視覺算法的關鍵一環。在這個過程中，我們采用一個形狀較小的矩陣(稱為核或濾波器)，我們輸入圖像，并根據濾波器的值變換圖像。后續的特征map值根據下式來計算，其中輸入圖像用f表示，我們的kernel用h表示，結果矩陣的行和列的索引分別用m和n表示。

圖3. 核卷積的例子

將過濾器放置在選定的像素上之后，我們從kernel中提取每個相應位置的值，并將它們與圖像中相應的值成對相乘。最后，我們總結了所有內容，并將結果放在輸出特性圖的對應位置。上面我們可以看到這樣的操作在細節上是怎么實現的，但是更讓人關注的是，我們通過在一個完整的圖像上執行核卷積可以實現什么應用。圖4顯示了幾種不同濾波器的卷積結果。

圖4. 通過核卷積得到邊緣[原圖像

有效卷積和相同卷積

如圖3所示，當我們用3x3核對6x6的圖像進行卷積時，我們得到了4x4特征圖。這是因為只有16個不同的位置可以讓我們把濾波器放在這個圖片里。因為每次卷積操作，圖像都會縮小，所以我們只能做有限次數的卷積，直到圖像完全消失。更重要的是，如果我們觀察卷積核如何在圖像中移動，我們會發現位于圖像邊緣的像素的影響要比位于圖像中心的像素小得多。這樣我們就丟失了圖片中包含的一些信息。通過下圖，您可以知道像素的位置如何改變其對特征圖的影響。

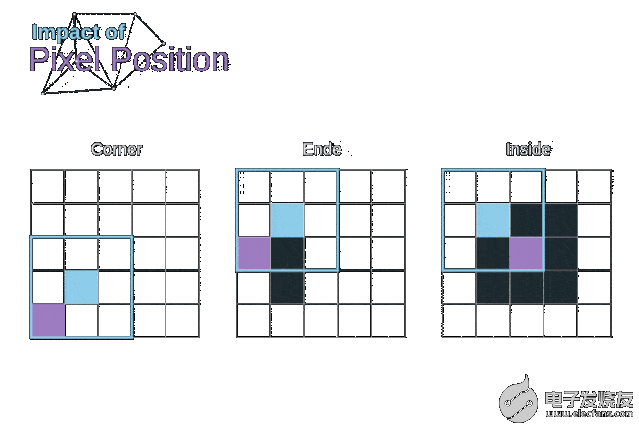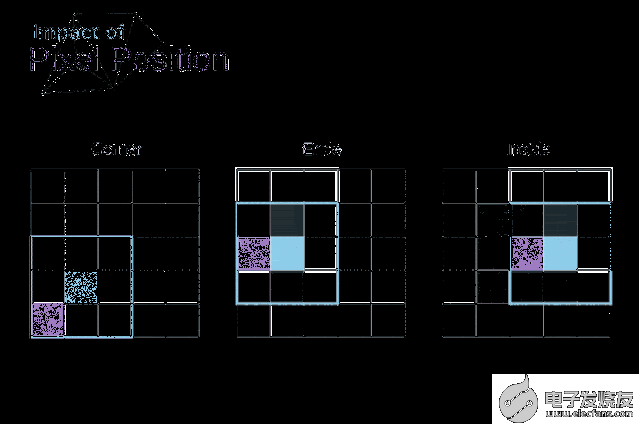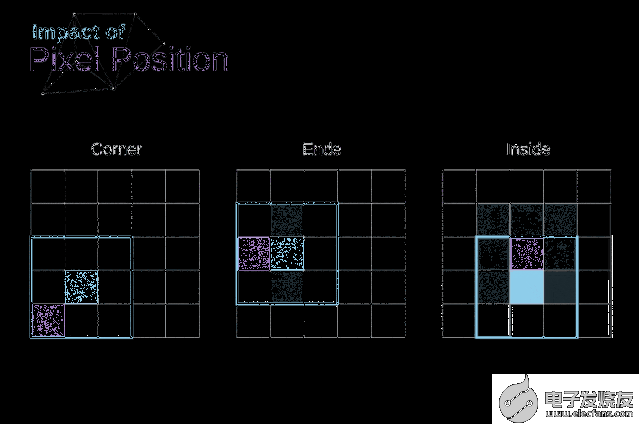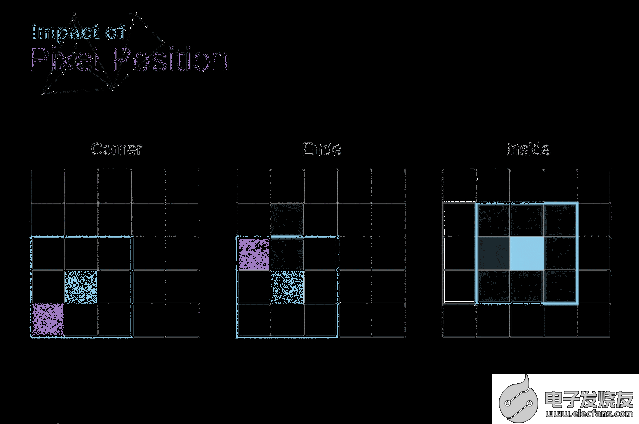
圖5. 像素位置的影響

為了解決這兩個問題，我們可以用額外的邊框填充圖像。例如，如果我們使用1px填充，我們將照片的大小增加到8x8，那么與3x3濾波器卷積的輸出將是6x6。在實踐中，我們一般用0填充額外的填充區域。這取決于我們是否使用填充，我們要根據兩種卷積來判斷-有效卷積和相同卷積。這樣命名并不是很合適，所以為了清晰起見:Valid表示我們僅使用原始圖像，Same表示我們同時也考慮原圖像的周圍邊框，這樣輸入和輸出的圖像大小是相同的。在第二種情況下，填充寬度應該滿足以下方程，其中p為填充寬度和f是濾波器維度(一般為奇數)。

步幅卷積

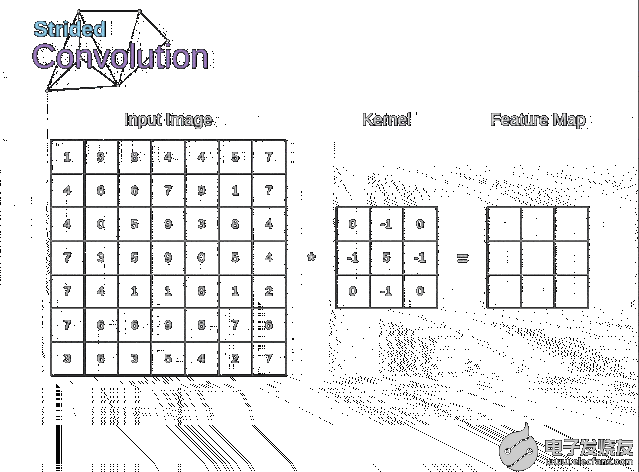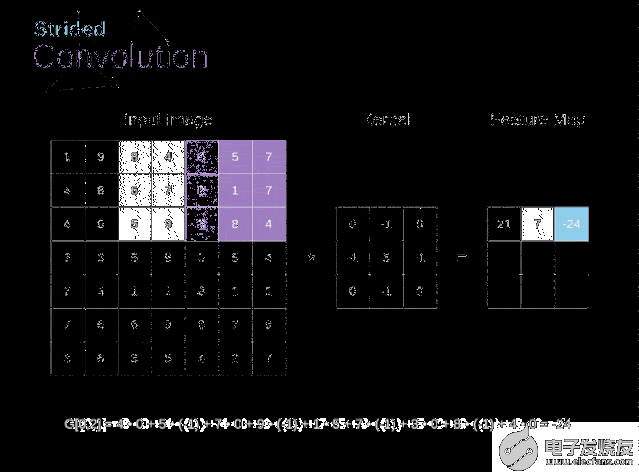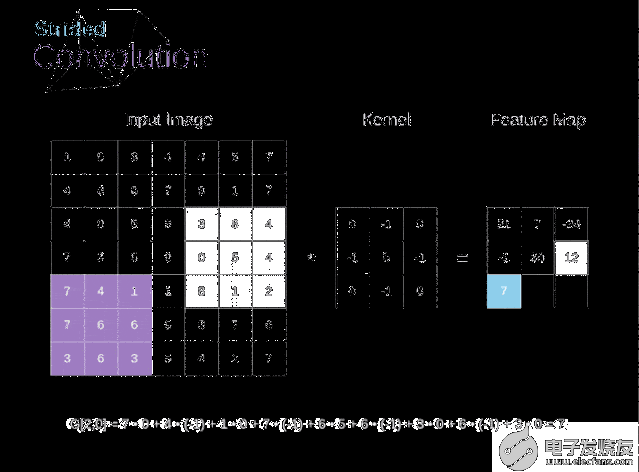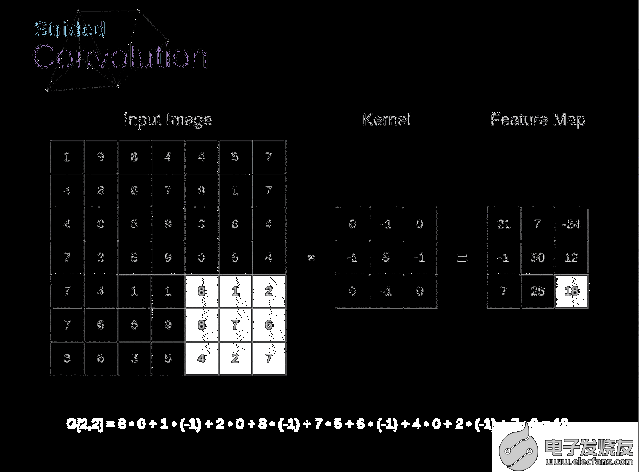
圖6. 步幅卷積的例子

在前面的例子中，我們總是將卷積核每次移動一個像素。但是，步幅也可以看作卷積層超參數之一。在圖6中，我們可以看到，如果我們使用更大的步幅，卷積看起來是什么樣的。在設計CNN架構時，如果希望感知區域的重疊更少，或者希望feature map的空間維度更小，我們可以決定增加步幅。輸出矩陣的尺寸——考慮到填充寬度和步幅——可以使用以下公式計算。

過渡到三維

空間卷積是一個非常重要的概念，它不僅能讓我們處理彩色圖像，更重要的是在單層中應用多個卷積核。第一個重要的原則是，過濾器和要應用它的圖像必須具有相同通道數。基本上，這種方式與圖3中的示例非常相似，不過這次我們將三維空間中的值與卷積核對應相乘。如果我們想在同一幅圖像上使用多個濾波器，我們分別對它們進行卷積，將結果一個疊在一起，并將它們組合成一個整體。接收張量的維數(即我們的三維矩陣)滿足如下方程:n-圖像大小，f-濾波器大小，nc-圖像中通道數，p-是否使用填充，s-使用的步幅，nf-濾波器個數。

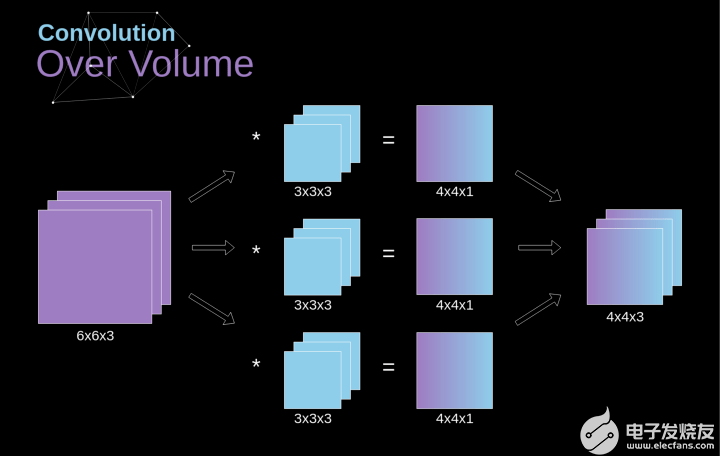
圖7. 三維卷積

卷積層

現在是時候運用我們今天所學的知識來構建我們的CNN層了。我們的方法和我們在密集連接的神經網絡中使用的方法幾乎是一樣的，唯一的不同是這次我們將使用卷積而不是簡單的矩陣乘法。正向傳播包括兩個步驟。第一步是計算中間值Z,這是利用輸入數據和上一層權重W張量(包括所有濾波器)獲得的卷積的結果,然后加上偏置b。第二步是將非線性激活函數的應用到獲得的中間值上(我們的激活函數表示為g)。對矩陣方程感興趣的讀者可以在下面找到對應的數學公式。如果您不清楚其中的操作細節，我強烈推薦我的前一篇文章，在那篇文章中，我詳細討論了緊密連接的神經網絡的原理。順便說一下，在下圖中你可以看到一個簡單的可視化，描述了方程中使用的張量的維數。

連接剪枝和參數共享

在文章的開頭，我提到密集連接的神經網絡不擅長處理圖像，這是因為需要學習大量的參數。既然我們已經理解了卷積是什么，讓我們現在考慮一下它是如何優化計算的。在下面的圖中，以稍微不同的方式顯示了二維卷積，以數字1-9標記的神經元組成了輸入層，并接受圖像像素亮度值，而A - D單元表示計算出的特征map元素。最后，I-IV是需要經過學習的卷積核的值。

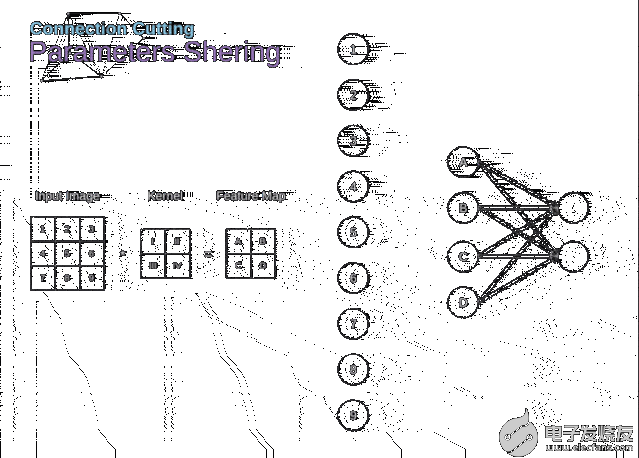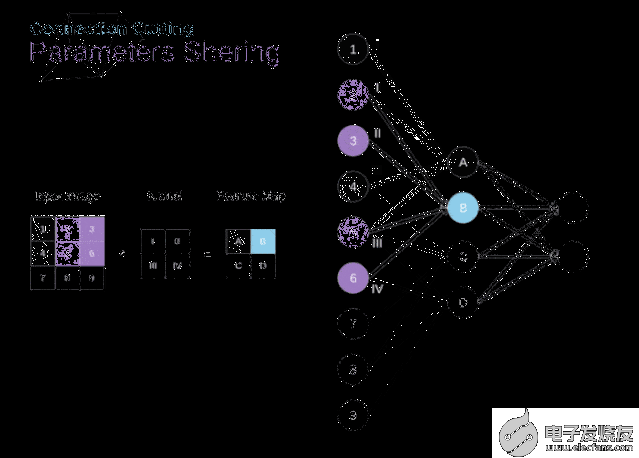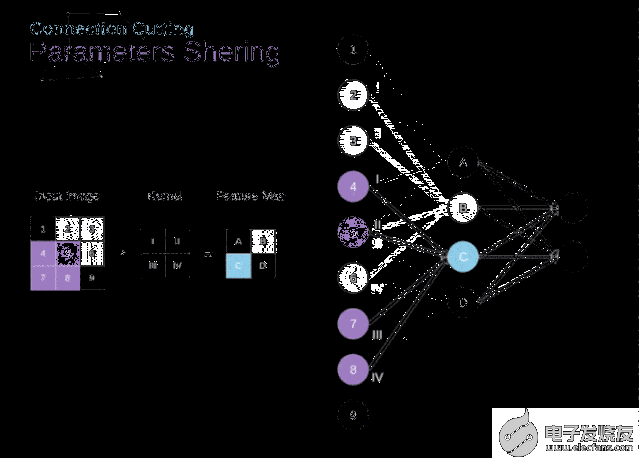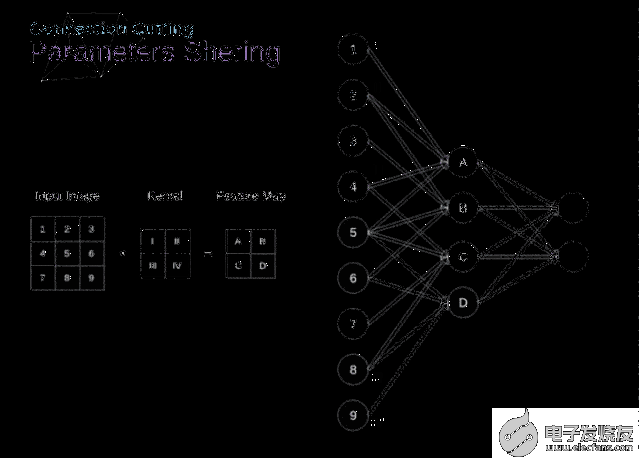
圖9. 連接剪枝和參數共享

現在，讓我們關注卷積層的兩個非常重要的屬性。首先，你可以看到，并不是所有連續兩層的神經元都相互連接。例如，神經元1只影響A的值。其次，我們看到一些神經元共享相同的權重。這兩個性質都意味著我們需要學習的參數要少得多。順便說一下，值得注意的是，濾波器中的一個值會影響特征map中的每個元素——這在反向傳播過程中非常重要。

卷積層反向傳播

任何嘗試過從頭編寫自己的神經網絡代碼的人都知道，完成正向傳播還沒有完成整個算法流程的一半。真正的樂趣在于你想要進行反向傳播得到時候。現在，我們不需要為反向傳播這個問題所困擾，我們可以利用深度學習框架來實現這一部分，但是我覺得了解底層是有價值的。就像在密集連接的神經網絡中，我們的目標是計算導數，然后用它們來更新我們的參數值，這個過程叫做梯度下降。

在我們的計算中需要用到鏈式法則——我在前面的文章中提到過。我們想評估參數的變化對最終特征map的影響，以及之后對最終結果的影響。在我們開始討論細節之前，讓我們就對使用的數學符號進行統一——為了讓過程更加簡化，我將放棄偏導的完整符號，而使用如下所示的更簡短的符號來表達。但記住，當我用這個符號時，我總是指的是損失函數的偏導數。

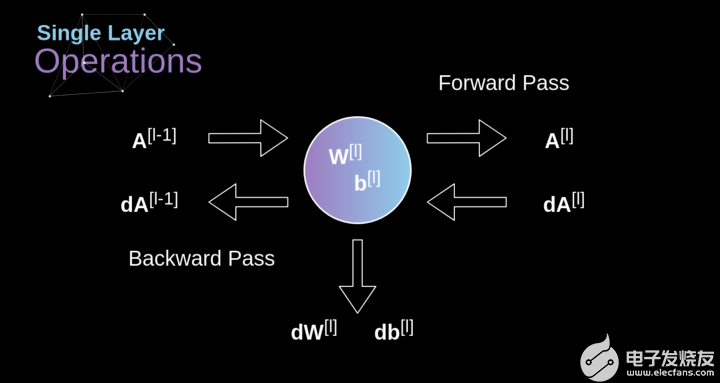
圖10. 單卷積層的輸入和輸出的正向和反向傳播

我們的任務是計算dW[l]和db[l]——它們是與當前層參數相關的導數，以及dA[l -1]的值——它們將被傳遞到上一層。如圖10所示，我們接收dA[l]作為輸入。當然，張量dW和W、db和b以及dA和A的維數是相同的。第一步是通過對輸入張量的激活函數求導得到中間值dZ[l]。根據鏈式法則，后面將使用這個操作得到的結果。

現在，我們需要處理卷積本身的反向傳播，為了實現這個目的，我們將使用一個矩陣運算，稱為全卷積，如下圖所示。注意，在這個過程中，對于我們使用卷積核，之前我們將其旋轉了180度。這個操作可以用下面的公式來描述，其中濾波器用W表示，dZ[m,n]是一個標量，屬于上一層偏導數。

圖11. 全卷積

池化層

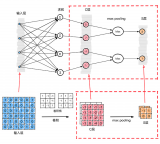
除了卷積層，CNNs還經常使用所謂的池化層。池化層主要用于減小張量的大小和加速計算。這種網絡層很簡單——我們需要將圖像分割成不同的區域，然后對每個部分執行一些操作。例如，對于最大值池化層，我們從每個區域中選擇一個最大值，并將其放在輸出中相應的位置。在卷積層的情況下，我們有兩個超參數——濾波器大小和步長。最后一個比較重要的一點是，如果要為多通道圖像進行池化操作，則應該分別對每個通道進行池化。

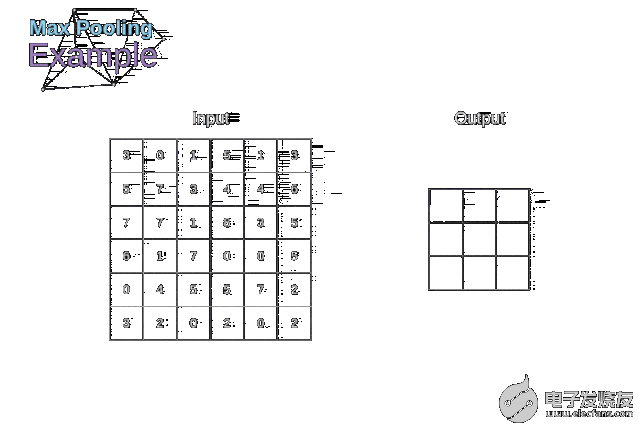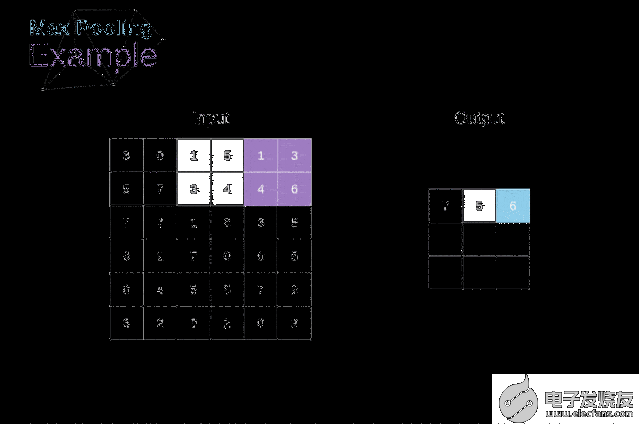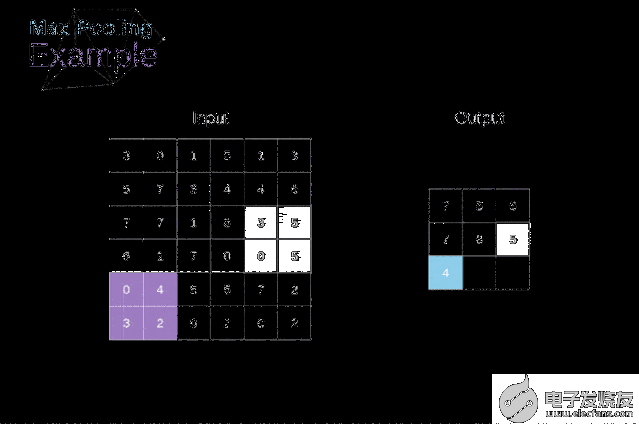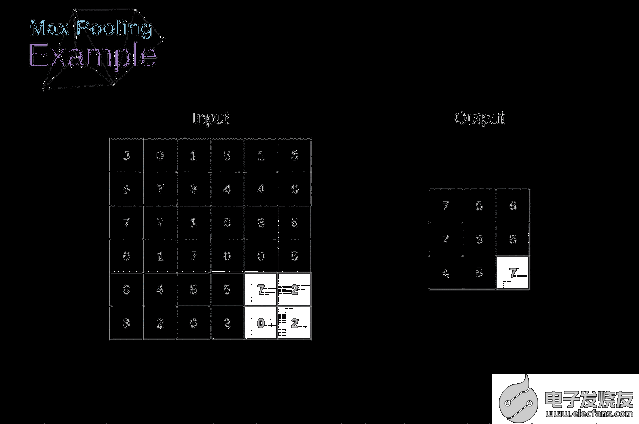
圖12. 最大值池化的例子

池化層反向傳播

在本文中，我們將只討論最大值池化的反向傳播，但是我們將學習的規則只需要稍加調整就可以適用于所有類型的池化層。由于在這種類型的層中，我們沒有任何必須更新的參數，所以我們的任務只是適當地分布梯度。正如我們所記得的，在最大值池化的正向傳播中，我們從每個區域中選擇最大值，并將它們傳輸到下一層。因此，很明顯，在反向傳播過程中，梯度不應該影響矩陣中沒有包含在正向傳播中的元素。實際上，這是通過創建一個掩碼來實現的，該掩碼可以記住第一階段中使用的值的位置，稍后我們可以使用該掩碼來傳播梯度。

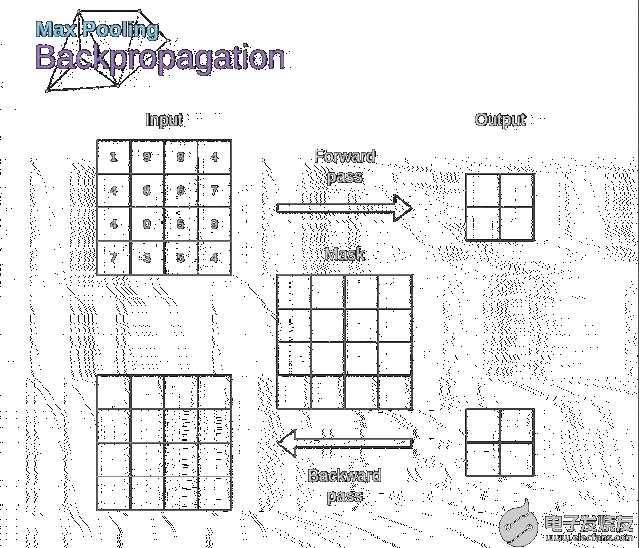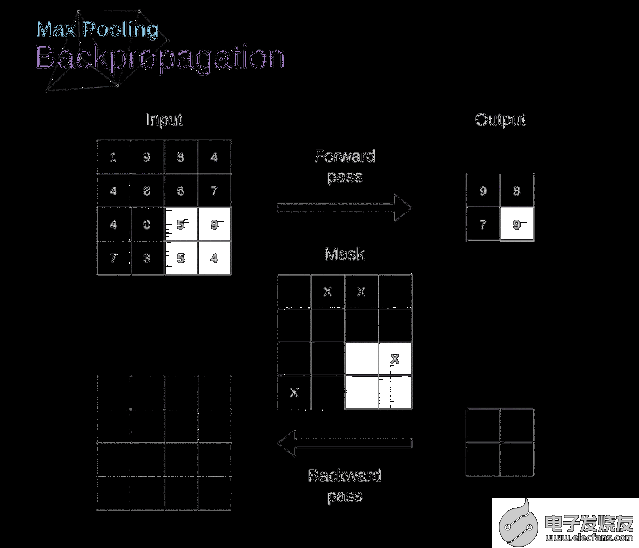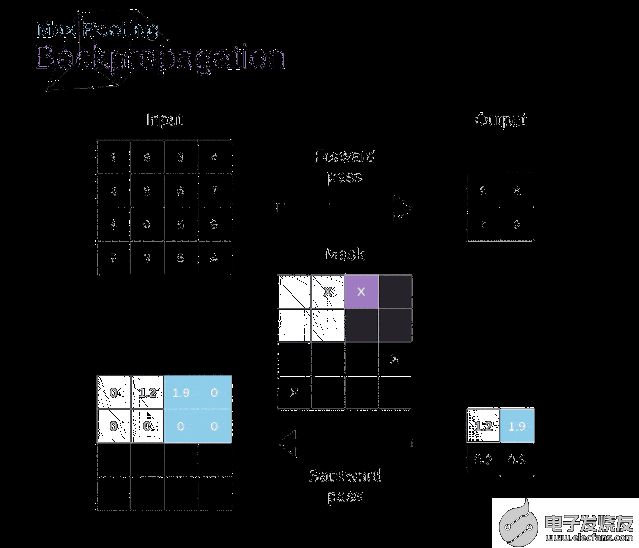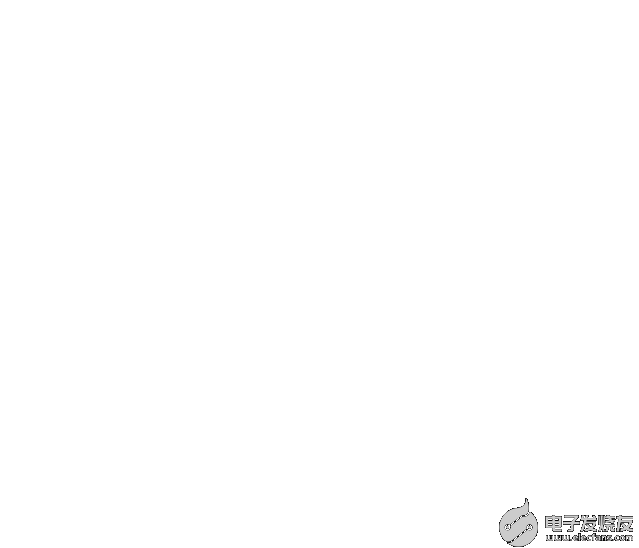
圖13. 最大值池化的反向傳播

審核編輯 黃昊宇