在中學物理中,我們就接觸過動量(Momentum)這一概念。一個運動物體所具有的動量等于該物體的質量乘以它的速度。當兩個物體發生彈性碰撞時,動量可以在二者之間轉移。比如在打臺球時,用白色主球撞擊其他球的過程,也就是將白色主球的部分或者全部動量轉移給其他球的過程。
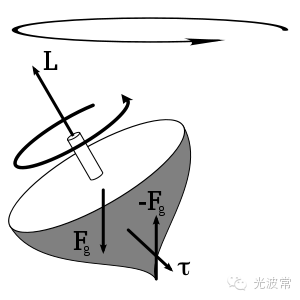
當一個物體圍繞著某個軸轉動時,該物體還具有角動量(Angular momentum)。角動量的大小正比于物體的質量、轉動的速度以及物體到軸的距離;角動量是個矢量,其方向垂直于物體轉動的平面。在沒有外加力矩(或者總體外加力矩為零)的情況下,物體的角動量大小和方向保持不變。利用了角動量大小守恒這一原理,花樣滑冰選手在做旋轉動作時,可以將雙臂抱緊以減小身體到旋轉軸的有效距離從而增加旋轉速度。角動量方向守恒在日常生活中更是有諸多應用,比如陀螺在高速旋轉時能直立在地面上,子彈必須高速旋轉才能準確擊中目標,美式橄欖球傳球時讓球旋轉等等。為了與角動量區分,在前面提到的、由質量與速度乘積定義的動量又被稱為線性動量(Linear Momentum)。
(from wiki)
其實光也具有這三種動量:線性動量、自旋角動量和軌道角動量。如果一個兵乓球撞到鏡子上,被彈開,由于線性動量的改變(主要是方向)導致在彈開瞬間對鏡面產生壓力。類似的,當照射在鏡面上的光被鏡子反射時,光的線性動量發生改變,從而對鏡子產生一個壓力(推力),這種壓力也被稱為輻射壓力(Radiation pressure)。
光對被照射的物體施加輻射壓力這一概念,最早由德國數學家和天文學家開普勒在1619年提出。當時人們發現彗星接近太陽時,總是拖著長長的尾巴(彗尾),而且尾巴總是出現在彗星背向太陽的一側。開普勒認為是太陽光的輻射壓力將彗星中很多塵埃顆粒推向彗星身后,從而在其背向太陽的一側形成彗尾。
在中國傳統文化中,彗星象征著不吉利。又因為看起來像個掃把,所以彗星在中國又被稱為掃把星。哈雷彗星每76年光臨一次地球。世界上公認的對哈雷彗星最早的記錄,來源于《史記》。
1871年,電磁學集大成者麥克斯韋在理論上預言了輻射壓力現象。輻射壓力很小,將平均功率為5毫瓦的激光垂直入射到鏡子表面,假定所有光被反射,那么鏡面所感受到的壓力只有33×10-12牛頓。毫無疑問,在200多年前測量如此小的力,是一件極具挑戰性的工作。好在當時物理學界已經普遍采用扭秤(Torsion
balance)測量微小的力。這種方法最早由法國物理學家庫侖在1777年發明。為了測量電荷之間的靜電引力或斥力,庫侖將一個絕緣橫桿用細絲水平懸在空中,絕緣橫桿的一端裝有一個帶電小球。由于電荷間引力或者斥力的作用,當另外一個帶電小球在水平方向上靠近橫桿末端的小球時,絕緣橫桿會發生轉動,轉動的角度取決于力的大小。利用扭秤,庫侖發現了著名的庫侖定律:兩個點電荷之間的作用力正比于二者電量乘積,反比于二者間距離的平方。1798年,英國科學家卡文迪許利用扭秤間接測量了萬有引力常數(Gravitationa
constant)。
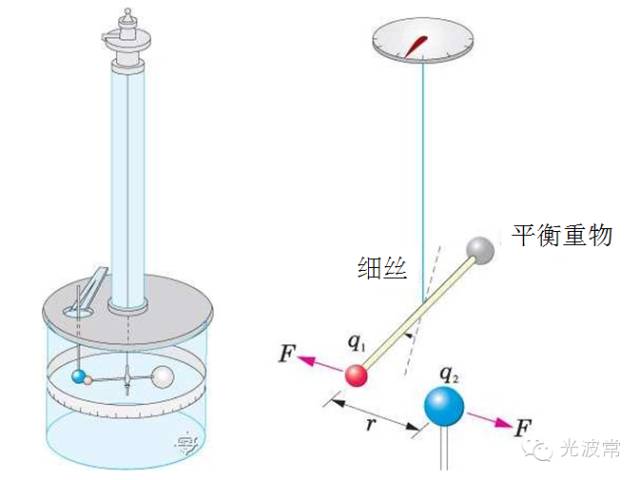
庫侖扭秤 (Adapted from Wiki)
扭秤將力的測量轉化為細絲扭轉角度的測量。顯然,這種方法的測量精度和靈敏度由細絲的力學性質決定,當時常用的材料包括頭發、絲綢或者鎢絲等等。英國實驗物理學家Charles Vernon Boys,一直癡迷于建造能用于精確測量的各種實驗裝置。為了進一步改進扭秤,Boys測試了很多材料后想到了玻璃纖維(Glass fiber)。玻璃纖維的出現可以追溯到公元前1600年的埃及。到19世紀晚期,上好的玻璃纖維可以比蠶絲還要纖細,那時人們經常把不同顏色的玻璃纖維編織成布匹,用以各種裝飾。1887年,Boys能找到的玻璃纖維最小直徑為25微米,測試效果并不理想,表明需要采用更細的玻璃纖維。
當時獲得玻璃纖維的辦法,是將熔化后的細玻璃棒快速拉成細絲。因此要想獲得更細的玻璃纖維,就要想辦法提高在玻璃熔化后拉纖維的速度。為此,Boys制作了一把弩,然后將質量很輕的箭裝在弩上,再將玻璃預制棒的一端固定在箭尾上。等預制棒被加熱到1600攝氏度熔化后,箭被弩快速射出,后面就能拖出長長的玻璃纖維。利用這種辦法,Boys可以輕松獲得27米長、直徑在2.5微米的玻璃纖維。借助石英(Quartz)玻璃纖維,Boys研制成輻射微熱計(Radio micrometer),能夠測量到放在5公里之外的點燃的蠟燭所產生的熱效應。
自此石英玻璃纖維成為制作扭秤裝置的不二之選。利用這種扭秤,在1900年俄羅斯物理學家PyotrLebedev實驗驗證了由于光線性動量的改變而產生的輻射壓力。
如果將光束聚焦,在焦點附近的物體的不同部分感受到來自不同方向上的光線,這些光線在物體表面既有反射又有折射,反射和折射改變光的線性動量,因此光對物體產生力的作用,由于光強在焦點附近是梯度分布從而對物體產生了梯度力(Gradient force)。如果物體很小(納米到微米量級)很輕,它會被聚焦光束限制在焦點附近、合力為零的平衡位置。通過移動光束的焦點位置,被“抓住”的微小物體也會隨之被移動。這種技術稱為光鑷子,最早于1970年由在貝爾實驗室工作的Ashkin發明,隨即被廣泛應用于生物學研究,用于操作生物大分子或者細胞等。
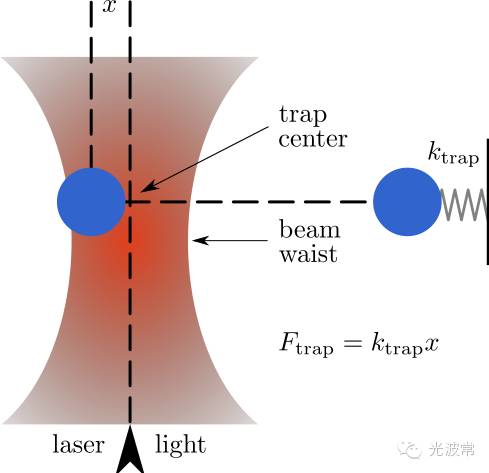
(from Wiki)
在用量子力學描述的世界中,物理學家用光子(Photon)來描述光和其他基本粒子的相互作用。對于一個光子,它的線性動量為普朗克常數除以波長。
光子當然也有自旋角動量。1909年,光子的概念尚未建立之前,英國物理學家John Poynting就提出圓偏振光具有角動量(實際上是自旋角動量),并且認為當光經過某個光學器件(比如波片)改變偏振態時,會伴隨著角動量在光和器件之間的轉移。1936年,Beth將一個半波片水平懸掛在石英玻璃纖維上制成扭秤,當右旋圓偏振光通過該波片轉換為左旋圓偏振光時,光束自旋角動量的改變引起了波片轉動。
該實驗的測量結果驗證了Poynting的猜想。現在我們知道,左(右)旋圓偏振的光子具有的自旋角動量為正(負)的普朗克常數除以2倍的圓周率。一個線偏振光,可以分解為幅度相等的兩個旋轉方向相反的圓偏振光的線性疊加,因此它的自旋角動量為零。
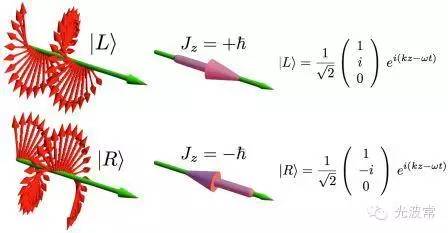
(Adapted from Wiki)
令人吃驚的是,直到1992年,物理學家們才意識到光也可以具有軌道角動量。眾所周知,我們熟悉的高斯光束是旁軸波動方程(Paraxial wave equation)的厄米-高斯(Hermite-Gaussian)本征解中的最低階模式HG00。其實旁軸波動方程還有另外一組完備的正交本征解,那就是不太被大家熟知的拉蓋爾-高斯(Laguerre-Gaussian)模式,通常記為LG(p,n)。p和n分別取0,1,2,...整數,用來表示不同階的模式,比如LG(0,0)對應的就是我們常見的高斯光束。對于n不為0的高階拉蓋爾-高斯光束,在光束的中心,光強為零,同時該光束的波前(Wave front)為螺旋狀(Hellical),表征光束能量傳輸的Poynting矢量也沿著螺旋曲線(Spiral trajectory)前行。
1986年,Coullet意識到在數學上,這種具有螺旋波前的拉蓋爾-高斯光束與流體力學中的渦旋具有相似之處,因此將前者命名為光渦旋(Optical votex)。1992年,荷蘭萊頓大學的Allen等人意識到光渦旋攜帶有另外一種角動量--軌道角動量。對于模式為LG(p,n)的拉蓋爾-高斯光束來說,其中每個光子具有的軌道角動量為n乘以普朗克常數除以兩倍的圓周率。
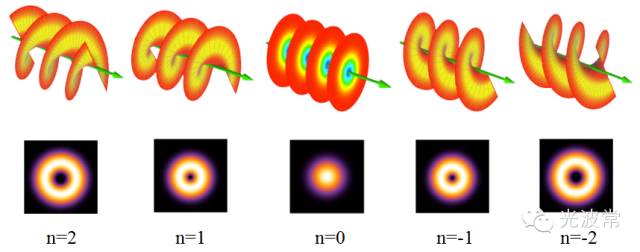
高階拉蓋爾-高斯光束的螺旋波前和光強分布
近年來,研究和利用光束的角動量儼然成為光學前沿之一。比如,利用圓偏振的高斯光束聚焦形成的光鑷子不僅可以“抓住”微小物體,并且可以將光束本身的自旋角動量轉移到微小物體上,從而對微小物體進行轉動操作--有人將這樣的光學裝置形象地稱為光扳手(Optical spanner)。類似的光扳手也可以通過聚焦線性偏振的(自旋角動量為0)、n不為0的高階拉蓋爾-高斯光束來實現,只不過依靠的是光束本身的軌道角動量來轉動微小物體。
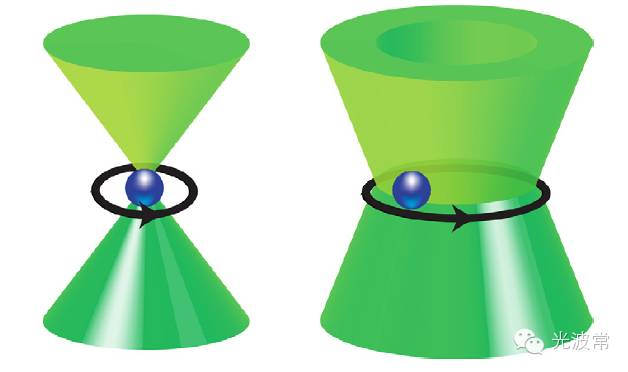
(Adapted from A.M. Yao and M. J. Padgett, “Orbital angularmomentum: origins, behavior and applications,” Advancesin Optics and Photonics 3, 161 (2011).)
審核編輯:劉清
-
電荷
+關注
關注
1文章
631瀏覽量
36152 -
電磁學
+關注
關注
1文章
106瀏覽量
14192
原文標題:光的動量——從光鑷子到光扳手
文章出處:【微信號:bdtdsj,微信公眾號:中科院半導體所】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
基本放大電路有哪三種
mosfet的三種工作狀態及工作條件是什么
單片機的三種總線結構
vim的三種工作模式有哪些
放大電路的三種組態可以放大什么
晶體管的三種工作狀態
三種實現光模塊更高傳輸速率的技術
運放的三種應用
示波器的三種觸發模式





 淺析光具有的三種動量
淺析光具有的三種動量










評論