與電容器和電阻器一樣,電感器也是無源元件。簡單地說,電感器是導電材料的絞合線或線圈。電感是電導體或電路的特性,它反對電流的變化。
簡單來說,具有電感特性的電導體或電路元件稱為電感器。當線圈或絞合線(電感器)中的電流發生變化時,它會通過在自身和附近的導電材料中產生或感應電動勢 (EMF) 來對抗這種變化。
電感器以磁場的形式存儲能量。由于磁場與電流有關,電感與載流材料有關。塑料、木材和玻璃等介電材料的電感最小。但鐵磁性物質(鐵、鋁鎳鈷、三氧化二鉻)會有很高的電感。
線圈中的電感主要兩種類型,它們是自感和互感。那么,自感和互感的有什么區別,其計算公式又是什么?下面分別來介紹下。
自感
自感是載流導體的特性,當電流發生變化時,其中會感應出EMF。
當交流變化的電流流過電感線圈時,線圈中的磁通量也會發生變化,從而產生感應電動勢。這個過程稱為“自感”,線圈實現的電感稱為“自感”。
自感的概念可以通過假設載流電路元件或N匝電感線圈來理解,當電流流過線圈時,會在線圈內外產生磁場。由于該磁場而引入了磁通量。那么,線圈的自感就是每單位電流的磁鏈。當電感線圈與由電場引起的磁力線相交時,線圈本身就會產生自電動勢。
換句話說,自感是指線圈抵抗電流變化的能力。它以亨利為單位。線圈的磁性或磁性會影響線圈的自感。這就是為什么使用鐵磁材料通過增加線圈中的磁通量來增加線圈的電感的原因。
求線圈自感的表達式為:L = N Φ /I
其中N代表線圈的匝數,Φ是磁通量,I是由于產生的電動勢而產生的電流,L表示以亨利為單位的電感值。
自感電動勢和自感系數
我們知道流過電感的電流用I表示,Φ是磁通量,它們都彼此成正比,所以它可以表示為 I ∝ Φ。
電感器的匝數也與線圈中的電流成正比,所以可以推導出電流與其中感應的電動勢之間的關系為:(dΦ)/dt = L (di)/dt
電感值取決于線圈的幾何形狀或形狀,該值稱為“自感系數”。
e = – (dΦ)/dt
e = – L (di )/dt
我們可以根據需要設計電感線圈,使用高磁導率或低磁導率材料,并使用不同匝數的線圈。電感器鐵芯內部產生的磁通量為:Φ = B x A,這里B是磁通密度,A是線圈占據的面積。
示例1:長螺線管中的自感
如果考慮一個長的中空螺線管,其橫截面積為A,長度為l,匝數為n,則由于電流I的流動,其磁場為:B = μ0 H = μ0(NI )/l,螺線管中的總通量為 N Φ = LI。
將其代入上述等式,則有:L = N Φ /I ,L = (μ0 N 2 A )/ l
其中L是亨利的自感,μ0是空氣或中空空間的滲透率,N代表線圈即電感的匝數,A是螺線管的內橫截面積,l是線圈的長度且以米為單位。
以上就是長的空心螺線管的自感。μ表示填充螺線管的材料的絕對磁導率。在這種情況下,我們計算了空心螺線管的自感,因此使用μ0。為了獲得高磁導率或產生高磁通量,可以用軟鐵等鐵磁物質填充螺線管。
示例2:圓形線圈的自感
考慮一個橫截面積為A=π r2的圓形線圈,其中匝數為N。則磁通量為:B = μ0 (NI )/2r,圓形導體中的總通量為N Φ = LI。
將其代入上述等式,則有:
L = N Φ /I ,L = (μ_0 N 2 A )/2r
眾所周知,圓的面積是A = π r 2,所以圓形電感的自感也可以表示為:L = (μ0 N? 2 π r )/2
影響自感的因素
觀察上面的電感方程可以清楚的知道,共有4個因素會影響線圈的自感,它們是:
線圈匝數(N)
電感線圈面積 (A)
線圈長度 (l)
線圈材料
1、線圈匝數
線圈的電感取決于線圈的匝數,線圈中的匝數或捻數與電感成正比,即:N∝L。
所以,匝數越高意味著電感值越大,而減少匝數意味著降低電感值。
2、橫截面面積
線圈的電感會隨著電感器橫截面積的增加而增加,即:L∝N。如果線圈的面積大,它會產生更多的磁通量線,這導致形成更多的磁通量,因此電感會很高。
3、線圈長度
長線圈感應的磁通量小于短線圈感應的磁通量。隨著感應磁通量減少,線圈的電感也減少。所以線圈的感應與線圈的電感成反比,即:L∝ 1/l。
4、線圈材料
包裹線圈的材料的磁導率將對感應電動勢和電感產生影響。具有高磁導率的材料可以產生低電感,即:L∝μ0。
我們知道 μ = μ0 μr,所以 L∝ 1 / μr
互感
由于其耦合或相鄰線圈的電流變化而在線圈中感應電動勢的現象稱為“互感”,這里兩個線圈受到相同磁場的影響。由互感產生的電動勢可以用法拉第定律來解釋,而電動勢的方向可以用楞次定律來描述。
電動勢的方向總是與磁場的變化相反。第二個線圈中感應的電動勢是由于第一個線圈的電流變化引起的。第二個線圈中感應的電動勢可以表示為:
EMF2 = – N2 A ΔB/Δt = -M (ΔI1)/Δt
其中M是互感,它是第二個線圈中產生的電動勢與第一個線圈中的電流變化之間的比例。
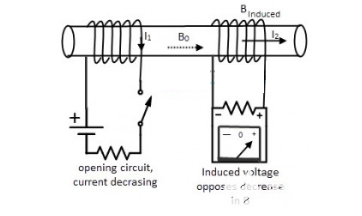
要了解互感的概念,可以觀看上圖。在連接的兩個電感器纏繞在單個導體上,假設它們為回路1和回路2。如果回路1中的電流發生變化,則感應出磁通量。當回路2截斷磁通量時,沒有任何電流直接流入第二個線圈,將產生一些感應電動勢,這種現象稱為“互感”。
互感電動勢和互感系數
每當將2個線圈保持在電流變化場中時,都會因為電流而感應出電動勢。隨著回路中的電流變化,磁通量也會變化。
在這種情況下,互感是一個矢量,因為它可能由于第一線圈中的電流而在第二線圈中感應,或者可能由于第二線圈產生的磁通量(B)而在第一線圈中感應。
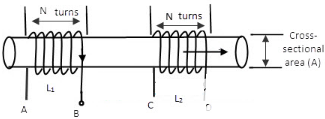
當電感器1中流動的電流發生變化時,會在其周圍產生磁通量(根據楞次定律和法拉第定律)。然后,由于第一個線圈中的電流,第二個線圈中的相互感應電動勢將被給出為:
M12 = (N2 Φ12)/I1
其中M12是線圈2中的互感,N是循環中的匝數,Φ12是線圈2中產生的磁通量,I1是回路1中的電流。
同樣,當我們改變電感器1中的電流時,會在其周圍產生磁通量。那么由于第2線圈中的電流而在第1線圈中產生的互感電動勢將給出為:
M21 = (N2 Φ21)/I2
其中M21是線圈1中的互感,N是循環中的匝數,Φ21是線圈1中產生的磁通量,I2是回路2中的電流。
需要記住的重要一點是,M21 = M12 = M,與兩個線圈的相對位置、大小和匝數無關。這稱為“互感系數”。
每個線圈的自感公式為:
L1 = (μ 0 μr N1 2 A)/l 和 L2 = (μ 0 μr N2 2 A)/l
從上面的等式,可以寫出 M2 = L1 L2。這是每個線圈的自感與互感之間的關系。當然,它也可以寫成M = √(L1 L2 ) Henry。
上式表示沒有磁通泄漏的理想條件,但實際上,由于線圈的位置和幾何形狀,總會存在一些磁漏。
磁耦合系數或耦合系數
兩個線圈之間的電感耦合量用“耦合系數”表示。耦合系數的值將小于1并始終大于0,即介于0和1之間,用“k”表示。
耦合系數的推導
考慮兩個分別具有N1和N2匝長度為L1和L2的電感線圈。線圈1和2中的電流為I1和I2。假設由于電流I1在第二線圈中產生的磁通量為Φ21。則互感為M = N1 Φ21/ I1
Φ21可以描述為磁通Φ1與第二線圈相連的部分,即Φ21 = k1 Φ1
… M = N1 ( k1 Φ1) / i1 。. . . . . . . . . (1)
類似地,由于電流I2在第一線圈中產生的通量為Φ12,則互感為M = N2 Φ12/ I2
Φ21可以描述為磁通Φ1 與第二線圈相連的部分,即Φ12 = k2 Φ2
… M = N2 ( k2 Φ2) / i2 。. . . . . . . . . (2)
將等式 (1) 和 (2) 相乘,得到:
M = k1 k2 [N(1 Φ1 )/I_1 ].[N(2 Φ2 )/I2 ]
然后通過已知條件,可以推出耦合系數K= M/((√(L1 L2 )) )。
注意:
K值永遠不會是負數或永遠不會是小數值。
鐵芯或鐵氧體磁芯耦合電路的耦合系數為k=0.99
空芯耦合電路的耦合系數k=0.4~0.7
總結
電感器中的感應可以用楞次定律和法拉第定律來解釋。楞次定律指出,“在電流方向上產生的感應電動勢與產生該電動勢的磁通量相反”。線圈中的電感有兩種類型,它們是自感和互感。
線圈的自感是放置在電流變化電路中時在土壤中感應出的電動勢,這種自感現象稱為“自感”。用L表示,L = N Φ /I。
由于其耦合線圈的電流變化而在線圈中感應出電動勢的現象稱為“互感”,用M表示,M = √(L1 L2 )
兩個線圈之間的電感耦合量用“耦合系數”表示。耦合系數的值將小于1并始終大于0,用“k”表示,K = M/((√(L1 L2 )) )。
-
電容器
+關注
關注
64文章
6252瀏覽量
99999 -
電阻器
+關注
關注
21文章
3787瀏覽量
62228 -
電感器
+關注
關注
20文章
2335瀏覽量
70663
發布評論請先 登錄
相關推薦




 自感和互感的區別及其計算公式
自感和互感的區別及其計算公式
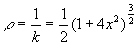












評論