隨著深度學(xué)習(xí)的發(fā)展，其應(yīng)用場景也越發(fā)的廣泛與多樣。這些多樣化的場景往往會對實際的部署提出更加“定制化”的限制。例如，自動駕駛汽車對人體識別的精度要求肯定比圖像識別動物分類的精度要求更加嚴(yán)苛，因為二者的應(yīng)用場景和錯誤預(yù)測帶來的后果截然不同。這些“定制化”帶來的差異，對于實際部署的模型在精度、速度、空間占用上有更具體的要求。在很多場景中由于部署的設(shè)備算力不強、內(nèi)存較小，導(dǎo)致對于模型的速度和空間占用具有嚴(yán)格要求，而經(jīng)過量化的模型具有速度快、空間占用小的特性，恰恰能滿足這種需求。

因此量化模型被廣泛使用在推理側(cè)，量化也成為了一個重要且非常活躍的研究領(lǐng)域。近期，MegEngine 開源了 4 bits 的量化的相關(guān)內(nèi)容，通過 MegEngine 4 bits 量化實現(xiàn)的 ResNet-50 模型在 ImageNet 數(shù)據(jù)集上的精度表現(xiàn)與 8 bits 量化模型相差無幾，并且速度是 TensorRT-v7 8 bits ResNet-50 模型的推理速度的 1.3 倍。這次實踐為 MegEngine 積累了 4 bits 量化的相關(guān)經(jīng)驗。同時，MegEngine 決定將 4 bits 量化的相關(guān)代碼開源，為大家提供可參考的完整方案，推動在更低比特推理領(lǐng)域的探索與發(fā)展。

背景

深度學(xué)習(xí)領(lǐng)域的模型量化是將輸入從連續(xù)或其他較大的值集約束到離散集的過程。量化具有以下兩點優(yōu)勢：

在存儲空間上，相較于 FLOAT 的 32 bits 的大小，量化值占用的空間更小。

在性能上，各類計算設(shè)備對量化值的計算能力要高于 FLOAT 的計算能力。

本文中提到的 n bits 量化，就是將 FP32 的數(shù)據(jù)約束到 n bits 表示的整型數(shù)據(jù)的過程。量化依據(jù)數(shù)據(jù)的映射特征可以分為線性量化和非線性量化，MegEngine 中采用的是線性量化，使用的量化公式和反量化公式如下：

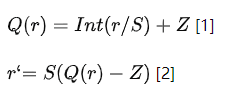
其中，Q 是量化方法，r 是真實獲取的輸入 FLOAT 值，S 是 FLOAT 類型的縮放因子，Z 是 INT 類型“零點”。

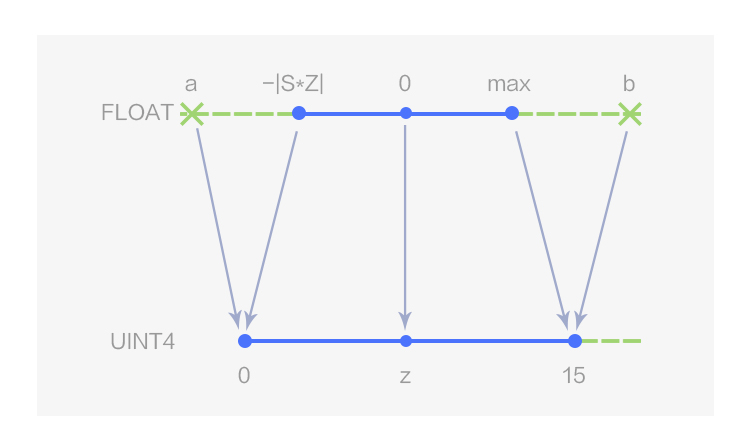
圖1 4 bits 非對稱線性量化

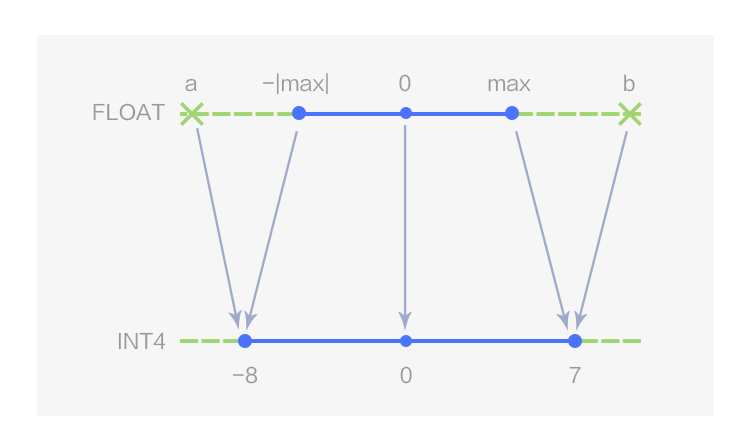
圖2 4 bits 對稱線性量化

如圖 1 所示，MegEngine 用數(shù)據(jù)類型 UINT4 表示 4 bits 的非對稱線性量化，量化值的取值范圍為[0,15]；當(dāng) Z 取 0 時即為對稱線性量化，此時 4bits 量化值的取值范圍為[-8, 7]，在 MegEngine 中用數(shù)據(jù)類型 INT4 表示，如圖 2 所示。

目前 8 bits 量化模型在一些場景下被業(yè)界廣泛運用，我們想去了解 4 bits 量化模型的落地的可能性。這要解決兩個問題：一方面，4 bits 量化模型的精度要如何保證；另一方面，4 bits 量化模型的速度能提升多少。要解答這兩個問題，需要算法研究員和工程開發(fā)人員的通力協(xié)作進行驗證。整件事情投入高，收益不明確。我們想找到開源代碼，快速從原理層面對這兩個問題有個判斷，但經(jīng)過調(diào)研發(fā)現(xiàn)目前并沒有 4 bits 量化相關(guān)開源內(nèi)容可供研究參考。所以，MegEngine 決定開發(fā) 4 bits 量化并解答這兩方面的問題。

緩解精度下降

保證 4 bits 量化模型的精度是重中之重，如果模型精度無法滿足需求，則 4 bits 量化的開發(fā)將毫無意義。為了避免精度的大幅下降，MegEngine 采取的舉措是輸入和輸出采用非對稱量化 UINT4，weights 采用對稱量化 INT4，bias 采用 FP32。接下來，從計算公式的推演上，來看這樣設(shè)計的合理性：

FP32 原始計算一次卷積輸出結(jié)果的公式：

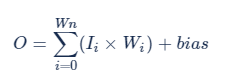
結(jié)合公式 [1]、[2] 推導(dǎo)的 4 bits 量化的公式：

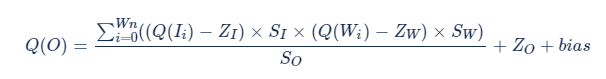
優(yōu)化之后的公式：

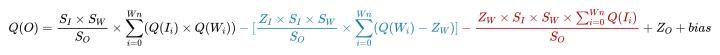
在上述公式中，ZI、ZW 是否等于 0，表明輸入/輸出和 weights 采用 INT4 還是 UINT4。并且在該公式中，除了Q(Ii)的值需要推理時確定，其余值均可在推理前獲得。所以，依據(jù)數(shù)據(jù)的計算特性，將這個公式分為了三個部分，分別用三種顏色表示：

黑色表示無論輸入/輸出以及 weights 數(shù)據(jù)類型如何選擇，一定有的計算量。因為無法避免，所以不用考慮這部分的數(shù)據(jù)特性。

藍(lán)色表示可以在推理前計算好的數(shù)據(jù)。

紅色表示必須在推理時才能計算的數(shù)據(jù)。

推理前可以計算好的這部分?jǐn)?shù)據(jù)可以提前計算并融合進 bias 中加入后續(xù)計算，所以 bias 必須用 FP32 數(shù)據(jù)類型表示，否則精度會大大降低。

至于輸入/輸出以及 weights 的數(shù)據(jù)類型選擇，結(jié)合上述公式可以推導(dǎo)得出：

全用 INT4 時，即ZI、ZW 均等于 0， 計算量最小，只有黑色部分公式。

輸入/輸出用 UINT4，weights 用 INT4，即ZI 不等于 0，ZW 等于 0 時，會增加藍(lán)色公式部分的計算量，但是這個部分是可以提前運算好的，對整體計算時間影響不大。

weights 用 UINT4，即ZW 不等于 0 時， 會增加紅色公式部分的計算量，會對整體的計算時間帶來較大影響。

由于 ResNet-50 模型 conv_relu 算子中的 relu 操作，輸入/輸出層的數(shù)據(jù)比較符合非對稱的特性，采用非對稱量化能更好地保留數(shù)據(jù)信息減少精度損失，所以輸入/輸出應(yīng)該選擇 UINT4，排除了上面三種方案中的第一種。第三種方案計算量會大很多，但是對精度的收益并不明顯。所以，最終選擇輸入和輸出采用非對稱量化 UINT4，weights 采用對稱量化INT4的方案。

緩解精度下降

提升模型性能并非一個簡單的“因為計算設(shè)備的 4 bits 算力大于 8 bits 算力，所以易知......”的推導(dǎo)，計算設(shè)備 4 bits 算力大于 8 bits 算力是已知的，但是需要一些方法將這部分的算力“兌現(xiàn)”，算力需要合適的算子釋放出來，其次，4 bits 量化所追求的也并非在某個算子的性能上超過 8 bits 量化，而是在模型層次超越 8 bits 量化。考慮到ResNet-50 模型以及卷積算子非常具有代表性，我們最終決定用 ResNet-50 模型作為基準(zhǔn)測試模型。經(jīng)過對模型的分析，發(fā)現(xiàn) ResNet-50 模型的性能瓶頸主要集中在兩個方面：

小算子比如 relu、add 較多，這些細(xì)瑣算子帶來的啟動以及帶寬上的開銷較大。

conv 計算非常多，占用了全圖 80% 以上的運算時間。

為解決這兩方面的瓶頸，MegEngine 做了以下兩個方面的優(yōu)化工作：圖層次的算子融合以及算子層次的優(yōu)化。

算子融合優(yōu)化

MegEngine 通過對計算圖進行掃描匹配，并將匹配到的圖結(jié)構(gòu)替換為優(yōu)化后的圖結(jié)構(gòu)。ResNet-50 模型所用的兩種 pass 轉(zhuǎn)換如下圖所示:

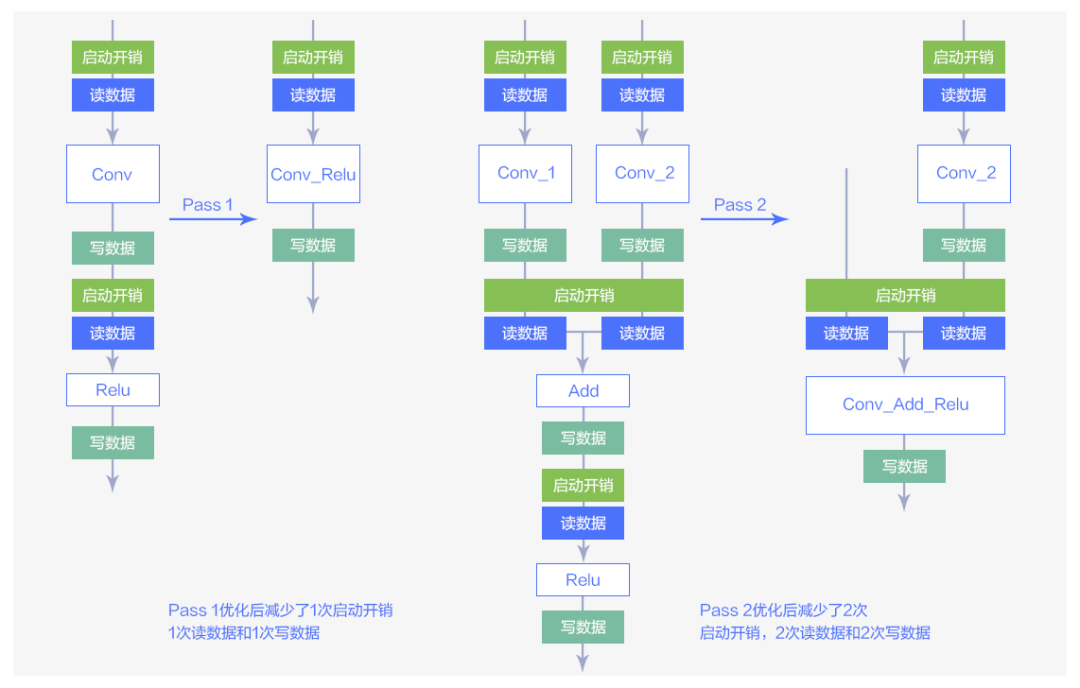
圖3 兩種Pass優(yōu)化方法

圖 3 中的大方塊表示圖中各種算子，小方塊表示這些算子的讀/寫數(shù)據(jù)操作以及啟動開銷。從圖中可以看到經(jīng)過算子融合的優(yōu)化可以有效減少算子的讀/寫數(shù)據(jù)的操作以及啟動開銷。

將這兩個 pass 應(yīng)用于原始的 ResNet-50 的結(jié)構(gòu)，就可以得到優(yōu)化后的圖。

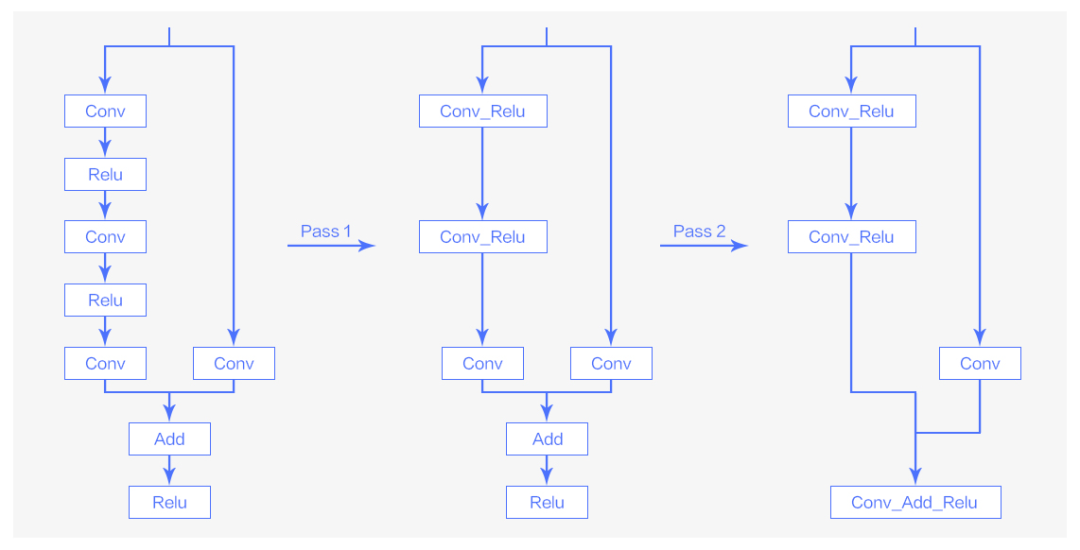
圖4 Pass優(yōu)化在ResNet-50模型中的應(yīng)用

從圖 4 可以看到，通過對 ResNet-50 模型的網(wǎng)絡(luò)結(jié)構(gòu)的優(yōu)化，add 和 relu 這些計算強度較小的算子已經(jīng)被 conv 這種計算強度大的算子所吸收，減少了小算子帶來的啟動以及讀寫上的開銷。

conv 算子優(yōu)化

經(jīng)過算子融合優(yōu)化后，可以看到 ResNet-50 模型調(diào)用的算子主要是各種 conv fuse 的算子，如 Conv_Relu、Conv_Add_Relu，這些算子的主體部分都是 conv，所以主要的優(yōu)化也都落實在了 conv 算子優(yōu)化上。

conv 采用 implicit gemm 算法并通過 mma 指令調(diào)度 tensor core 進行計算加速。顧名思義，implicit gemm就是將 conv 運算轉(zhuǎn)換為矩陣乘的一種算法，是對 img2col 的算法的改進，傳統(tǒng)的 img2col 算法如下：

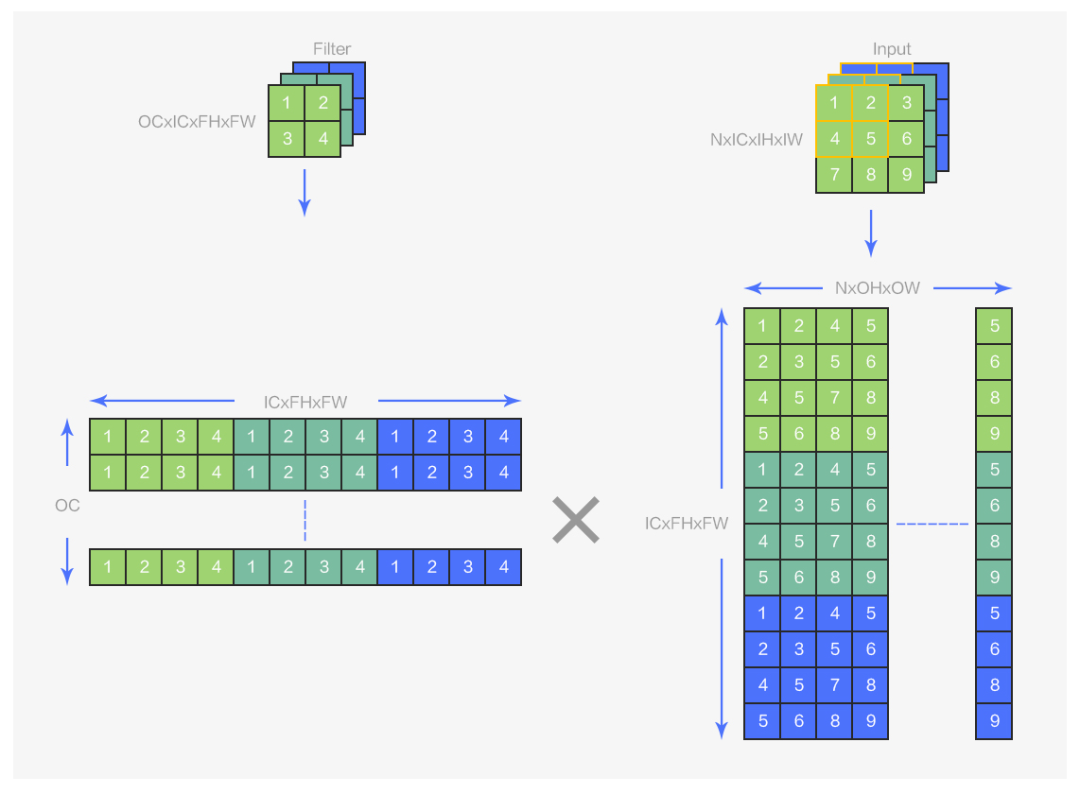
圖5 img2col示意圖

從圖 5 中可以看到，img2col 是將輸入 shape 為（N,IC,IH,IW），卷積核 shape 為（OC,IC,FH,FW）的卷積運算變?yōu)?shape 分別為（OC，ICFHFW）和（ICFHFW，NOHOW）的兩個矩陣的乘法運算。implict geem 的整體運算邏輯與 img2col 相同，其區(qū)別在于 img2col 會“顯式”地完成圖 6 中數(shù)據(jù)的卷積排布到矩陣排布的轉(zhuǎn)換，需要額外開辟一塊矩陣大小的空間用以存儲轉(zhuǎn)換后的矩陣，implict gemm 的轉(zhuǎn)換則是“隱式”的，沒有這部分空間開銷，在 implicit gemm 算法中并沒有開辟額外的空間存儲卷積核矩陣（OCxICFHFW）和輸入矩陣（ICFHFWxNOHOW），而是在分塊后，每個 block 會按照上圖中的對應(yīng)邏輯，在 global memory 到 shared memory 的加載過程中完成從數(shù)據(jù)的原始卷積排布到 block 所需的矩陣分塊排布的轉(zhuǎn)換。

針對 4 bits 的 implict gemm 的優(yōu)化主要參照 cutlass 的優(yōu)化方案，并在此基礎(chǔ)上加入了 output 重排的優(yōu)化。由于篇幅問題，本節(jié)僅講解 output 重排的優(yōu)化，想要了解更多技術(shù)細(xì)節(jié)，建議參考閱讀之前的文章以及開源代碼。

先分析 output 目前的排布情況，implict geem 的計算最終都落實在了 mma 指令上，而 mma 指令輸出的排布與 warp 中 32 個線程的關(guān)系如下：

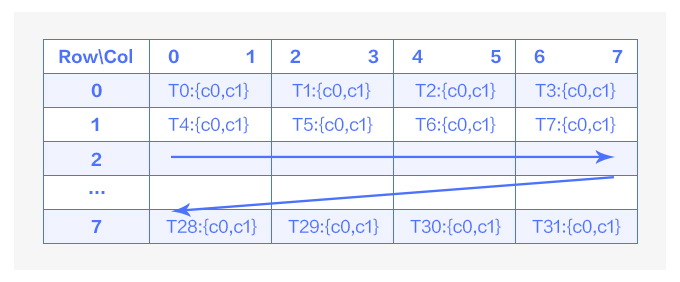
圖6 mma輸出排布示意圖

如圖 6 中所示，在一次 mma 指令運算中，一個 warp 的 32 個線程負(fù)責(zé) 64 個運算結(jié)果，且這些結(jié)果都存儲在寄存器上。每個線程負(fù)責(zé) 8x8 的結(jié)果矩陣同一行內(nèi)連續(xù)的兩個運算結(jié)果，每四個線程負(fù)責(zé)同一行的 8 個運算結(jié)果。

結(jié)合 implict geem 的結(jié)果矩陣 OCxNOHOW（由 OCxICFHFW 和 ICFHFWxNOHOW 乘積得到），在MegEngine 4 bits 量化的卷積算子設(shè)計中，一個 warp 的 32 個線程和輸出的排布關(guān)系如下：

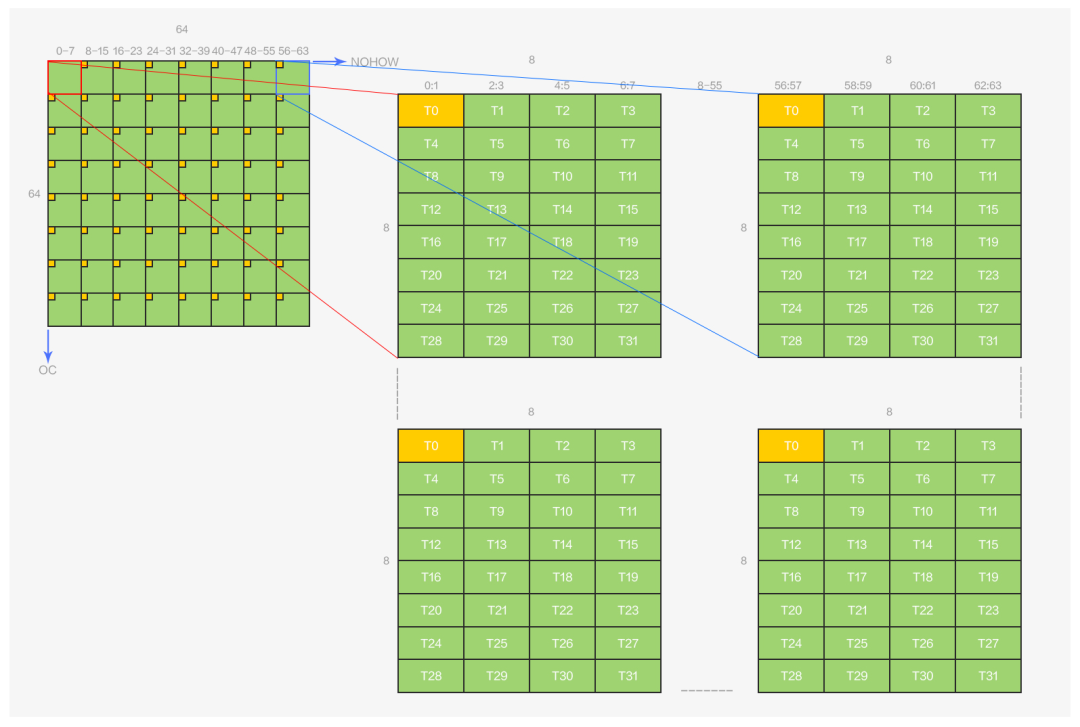
圖7 warp輸出排布示意圖

一個 warp 負(fù)責(zé) 64x64 大小的輸出矩陣，該矩陣由 8x8 個 mma 的 8x8 輸出矩陣組成，輸出和線程的排布關(guān)系如圖所示，黃色部分表示線程 0 所擁有的數(shù)據(jù)。圖 7 中的所有數(shù)據(jù)都在寄存器上，算子的最后一步操作，也就是將這些數(shù)據(jù)寫回到 global memory 上并按照 NCHW64 的方式進行排布。

一眼看上去，這些數(shù)據(jù)的排布都是間隔開的，雖然橫坐標(biāo)上的數(shù)據(jù)連續(xù)，但對于寫回到 global memory 并按照 NCHW64 排布而言，并沒有什么幫助。直接的寫回方式是將這些寄存器上的數(shù)據(jù)進行壓縮，先將 8 個32 bits的數(shù)據(jù)轉(zhuǎn)換為 8 個4 bits 的數(shù)據(jù)，再將這 8 個 4 bits 的數(shù)據(jù)放到一個 32 bits 大小的空間，然后寫回到 global memory，這種處理方式將面臨幾個問題：

每個線程中的數(shù)據(jù)都不連續(xù)，增大了數(shù)據(jù)處理難度，這些額外的處理計算可能會導(dǎo)致性能下降。

需要在縱向的 8 個線程間交換數(shù)據(jù)，會有同步的開銷。

這無疑是一個開銷比較大的處理方式，為了解決寫回數(shù)據(jù)帶來的性能問題，MegEngine 采用了以下處理方式：

注意到 NCHW64 的排布方式，每 64 個 OC 是連續(xù)的，嘗試將矩陣旋轉(zhuǎn)一下，想象這是一個 NOHOWxOC 的矩陣，那么 T0、T1、T2、T3 四個線程所負(fù)責(zé)的數(shù)據(jù)在 OC 維度上是連續(xù)的，它們對于的 OC 維度分別是

T0{0,1; 8,9;16,17;24,25;32,33;40,41;48,49;56,57}、

T1{2,3;10,11;18,19;26,27;34,35;42,43;50,51;58,59}......

可以看到，現(xiàn)在是四個線程負(fù)責(zé) 64 個連續(xù)的輸出，那么只要這四個線程交換數(shù)據(jù)再壓縮、寫回即可。相比于之前 8 個線程間數(shù)據(jù)交換和寫回，現(xiàn)在的處理方式更加簡單，內(nèi)部偏移計算與同步開銷會更少。所以實現(xiàn)output轉(zhuǎn)置是一種切實可行的優(yōu)化方法。這也體現(xiàn)了 NCHW64 的排布方式使得 4 bits 類型的數(shù)據(jù)在傳輸過程能被連續(xù)訪存，充分利用硬件資源的特點。

但是線程間交換數(shù)據(jù)的開銷在output轉(zhuǎn)置處理中依然沒有被徹底解決。如果可以得到

T0{0,1;2,3;4,5;6,7;8,9;10,11;12,13;14,15}、

T1{16,17;18,19;20,21;22,23;24,25;26,27;28,29;30,31}......

這樣的輸出OC 維度和線程對應(yīng)關(guān)系。那么就只需要在線程內(nèi)部進行數(shù)據(jù)打包和寫回，并且 16 個4 bits 的數(shù)據(jù)正好占用 2 個32 bits 大小的空間，非常規(guī)整。要實現(xiàn)這個效果也是非常簡單的：對于 AxB=C 的矩陣乘法，要實現(xiàn) C 矩陣的列順序變換，只需要對 B 矩陣進行對應(yīng)的列順序變換即可，如下圖所示：

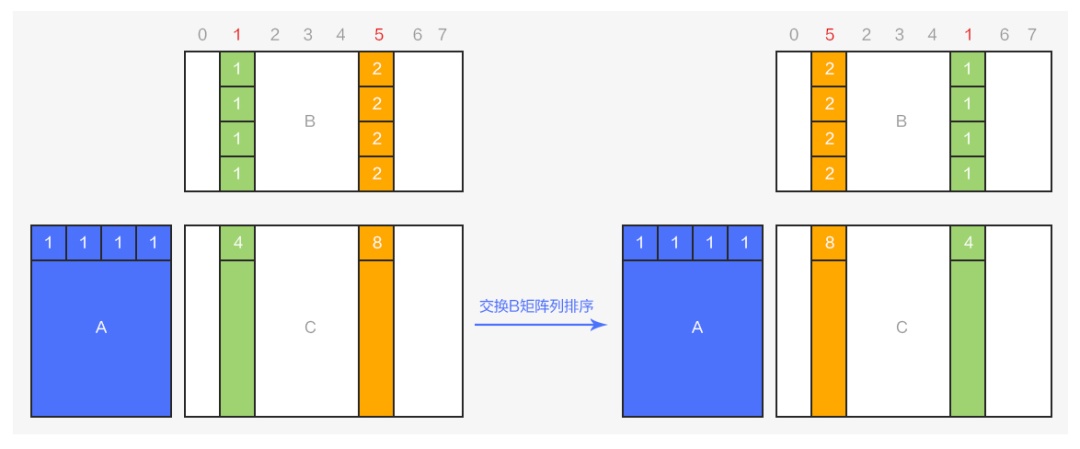
圖8 矩陣乘積的列變換

從圖 可以看出，將乘積矩陣 AxB=C 中的 B 矩陣的第1列和第5列進行對調(diào)，結(jié)果矩陣 C 對應(yīng)的列的運算結(jié)果也會發(fā)生同步的對調(diào)。利用這一特點，可以在 conv 算子運算前，將 weights 的列進行重排序，使得最終輸出OC 維度在對應(yīng)的相同線程中保持連續(xù)，T0{0,1;2,3;4,5;6,7;8,9;10,11;12,13;14,15}...

所以總結(jié)一下 output 重排的策略，其實就兩點：

將 OCxICFHFW 和 ICFHFWxNOHOW 的矩陣乘，變?yōu)?NOHOWxICFHFW 和 ICFHFWxOC 的矩陣乘，實現(xiàn)output 結(jié)果的轉(zhuǎn)置，確保在 OC 維度上的數(shù)據(jù)連續(xù)，配合 NCHW64 的排布方式，便于將數(shù)據(jù)從寄存器上寫回到 global memory 上。

通過對 ICFHFWxOC 矩陣的 OC 進行重新排序，實現(xiàn) output 矩陣 NOHOWxOC 的 OC 維度和線程的對應(yīng)關(guān)系更加合理，確保線程內(nèi)部的數(shù)據(jù)連續(xù)性，避免線程間數(shù)據(jù)交換的開銷。

總結(jié) & 展望

本次開源提供了和 TensorRT(TRT) ResNet-50 8 bits 量化模型在 ImageNet 數(shù)據(jù)集上速度以及精度對比結(jié)果：

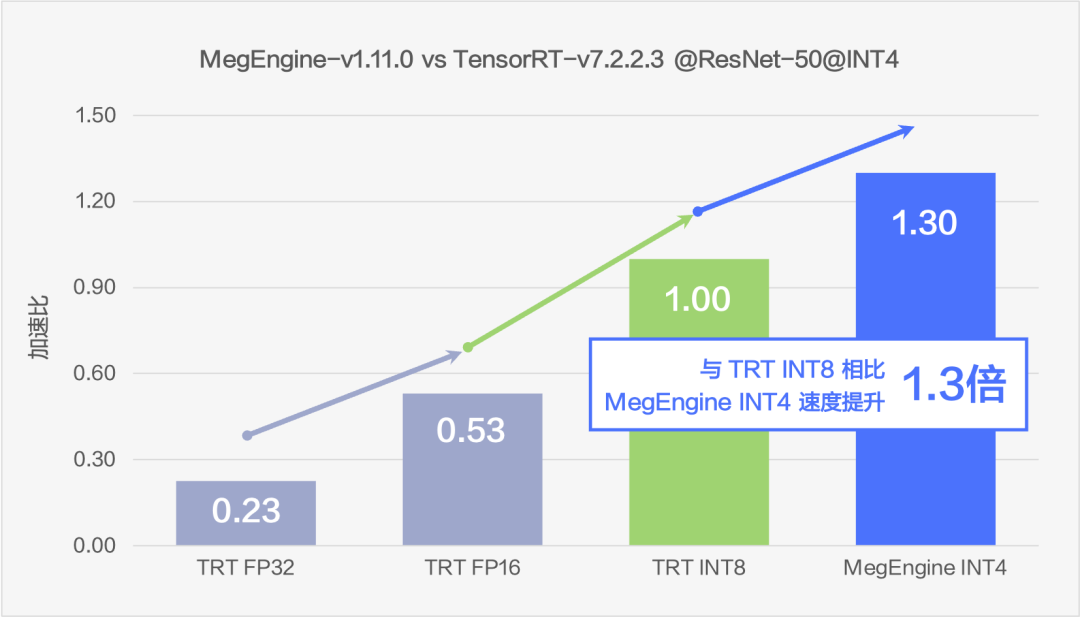
圖9 速度對比

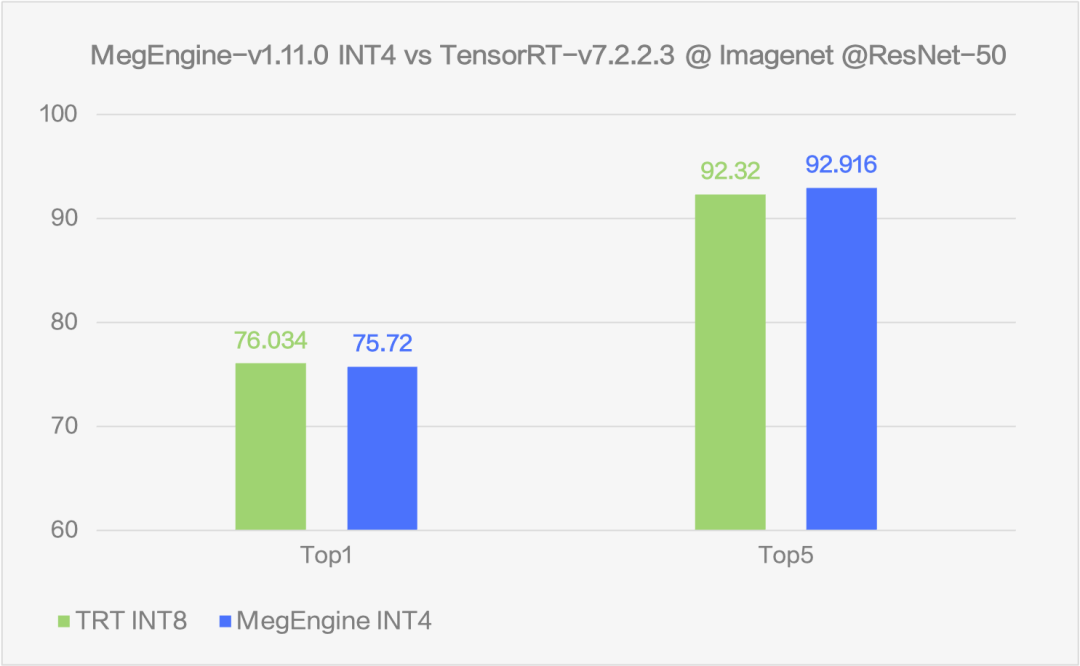
圖10 精度對比

通過在 ResNet50 上的測試可以看到，MegEngine 的 INT4 方案可以比 fp32 推理速度提升 5.65 倍至多，相比于現(xiàn)在業(yè)內(nèi)較為常用的 INT8 方案也仍然可以提升 1.3 倍的速度。在速度大幅提升的同時，uint4*int4 的方案盡可能的保證了精度，精度下降能夠控制在 top1 -0.3% 左右。

在速度和精度兩方面的努力，讓 INT4 的方案能夠在實際的業(yè)務(wù)場景中帶來顯著的優(yōu)勢，而不只是停留在論文上。

審核編輯 ：李倩