在這篇文章中,我們討論另外一個困擾神經網絡訓練的問題,病態曲率。
雖然局部極小值和鞍點會阻礙我們的訓練,但病態曲率會減慢訓練的速度,以至于從事機器學習的人可能會認為搜索已經收斂到一個次優的極小值。讓我們深入了解什么是病態曲率。
病態曲率
考慮以下損失曲線圖。
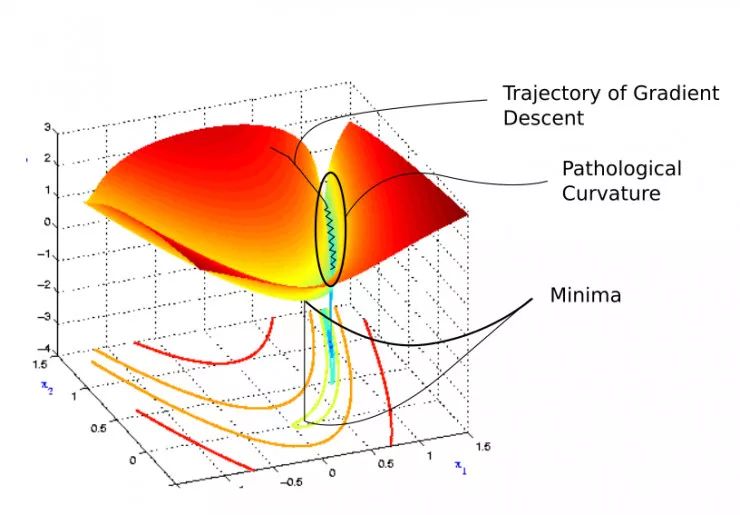
**病態曲率**
如你所知,我們在進入一個以藍色為標志的像溝一樣的區域之前是隨機的。這些顏色實際上代表了在特定點上的損失函數的值,紅色代表最高的值,藍色代表最低的值。
我們想要下降到最低點,因此,需要穿過峽谷。這個區域就是所謂的病態曲率。為了了解為何將其稱為病態曲率,讓我們再深入研究。放大了看,病態曲率就像這樣...
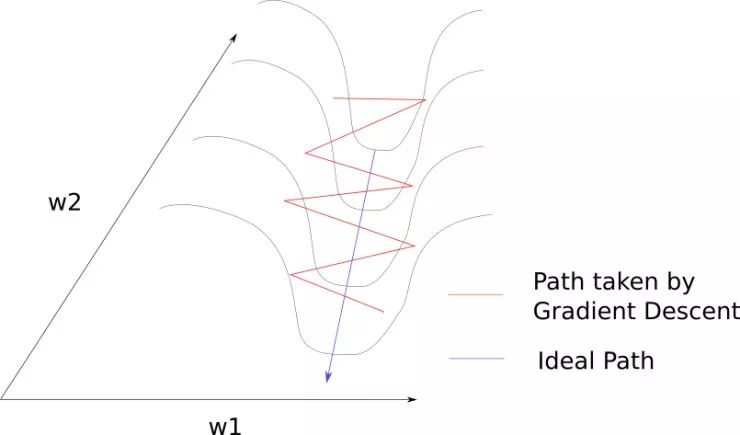
**病態曲率**
要知道這里發生的事情并不難。梯度下降沿著峽谷的山脊反彈,向最小的方向移動的速度非常慢。這是因為山脊的曲線在 W1 方向上彎曲的更陡。
考慮山脊表面的 A 點。我們看到,梯度在這點可以分解為兩個分量,一個沿著 W1 方向,另外一個沿著 W2 方向。如果 f 顯著下降的唯一方向是低曲率的,那么優化可能會變得太慢而不切實際,甚至看起來完全停止,造成局部最小值的假象。
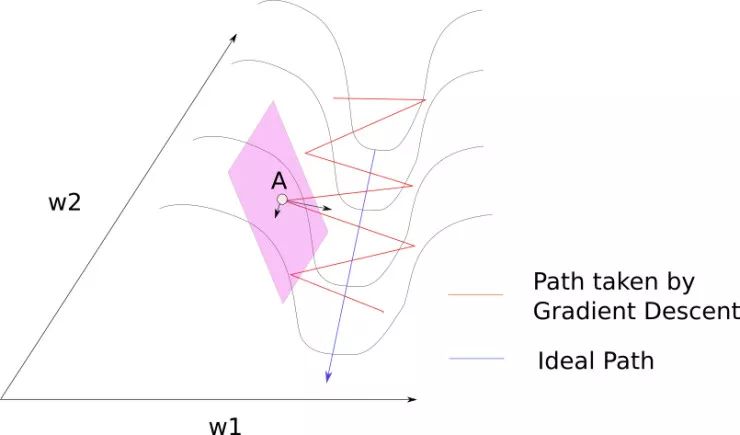
正常情況下,我們使用一個較慢的學習率來解決這種山脊間反彈的問題,正如上一篇關于梯度下降的文章所述。然而,這卻產生了麻煩。
當我們接近最小值時,慢下來是有意義的,我們想要收斂于它。但是考慮一下梯度下降進入病態曲率的區域,以及到最小值的絕對距離。如果我們使用較慢的學習率,可能需要花費更多的時間才能到達極小值點。事實上,有研究論文報道過使用足夠小的學習率來阻值山脊間的反彈可能導致參與者以為損失根本沒有改善,從而放棄訓練。
如果 f 顯著下降的唯一方向是低曲率的,那么優化可能會變得太慢而不切實際,甚至看起來完全停止,造成局部最小值的假象。
也許我們想要的是能讓我們慢慢進入病態曲率底部的平坦區域,然后在最小值的方向上加速。二階導數可以幫助我們做到這一點。
牛頓法
梯度下降是一階優化方法。它只考慮損失函數的一階導數,而不考慮更高階的導數。這基本上意味著它不知道損失函數的曲率。它只能說明損失是否下降以及下降的速度,而不能區分曲線是平坦的,向上的,還是向下的。

之所以會發生這種現象,是因為梯度下降只關心梯度,就好像上圖中紅色的點,三個曲線在這一點上的梯度是相同的。如何解決?使用二階導數,或者考慮梯度變化的速率。
一個非常流行的可以使用二階導數的技術,可以解決我們的問題,這個方法稱為牛頓法。如果表面變得不那么陡峭,那么學習步驟就會減少。
牛頓法可以提供一個理想的步長,在梯度方向上移動。由于我們現在有了關于損失表面曲率的信息,所以可以選擇步長,而不是用病態曲率來超過該區域的極限。
牛頓法通過計算 Hessian 矩陣來實現,Hessian 矩陣是損失函數的二階導數組成的權值組合。我所說的權值組合,如下所示。
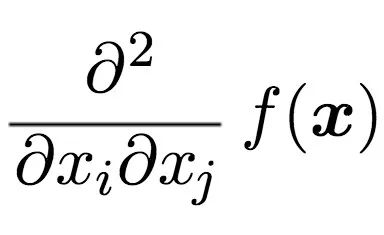
Hessian 矩陣在一個大矩陣中計算所有這些梯度。
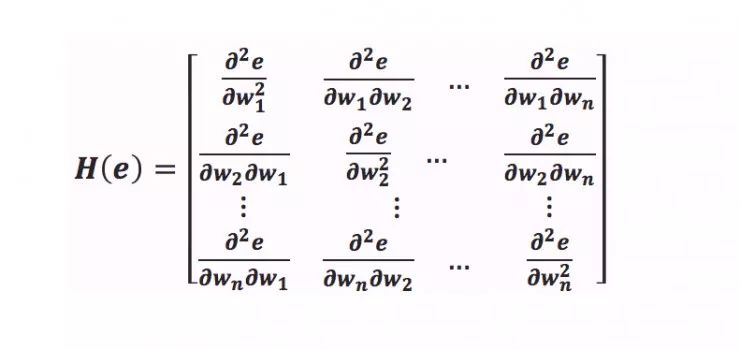
Hessian 矩陣給出了一個點的損失曲面曲率的估計。一個損失的表面可以有一個正曲率,這意味著當我們移動時,表面會迅速變得不那么陡峭。如果我們有一個負曲率,這意味著當我們移動時,曲面變得越來越陡。
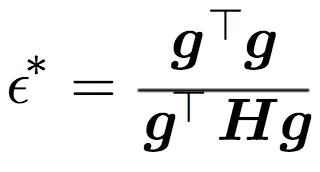
注意,如果這一步是負的,那就意味著我們可以使用任意的步驟。換句話說,我們可以切換回原來的算法。這對應于下面的情況,梯度變得越來越陡。

然而,如果梯度變得不那么陡峭,我們可能會走向一個處于病態曲率底部的區域。在這里,牛頓法給了我們一個修正的學習步驟,正如你所看到的,它與曲率成反比,或者曲面變得越來越小。
如果表面變得不那么陡峭,那么學習步驟就會減少。
為什么我們很少使用牛頓法? 看到公式中的 Hessian 矩陣了嗎?Hessian 矩陣需要計算損失函數對所有權值組合的梯度。在組合已知的情況下,要求的值的數量約是神經網絡中權值數量的平方。
對于現代的網絡來說,通常都含有數十億個參數,使用高階的優化方法很難計算 10 億的平方數量級的梯度。
二階優化是關于梯度本身如何變化的信息。雖然我們不能精確的計算它,但是我們可以遵循啟發式方式,以指導我們根據之前的梯度進行優化。
Momentum
與 SDG 結合使用的一種常用方法叫做Momentum。Momentum 不僅會使用當前梯度,還會積累之前的梯度以確定走向。梯度下降方程修改如下。
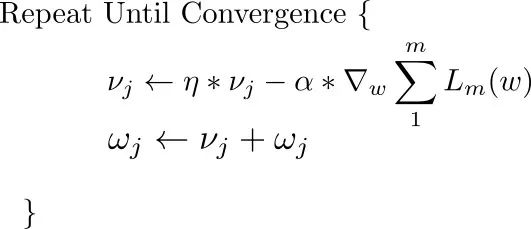
第一個式子有兩項。第一項是上一次迭代的梯度,乘上一個被稱為「Momentum 系數」的值,可以理解為取上次梯度的比例。

我們設 v 的初始為 0,動量系數為 0.9,那么迭代過程如下:
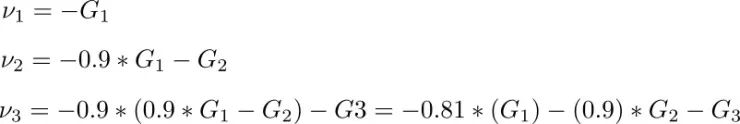
我們可以看到之前的梯度會一直存在后面的迭代過程中,只是越靠前的梯度其權重越小。(說的數學一點,我們取的是這些梯度步長的指數平均)。
這對我們的例子有什么幫助呢?觀察下圖,注意到大部分的梯度更新呈鋸齒狀。我們也注意到,每一步的梯度更新方向可以被進一步分解為 w1 和 w2 分量。如果我們單獨的將這些向量求和,沿 w1 方向的的分量將抵消,沿 w2 方向的分量將得到加強。
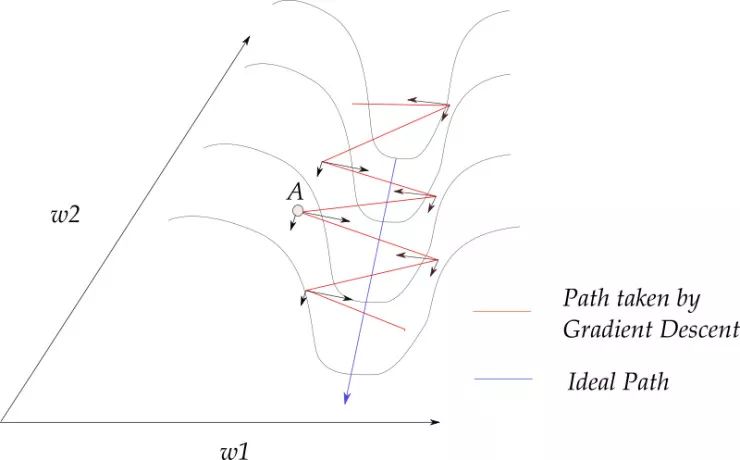
對于權值更新來說,將沿著 w2 方向進行,因為 w1 方向已抵消。這就可以幫助我們快速朝著極小值方向更新。所以,動量也被認為是一種抑制迭代過程中鋸齒下降問題的技術。
這種方法還可以提高收斂速度,但如果超過極小值,可能需要使用模擬退化算法
我們通常初始化動量為 0.5,并且在一定循環次數后逐漸退火到 0.9。
RMSProp
RMSProp 或均方根反向傳播算法有著有趣的歷史。它是由傳奇人物Geoffrey Hinton提出的,當時只是在課堂上是隨意提出的一個想法。
RMSProp 算法也旨在抑制梯度的鋸齒下降,但與動量相比, RMSProp 不需要手動配置學習率超參數,由算法自動完成。更重要的是,RMSProp 可以為每個參數選擇不同的學習率。
在 RMSprop 算法中,每次迭代都根據下面的公式完成。它是對每個參數單獨迭代。

讓我們來看看上面的方程都在做什么。
在第一個方程中,我們計算一個梯度平方的指數平均值。由于我們需要針對每個梯度分量分別執行平方,所以此處的梯度向量 Gt 對應的是正在更新的參數方向的梯度各個方向的投影分量。
為此,我們將上一次更新的超參數乘希臘字母 nu。然后將當前的梯度平方乘(1-nu)。最后我們將他們加到一起得到這一時刻的指數平均。
我們之所以使用指數平均是因為在 momentum 例子中看到的那樣,它可以使得間隔和權重成正比例變化。實際上使用「指數」一詞是因為前面項的權重呈指數級下降(最近的項權重是 ρ,次近的 ρ 方,然后是 ρ 立方,以此類推)。
注意我們表示病態曲率的圖,梯度沿 w1 方向的分量比沿 w2 方向的分量大的多。我們以平方的方式將 w1 和 w2 疊加,w1 不會發生抵消,w2 在指數平均后會更小。
第二個方程定義了步長,我們沿負梯度方向移動,但是步長受到指數平均值的影響。我們設置了一個初始學習率 eta,用它除指數平均值。在我們的例子中,因為 w1 平均后比 w2 大很多,所以 w1 的迭代步長就比 w2 要小很多。因此這將避免我們在山脊之間跳躍而朝著正確的方向移動。
第三個方程是更新操作,超參數 p 通常選為 0.9,但是你可能需要調整它。方程 2 中的 epsilon 是為了防止被 0 除,通常取 1e-10。
還要注意的是,RMSProp 隱含的執行模擬退火,假設我們正朝著極小值前進并且我們想要放慢速度避免越過極小值。當步長很大時 RMSProp 將自動減小梯度更新的步長(大步長容易越過極小值點)。
Adam
到目前為止,我們已經對比了 RMSProp 和 Momentum 兩種方法。盡管 Momentum 加速了我們對極小值方向的搜索,但 RMSProp 阻礙了我們在振蕩方向上的搜索。
Adam 或 Adaptive Moment Optimization 算法將 Momentum 和 RMSProp 兩種算法結合了起來。這里是迭代方程。

我們計算了每個梯度分量的指數平均和梯度平方指數平均(方程 1、方程 2)。為了確定迭代步長我們在方程 3 中用梯度的指數平均乘學習率(如 Momentum 的情況)并除以根號下的平方指數平均(如 Momentum 的情況),然后方程 4 執行更新步驟。
超參數 beta1 一般取 0.9 左右,beta_2 取 0.99。Epsilon 一般取1e-10。
結論
在這篇文章中,我們介紹了 3 種基于梯度下降法來解決病態曲率同時加快搜索速度的方法。這些方法通常稱為「自適應方法」,因為學習步驟會根據等高線拓撲進行調整。
在上面的三種方法中,盡管 Adam 算法在論文中被認為是最有前景的算法,但是 Momentum 方法貌似更主流一些。實踐結果表明,在給定損失函數的情況下,三種算法都能收斂到不同的局部最優極小值。但是用帶 Momentum 的 SGD 算法比 Adam 算法找到的極小值更加平坦,而自適應方法往往會收斂到更加尖銳的極小值點。平坦的極小值通常好于尖銳的極小值。
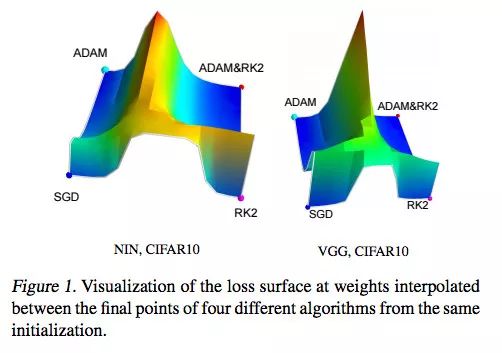
盡管自適應算法有助于我們在復雜的損失函數上找到極小值點,但這還不夠,特別是在當前網絡越來越來越深的背景下。除了研究更好的優化方法之外,還有一些研究致力于構建產生更平滑損失函數的網絡架構。Batch-Normalization 和殘差連接是其中的解決方法,我們也會盡快在博客上發布有關的詳細介紹。
-
神經網絡
+關注
關注
42文章
4771瀏覽量
100720 -
函數
+關注
關注
3文章
4329瀏覽量
62576
原文標題:深度學習優化入門:Momentum、RMSProp 和 Adam
文章出處:【微信號:vision263com,微信公眾號:新機器視覺】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
深入淺出地介紹了牛頓法、動量法、RMSProp、Adam優化算法
飛思卡爾曲率計算教程
曲率估計及在曲面檢測中的應用




 什么是病態曲率
什么是病態曲率
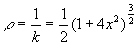










評論