一般來說，當(dāng)我們說到磁性時(shí)，我們認(rèn)為它是由移動(dòng)電荷產(chǎn)生的磁力線。假設(shè)有一根導(dǎo)線，并且有電流通過，就會(huì)產(chǎn)生一條圍繞電線的磁場線。如果我們在此區(qū)域引入一個(gè)移動(dòng)的帶電粒子，那么該粒子將由于磁場的存在而受到洛倫茲力。現(xiàn)在，我們把洛倫茲力的概念放在一邊，因?yàn)榻酉聛砦覀儗⒂昧硪环N方式來解釋這個(gè)力：狹義相對論下的靜電力。

想象一下，我們有一根導(dǎo)線和一個(gè)帶電粒子，粒子的速度為u。

情景一：導(dǎo)線中的正電荷和負(fù)電荷靜止不動(dòng)，它們的電荷線密度都是λ?，因此互相抵消不會(huì)對外界的帶電粒子產(chǎn)生靜電力。

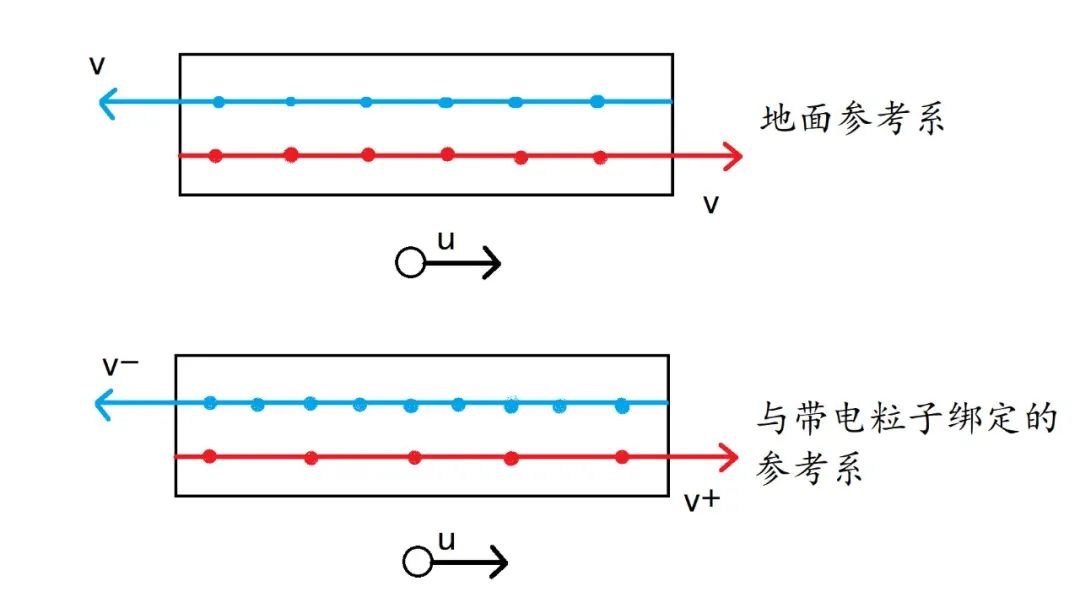
情景二，我們讓導(dǎo)線產(chǎn)生電流：正電荷以速度v向右移動(dòng)，負(fù)電荷以速度v向左移動(dòng)。雖然這個(gè)模型有點(diǎn)不實(shí)際，但計(jì)算很好用。從地面觀察者來看，由于狹義相對論的尺縮效應(yīng)，電荷之間的距離會(huì)縮小，因此線密度會(huì)變大。由于正電荷和負(fù)電荷速度大小一樣，因此它們的線密度都為λ，凈電荷密度為零，不會(huì)對外界帶電粒子產(chǎn)生靜電力。

現(xiàn)在，我們把參考系和導(dǎo)線外的帶電粒子綁定在一起。在這個(gè)參考系下的觀察者會(huì)看到，正電荷的移動(dòng)速度大小v+與負(fù)電荷的移動(dòng)速度大小v-不同，因此兩個(gè)正電荷之間的距離與兩個(gè)負(fù)電荷之間的距離不同，導(dǎo)致正電荷的線密度λ+就與負(fù)電荷的線密度λ-不同。所以，導(dǎo)線的橫截面就會(huì)有凈電荷產(chǎn)生，會(huì)對導(dǎo)線外的帶電粒子產(chǎn)生靜電力。

把以上的等式結(jié)合起來，我們能得到凈電荷密度λ_t的公式：

由上式我們可以看出，確實(shí)電荷密度不為零，所以會(huì)產(chǎn)生電場，帶電粒子就會(huì)受到靜電力。閉合曲面內(nèi)的電荷分布與產(chǎn)生的電場之間的關(guān)系可以由高斯定理算得。因此，我們沿著導(dǎo)線做一個(gè)半徑為r的圓柱面，根據(jù)高斯定理，可以得到帶電粒子處的場強(qiáng)，然后就可以得到粒子所受的靜電力：

接下來，我們要用到麥克斯韋方程組推導(dǎo)出來的光速公式c2=1/ε?μ?和上述提到的電流公式I=2λv，對受力公式進(jìn)行替換，可以得到：

請注意，這里的F'是在和帶電粒子綁定的坐標(biāo)系下，我們需要把它轉(zhuǎn)換到地面觀察者的坐標(biāo)系。

這就是與洛倫茲力相同的靜電力，只不過在地面觀察者看來，這像是導(dǎo)線電流產(chǎn)生的磁場而導(dǎo)致的力。我們還可以讓它和洛倫茲力的公式相等，就能得到導(dǎo)線產(chǎn)生的磁場強(qiáng)度：

這看起來是不是很熟悉，就是我們高中學(xué)過的畢奧—薩伐爾定律。

審核編輯：湯梓紅