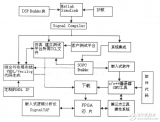
給出差分方程畫個圖吧。比如差分方程為y(n)=x(n)+5x(n-1)-4x(n-2)，畫出該系統的橫截型結構圖。什么是橫截型結構啊？這個時候還不知道，那就麻煩了，趕快到書中找這個知識點。這是最基礎的。再想想如何表達延時？有了這些概念，結構圖就能畫出來了。畫出結構圖，那么系統的功能就浮出了水面。

很多人到了大學就丟失了高中時期學習的習慣。在課上，你會發現沒有帶書帶本子的學生，就在那干坐著。我看了都覺得是在浪費時間。他是被逼著來的。但他的班主任能一直逼他學習嗎？那么多學生呢？不說了，該講什么知識就說什么知識吧。課后復習的情況幾乎沒有。這是我接觸到的現象，頭大啊！

接著上堂課回顧一下FFT的知識。比如能夠畫出長度N=4，采用基-2時間抽選法的FFT流圖嗎？回想一下上一堂課講的那張圖，請對照著畫一遍。

卷積！！！

在泛函分析中，卷積、旋積或摺積(英語：Convolution)是通過兩個函數f 和g 生成第三個函數的一種數學算子，表征函數f 與g經過翻轉和平移的重疊部分的面積。如果將參加卷積的一個函數看作區間的指示函數，卷積還可以被看作是“滑動平均”的推廣。那么在數字信號處理里面怎么用的呢？考試必考！！！估計同學們早已經忘了。

卷積的概念？

這個過程一定要牢記！！！給出知識總結的內容，希望同學們認真學習，從而真正的掌握！大學學習不僅要學理論，還要鍛煉思維！

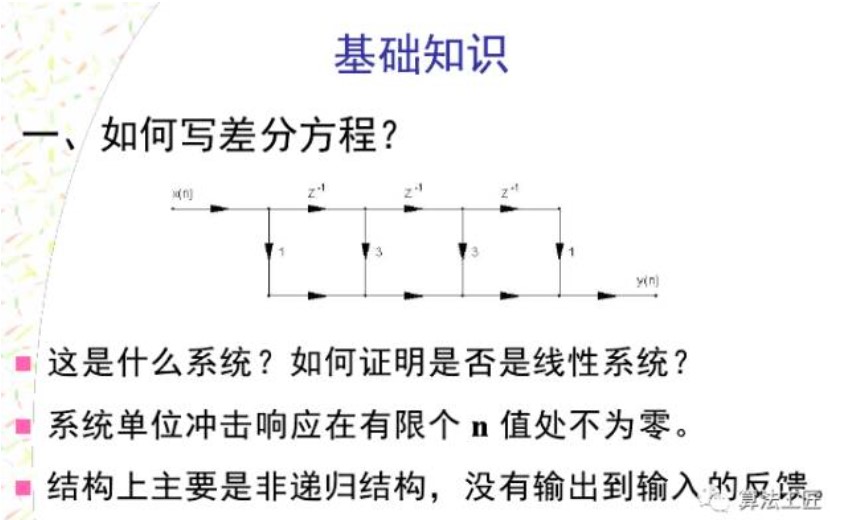
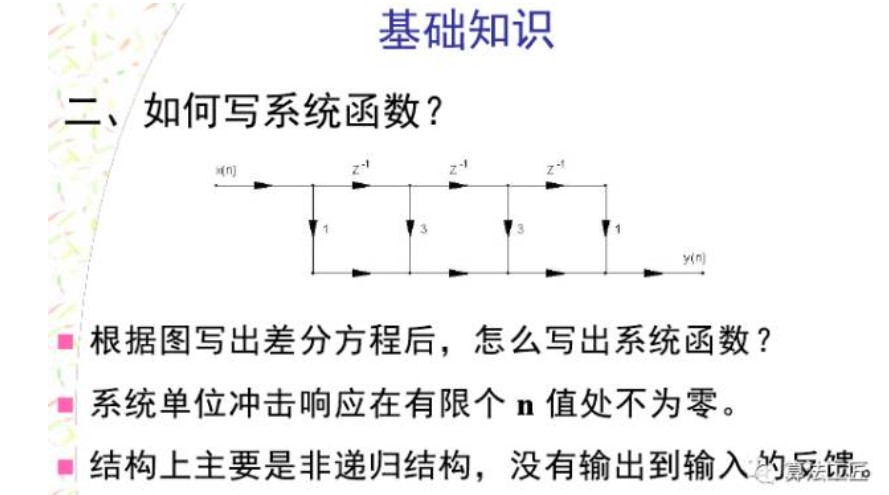
用單位脈沖響應h(n)可以表示線性時不變離散系統，這時 y（n）=x（n）*h（n）兩邊取z變換：Y(z)=X(z)H(z)則定義為系統函數。

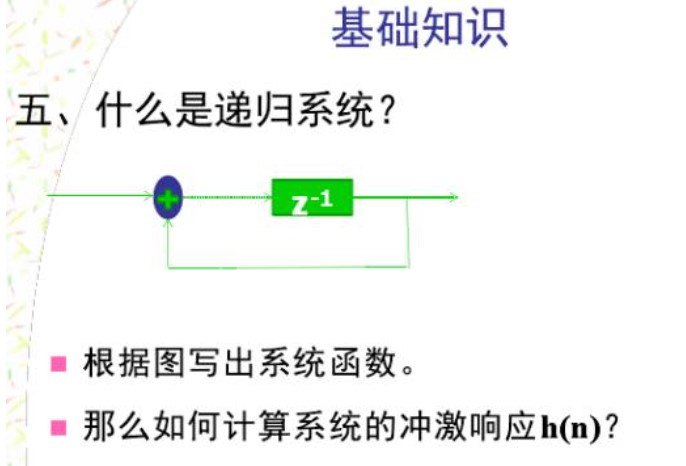
再次強調：用單位脈沖響應h(n)可以表示線性時不變離散系統，這時 y（n）=x（n）*h（n）兩邊取z變換：Y(z)=X(z)H(z)則定義為系統函數。它是單位脈沖響應的z變換。單位圓上的系統函數z=e就是系統的頻率響應。所以可以用單位脈沖響應的z變換來描述線性時不變離散系統。百度百科寫的很棒！

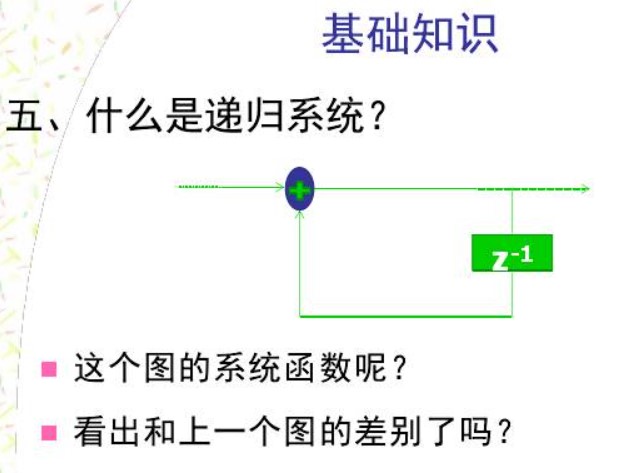
只有扎扎實實的做完這些題目，才能掌握數字信號處理的核心內容。未完，待續！

審核編輯：劉清