方差也稱為“平方差”，用來描述集合中變量的離散程度，即變量與平均值的偏離程度。方差越大，表示變量與平均值的偏離程度越大，即越不穩定。標準差是方差的算術平方根。今天這篇文章，我們就用SCL語言編寫函數來計算方差和標準差。

統計學上方差分為兩種：總體方差和樣本方差。

①總體方差：是指總體中每一個變量與總體平均值的差值的平方和，除以總體數量。總體方差的計算公式如下：

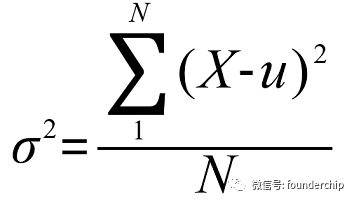
其中：σ2是總體方差，X是隨機變量，μ是總體均值，N是總體樣本量。

實際情況中，我們可能得不到總體的所有變量，只能抽取有限數量的樣本來代替整體，這種方差稱為樣本方差。

②樣本方差：樣本中所有變量與樣本平均值的差值的平方和，除以樣本數量（n-1）。樣本方差的計算公式如下：

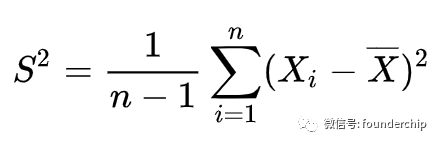
注意：樣本方差中為了實現對總體的無偏估計，除數采用樣本量減1。

③總體標準差：總體方差的算術平方根；

④樣本標準差：樣本方差的算術方法根；

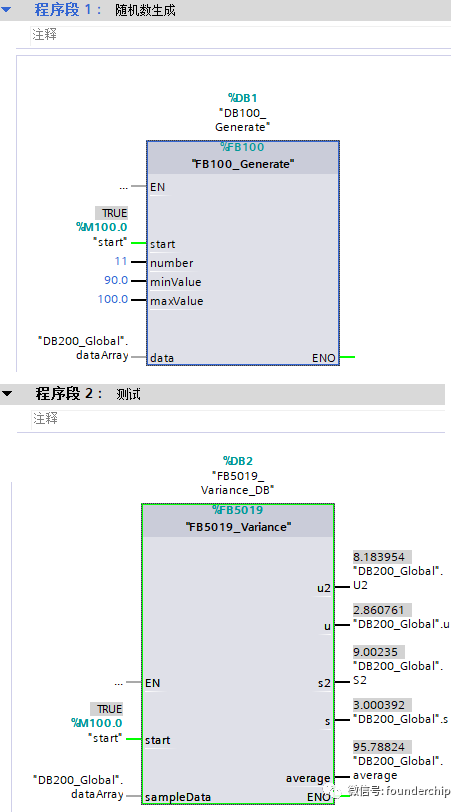
接下來編程實現總體方差/標準差及樣本方差/標準差的計算。

在博途環境下新建函數塊FB5019_Variance，聲明變量如下圖所示：

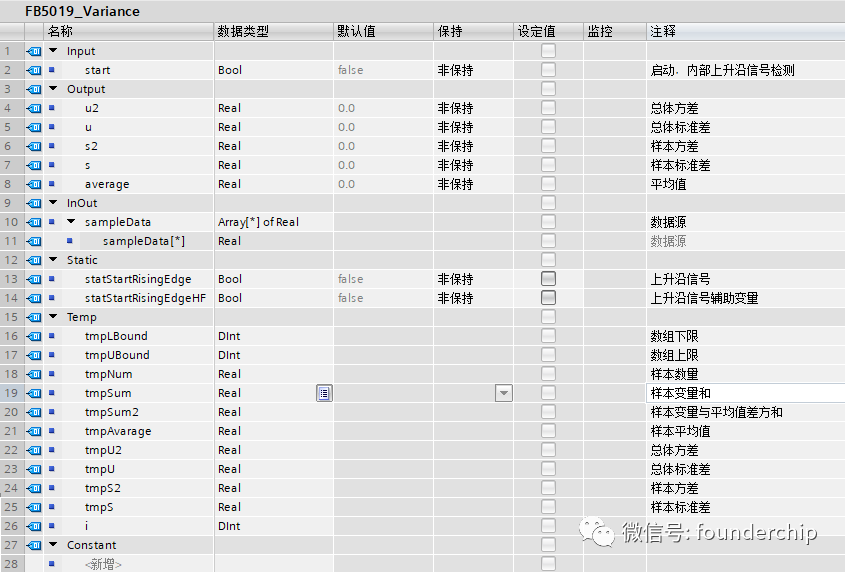
其中：

u2：總體方差；

u：總體標準差；

s2：樣本方差；

s：樣本標準差；

average：平均值；

編寫代碼如下：

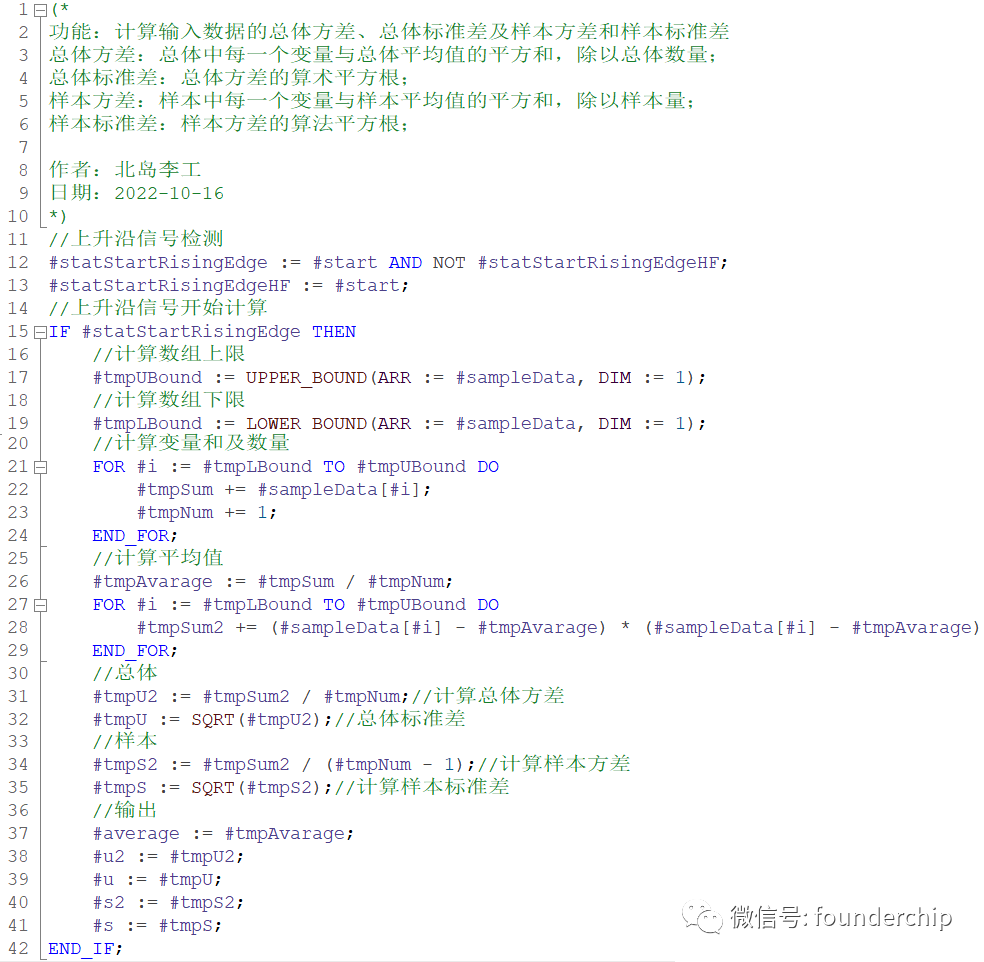
我使用隨機數產生函數測試過了這段代碼，如果你有任何問題歡迎留言討論。