Q值又叫品質因數,是衡量一個諧振回路或線圈的品質的重要參數。因為是個比值,所以是個不名數,只有數值,沒有單位。
如何計算?對諧振回路而言,Q值等于這個諧振回路線圈的電感量(亨利,H),除以:電容器電容量(法拉,F)乘以回路電阻(歐姆,Ω)的乘積。也就是說,諧振回路的線圈電感量越大、電阻和電容越小,諧振回路的Q值越高。
對線圈而言,Q值等于這個線圈的電感量,除以這個線圈的電阻值。也就是說,線圈要想提高Q值,可以換粗線繞(低頻)、或使用多股線繞(中頻中波段)、或蜂房繞法(減小分布電容)、或用鍍銀線間繞(高頻短波段)、或加磁芯(用長磁棒),都可以提高Q值。
提高Q值有何好處呢?因為線圈是諧振回路的一個組成部分,所以我們不用談線圈,只談諧振回路就可以了。Q值高了,諧振回路的選頻能力就強,收信機的靈敏度就高(可收到原來聽不到的遠地電臺),選擇性就好(不串音),性能就提高了。
可諧振回路的Q值也不是越高越好,因為Q值高,選頻的峰雖然高了,但通帶卻變窄了,同時穩定性變差,調好的電臺一松手就跑了。通帶變窄對中波短波以聽新聞語言為主的電臺當然無所謂了,這些電臺的頻寬只有9千赫(原來是10千赫,1978年改為中波段國際標準9千赫,短波段仍然保持10千赫);但對聽音樂為主的調頻電臺和電視臺就不行了,調頻電臺的帶寬250千赫,電視臺信號帶寬8000千赫,再使用原來的電路就不行了,增加帶寬的辦法有兩個:較好的方法是,使用多個不同頻率的調諧回路共同組成一個寬頻帶,這個方法在保證靈敏度和選擇性不變的前提下可以增加帶寬,缺點是線路復雜,要使用多級放大,簡單的方法是,向諧振回路上并聯一個電阻,并聯的這個電阻阻值越小,帶寬增加的越多,這個方法的優點是:簡單。缺點是:放大量顯著變小,靈敏度和選擇性明顯變劣。
關于諧振回路Q值的討論:線圈的Q值較好理解,同樣的電感量,電阻越小,震蕩起來損耗就越小,Q值肯定要高啦。但是對于諧振回路,為什么又把電容量弄到分母上,電容量越大反而Q值越低呀?電容也儲存電能呀,真是令人費解。
真實的情況是這樣的:諧振回路對某一頻率的交流電諧振是有條件的,就是線圈的電感量與電容器的電容量的乘積必須為一個固定值,當線圈對這個交流電的感抗與電容器對這個交流電的容抗一樣大時,因為二者方向相反,可以互抵,這個諧振回路就對這個頻率的交流電諧振了。有兩種方案可做比較:大電感配小電容,或小電感配大電容(因為要乘積為固定值)。第一種方案電路中電壓高,電流小,因為電感量大,所以同樣的電流能感應出高電壓,但電容量小存電量小形不成大電流,屬于高壓小電流方案;第二種方案電路中電壓低,電流大,因為電感量小所以同樣的電流只能感應出不高的電壓,但電容量大存電量多可以形成大電流,屬于低壓大電流方案。這樣就很清楚了,震蕩是電流在線圈與電容器之間來回跑,與高壓輸電原理相同,高壓小電流方案損耗必然小,Q值肯定高啦。
從理論上分析,Q值等于諧振回路的電抗的絕對值與電阻的比值。電抗越大、電阻越小諧振回路的Q值越高。線圈的感抗是和電感量成正比的,而電容器的容抗卻是和電容量成反比的,使用大電感量與小電容量組合成的諧振回路,可形成較大的電抗,是大感抗對大容抗互抵,從而形成高Q值。而使用小電感量與大電容量組合成的諧振回路,卻無法形成較大的電抗,是小感抗對小容抗互抵,從而Q值很低。





引言
寄生電感這個字眼就經常出現,特別是引線電感。我們解釋一些問題的時候都是直接套用的,默認它的存在。可實際上是,我在很長一段時間內并不理解它到底是怎么來的,因為我印象中電感都是線圈,而直導線并不是。直到之前不久我才思索了一番,算是有一些了解,也寫了下面一篇文章。
寄生電感怎么來的
最近一直在看電感和磁珠的內容,也有看LC濾波器,自然會有LC諧振的問題。LC串聯諧振,單獨拿出來說的話,可能會覺得太簡單了,這有啥好說的。自然是因為實際應用中會出現各種各樣的場景,盡管都是諧振,但是表現各不相同。
先來思考下這么幾個問題:
電路中不必要的LC串聯諧振要絕對杜絕嗎?
MOS管G極經常串聯一個小電阻,說是可以抑制振蕩,啥原理呢?這個電阻阻值怎么取呢?
電源上面加上磁珠,結果紋波變大了,只能換0Ω電阻來解決嗎?有沒有其它的解決方法?
這幾個問題,如果你明白了LC串聯諧振的分析方法,那么自然都不在話下了。
LC串聯諧振電路
盡管LC串聯諧振電路非常簡單,我們還是來看下,這樣一步一步深入會更好的理解。
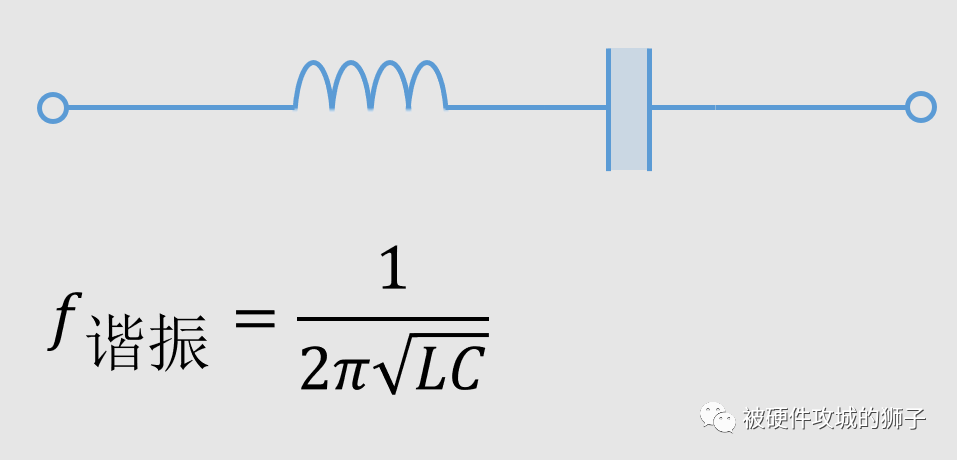
一個電感和一個電容串聯,在某個特定的頻率,就會發生諧振,這個頻率就是諧振頻率。串聯諧振電路有如下特點:
諧振時整個電路阻抗呈電阻性,阻抗最小,電流達到最大;
諧振時電感和電容兩端的電壓達到最大。
上面這些理論都是非常基礎的,就不贅述。實際電路的場景要遠比這個要復雜,搞清楚那些才是我們的目的。那么我們下面就來結合具體的場景。
LC濾波器
LC濾波器經常用,但有一個比較坑的問題就是,有時候使用LC濾波器之后,效果反而更差了,還不如不用。
原因我們當然可以說是在噪聲在此處諧振啦,噪聲被放大了之類的。曾經的我也會這么說原因,不過并不是真的明白,對于這種會起反效果的東西,我會懼怕,會擔心它出問題。這種懼怕,來源于對未知的恐懼,因為沒有懂。現在下面來具體分析下
首先,我們需要明白,噪聲是如何被放大的?也就是說輸出比輸入幅度要大?
先來看最簡單的模型,也就是理想器件模型的情況。
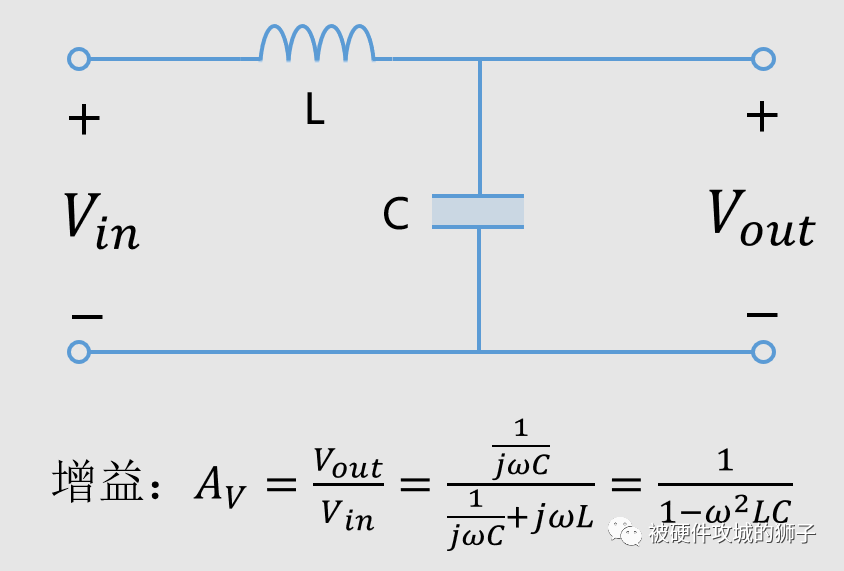
我們列出輸出與輸入的比值,也就是增益,如果增益大于1,那么說明被放大了。很容易列出增益的公式,我們畫下這個曲線。
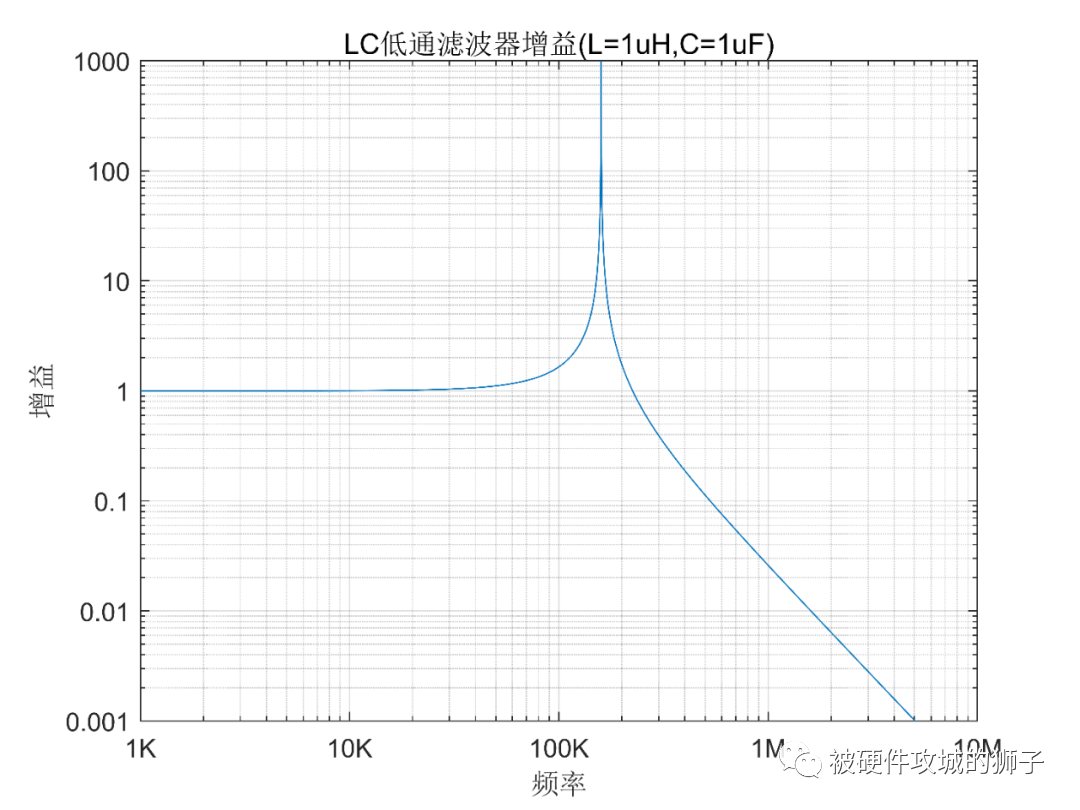
上圖的曲線,是1uH電感,1uF電容的增益。可以看到,在低頻時,增益基本就是1,也就是不放大不衰減。而在諧振頻率處,有一個非常高的尖峰,因為這里設定的器件為理想器件,所理論上尖峰為窮大,諧振頻率旁邊的增益也是非常高的,而在頻率比較高的時候,隨著頻率的升高,增益下降,也就是衰減了輸入信號。
如果我們能把諧振頻率處的增益降到0.707左右,那就是完美的低通濾波器了。很顯然,電感和電容都是非耗能器件,沒有電阻器件的引入,在諧振頻率處,增益總是等于無窮大的。我們從增益Av的公式就可以得出來,因為諧振頻率時的分母為0。
幸運的是,我們的濾波電路總是要接負載的,我們把信號濾波之后總是要給負載用的,接入了負載,那增益又不一樣了。
不同負載的LC濾波器
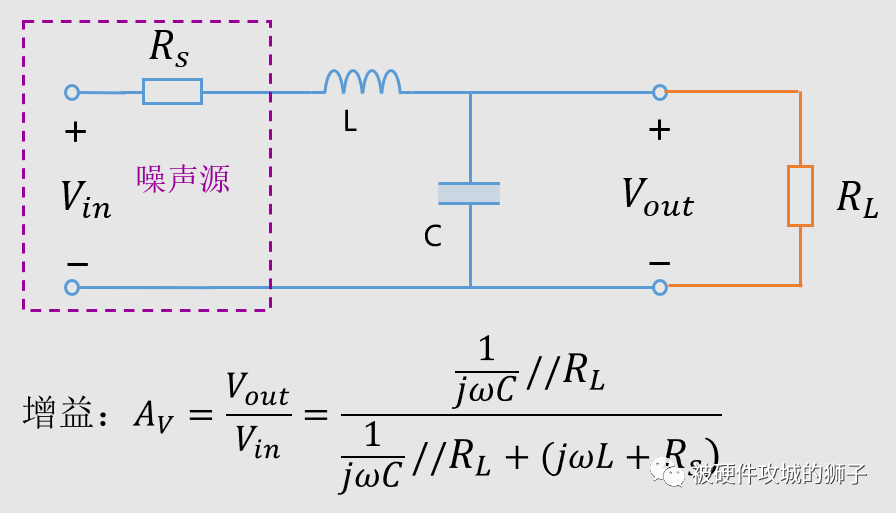
現實中的電路各種各樣,負載的阻抗也就差別很大了,下面是加入負載的模型。
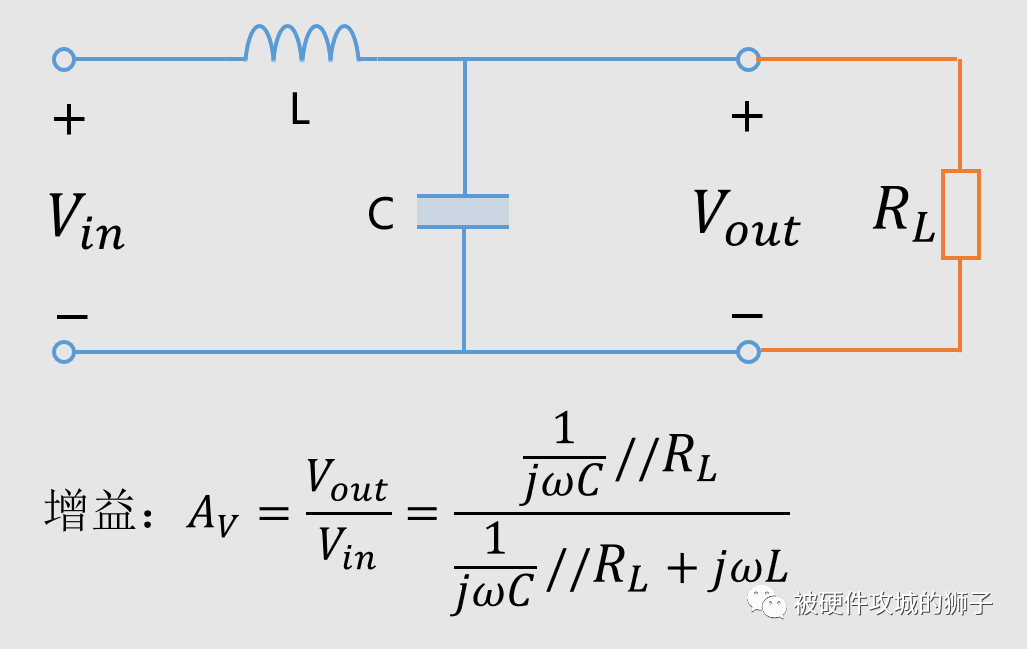
我們看看負載是1Ω,10Ω,100Ω的增益曲線,如下圖:
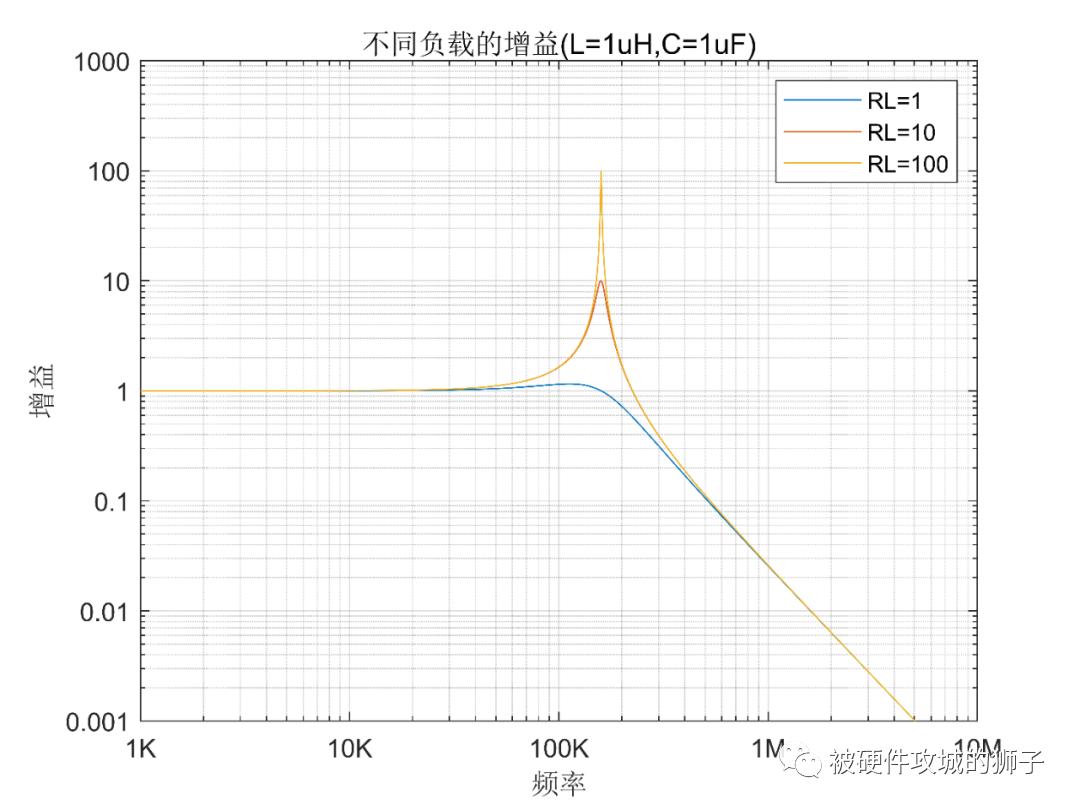
我們可以看到,負載電阻越小,諧振處的增益越小,諧振引起的噪聲變大越不會發生。當然了,實際電路中的負載各種各樣,有低阻的,有高阻的。相對來說,低阻負載的更不容易發生加入濾波器效果更差的事情。因此,如果你發現同樣的LC濾波器,加入不同的電路,有的效果好,有的效果變差,很有可能就是因為負載的不同。
所以說,負載阻抗越低,越不容易產生尖峰,也就是說不容易惡化。
噪聲源內阻的影響
除了負載阻抗的影響,還有噪聲源內阻的影響,實際的噪聲信號肯定是有一定的內阻的。根據內阻的不同,我們構建下面的模型,加入內阻的參量。
分別畫出Rs=0.1Ω,Rs=1Ω,Rs=10Ω的情況,為了排除負載電阻的影響,寧其為高阻態,統一RL=1MΩ。
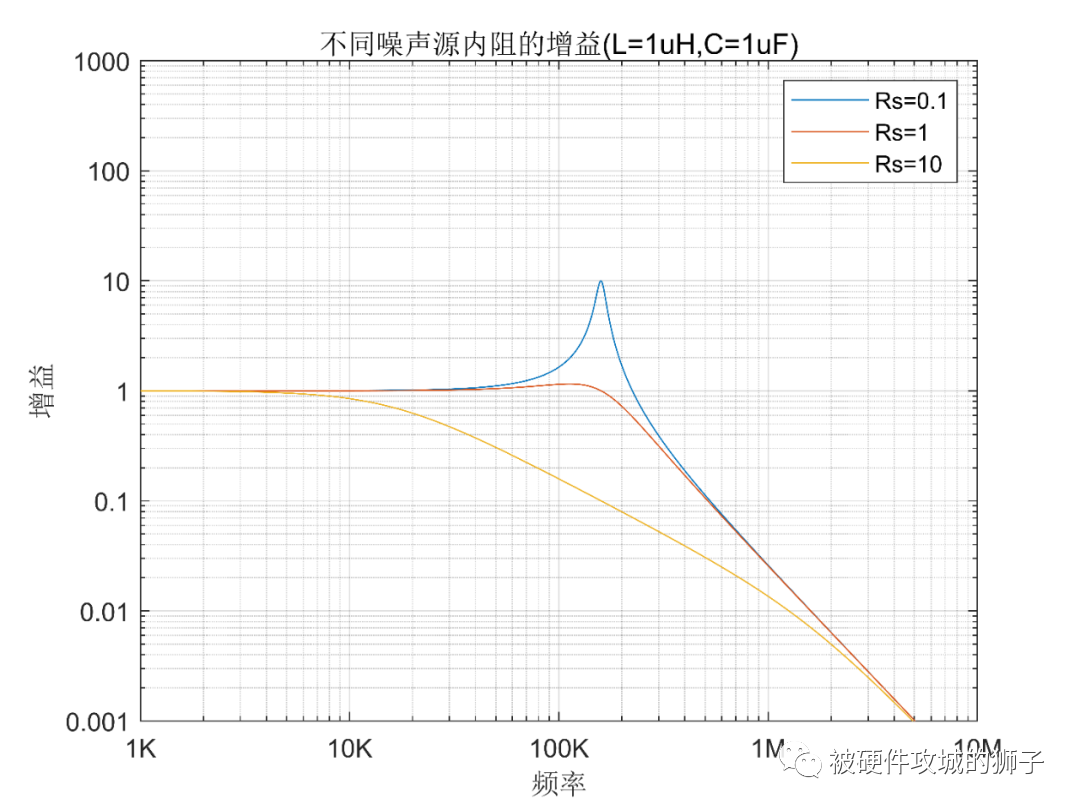
可以看到,內阻越大,越不容易產生尖峰,也就是說不容易惡化,反之,內阻越小,越容易惡化。
L、C的值的影響
除了內阻和負載大小,電感和電容值的大小有沒有影響呢?
電容變化:電容分別為1uF,10uF,100uF,內阻,負載,電感都為Rs=0.1,RL=1MΩ,L=1uH。
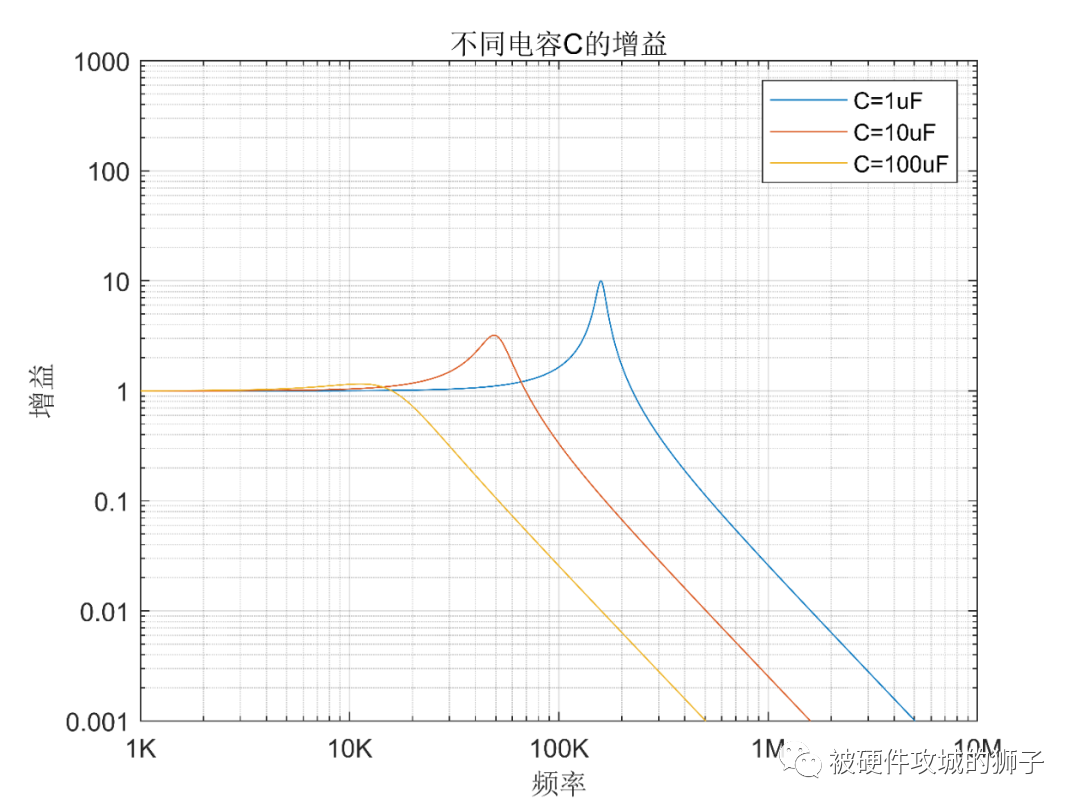
可以看到,電容增大,尖峰變小,也就是說,在遇到諧振引起噪聲增大的情況,可以嘗試增大電容是可以降低噪聲。不過需要注意,尖峰變小,只是說最高點變小了,但是引起了諧振頻率降低,新的諧振點可能還是要比原來的增益更高,也就是說如果噪聲正好是這個頻率段,那么改變之后效果變更差了。當然了,如果我們加更大的電容,即使是諧振點都沒有放大作用,比如如果電容加到100uF,整個頻段基本都沒有放大作用了。
實際電路具體加到多大的電容,完全不會出現尖峰呢?這個跟信號源內阻Rs,負載阻抗RL,電感值L都有關系。實際上,如果內阻Rs從0.1提升到1,電容不用增大到100uF,即使是原來的1uf也不會有尖峰,曲線就不畫了。
電感變化:電感分別為0.01uH,0.1uH,1uH,內阻,負載,電容都為Rs=0.1,RL=1MΩ,C=1uF

可以看到,減小電感,可以降低尖峰的高度。我們如果繼續減小電感到0.01uH,尖峰也會消失。同樣的,電感變化會造成諧振頻率移動,具體是使噪聲變大還是變小也是要依情況而定,與內阻,負載,電容都有關系。
總的來說,大部分電路增大電容,或者減小電感,都可以降低尖峰。如果LC濾波器用于電源濾波發生噪聲變大,可以增大電容,或者減少電感。
這里之所以說大部分電路,是因為如果滿足一定的Rs,RL的條件,可能結果是相反的,這個可以自己修改Matlab代碼(后文分享出來)里面的參量,執行下就知道了。
MOS管G極串聯電阻如何抑制諧振
有了以上的基礎,我們來看實際的問題:MOS管G極串聯電阻如何抑制諧振?
這個問題,我們首先要明白,問題是如何產生的,即為什么會振蕩?其實通過前面的鋪墊,也就很明白了。
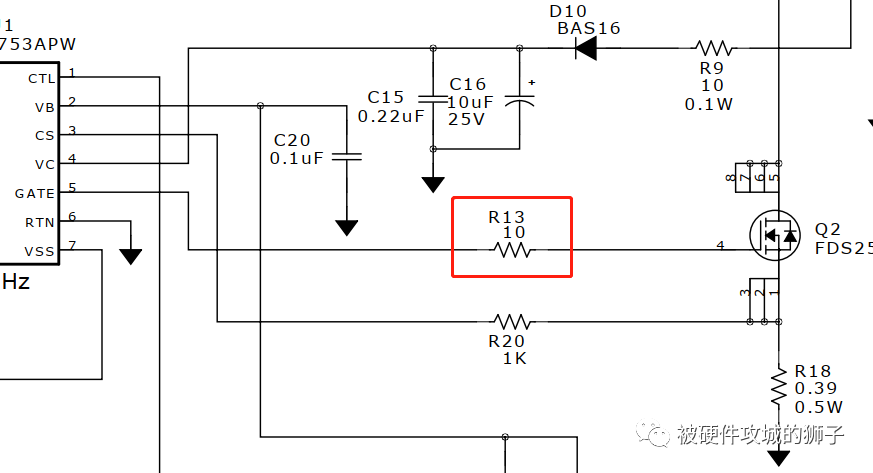
這個是典型的MOS管驅動電路,串聯了10Ω電阻。
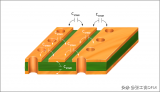
盡管從電路圖上看去,上面既沒有電感,也沒有電容。但實際上是,我們PCB總要將線從驅動芯片拉到MOS管,我查了一下,線寬12mil,長度10mm的走線寄生電感是9.17nH。實際電路中10mm走線太正常了,所以寄生電感肯定是存在的。
電感有了,電容呢?功率MOS管都有輸入電容存在,并且還不小,小的幾百pF,大點的幾nF。我們只是為了說明道理,那取電容1nF吧。
一般來說,左邊驅動管子發出開關信號,它的內阻一般不會很低,盡管現在不知道它到底是多大,那就按照比較惡劣的情況來看,就讓Rs=0.1Ω。
那么負載電阻是多大呢?負載是MOS管,那阻抗就很大了,就取RL=1MΩ。
看看現在的等效電路:
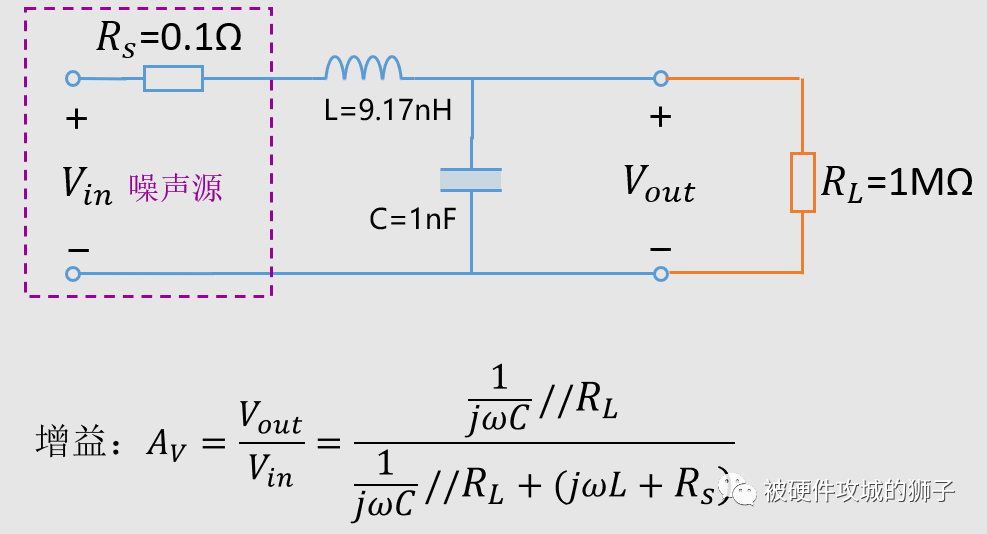
從前面內容知道,源內阻越小,負載阻抗越大,就越容易產生諧振尖峰。我們畫出此時曲線。
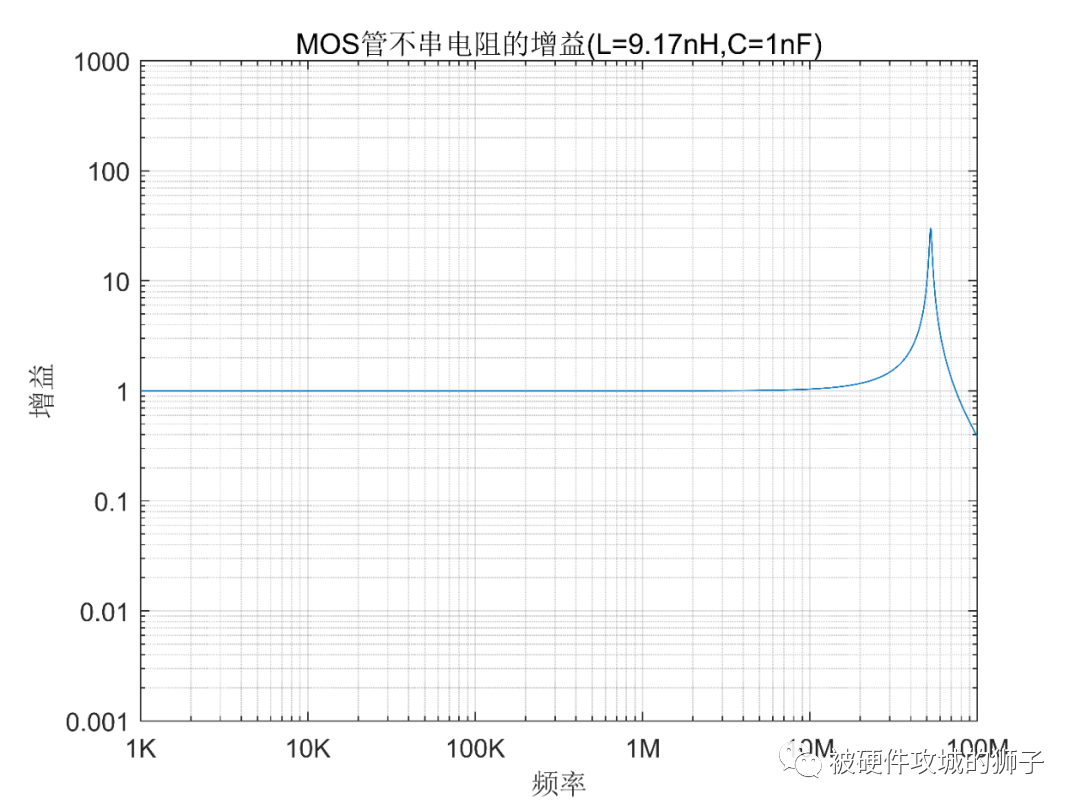
可以看到,諧振頻率52Mhz處增益達到了好幾十倍。而MOS管驅動信號可以看作是一個階躍信號,頻率分量非常豐富,肯定有52Mhz附近的頻率。
所以說確實會發生諧振。
現在分別串聯1Ω,10Ω,100Ω電阻,這個電阻可以等效到內阻里面去,相當于等效電路變成了Rs=1.1Ω,Rs=10.1Ω,Rs=100.1Ω,其它參數不變。我們再看看曲線。
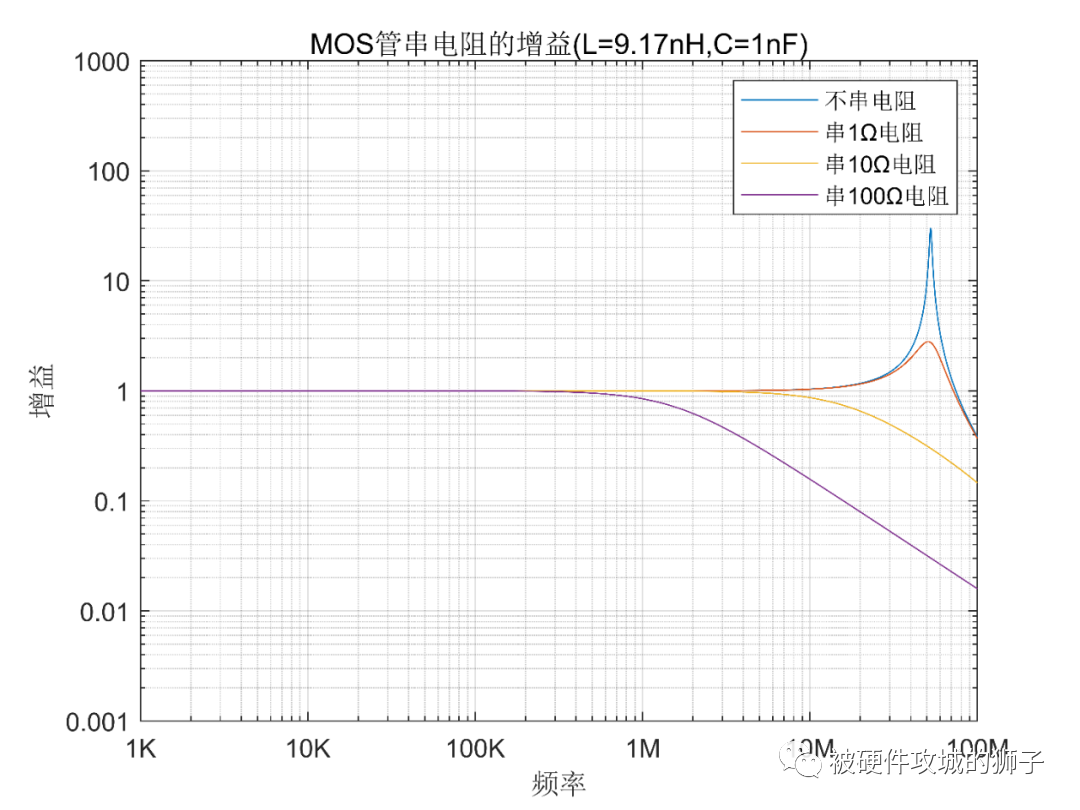
可以看到,串聯1Ω電阻,還是放大,最大到3倍,說明電阻稍小。而10Ω電阻就能完全消除振蕩了。100Ω電阻也能完全消除振蕩,但是其截止頻率更低,會造成驅動信號的高頻分量丟失,最終上升沿變緩,也就是MOS管開啟的時間變長。
相信到這里,對于這個串聯電阻的作用,已經怎么取值應該就比較清楚了。G極走線越長,寄生電感越大,越容易引起問題,電阻就要選得更大些。
審核編輯 :李倩
-
諧振電路
+關注
關注
11文章
165瀏覽量
26975 -
Q值
+關注
關注
1文章
22瀏覽量
12244 -
寄生電感
+關注
關注
1文章
156瀏覽量
14604
原文標題:引言
文章出處:【微信號:被硬件攻城的獅子,微信公眾號:被硬件攻城的獅子】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
如何通過等效串聯電阻(ESR)和等效串聯電感(ESL)來優化熱回路布局設計
用示波器探頭來測試電感的飽和電流的方法
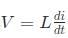
合金電阻的寄生電感及其影響
MOS管寄生參數的定義與分類
如何選擇合適的電感器來匹配感性負載?
MOS管寄生參數的影響
普通探頭和差分探頭寄生電容對測試波形的影響
系統寄生參數對SiC器件開關的影響分析

為什么BUCK芯片的電感電流在上下峰值處出現抬升和跌落?
什么是寄生電感?如何計算過孔的寄生電感?

寄生電感到底是什么?如何計算過孔的寄生電感?
電感的作用和工作原理 電感充放電原理
PCB寄生電容的影響 PCB寄生電容計算 PCB寄生電容怎么消除




 寄生電感怎么來的
寄生電感怎么來的










評論