S分段C覆蓋并行加法器
第一章:設計
經過學習,行波進位加法器RCA和超前進位加法器CLA后。
自己動手設計一個八位二進制加法器。
經過分析,二進制加法,可以分成三種情況。
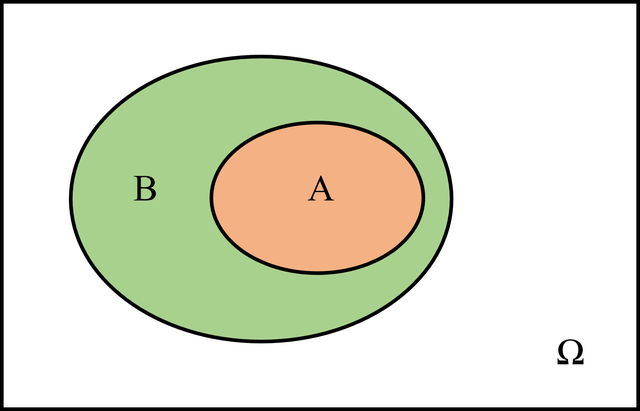
A:最特殊情況,兩個八位二進制數的相同位,不同時為1,這樣就不會產生進位。
B:特殊情況,兩個數相加,產生進位C,但是更高一位的S是0。
Ω:普通情況,產生進位后,需要繼續(xù)進位的情況。
對于A:8個半加器就可以輸出正確答案。
對于B:8個半加器輸出S和C,用Cn和Sn+1異或,就可以輸出正確答案。
對于Ω:就需要發(fā)現規(guī)律。
當低位C向高位S進位時,有兩種情況。
S=0,則直接進位。
S=1,則本位異或為0,進位C向更高位,繼續(xù)進位,直到遇見S=0。
所以需要一種靈活的電路,當S=1時,能夠把低位C搬運到高位去。
把S組成的0111結構稱為段,C=0時,異或出結果0111。C=1時,異或出結果1000。進位將是向段進位的。
下圖就是最終電路設計。使用八個串聯的傳輸門,由各位的S控制通斷,靈活分配進位C。
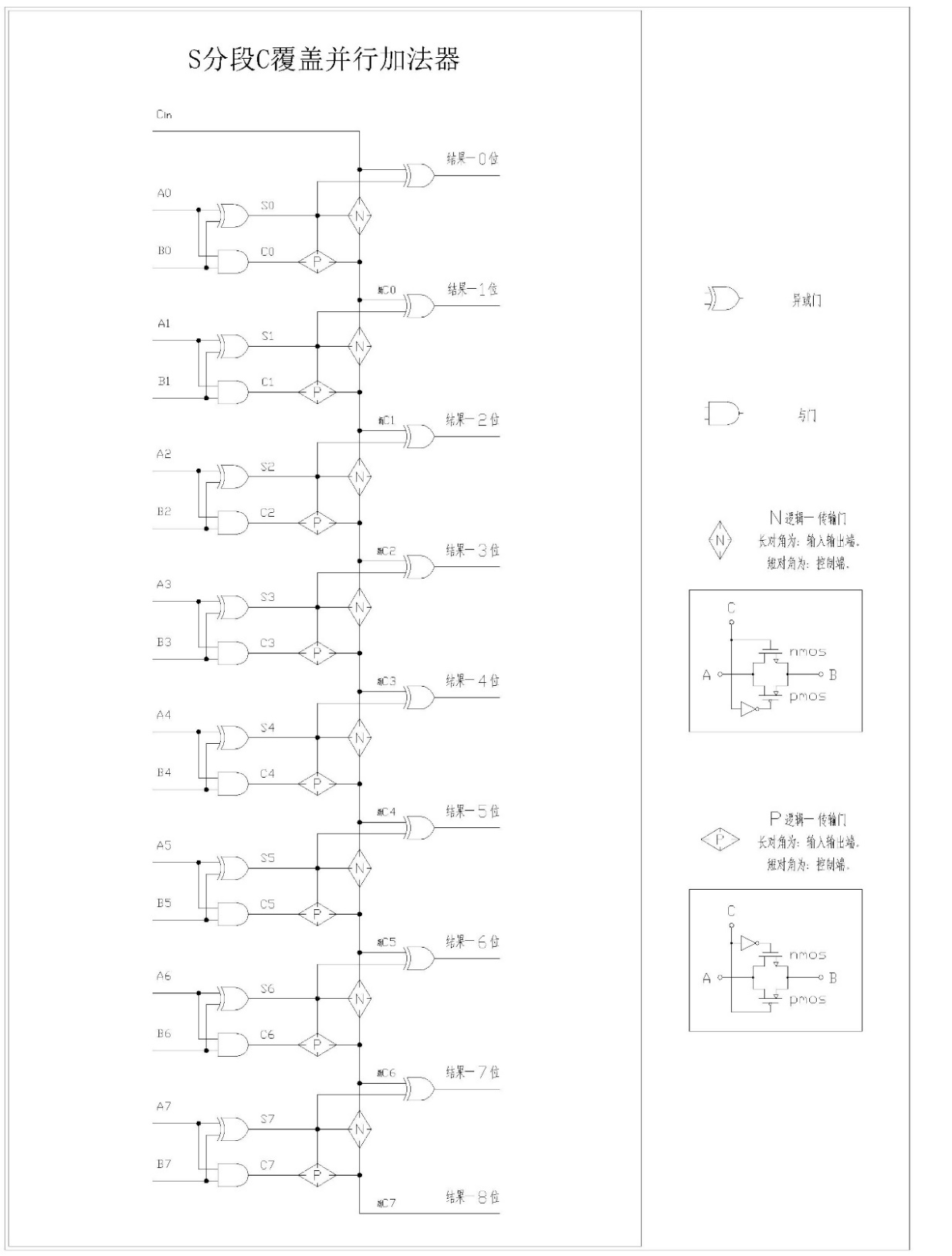
由于低位C為1,向高位進位,S為0時,N邏輯傳輸門截止,P邏輯傳輸門導通,本位C可以通過P邏輯傳輸門進入到下級異或門參與運算得到運算結果;當S為1時,N邏輯傳輸門導通,P邏輯傳輸門截止,此時本位C無法參與下級異或門運算,低位C則可以通過N邏輯傳輸門進入下級異或門參與運算,直到遇到S=0時停止。低位C和段內S異或運算,得到計算結果。依次從低位到高位看S的值,從S為1開始到S為0,稱之為一段,此段內的所有C都會被低位C(本級S為1的上一級C)“覆蓋”,結果為新C。當S出現極端情況0111...0結構的段時,最低位的C覆蓋所有高位C參與運算。
計算機是如何計算的(視頻有利于理解設計)
1探索篇
2設計篇
3優(yōu)化篇
經過Proteus 7.8的驗證,設計的加法器,能夠計算出正確結果。
使用虛擬示波器測出RCA和SCA(本設計)的延遲時間:
| 加法器延遲 | 4位 | 8位 | 16位 | 32位 |
| RCA | 1.3微秒 | 1.64微秒 | 2.4微秒 | 3.8微秒 |
| SCA | 1.4微秒 | 1.4微秒 | 1.4微秒 | 1.4微秒 |
RCA:
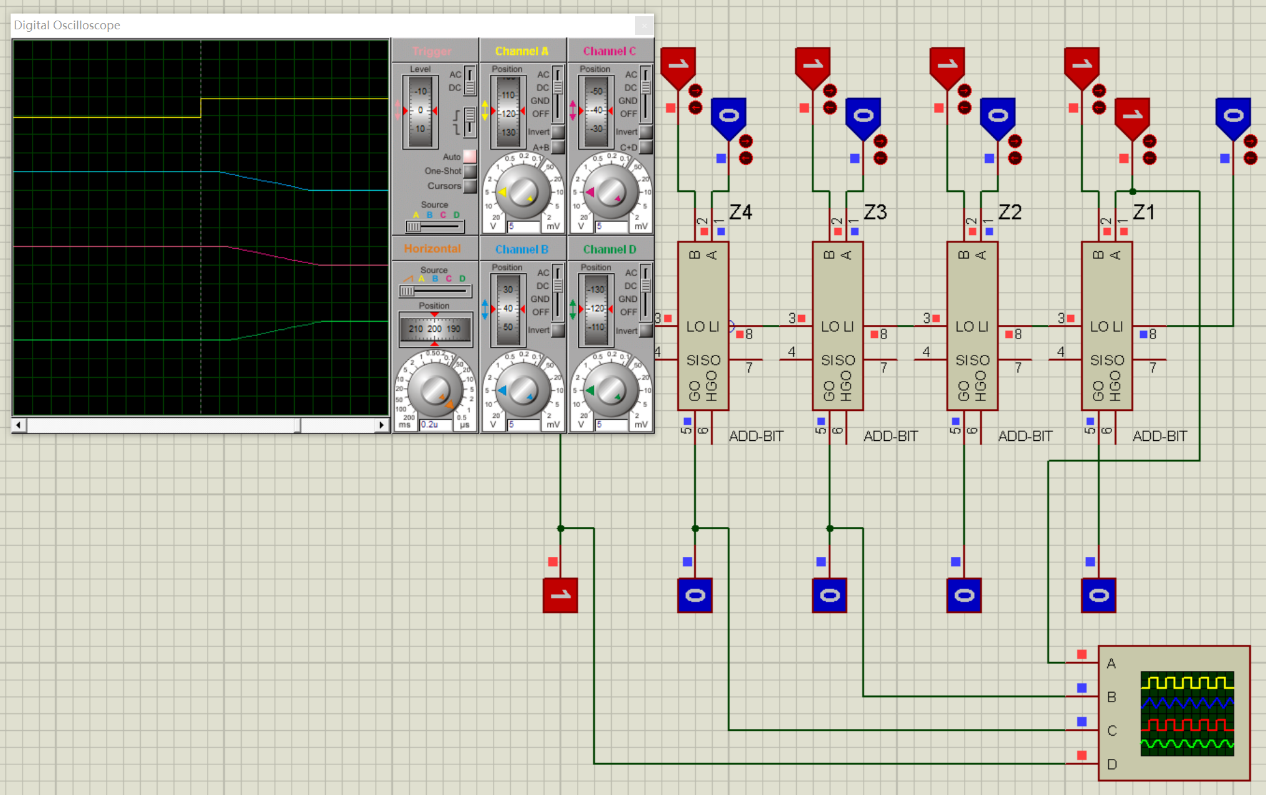
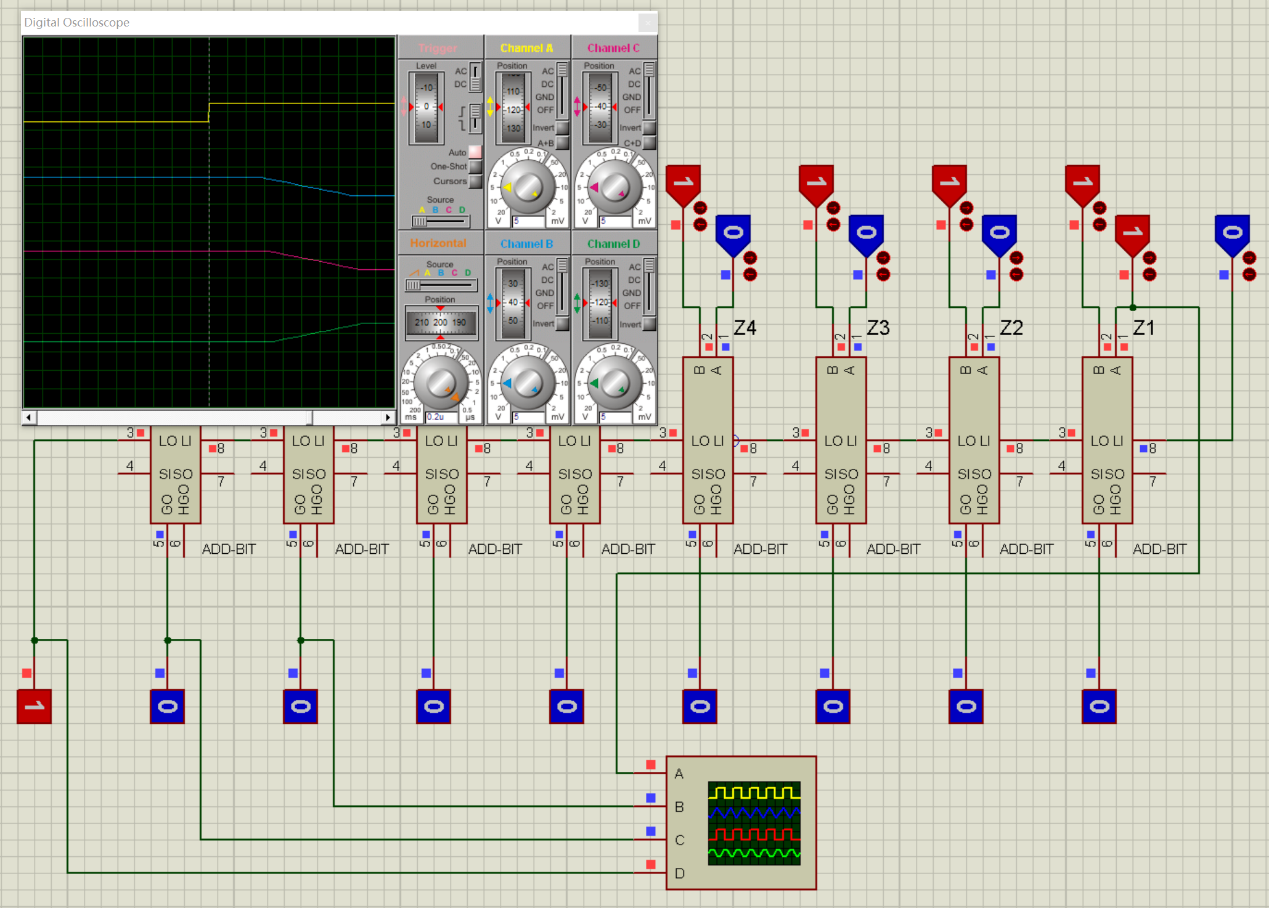
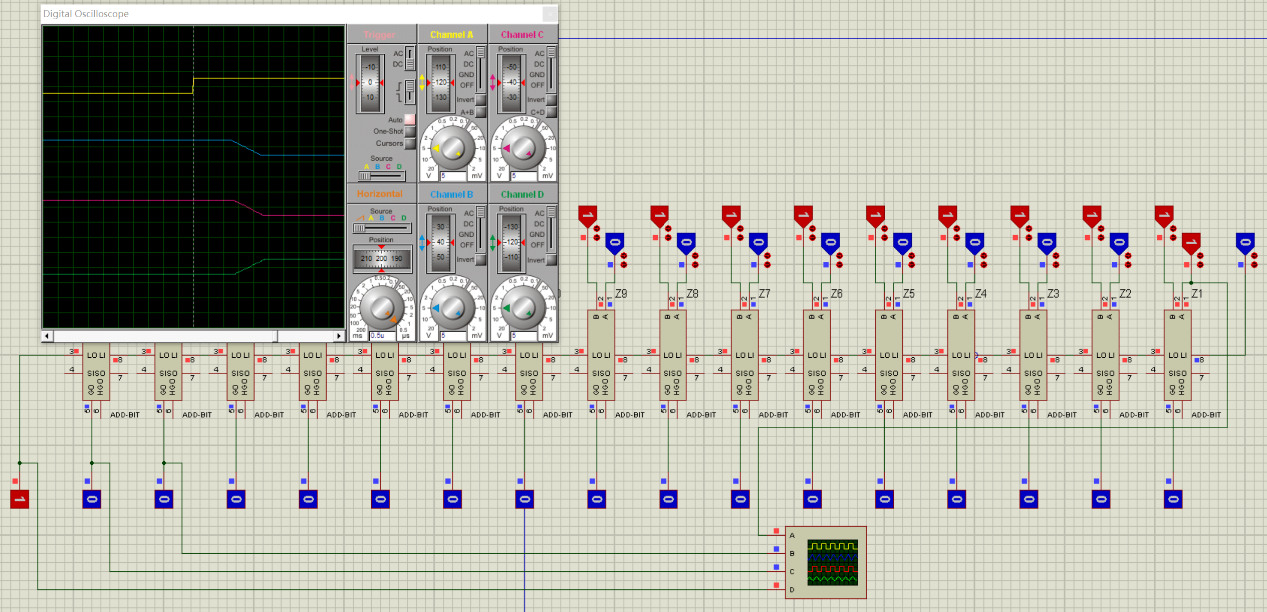
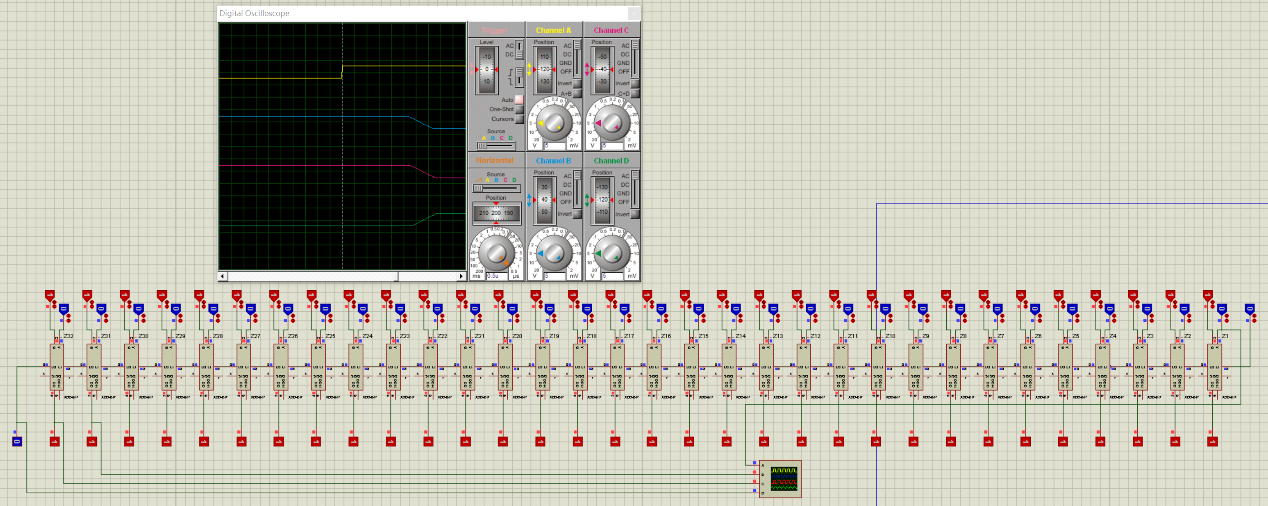
SCA:
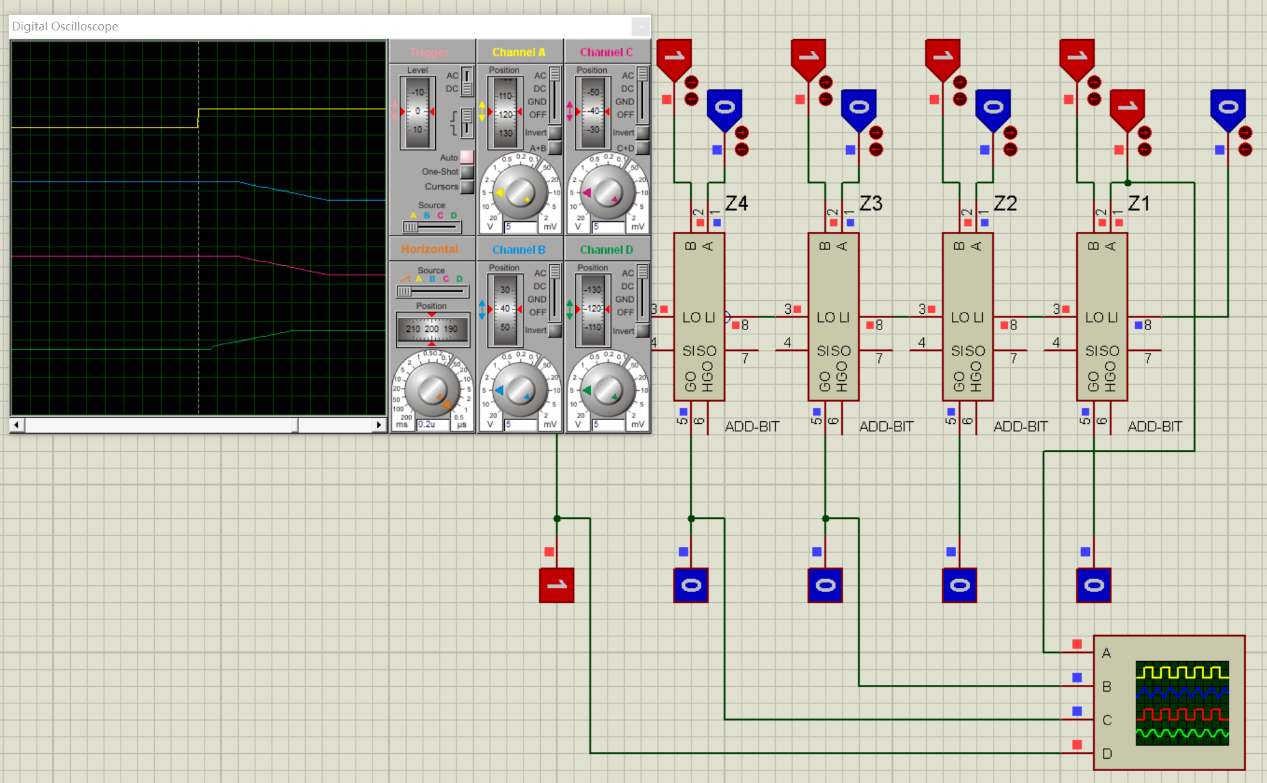
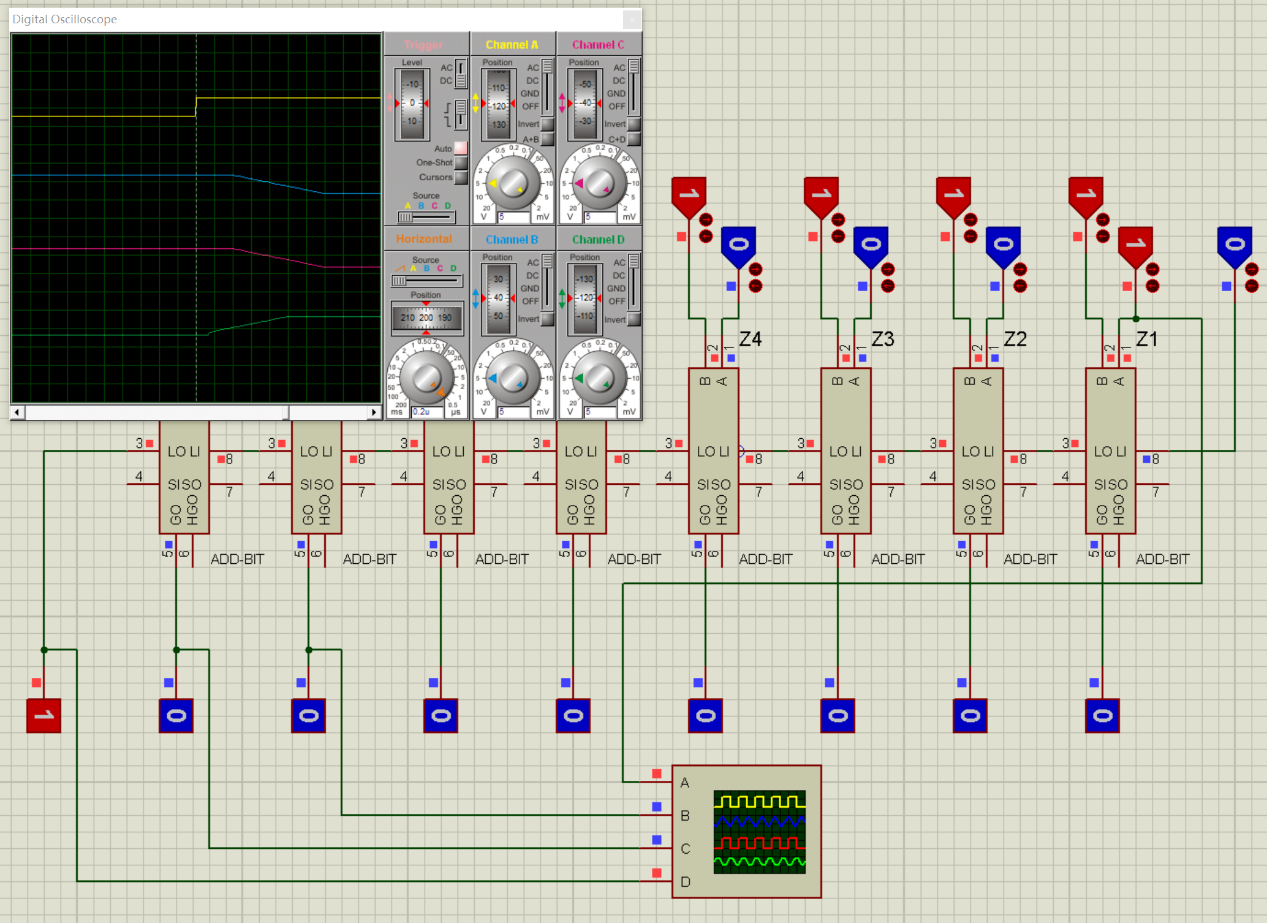
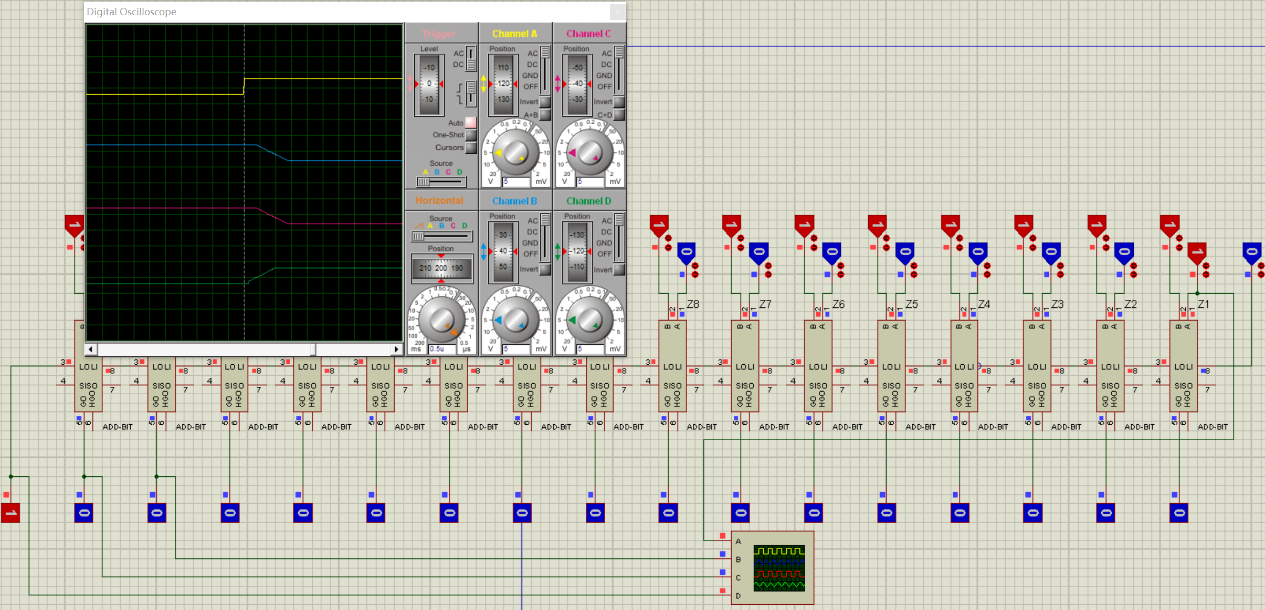
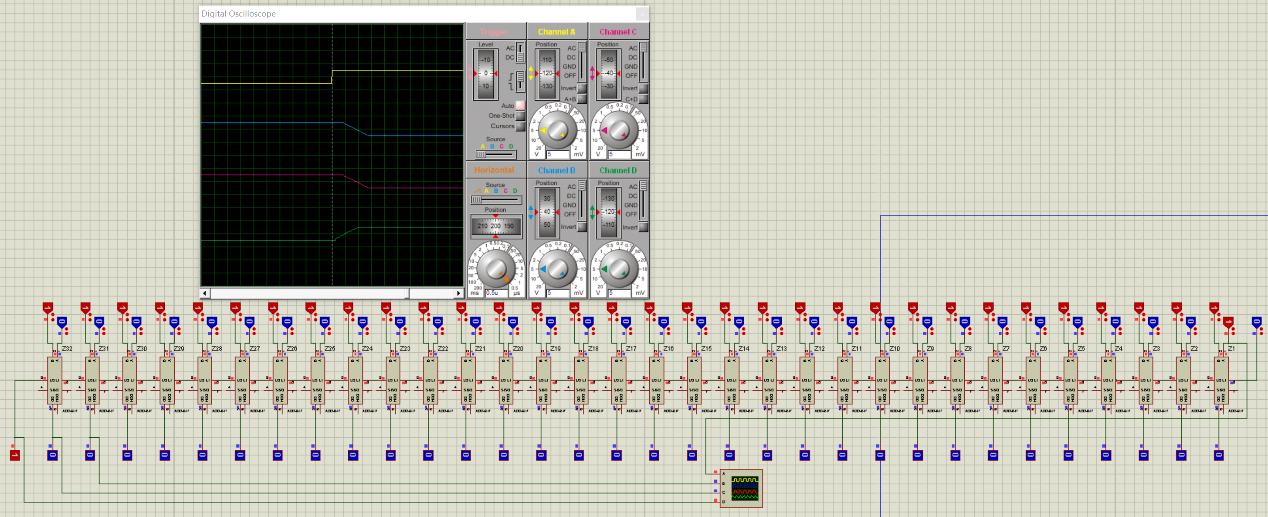
以上是,Proteus7.8的測試結果
第三章:multisim驗證。示波器測延遲
使用multisim 14的虛擬示波器測出RCA和SCA(本設計)的延遲時間:
| 加法器延遲 | 4位 | 8位 | 16位 |
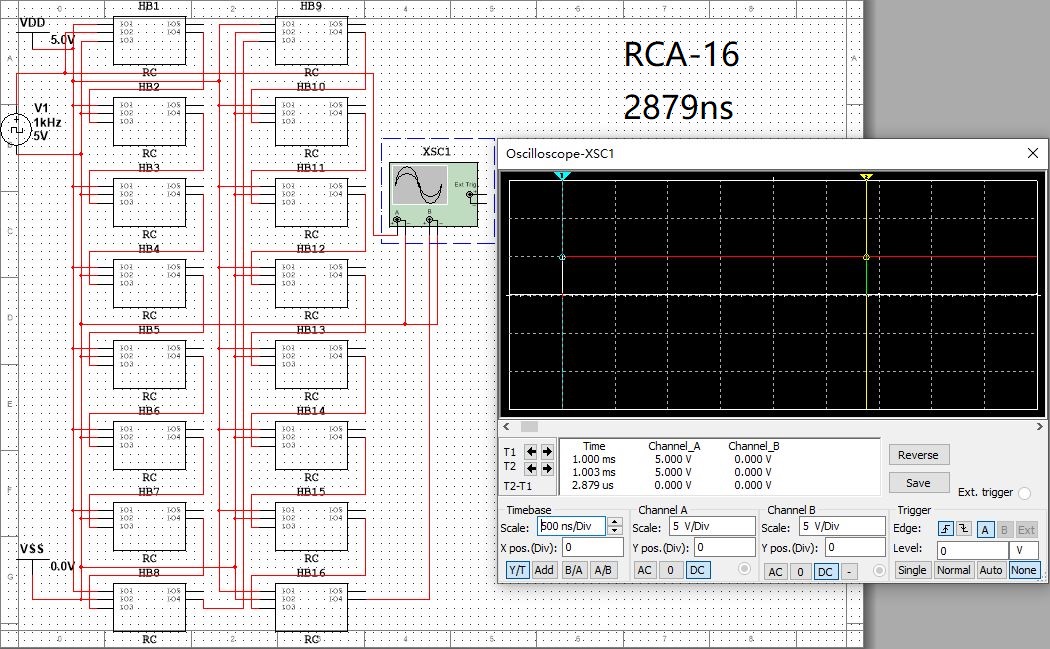
| RCA | 723納秒 | 1439納秒 | 2879納秒 |
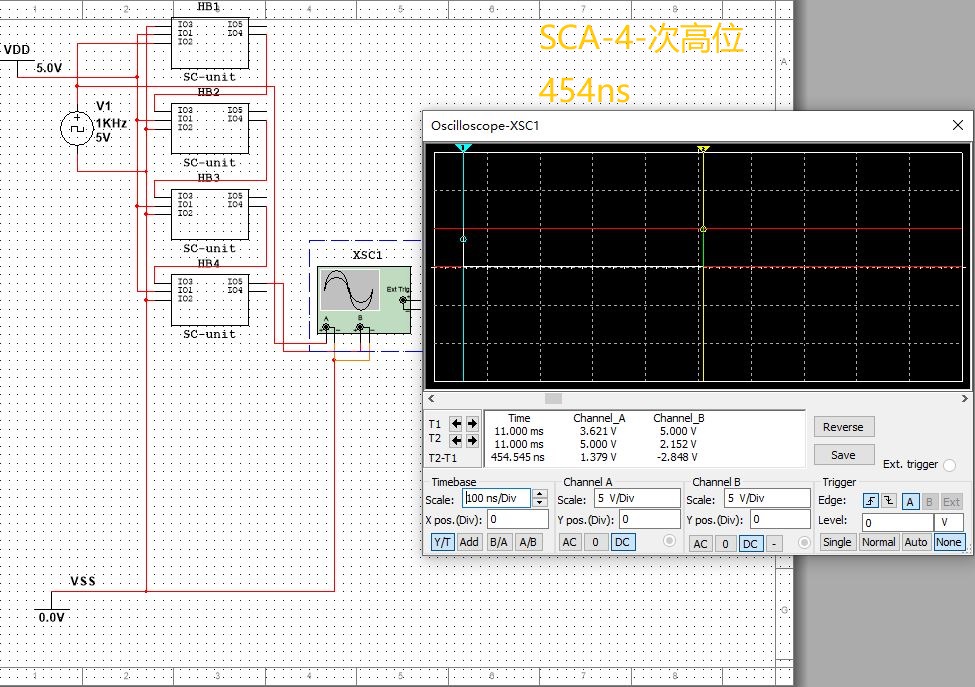
| SCA | 454納秒 | 454納秒 | 454納秒 |
RCA:
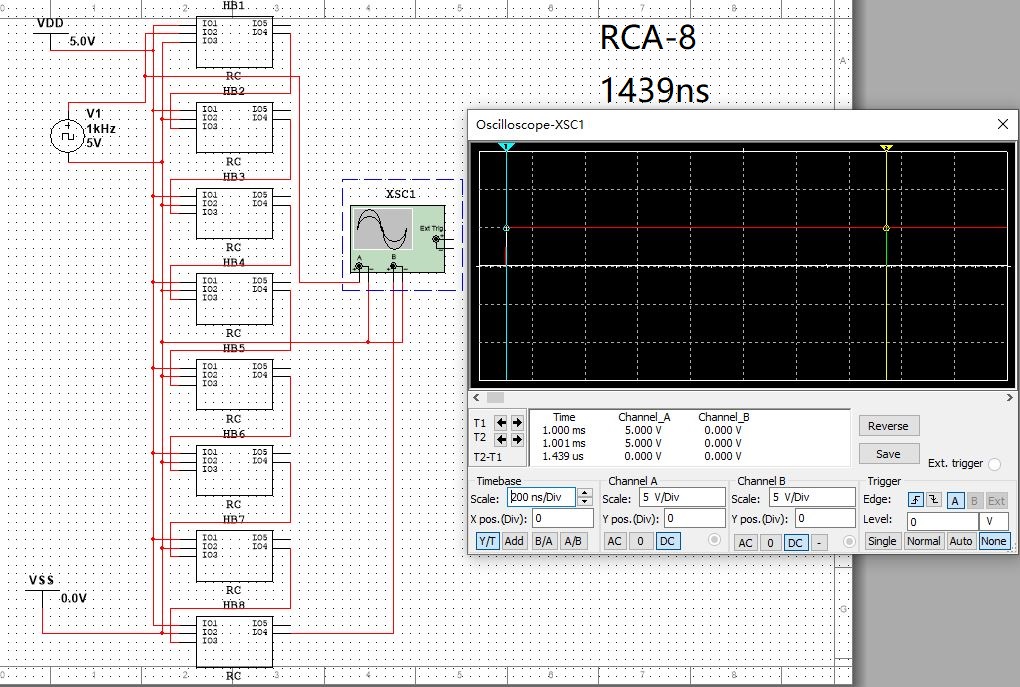
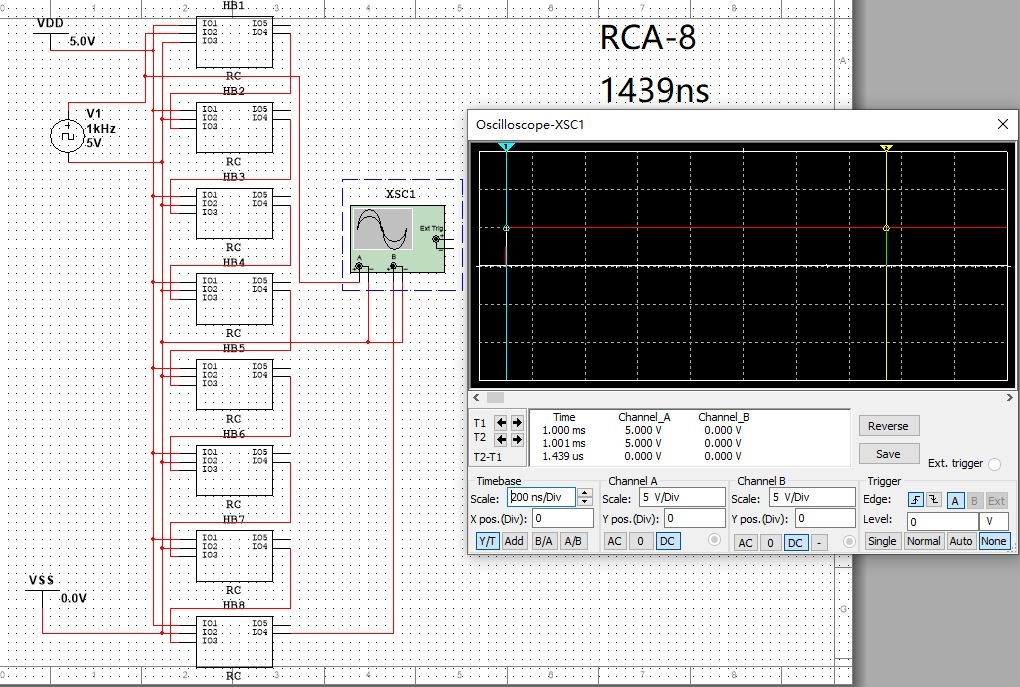
SCA:
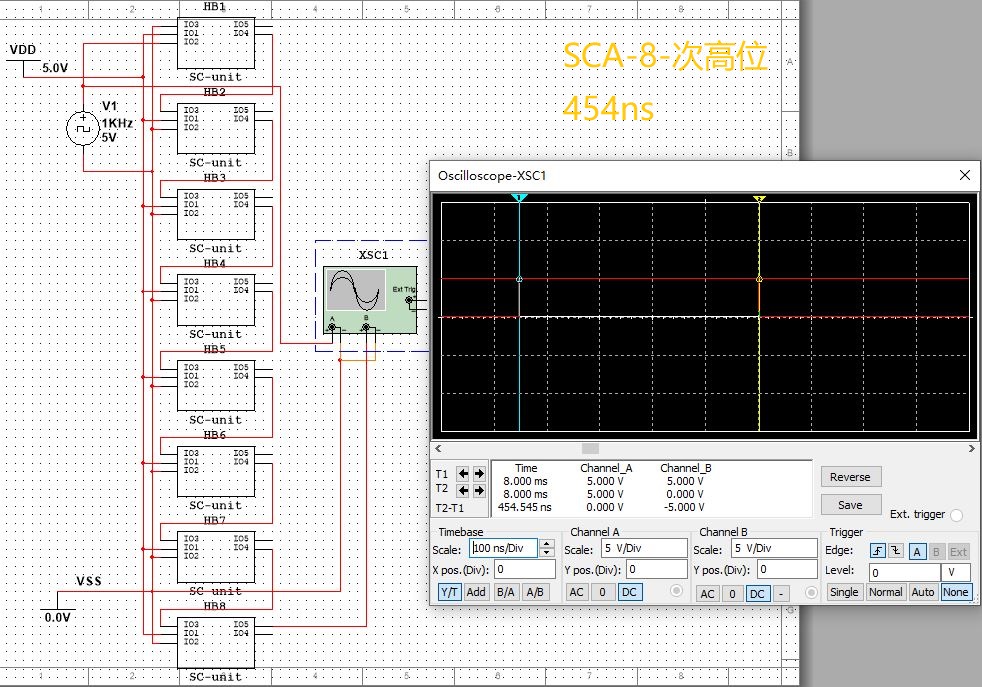
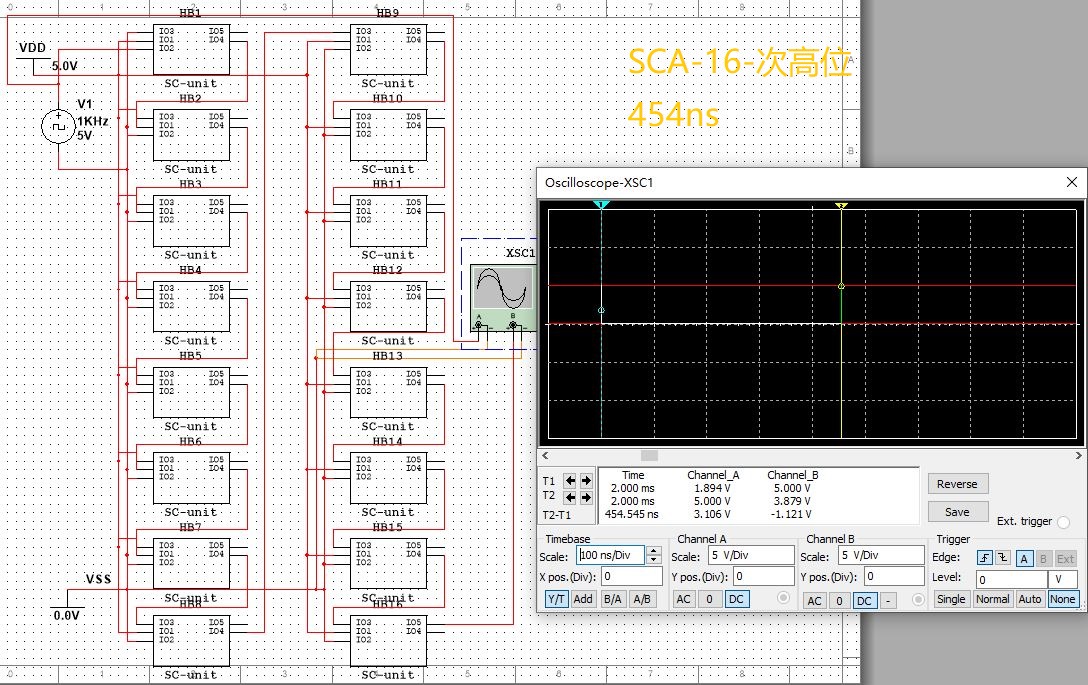
以上是,multisim 14的測試結果
第四章:PCB實物驗證延遲
由于模擬軟件的延遲測試,僅僅只能參考。
計劃利用74HC系列芯片,制作出RCA和SCA(本設計)的PCB電路板。使用示波器對兩種加法器進行對比。
SCA-4示波器測延遲:
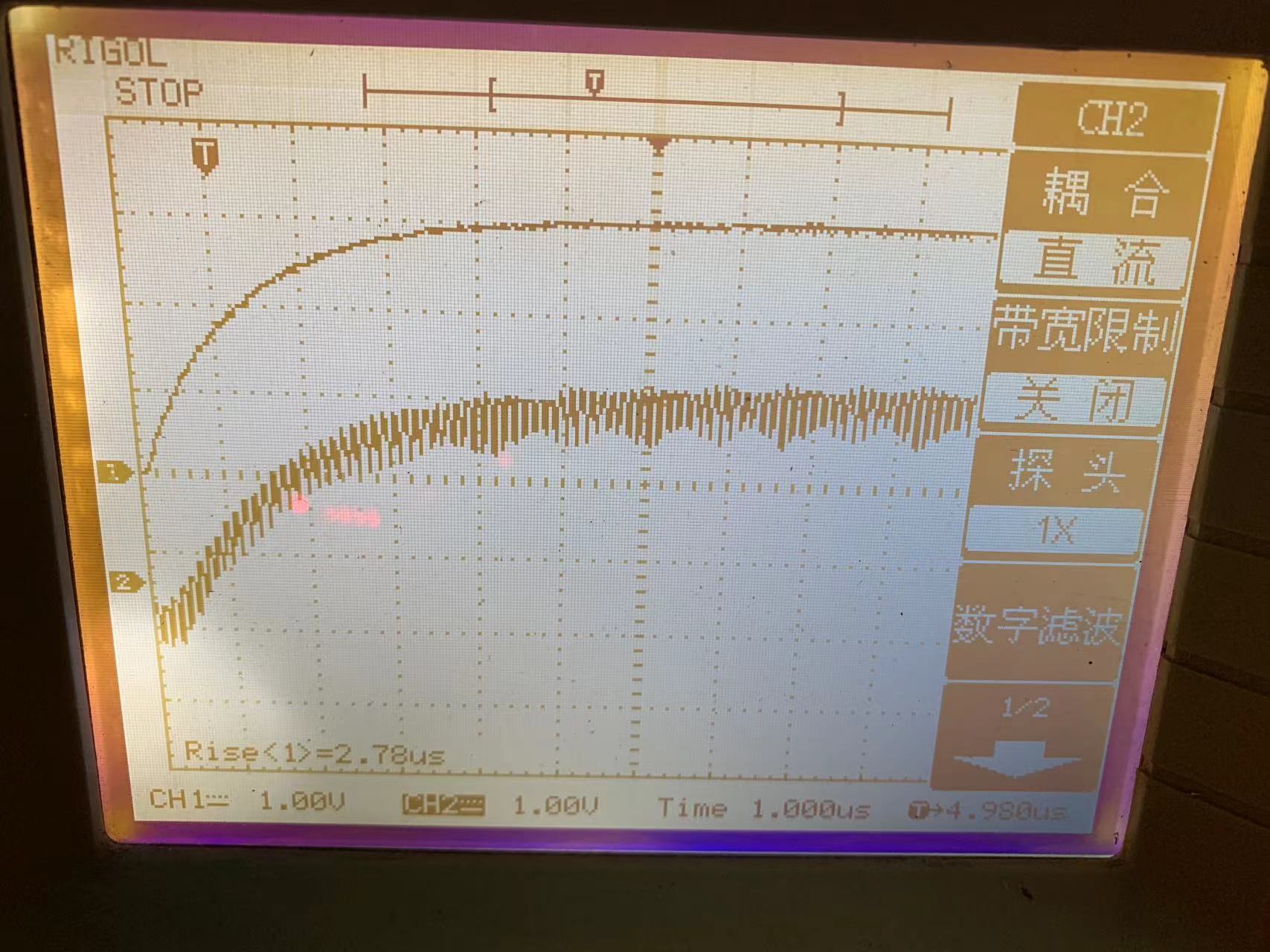
RCA-4示波器測延遲:
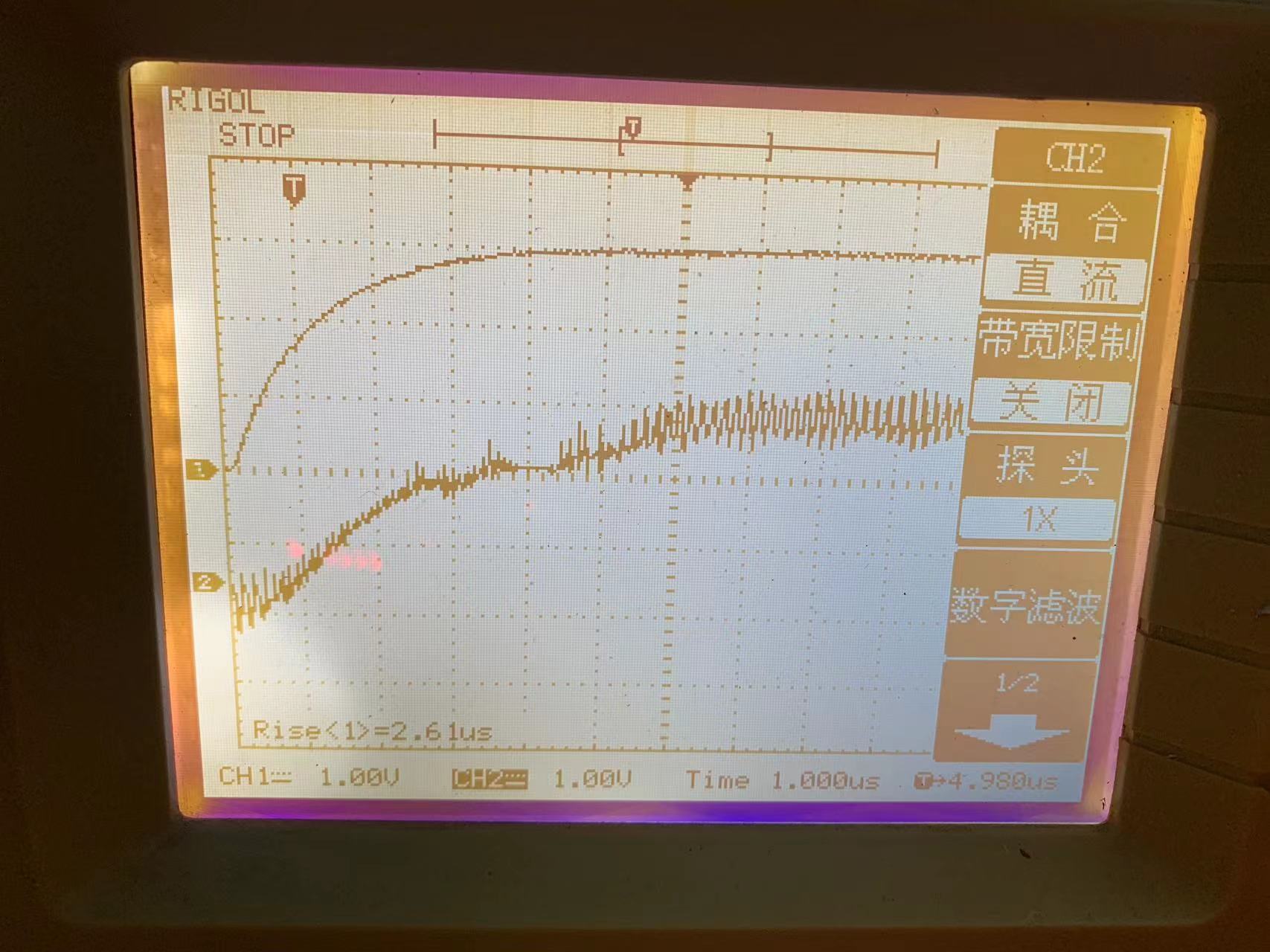
實物圖:

中間兩行是輸入開關,為A1-4,B1-4D的輸入,SW9為Cin。
上半部分的5顆芯片,組成RCA-4,
下半部分的6顆芯片,組成SCA-4。LED輸出結果。
開關向右波動為3V,開關向左波動為0V。
圖中A為1111,B為0000。輸出LED顯示1111。
結果正確。
已經試過所有的4位加法,全部正確。
審核編輯:湯梓紅
-
電路設計
+關注
關注
6715文章
2549瀏覽量
215495 -
Proteus
+關注
關注
79文章
1692瀏覽量
108929 -
加法器
+關注
關注
6文章
183瀏覽量
30879
發(fā)布評論請先 登錄
十進制加法器,十進制加法器工作原理是什么?
FPU加法器的設計與實現
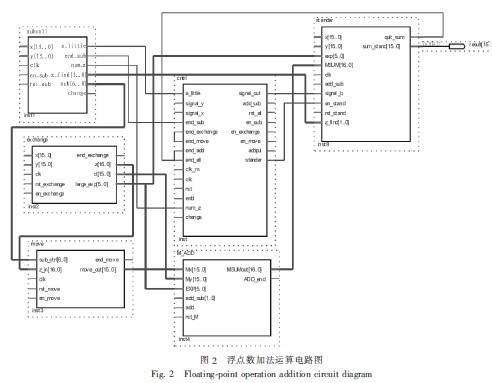
同相加法器電路原理與同相加法器計算
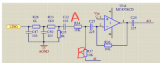
怎么設計一個32位超前進位加法器?
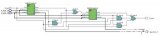
12位加法器的實驗原理和設計及腳本及結果資料說明
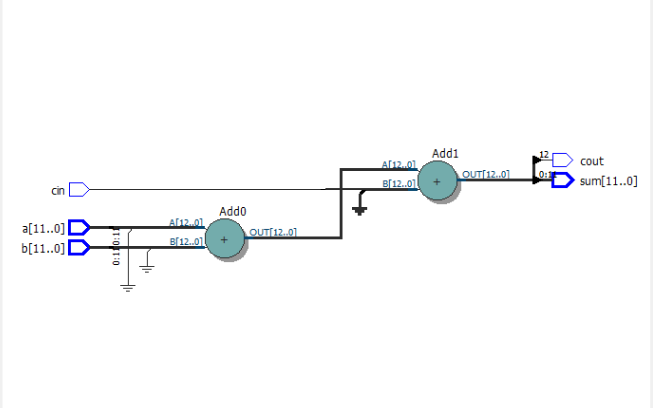






 怎樣測量加法器的速度?器件延遲的時間長度!
怎樣測量加法器的速度?器件延遲的時間長度!













評論