根據自己對慣性導航姿態解算的學習,簡單總結一下自己對慣導解算認識。先畫一張從傳感器數據到最終位姿的過程梳理圖。

01平臺式慣性導航系統和捷聯慣性導航系統
平臺式慣導的系統主體是平臺,平臺始終跟蹤當地的水平面,軸向始終指向東北天方向。利用位于穩定平臺上的加速度計測量載體在導航坐標系下的xyz軸的加速度,積分得到位移速度和位置。 缺點:其體積和重量大,而平臺也是一個高精度、復雜結構的機電控制系統。
捷聯式慣性導航系統 (Strapdown inertial navigation system) Strapdown 具有“捆綁”的意思, 陀螺儀、加速度計與載體“捆綁”。載體的姿態和航向可以用載體坐標系(b系)相對于導航坐標系(n系)的三個轉動角決定。就是說,在捷聯式慣性導航系統中,直接測得的三個方向的加速度是載體坐標系三個軸方向上的,需要用一個捷聯矩陣C將其變換到導航坐標系中來。
02坐標系
運載體中三維空間運動包含六個自由度,既有角運動也有線運動。在地球表面附近,運載體的角運動描述一般以當地水平面和地理北向為參考基準;線運動的描述通常采用地理經度、緯度和高度表示,它是相對于整個地球旋轉橢球體而言。
但是,運載體上慣導系統使用的關系傳感器(陀螺儀和加速度計)從原理上看是相對于慣性空間進行測量的。另外,地球繞其自轉軸相對于慣性空間以常值角速率旋轉,運載體在地球表面位置變化會引起其相對于地心的角速率。
03
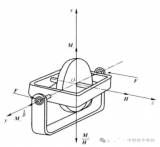
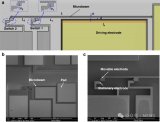
慣性傳感器
以 MEMS 慣性傳感器為例,通過“感觸”地球引力場和自旋角速度(加速度計和陀螺儀)通過數學算法(積分)獲得角速度、加速度、速度、位置等基礎參數。 因為傳感器測量的誤差存在,在積分運算時,勢必將測量誤差引入了積分,隨著時間的累積,積分誤差也一直在累加。因此在整個姿態解算前,對誤差建模分析與補償尤為重要。
誤差來源
對MEMS 慣性傳感器來說,引起誤差的主要原因有: 1) 慣性器件本身結構的不完善和工藝差異 2) 慣性器件內部物理因素變化如溫度、雜散磁場等 3) 外界環境如溫度變化、外界磁場干擾、載體劇烈變化等
誤差模型
根據不同的(確定性和隨機)誤差參數分析,推導出誤差模型(數學公式)。
對確定性誤差參數是可辨識的(這種辨識是指通過一定的標定方法可以補償,基本消除的誤差)。常用六面法借助于轉臺標定加速度和陀螺儀。
不需要轉臺的標定常用 迭代優化方法。`參考文獻:D. Tedaldi, A. Pretto and E. Menegatti, “A Robust and Easy to Implement Method for IMU Calibration without External Equipments”. In: Proceedings of the IEEE International Conference on Robotics andAutomation (ICRA 2014), May 31 - June 7, 2014 Hong Kong, China, Page(s): 3042 - 3049`
對隨機誤差常用 Allan方差分析
04傳感器輸出的原始單位數據直接輸出角度3軸加速度計寄存器讀取到的十六進數據 和 選擇的測量范圍決定加速度數據的測量精度。Eg:加速度計讀到的數字是1000,那么對應的加速度數據是1000/2048=0.49g 因此,利用加速度計測量重力向量在感應軸上的映射。被測加速度的振幅隨感應軸與水平面的夾角α的正弦值的變化而變化,可以推算出三軸的傾斜角度。



利用三角函數計算俯仰和滾轉角

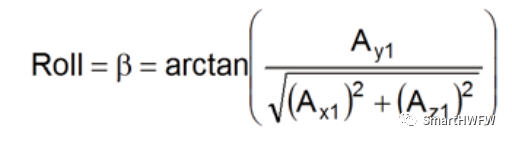
特別要注意:加速度計繞 Z 軸旋轉時,各軸的重力分量不會變化。因此,不用推算 yaw 角解算。一般采用磁力計推算。
3軸陀螺儀從寄存器讀取到的十六進數據 和 選擇的測量范圍決定陀螺數據的測量精度。Eg:當讀取陀螺儀的值是1000,對應的角速度計算如下:32767/2000 =1000/x; 即 x = 1000/16.4(°/s) 因此,利用陀螺儀直接輸出角度時,將需要把角度 °/s 換算成弧度。即:1°/s = π/180 = 57.3rad/s。對3個軸轉動的角速度積分,可以得到角度。
數據融合
通過上述方法直接利用加速度計和陀螺儀是可以輸出角度的。但是往往在具體的應用中加速度計和陀螺儀都表現出不同的特性。
由于加速度易受高頻噪聲干擾,因此算得的姿態角是很不穩定的,不能直接參與控制。陀螺儀對振動不敏感,不產生高頻噪聲,但陀螺儀有零偏、積分出的姿態會飄移。在應用中加速度計對高頻振動噪聲比較敏感,陀螺儀對低頻噪聲敏感。
| 對比項 | 加速度計 | 陀螺儀 |
| 高頻振動噪聲 | 敏感 | 無感 |
| 低頻姿態飄移 | 不飄 | 會飄 |
如上對比,因為加速度和陀螺儀都存在各自的不足之處,因此我們需要引入數據融合(濾波算法)。 常見的濾波算法:DMP直接輸出角度 > 卡爾曼濾波 > 四元數解算 > 清華角度濾波 > 一階互補濾波 在項目中常用:EKF、DCM/Mahoney、Madgwick(基于梯度下降法)等算法
`參考文獻:Madgwick S O H, Harrison A J L, Vaidyanathan R. Estimation of IMU and MARG orientation using a gradient descent algorithm[C]//Rehabilitation Robotics (ICORR), 2011 IEEE International Conference on. IEEE, 2011: 1-7.`
位姿表達
在 AHRS 系統下描述的是載體坐標系的軸系相對于導航坐標系的軸系之間的角度關系(方向)。通常用歐拉角法或者四元數法表達。常用的方法還有:方向余弦矩陣法、等效旋轉矢量法。 在采用歐拉角時需要考慮的問題是:萬向節死鎖 不同的旋轉規則下死鎖的情況不一樣,在Z Y X 的順規下,當pitch角度為90或-90的時候,roll和yaw角度會亂飄,這就是遇到了萬向節的死鎖。
因此,很多做方案的公司都是用四元數表征傳感器的姿態。在這個地方 yaw 角是通過地磁傳感器解算的。地磁傳感器測量的是自身和磁北的角度。北東地坐標系和磁北不是同一個方向。 單位四元數(Unit quaternion)可以用于表示三維空間里的旋轉。四元數表示能夠更方便地給出旋轉的轉軸與旋轉角。
// 繞Y軸旋 eulerAngle.pitch = asinf(2 * q0 * q2 - 2 * q1 * q3) * (180 / PI); // 繞X軸旋轉 eulerAngle.roll = atan2f(2 * q2 * q3 + 2 * q0 * q1, -2 * q1 * q1 - 2 * q2 * q2 + 1) * (180 / PI); // 繞Z軸旋轉 eulerAngle.yaw = atan2f(2 * q1 * q2 + 2 * q0 * q3, -2 * q2 * q2 - 2 * q3 * q3 + 1) * (180 / PI);
05
通過一次二次積分獲得速度和位置
在載體坐標系下通過矩陣轉換到導航坐標系后,加速度計包含的重力加速和運動加速度。積分是只針對運動加速度積分。所以,需要把重力加速度給補償掉。
然后一次積分得到速度,二次積分得到位置。但是積分存在累加誤差,因此在室外的時候通過 GNSS 對速度和位置做修正。
是呢環保局:郭婷
-
傳感器
+關注
關注
2552文章
51362瀏覽量
755696 -
陀螺儀
+關注
關注
44文章
790瀏覽量
98872 -
加速度計
+關注
關注
6文章
704瀏覽量
45957
原文標題:MEMS 慣性傳感器 03 - 慣性導航位姿解算基礎框架
文章出處:【微信號:SmartHWFW,微信公眾號:SmartHWFW】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
淺談慣性導航產品的對齊安裝角度
愛普生(EPSON) 慣性測量單元(IMU)、陀螺儀傳感器等模塊應用領域選型介紹

AGV小車上的慣性導航模塊運用——SGPM02

基于MEMS的慣性測量組合,實現中精度、低成本、高可靠性
【核芯觀察】IMU慣性傳感器上下游產業梳理(二)
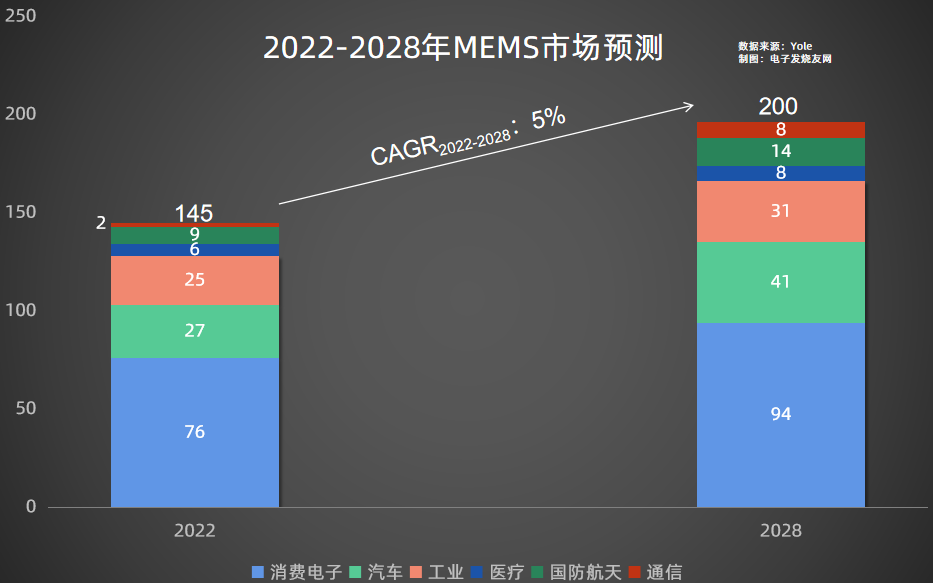
MEMS傳感器細分領域未來方向,關注射頻、慣性和壓力三大應用領域(深度分析)
航天傳感器知識丨慣性敏感器的基本原理及其分類
愛普生(EPSON)應用于割草機慣性導航高性能陀螺儀傳感器SGPM01

93歲上將院士最新論文:三十年不斷發展的MEMS慣性傳感器(推薦)

軍工背景的慣性傳感器研發商「原極科技」獲數千萬元A輪融資





 MEMS慣性傳感器的慣性導航位姿解算基礎框架
MEMS慣性傳感器的慣性導航位姿解算基礎框架













評論