宏觀熱力學(xué)體系的相變臨界行為一直是統(tǒng)計(jì)力學(xué)研究的核心問題之一。臨界行為之所以重要和引人入勝是因?yàn)轶w系在臨界點(diǎn)處表現(xiàn)出較非臨界點(diǎn)處非常奇特的性質(zhì):內(nèi)部關(guān)聯(lián)長(zhǎng)度發(fā)散導(dǎo)致體系相較于其它非臨界點(diǎn)處出現(xiàn)巨大的熱漲落,進(jìn)而導(dǎo)致刻畫體系特征的各種響應(yīng)函數(shù)(對(duì)應(yīng)二階矩,與漲落有關(guān))在該點(diǎn)呈現(xiàn)出奇異性(發(fā)散或間斷點(diǎn)等非解析性)。本文將以氣液連續(xù)相變,平均場(chǎng)近似下Ising模型的連續(xù)相變,以及更為一般的Landau關(guān)于連續(xù)相變的唯象理論 — 二級(jí)相變理論為例,具體計(jì)算在每種情形下各種熱力學(xué)量和響應(yīng)函數(shù)的臨界行為,這個(gè)臨界行為由一組特征的臨界指數(shù)標(biāo)定。然后通過比較這些臨界指數(shù)我們可以發(fā)現(xiàn)這些看似完全不同的體系和處理手法在相變臨界點(diǎn)附近呈現(xiàn)出完全相同的物理行為,并由此揭示出相變臨界行為的普適性。最后探討這種普適性與體系內(nèi)部對(duì)稱性間的深刻聯(lián)系。
1氣液連續(xù)相變
在考慮了分子間的相互作用勢(shì)能后(即近端排斥遠(yuǎn)端吸引),我們可以對(duì)原始的無(wú)分子間相互作用的理想氣體狀態(tài)方程中的壓強(qiáng)和體積做修正。修正后最簡(jiǎn)單的物態(tài)方程即為范德瓦爾斯方程。現(xiàn)考慮1mol非理想氣體所滿足的如下的范德瓦爾斯方程。其中參數(shù),的值依賴于具體物質(zhì)(比如水分子有水分子的和,氫氣分子有氫氣分子的和)。我們將利用該方程來(lái)研究在臨界點(diǎn)處氣液連續(xù)相變的問題。
因?yàn)橄嘧兣R界點(diǎn)對(duì)應(yīng)于圖上的拐點(diǎn),所以此時(shí)壓強(qiáng)對(duì)體積的一階和二階偏導(dǎo)數(shù)均為0。容易解出臨界點(diǎn)處的體積,溫度和壓強(qiáng)分別是:
以臨界點(diǎn)的狀態(tài)值作為單位將原始的范德瓦爾斯方程改寫成與具體物質(zhì)無(wú)關(guān)的普適方程:
為直觀起見,【圖1】給出了上述普適方程在不同約化溫度下的函數(shù)圖像:
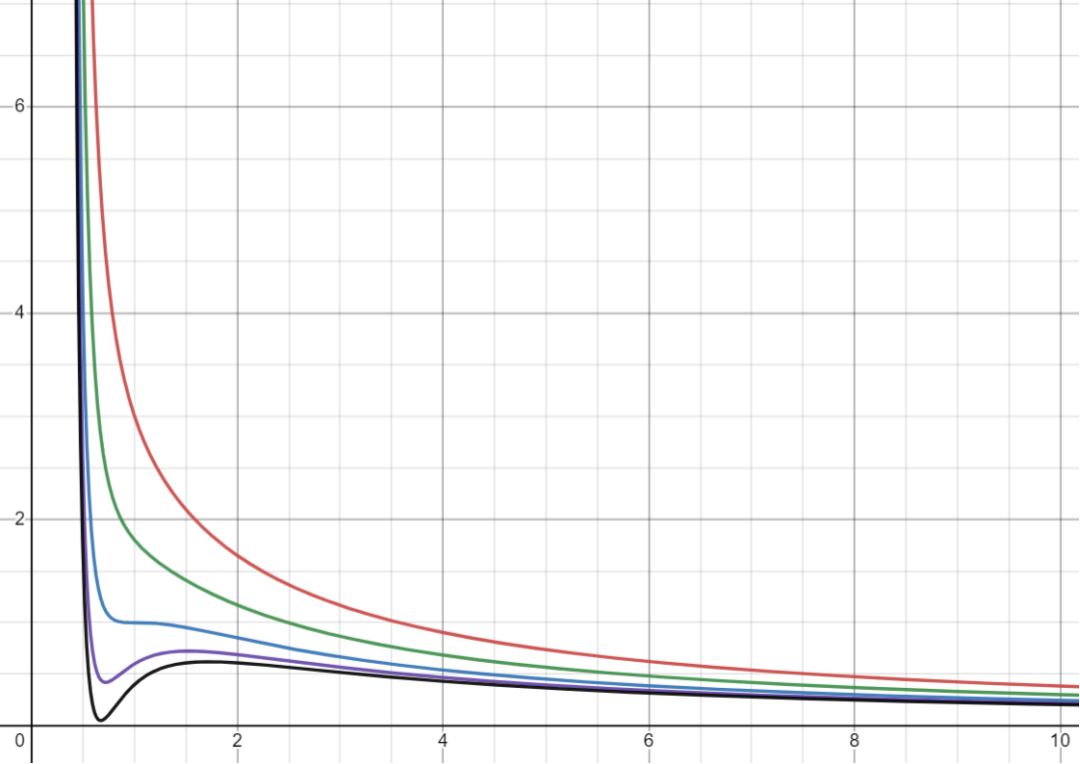
圖1 函數(shù)圖像。其中縱坐標(biāo)是約化壓強(qiáng),橫坐標(biāo)是約化體積。藍(lán)線代表約化溫度,對(duì)應(yīng)相變臨界點(diǎn)情形,藍(lán)線上面的綠線和紅線代表,下面的紫線和黑線代表
在臨界點(diǎn)附近對(duì)約化壓強(qiáng),體積,和溫度作小量展開到一階:
其中是臨界點(diǎn)附近的小量。所以普適方程可以寫成關(guān)于小量的形式:
為直觀起見,【圖2】給出了上式在不同下的函數(shù)圖像:
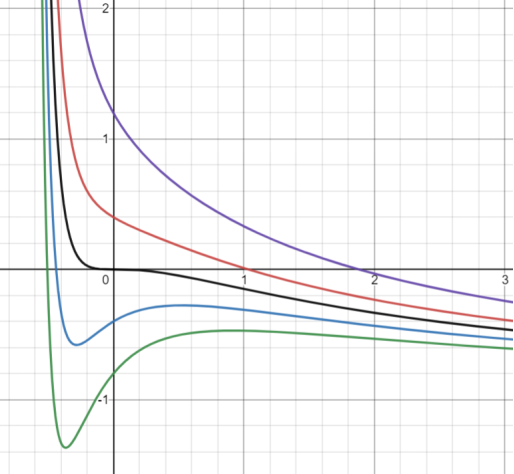
圖2 函數(shù)圖像。其中縱坐標(biāo)是約化壓強(qiáng)在臨界點(diǎn)附近展開對(duì)應(yīng)的小量,橫坐標(biāo)是約化體積在臨界點(diǎn)附近展開對(duì)應(yīng)的小量。黑線代表在臨界溫度時(shí)的關(guān)系,紅線和紫線代表臨界溫度以上的關(guān)系,藍(lán)線和綠線代表臨界溫度以下的關(guān)系
將上面關(guān)于小量的普適方程在附近泰勒展開:
從【圖2】可以看出,在臨界溫度以下時(shí),即時(shí),由于曲線的非單調(diào)性(即關(guān)于的多值性),所以體系必然存在氣液相變。在相變發(fā)生時(shí),根據(jù)兩相平衡條件,相和相(這里分別指代液相和氣相)的溫度,壓強(qiáng),和化學(xué)勢(shì)(吉布斯自由能)必須相同。根據(jù)兩相壓強(qiáng)相等的力學(xué)平衡條件可以得到:
根據(jù)等溫線上兩相化學(xué)勢(shì)相等的化學(xué)平衡條件可以得到:
將間的小量關(guān)系代入上式得到:
若假設(shè),則上述方程約化成:
所以意味著和同號(hào),與【圖2】()矛盾。所以先前的假設(shè)錯(cuò)誤。正確的關(guān)系只能是,也就是(關(guān)于縱軸對(duì)稱)。注意到這個(gè)關(guān)系對(duì)應(yīng)到【圖1】就是和關(guān)于臨界體積呈對(duì)稱分布。
接下來(lái)將化學(xué)平衡的結(jié)果代入到力學(xué)平衡的結(jié)果得到: , 。這個(gè)結(jié)果對(duì)應(yīng)于從臨界溫度下方趨于臨界點(diǎn)時(shí),氣相和液相間存在體積差, 也就是兩相間存在密度差(即兩相間不對(duì)稱,處于有序狀態(tài)!)。
但當(dāng)我們從臨界溫度上方趨于臨界點(diǎn)時(shí), 容易看出此時(shí)由于 曲線單調(diào), 為了同時(shí)滿足熱學(xué)平衡, 力學(xué)平衡和化學(xué)平衡條件, 只能取 , 對(duì)應(yīng)于此時(shí)的氣相和液相間不存在體積差, 也就是兩相間不存在密度差。所以嚴(yán)格來(lái)說(shuō),高于臨界溫度時(shí)其實(shí)只有一相(叫氣相也行,叫液相也行,因?yàn)閮上嚅g不存在密度差所以兩相完全對(duì)稱,處于無(wú)序狀態(tài)!無(wú)法區(qū)分誰(shuí)是氣體誰(shuí)是液體)。所以密度差是個(gè)關(guān)鍵的指標(biāo),它表征了體系當(dāng)前進(jìn)入到了哪種序。我們把這個(gè)關(guān)鍵的指標(biāo)叫做“序參量”!在我們現(xiàn)在考慮的氣液相變的例子里,兩相的密度差就可以充當(dāng)體系的序參量。
我們下面看它的臨界行為。當(dāng)從臨界溫度下方趨于臨界點(diǎn)時(shí):
當(dāng)從臨界溫度上方趨于臨界點(diǎn)時(shí):因?yàn)椋浴?/p>
所以如【圖3】所示,當(dāng)從臨界溫度下方趨于臨界點(diǎn)時(shí),序參量(密度差)是以的方式趨于0的;當(dāng)從臨界溫度上方趨于臨界點(diǎn)時(shí),序參量(密度差)恒為0。所以我們得出在氣液相變問題里序參量的臨界指數(shù)是1/2!因?yàn)榇藭r(shí)序參量(密度差,基本對(duì)應(yīng)吉布斯自由能的一階導(dǎo)數(shù))在臨界溫度處連續(xù),所以我們也稱這種相變叫“連續(xù)相變”。
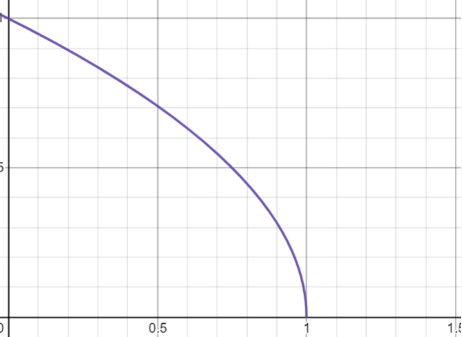
圖3 - 序參量(密度差)-溫度在臨界點(diǎn)附近的行為。縱坐標(biāo)是序參量(密度差),橫坐標(biāo)是溫度。序參量在臨界點(diǎn)左側(cè)非零標(biāo)志著體系進(jìn)入有序相,右側(cè)是零標(biāo)志著體系進(jìn)入無(wú)序相
下面看等溫壓縮率的臨界行為:
所以我們發(fā)現(xiàn)不管是從臨界溫度下方還是上方趨于臨界點(diǎn),等溫壓縮率都是以的方式趨于無(wú)窮大(發(fā)散)的(見【圖4】)!所以我們得出在氣液相變問題里等溫壓縮率的臨界指數(shù)是1!
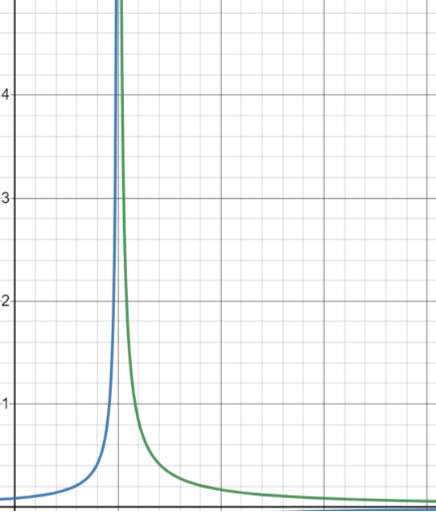
圖4 - 等溫壓縮率-溫度 在臨界溫度附近的發(fā)散行為。縱坐標(biāo)是等溫壓縮率,橫坐標(biāo)是溫度
因?yàn)榈葴貕嚎s率基本上是體積對(duì)壓強(qiáng)的一階導(dǎo)數(shù),而體積又基本上是吉布斯自由能對(duì)壓強(qiáng)的一階導(dǎo)數(shù),所以等溫壓縮率基本上是吉布斯自由能對(duì)壓強(qiáng)的二階導(dǎo)數(shù)。也就是說(shuō)在臨界溫度處,吉布斯自由能對(duì)壓強(qiáng)的二階導(dǎo)數(shù)出現(xiàn)奇異性(發(fā)散)!吉布斯自由能對(duì)熱力學(xué)參數(shù)的二階導(dǎo)數(shù)一般對(duì)應(yīng)到體系的響應(yīng)函數(shù)。所以此時(shí)響應(yīng)函數(shù)在臨界點(diǎn)附近出現(xiàn)奇異性。這種連續(xù)相變一般被稱作“二級(jí)相變”。
下面看等容比熱的臨界行為(由于此時(shí)氣液相變系統(tǒng)的所有信息是以關(guān)于, , 的物態(tài)方程而不是以自由能或配分函數(shù)的形式給出的,所以這里等容比熱的計(jì)算相當(dāng)繁瑣,這里直接給出結(jié)論):
所以我們發(fā)現(xiàn)不管是從臨界溫度下方還是上方趨于臨界點(diǎn),等容比熱都是以的方式發(fā)生奇異性(間斷點(diǎn))的!所以我們得出在氣液相變問題里等容比熱的臨界指數(shù)是0!
根據(jù)先前關(guān)于小量的物態(tài)方程易知:當(dāng)固定在等溫線(即)時(shí),偏離壓強(qiáng)和體積臨界值的小量間滿足三次方的關(guān)系:(見【圖5】)。或者用原始的量可以把關(guān)系表示成: 。這里的臨界指數(shù)3也是標(biāo)定氣液相變臨界行為的一個(gè)特征指標(biāo)!
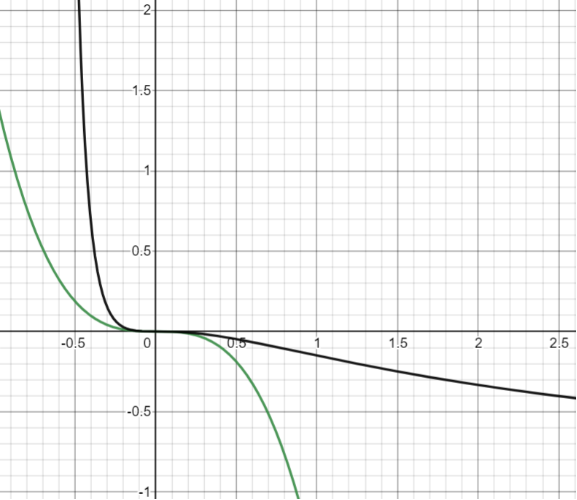
圖5 - 縱坐標(biāo)是壓強(qiáng)偏離的小量,橫坐標(biāo)是體積偏離的小量。綠線代表壓強(qiáng)相對(duì)體積的三次方的臨界行為,黑線代表原始未作近似的嚴(yán)格的臨界溫度上壓強(qiáng)-體積的行為。可以發(fā)現(xiàn)在坐標(biāo)原點(diǎn)附近,黑線基本與綠線重合
2平均場(chǎng)近似下Ising模型的連續(xù)相變
考慮一個(gè)任意維度下的Ising模型。在平均場(chǎng)近似下,我們把Ising形式的相互作用等效成了外磁場(chǎng)的一部分,使得體系被近似成一個(gè)等效的“無(wú)相互作用”體系。在統(tǒng)計(jì)力學(xué)的框架下通過對(duì)Ising形式正則配分函數(shù)的操作,容易得到關(guān)于平均磁化的自洽方程。當(dāng)外場(chǎng)時(shí)(也就是考慮自發(fā)磁化),臨界點(diǎn)附近的平均磁化是個(gè)小量。所以將自洽方程關(guān)于小量展開得到:
其中特征溫度。上述自洽方程其中一個(gè)解是,其余兩個(gè)解是否存在取決于以下方程右側(cè)是否大于0:
當(dāng)時(shí),方程右側(cè)小于0,故原方程只有這個(gè)解;
當(dāng)時(shí),方程右側(cè)大于0,故原方程除了有的解,還有
這兩個(gè)解。由于對(duì)應(yīng)的Helmholtz自由能比時(shí)的自由能來(lái)得高,所以是非穩(wěn)定態(tài)必須舍去。所以當(dāng)體系從臨界溫度下方逼近臨界點(diǎn)時(shí),的臨界行為是:
當(dāng)體系從臨界溫度上方逼近臨界點(diǎn)時(shí),。
所以如【圖6】所示,當(dāng)從臨界溫度下方趨于臨界點(diǎn)時(shí),序參量(平均自發(fā)磁化)是以的方式趨于0的;當(dāng)從臨界溫度上方趨于臨界點(diǎn)時(shí),序參量(平均自發(fā)磁化)恒為。所以我們得出在平均場(chǎng)近似下Ising模型里序參量的臨界指數(shù)是!這個(gè)結(jié)果和之前氣液相變里序參量(密度差)的臨界指數(shù)完全一樣!
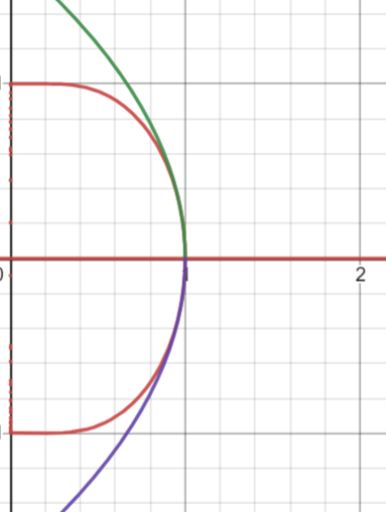
圖6 - 在外場(chǎng)時(shí),縱軸代表平均磁化,橫軸代表溫度。紅線是嚴(yán)格按照平均場(chǎng)近似下的自洽方程給出的平均磁化-溫度的函數(shù)關(guān)系,綠線和紫線是按照臨界點(diǎn)附近對(duì)自洽方程作小量展開近似后出來(lái)的結(jié)果。可以發(fā)現(xiàn)在臨界點(diǎn)附近,它們與紅線基本完全重合
下面看等溫磁化率的臨界行為。由于此時(shí)需要考慮磁場(chǎng)的變動(dòng),所以我們需要使用原始帶的自洽方程:
所以體系的磁化率是:
根據(jù)之前的結(jié)論,當(dāng)外場(chǎng)趨于0且從臨界溫度下方趨于臨界點(diǎn)時(shí), ,所以:
當(dāng)從臨界溫度上方趨于臨界點(diǎn)時(shí),, ,所以:
所以我們發(fā)現(xiàn)不管是從臨界溫度下方還是上方趨于臨界點(diǎn),等溫磁化率都是以的方式(類似宏觀順磁性的居里定律)趨于無(wú)窮大(發(fā)散)的(見【圖7】)!所以我們得出在平均場(chǎng)近似下Ising模型里等溫磁化率的臨界指數(shù)是1!這個(gè)結(jié)果和之前氣液相變里等溫壓縮率的臨界指數(shù)完全一樣!
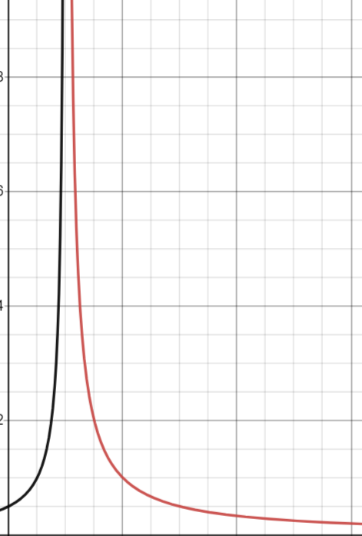
圖7 - 等溫磁化率-溫度在臨界溫度附近的發(fā)散行為。縱坐標(biāo)是等溫磁化率,橫坐標(biāo)是溫度
下面考慮無(wú)外磁場(chǎng)時(shí)比熱的臨界行為。思路是從Ising體系的正則配分函數(shù)出發(fā)求得內(nèi)能,然后通過內(nèi)能在臨界點(diǎn)附近的行為推斷出比熱的臨界行為:
當(dāng)從臨界溫度下方趨于臨界點(diǎn)時(shí),, ,所以:
所以當(dāng)從臨界溫度下方趨于臨界點(diǎn)時(shí)比熱是:
當(dāng)從臨界溫度上方趨于臨界點(diǎn)時(shí),,,所以容易看出比熱是:
所以我們發(fā)現(xiàn)不管是從臨界溫度下方還是上方趨于臨界點(diǎn),比熱都是以的方式發(fā)生奇異性(間斷點(diǎn))的!所以我們得出在平均場(chǎng)近似下Ising模型里比熱的臨界指數(shù)是0!這個(gè)結(jié)果和之前氣液相變里等容比熱的臨界指數(shù)完全一樣!
最后看固定在臨界溫度上,當(dāng)外磁場(chǎng)很弱的情況下,和(或)的關(guān)系:
因?yàn)樵谂R界點(diǎn)附近且很小,所以也很小。所以里宗量很小。所以方程右端可以展開成
所以如【圖8】所示,當(dāng)固定在臨界溫度時(shí)(且外場(chǎng)很小時(shí)),磁場(chǎng)和平均磁化或平均磁矩間滿足三次方的關(guān)系:或。這里的臨界指數(shù)3也是標(biāo)定平均場(chǎng)近似下Ising模型臨界行為的一個(gè)特征指標(biāo)!這個(gè)結(jié)果和之前氣液相變里偏離壓強(qiáng)和體積臨界值的小量間滿足的關(guān)系所對(duì)應(yīng)的臨界指數(shù)3,即,完全一樣!
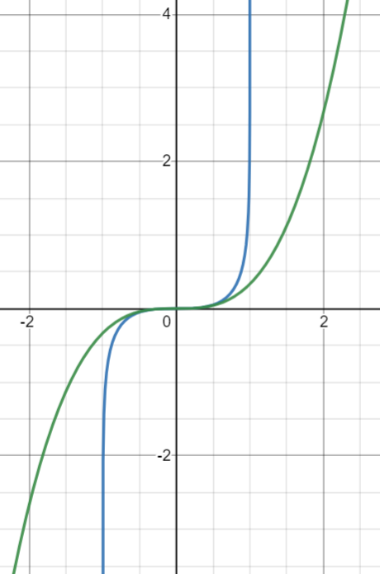
圖8 - 縱坐標(biāo)是磁場(chǎng),橫坐標(biāo)是平均磁化。綠線代表磁場(chǎng)相對(duì)平均磁化的三次方的臨界行為,藍(lán)線代表原始未作近似的嚴(yán)格的臨界溫度上磁場(chǎng)-平均磁化的行為。可以發(fā)現(xiàn)在坐標(biāo)原點(diǎn)附近,藍(lán)線基本與綠線重合
3連續(xù)相變的唯象理論 — Landau二級(jí)相變理論
從(1)和(2)的分析中可以發(fā)現(xiàn)體系在臨界點(diǎn)處發(fā)生相變的過程其實(shí)是一種從高溫時(shí)的無(wú)序態(tài)到低溫時(shí)的有序態(tài)的變化過程。其中氣液相變例子里的序就是液體和氣體的密度差(或體積差),平均場(chǎng)近似下Ising模型例子里的序就是平均磁化。這種序的變化本質(zhì)上體現(xiàn)出的是體系對(duì)稱性的破缺,是刻畫相變特征的極重要的內(nèi)稟參數(shù),被叫做“序參量”。所以我們可以唯象地把序參量寫進(jìn)一個(gè)叫做Landau自由能的表達(dá)式中。假定這個(gè)Landau自由能在臨界點(diǎn)附近解析,則它可以被展開成關(guān)于序參量的多項(xiàng)式函數(shù)。然后體系真實(shí)的自由能對(duì)應(yīng)于Landau自由能的極小值/穩(wěn)定態(tài)。【注意這個(gè)內(nèi)稟序參量的變化不能人為直接控制,只能通過間接調(diào)控外界壓強(qiáng)和溫度等間接控制。】
值得注意的是:因?yàn)槲覀兗俣w系具有反演不變性,所以這里的Landau自由能函數(shù)里沒有關(guān)于序參量的三次方項(xiàng)。
首先考慮自發(fā)磁化,即當(dāng)外場(chǎng)時(shí)Landau自由能函數(shù)的行為:
所以可以解出三個(gè)極值點(diǎn),其中1個(gè)零解加上另外一對(duì)互為相反數(shù)的非零解(注意:取決于和的具體符號(hào),因?yàn)樵诟?hào)里面,這一對(duì)解在有些時(shí)候不一定存在):
我們希望找到穩(wěn)定的極值點(diǎn),也就是最小的地方作為系統(tǒng)可以穩(wěn)定存在的狀態(tài)。所以基于這個(gè)要求,首先必須讓四次項(xiàng)前面的系數(shù)以保證當(dāng)時(shí)不會(huì)變成負(fù)無(wú)窮大(那樣的話系統(tǒng)的穩(wěn)定態(tài)就要落在的地方以保證能量最低,這顯然是不合理的)。由于,所以二次項(xiàng)前面的系數(shù)的正負(fù)直接決定了是否存在非零解。
當(dāng)時(shí),非零解根號(hào)里的宗量小于0,此時(shí)只存在的唯一解。為了知道的解對(duì)應(yīng)的極小值(穩(wěn)定態(tài))還是極大值(非穩(wěn)定態(tài)),我們看對(duì)序參量的二階導(dǎo)數(shù)在處的符號(hào),如果是正號(hào)就意味著這對(duì)應(yīng)穩(wěn)定態(tài),否則就是非穩(wěn)定態(tài):
所以處對(duì)應(yīng)能量的極小值,確實(shí)對(duì)應(yīng)時(shí)的穩(wěn)定態(tài)。為直觀起見,作出此時(shí)的函數(shù)關(guān)系草圖(【圖9】類似一個(gè)“”型曲線):
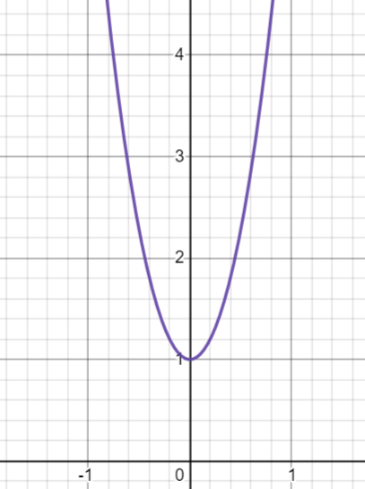
圖9 - ,,縱坐標(biāo)是自由能,橫坐標(biāo)是序參量。容易看出處對(duì)應(yīng)該函數(shù)的極小值(穩(wěn)定態(tài)),所以此時(shí)系統(tǒng)處于高溫下的無(wú)序相(完全對(duì)稱!)
從另一方面看,又代表高于相變臨界溫度時(shí)的無(wú)序相。所以我們以序參量 為橋梁找到一個(gè)對(duì)應(yīng)關(guān)系,即:時(shí)。
當(dāng)時(shí),非零解根號(hào)里的宗量大于0,此時(shí)存在3個(gè)極值點(diǎn),即最開始列出的:
為了知道這3個(gè)解對(duì)應(yīng)的極小值(穩(wěn)定態(tài))還是極大值(非穩(wěn)定態(tài)),我們看對(duì)序參量的二階導(dǎo)數(shù)在這3處的符號(hào),如果是正號(hào)就意味著對(duì)應(yīng)穩(wěn)定態(tài),否則就是非穩(wěn)定態(tài):
所以處對(duì)應(yīng)能量的極大值,是非穩(wěn)定態(tài)。而處對(duì)應(yīng)能量極小值,是穩(wěn)定態(tài)。所以體系此時(shí)處于的穩(wěn)定態(tài)。為直觀起見,作出此時(shí)的函數(shù)關(guān)系草圖(【圖10】類似一個(gè)“”型曲線):
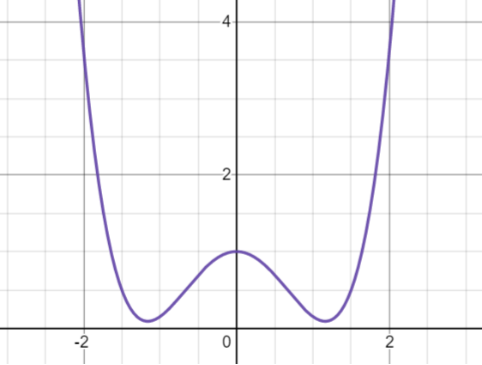
圖10 - ,,縱坐標(biāo)是自由能,橫坐標(biāo)是序參量。容易看出處對(duì)應(yīng)該函數(shù)的極大值(非穩(wěn)定態(tài)),處對(duì)應(yīng)該函數(shù)的極小值(穩(wěn)定態(tài))。所以此時(shí)系統(tǒng)處于低溫下的有序相(對(duì)稱性破缺!)
從另一方面看,又代表低于相變臨界溫度時(shí)的有序相。所以我們以序參量為橋梁又找到一個(gè)對(duì)應(yīng)關(guān)系,即:時(shí) 。
所以綜上所述,我們找到了Landau自由能函數(shù)二次項(xiàng)前面的系數(shù)A和溫度T在臨界溫度附近的關(guān)系,即:時(shí);而時(shí)。
出于連續(xù)性的考慮可以推斷出恰好在臨界溫度時(shí)。為直觀起見,作出此時(shí)的函數(shù)關(guān)系草圖(【圖11】類似一個(gè)“”型曲線):

圖11 -,,縱坐標(biāo)是自由能,橫坐標(biāo)是序參量。容易看出處對(duì)應(yīng)該函數(shù)的極小值(穩(wěn)定態(tài)),但相較于圖9,此處在極小值點(diǎn)附近有一個(gè)接近于平坦的谷底,對(duì)應(yīng)于相變臨界點(diǎn)處關(guān)聯(lián)長(zhǎng)度趨于無(wú)窮大。溫度稍微提升一點(diǎn)圖11就會(huì)進(jìn)入圖9的無(wú)序相,溫度稍微下降一點(diǎn)就會(huì)進(jìn)入圖10的有序相
根據(jù)上述和溫度的關(guān)系,可以把在處作泰勒展開到一階:
其中。當(dāng)從臨界溫度下方趨于臨界點(diǎn)時(shí),由于還在有序相,所以:
當(dāng)從臨界溫度上方趨于臨界點(diǎn)時(shí),由于在無(wú)序相,所以。所以當(dāng)從臨界溫度下方趨于臨界點(diǎn)時(shí),序參量是以的方式趨于0的;當(dāng)從臨界溫度上方趨于臨界點(diǎn)時(shí),序參量恒為0。所以我們得出Landau二級(jí)相變理論里序參量的臨界指數(shù)是1/2!這個(gè)結(jié)果和之前氣液相變里序參量(密度差)的臨界指數(shù)以及平均場(chǎng)近似下Ising模型里序參量(平均自發(fā)磁化)的臨界指數(shù)完全一樣!
下面看Landau二級(jí)相變理論里磁化率的臨界行為。磁化率的計(jì)算牽涉到磁場(chǎng)的變化。所以我們必須使用帶有磁場(chǎng)的Landau自由能展開。這個(gè)附加的磁場(chǎng)是通過與序參量(這里的可以解釋成磁矩)一次方形式的耦合進(jìn)入到Landau自由能的,即:
【注意如果我們處理的不是磁性體系和磁化率,而是希望用Landau自由能描述氣液相變里壓縮系數(shù)的臨界行為的話,只需要把這里的序參量解釋成密度差(或體積差),外場(chǎng)解釋成壓強(qiáng)即可。】
在系統(tǒng)穩(wěn)定態(tài)處Landau自由能取極值:
所以體系磁化率是:
當(dāng)從臨界溫度下方趨于臨界點(diǎn)時(shí),由于還在有序相,且磁場(chǎng)為0,所以,代入到上面關(guān)于的表達(dá)式得到:
當(dāng)從臨界溫度上方趨于臨界點(diǎn)時(shí),由于在無(wú)序相,且磁場(chǎng)為0,所以,代入到上面關(guān)于的表達(dá)式得到:
所以我們發(fā)現(xiàn)不管是從臨界溫度下方還是上方趨于臨界點(diǎn),磁化率都是以的方式趨于無(wú)窮大(發(fā)散)的!所以我們得出Landau二級(jí)相變理論里磁化率的臨界指數(shù)是1!這個(gè)結(jié)果和之前氣液相變里等溫壓縮率的臨界指數(shù)以及平均場(chǎng)近似下Ising模型里等溫磁化率的臨界指數(shù)完全一樣!
下面再看Landau二級(jí)相變理論里比熱的臨界行為。在比熱的討論里和外磁場(chǎng)沒關(guān)系,所以。所以Landau自由能的形式退化成:
體系的化學(xué)勢(shì)(吉布斯自由能)取在Landau自由能的極小值(穩(wěn)定態(tài))處。所以在臨界溫度以下()時(shí),體系的化學(xué)勢(shì)取在Landau自由能的地方,即:
在臨界溫度以上()時(shí),體系的化學(xué)勢(shì)取在Landau自由能的地方,即:
所以臨界溫度以下()時(shí)體系的熵是:
臨界溫度以上()時(shí)體系的熵是:
所以可以進(jìn)一步求出從臨界溫度下方趨于臨界點(diǎn)時(shí)體系的比熱是:
從臨界溫度上方趨于臨界點(diǎn)時(shí)體系的比熱是:
所以我們發(fā)現(xiàn)不管是從臨界溫度下方還是上方趨于臨界點(diǎn),比熱都是以的方式發(fā)生奇異性(間斷點(diǎn))的!所以我們得出Landau二級(jí)相變理論里比熱的臨界指數(shù)是0!這個(gè)結(jié)果和之前氣液相變里等容比熱的臨界指數(shù)以及平均場(chǎng)近似下Ising模型里比熱的臨界指數(shù)完全一樣!
最后看固定在臨界溫度上,當(dāng)外磁場(chǎng)很弱的情況下,和的關(guān)系。此時(shí)二次項(xiàng)前面的系數(shù),并且因?yàn)榻酉聛?lái)的計(jì)算牽涉到磁場(chǎng)的變化,所以我們必須使用帶有磁場(chǎng)的Landau自由能展開。這個(gè)附加的磁場(chǎng)是通過與序參量 (這里的可以解釋成磁矩)一次方形式的耦合進(jìn)入到Landau自由能的。所以Landau自由能的形式是:
在系統(tǒng)穩(wěn)定態(tài)處Landau自由能取極值:
所以固定在臨界溫度時(shí)(且外場(chǎng)很小時(shí)),磁場(chǎng)和序參量間滿足三次方的關(guān)系:。這里的臨界指數(shù)3也是標(biāo)定Landau二級(jí)相變理論的一個(gè)特征指標(biāo)!這個(gè)結(jié)果和之前氣液相變里偏離壓強(qiáng)和體積臨界值的小量間滿足的關(guān)系所對(duì)應(yīng)的臨界指數(shù)3,即,以及平均場(chǎng)近似下Ising模型里的磁場(chǎng)和平均磁化或平均磁矩間滿足的關(guān)系所對(duì)應(yīng)的臨界指數(shù)3,即或,完全一樣!
4對(duì)稱性和普適類
所以從上面的分析中我們發(fā)現(xiàn)在臨界點(diǎn)附近:氣液相變,平均場(chǎng)近似下的Ising模型,和更為抽象一般的Landau二級(jí)相變理論都給出了完全相同的一組臨界指數(shù)!看起來(lái)相互間沒有任何關(guān)系的體系(氣液相變,Ising鐵磁相變體系,和Landau二級(jí)相變理論所描述的更為抽象一般的體系),出發(fā)點(diǎn)和處理手法也完全不同(氣液相變里是從非理想氣體所滿足的物態(tài)方程出發(fā),Ising鐵磁相變體系是從平均磁化滿足的自洽方程出發(fā),Landau二級(jí)相變理論是從作為序參量的多項(xiàng)式函數(shù)的Landau自由能出發(fā)),竟然在臨界點(diǎn)附近的行為表現(xiàn)出驚人的一致性!!!
這種一致性產(chǎn)生的根本原因在于:氣液連續(xù)相變,Ising鐵磁相變體系,和Landau二級(jí)相變所描述的更為抽象的體系具有完全相同的對(duì)稱性,即所謂的對(duì)稱性!所以它們所描述的體系處于完全相同的普適類里!如果把普適類看成是一類幾何/拓?fù)鋵?duì)象,那么這些臨界指數(shù)就可以看成是標(biāo)定這個(gè)幾何/拓?fù)鋵?duì)象特征的“拓?fù)洳蛔兞俊保∵@些“拓?fù)洳蛔兞俊焙途唧w物質(zhì)(可以類比成對(duì)象局域的幾何性質(zhì))無(wú)關(guān),而只與體系的對(duì)稱性(可以類比成對(duì)象本身的拓?fù)湫再|(zhì),比如虧格和纏繞數(shù))有關(guān),具有普適性。
然而值得注意的是,這個(gè)普適性也是有限度的。比如這三套理論對(duì)于比熱臨界指數(shù)的估計(jì)都是0(這與實(shí)驗(yàn)中測(cè)出的非零的比熱臨界指數(shù)差別很大),這是因?yàn)樗鼈兺耆雎缘袅梭w系本身的熱漲落效應(yīng),所以它們只能給出一種特殊的普適類。對(duì)于具有別的對(duì)稱性的體系(比如二維XY模型),它將屬于別的普適類。別的普適類將由別的一組臨界指數(shù)標(biāo)定。
所以自然界中千差萬(wàn)別的體系可以被劃分進(jìn)不同的普適類里,每個(gè)普適類內(nèi)部的所有系統(tǒng)在臨界點(diǎn)附近都是完全等價(jià)的,所以只要研究清楚普適類里其中一個(gè)系統(tǒng)在臨界點(diǎn)處的行為,我們就可以直接推斷出別的和它在同一個(gè)普適類里的其它系統(tǒng)在臨界點(diǎn)處的行為!所以對(duì)不同的具體系統(tǒng)的物理性質(zhì)的研究可以轉(zhuǎn)化為對(duì)不同普適類的抽象數(shù)學(xué)性質(zhì)的研究!而這也是相變和臨界現(xiàn)象問題里最引人入勝的地方之一。
是呢環(huán)保局:郭婷
-
函數(shù)
+關(guān)注
關(guān)注
3文章
4338瀏覽量
62739
原文標(biāo)題:統(tǒng)計(jì)力學(xué) – 連續(xù)相變的臨界行為和普適性
文章出處:【微信號(hào):bdtdsj,微信公眾號(hào):中科院半導(dǎo)體所】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
探討篇(三):代碼復(fù)用的智慧 - 提升架構(gòu)的效率與可維護(hù)性

對(duì)稱加密技術(shù)在實(shí)際應(yīng)用中如何保障數(shù)據(jù)安全?
中海達(dá)普適型監(jiān)測(cè)設(shè)備的應(yīng)用案例
華納云:Chord算法如何管理節(jié)點(diǎn)間的聯(lián)系?
智能系統(tǒng)的安全性分析

運(yùn)放的哪些參數(shù)可以反映出它的不對(duì)稱性?
維愛普 EMC濾波器:電子設(shè)備的電磁兼容性守護(hù)者
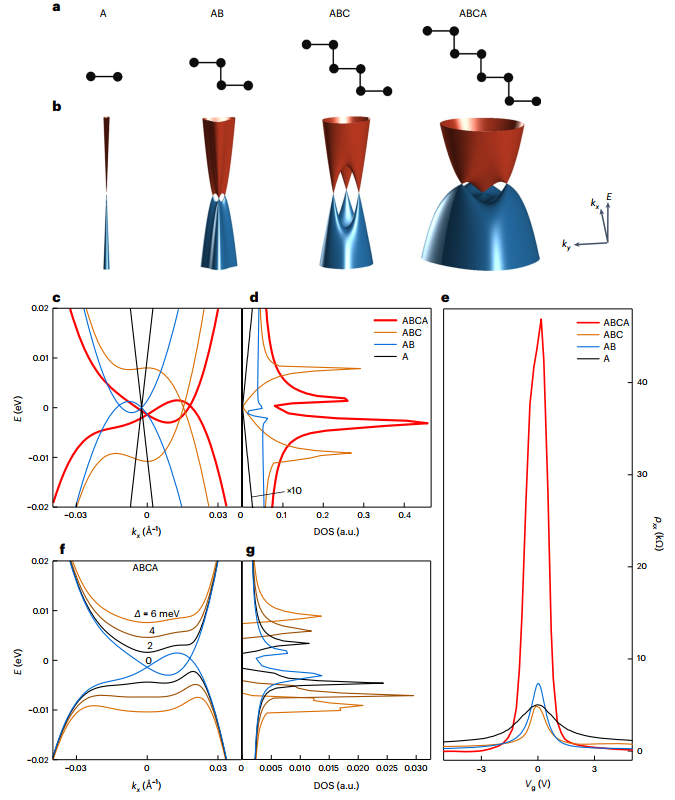
鎖相放大器在觀察石墨烯自發(fā)對(duì)稱性破缺的量子輸運(yùn)測(cè)量
什么是電源濾波器 常用電源濾波器電路形式
對(duì)稱電池測(cè)試怎么分析?什么是軟短路,什么是硬短路?
基于架構(gòu)設(shè)計(jì)的車載網(wǎng)聯(lián)系統(tǒng)驗(yàn)證體系研究





 普適性與體系內(nèi)部對(duì)稱性間的深刻聯(lián)系探討
普適性與體系內(nèi)部對(duì)稱性間的深刻聯(lián)系探討










評(píng)論