作為一個材料人,必須要掌握材料的基本力學性質,包括應變、應力以及相互之間的關系等。需要了解材料在不同形式的力的作用下的對應的反應形式,并儲備常用的材料的力學性質的知識。選擇合理的數學模型,確定最終的物理方程,這都要求我們了解材料的基本力學性質。
材料的力學性質通常是由試驗測定的。因此,力學性質分為單項加載情況下的力學特征、單項加載卸載的力學特征、循環加載時材料力學特征。其中,單項加載情況下獲得的基本力學數據是比較基礎的。進行相關的描述前,首先需要了解力學的基本概念,包括應變、應力。
所觀察的物體的變化從物理上來講主要包含位置的變化和形狀的變化。位置變化可以通過旋轉、平移來表達,形狀的變化則是可以通過應變來表達。應變包括長度的變化和方向的變化。如下圖所示,長度的相對變化為線應變,可以表示為:
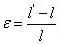
方向的相對改變為剪(角)應變,如:
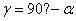
針對三維情形,可以獲得應變張量如式:
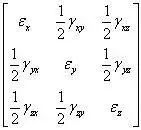
需要說明的是,張量的剪切應變分量不等于實際的剪切應變。
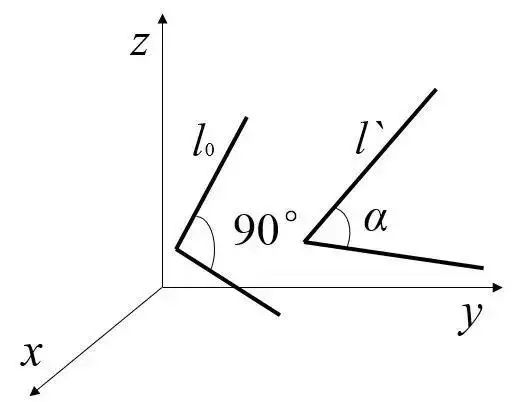
圖1 應變表達示意圖
上述定義屬于工程應變。工程應變取決于初始長度,如l,初始長度是事先已知的,所以工程應變是線性的。工程應變的應用局限于材料小旋轉,中等大小的剛體旋轉將導致非零應變。實際上,一切能夠按照一定的規律表示形狀變化的量均可以作為應變的度量(但應變的使用通常需要和應力產生極大的關聯,方能產生實際價值,因此,需要針對所定義的應變度量建立相關聯的應力度量,即共軛的應力定義)。所以,除了上述應變定義以外,還有其他一些比較重要的應變定義。一維問題中,對數應變由下面公式計算:
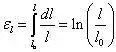
對數應變也可以泰勒展開如下式所示,其與工程應變存在一定的差別,因此,需要進行區別對待。在有限元程序編寫時,特別是靜強度分析時,通常為小應變狀態,且所劃分的單元較小,因此,兩者的差別并不大。
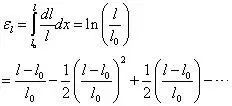
對數應變是非線性應變,因為它是未知的最終長度的非線性函數。它同樣可稱為log應變。三維等效對數應變是Hencky應變。在大應變問題中,對數應變并不能自動適應任意大的旋轉。
一維的Green-Lagrange應變由下式計算:
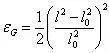
此應變是非線性的,因為它取決于未知的更新長度的平方。此種應變優于對數應變或Hencky應變之處在于,它可自動適應大應變問題中的任意大旋轉。這在非線性分析中將會用到。常見的力學試驗拉伸數據如下圖所示。
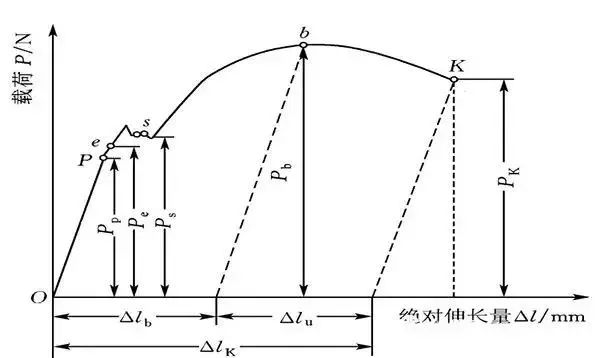
僅從幾何學的角度定義如上,直觀易于理解,但實際應用過程中,這種純粹幾何的定義適應性較差,通常需要從解析幾何的角度來進一步地考慮。因此,需要首先建立坐標系。
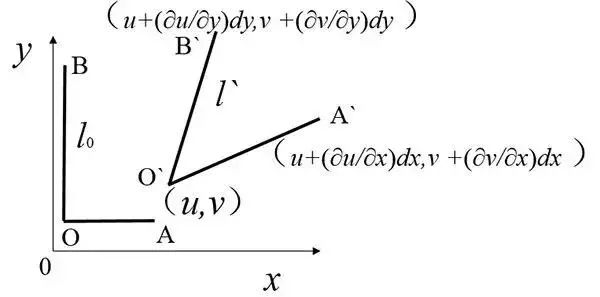
圖2 位移示意圖
OA和OB兩線元的長度分別為OA=dx,OB=dy。設O點的位移是u(x, y) 和v(x, y),A 點的位移是u(x+dx, y)、v(x+dx,y),
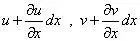
B點的位移是u(x,y+dy)、v(x,y+dy)。
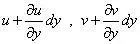
則可以定義工程應變如下式所示。
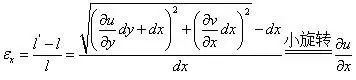
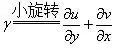
可以看出,上述的位移的描述都是基于最初狀態下的位形確定的,我們可以稱為0時刻狀態下的位形。顯然位形發生變化可以通過上述的量進行表達。
那么,對數應變、Green-Lagrange應變應當如何表達呢?
如果我們觀察物體上一個點的運動,它的初始位置是{X},最終位置是{x},它運動的量為{u}。
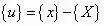
變形梯度也是物體變形多少的一個度量,它的定義是:
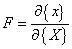
變形梯度F,可以過濾掉平動(在通過后續對數計算等可以將平動給過濾掉,實際上F在平動時應該為單位矩陣),剩余旋轉、由于應變造成的形狀改變。通過矩陣的極分解,可以獲得去除了旋轉變換后的形狀變形。
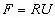
對數 (Hencky) 應變可由下式計算:
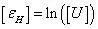
這里對數應變是以矩陣形式表示的應變張量。在三維問題中,Green-Lagrange 應變可直接由拉伸矩陣計算出,如下式所示:
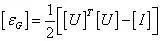
這種應變在計算時直接忽略了旋轉矩陣,則可以從變形梯度的形式寫出,如下式所示,前兩項是線性小應變項,最后一項是應變的非線性項。
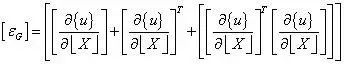
當然以上的形式可以通過變形前的坐標進行表示,也可以通過變形后的坐標進行表示。更新拉格朗日應變即為ALMANSI應變。此外,常用的概念還有體積應變。
審核編輯 :李倩
-
材料
+關注
關注
3文章
1220瀏覽量
27270 -
力學
+關注
關注
0文章
50瀏覽量
15197
原文標題:【知識】材料力學性質的基礎認識——應變
文章出處:【微信號:深圳市賽姆烯金科技有限公司,微信公眾號:深圳市賽姆烯金科技有限公司】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
超導材料的性質與特征 比較不同超導材料的優缺點
導磁材料的主要性質有哪些
材料試驗機:工業品質的守護者





 材料力學性質的基礎認識——應變
材料力學性質的基礎認識——應變











評論