函數式編程是一種歷史悠久的編程范式。作為演算法，它的歷史可以追溯到現代計算機誕生之前的λ演算，本文希望帶大家快速了解函數式編程的歷史、基礎技術、重要特性和實踐法則。

在內容層面，主要使用JavaScript語言來描述函數式編程的特性，并以演算規則、語言特性、范式特性、副作用處理等方面作為切入點，通過大量演示示例來講解這種編程范式。同時，文末列舉比較一些此范式的優缺點，供讀者參考。

1. 前文回顧

2. 本文簡介

3. 副作用處理：單子Monad，一種不可避免的抽象

3.1 什么是Monad？

3.2 范疇、群、幺半群

3.3 Monad范疇：定律、折疊和鏈

3.4 Maybe和Either

3.5 IO的處理方式

4. 函數式編程的應用

4.1 設計一個請求模塊

4.2 設計一個輸入框

4.3 超長文本省略：Ramdajs為例

5. 函數式編程庫、語言

6. 總結

6.1 優點

6.2 不足

7. FAQ

1. 前文回顧

在上篇中，我們分析了函數式編程的起源和基本特性，并通過每一個特性的示例來演示這種特性的實際效果。首先，函數式編程起源于數理邏輯，起源于λ演算，這是一種演算法，它定義一些基礎的數據結構，然后通過歸約和代換來實現更復雜的數據結構，而函數本身也是它的一種數據。其次，我們探討了很多函數式編程的特性，比如：

First Class

純函數

引用透明

表達式

高階函數

柯里化

函數組合

point-free

...

但我們也指出了一個實際問題：不能處理副作用的程序是毫無意義的。我們的計算機程序隨時都在產生副作用。我們程序里面有大量的網絡請求、多媒體輸入輸出、內部狀態、全局狀態等，甚至在提倡“碳中和”的今天，電腦的發熱量也是一個不容小覷的副作用。那么我們應該如何處理這些問題呢？

2. 本文簡介

本文通過深入函數式編程的副作用處理及實際應用場景，提供一個學習和使用函數式編程的視角給讀者。一方面，這種副作用管理方式是一種高級的抽象形式，不易理解；另一方面，我們在學習和使用函數式編程的過程中，幾乎都會遇到類似的副作用問題需要解決，能否解決這個問題也決定了一門函數式編程語言最終是否能走上成功。

本文主要分為三個部分：

副作用處理方式

函數式編程的應用

函數式編程的優缺點比較

3. 副作用處理：單子Monad，一種不可避免的抽象

上面說的，都是最基礎的JavaScript概念+函數式編程概念。但我們還留了一個“坑”。

如何去處理IO操作？

我們的代碼經常在和副作用打交道，如果要滿足純函數的要求，幾乎連一個需求都完成不了。不用急，我們來看一下React Hooks。React Hooks的設計是很巧妙的，以useEffect為例：

圖 43

在函數組件中，useState用來產生狀態，在使用useEffect的時候，我們需要掛載這個state到第二個參數，而第一個參數給到的運行函數在state變更的時候被調用，被調用時得到最新的state。

這里面有一個狀態轉換：

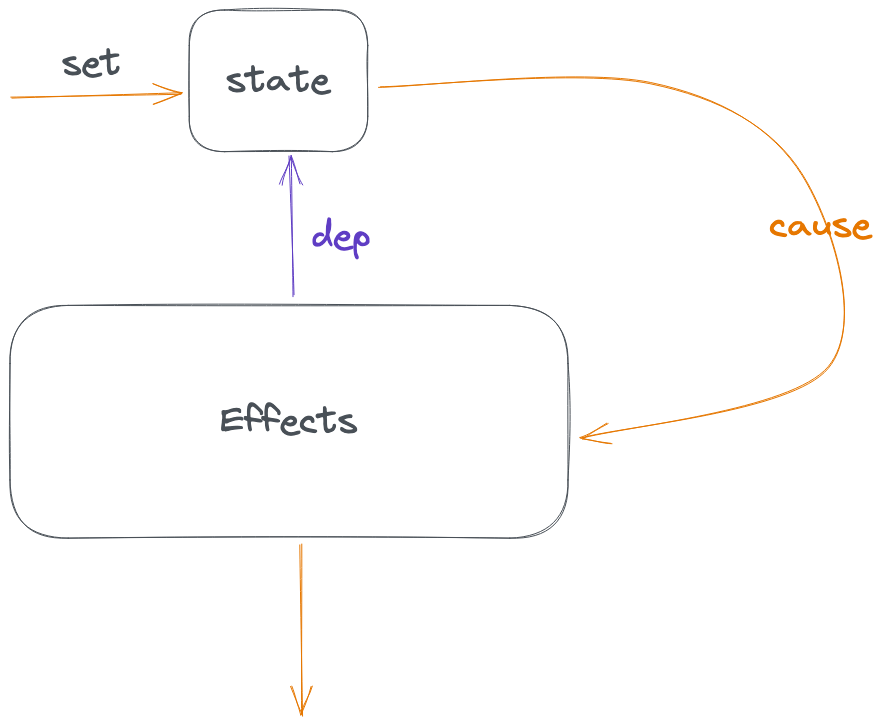
圖 44

React Hooks給我們的啟發是，副作用都被放到一個狀態節點里面去被動觸發，形成一個單向的數據流動。而實際上，函數式編程語言確實也是這么做的，把副作用包裹到一個特殊的函數里面。

如果一個函數既包含了我們的值，又封裝了值的統一操作，使得我們可以在它限定的范圍內進行任意運算，那么，我們稱這種函數類型為Monad。Monad是一種高級別的思維抽象。

3.1 什么是Monad？

先思考一個問題，下面兩個定義有什么區別？

圖 45

num1是數字類型，而num2是對象類型，這是一個直觀的區別。

不過，不僅僅如此。利用類型，我們可以做更多的事。因為作為數字的num1是支持加減乘除運算的，而num2卻不行，必須要把它視為一個對象{val: 2}，并通過屬性訪問符num2.val才能進行計算num2.val + 2。但我們知道，函數式編程是不能改變狀態的，現在為了計算num2.val被改變了，這不是我們期望的，并且我們使用屬性操作符去讀數據，更像是在操作對象，而不是操作函數，這與我們的初衷有所背離。

現在我們把num2當作一個獨立的數據，并假設存在一個方法fmap可以操作這個數據，可能是這樣的。

圖 46

得到的還是對象，但操作通過一個純函數addOne去實現了。

上面這個例子里面的Num，實際上就是一個最簡單的Monad，而fmap是屬于Functor（函子）的概念。我們說函數就是從一個數據到另一個數據的映射，這里的fmap就是一個映射函數，在范疇論里面叫做態射（后面講解）。

由于有一個包裹的過程，很多人會把Monad看作是一個盒子類型。但Monad不僅是一個盒子的概念，它還需要滿足一些特定的運算規律（后面涉及）。

但是我們直接使用數字的加減乘除不行嗎？為什么一定要Monad類型？

首先，fmap的目的是把數據從一個類型映射到另一個類型，而JavaScript里面的map函數實際上就是這個功能。

圖 47

我們可以認為Array就是一個Monad實現，map把Array類型映射到Array類型，操作仍然在數組范疇，數組的值被映射為新的值。如果用TypeScript來表示，會不會更清晰一點？

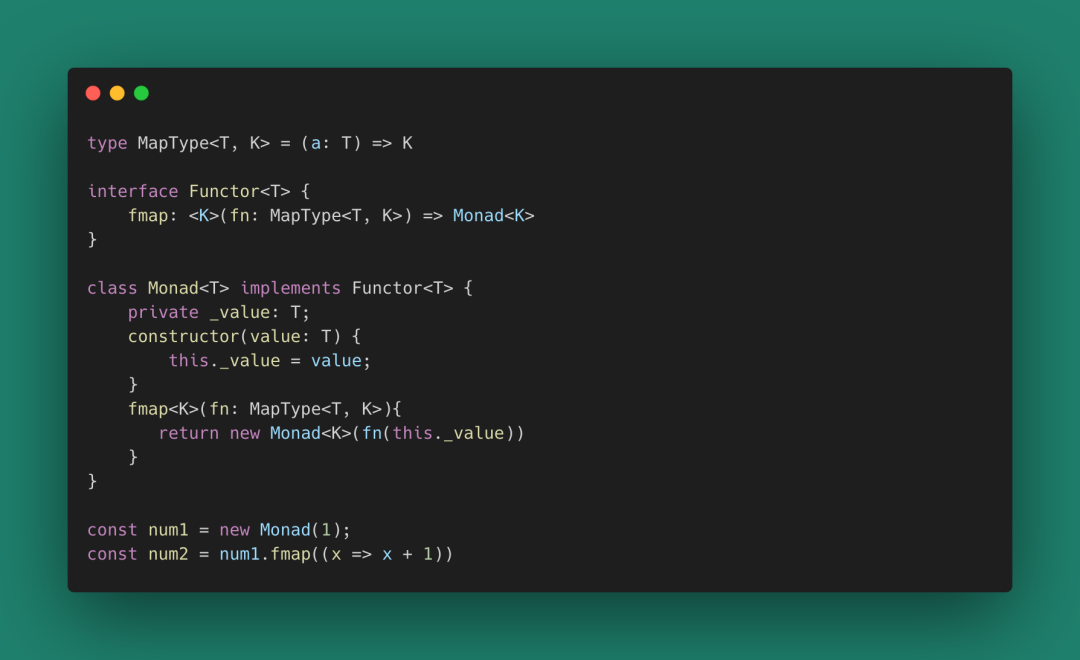
圖 48

看起來Monad只是一個實現了fmap的對象（Functor類型，mappable接口）而已。但Monad類型不僅是一個Functor，它還有很多其他的工具函數，比如：

bind函數

flatMap函數

liftM函數

這些概念在學習Haskell時可以遇到，本文不作過多提及。這些額外的函數可以幫助我們操作被封裝起來的值。

3.2 范疇、群、幺半群

范疇論是一種研究抽象數學形式的科學，它把我們的數學世界抽象為兩個概念：

對象

態射

為什么說這是一種形式上的抽象呢？因為很多數學的概念都可以被這種形式所描述，比如集合，對集合范疇來說，一個集合就是一個范疇對象，從集合A到集合B的映射就是集合的態射，再細化一點，整數集合到整數集合的加減乘操作構成了整數集合的態射（除法會產生整數集合無法表示的數字，因此這里排除了除法）。又比如，三角形可以被代數表示，也可以用幾何表示、向量表示，從代數表示到幾何表示的運算就可以視為三角形范疇的一種態射。

總之，對象描述了一個范疇中的元素，而態射描述了針對這些元素的操作。范疇論不僅可以應用到數學科學里面，在其他科學里面也有一些應用，實際上，范疇論就是我們描述客觀世界的一種方式（抽象形式）。

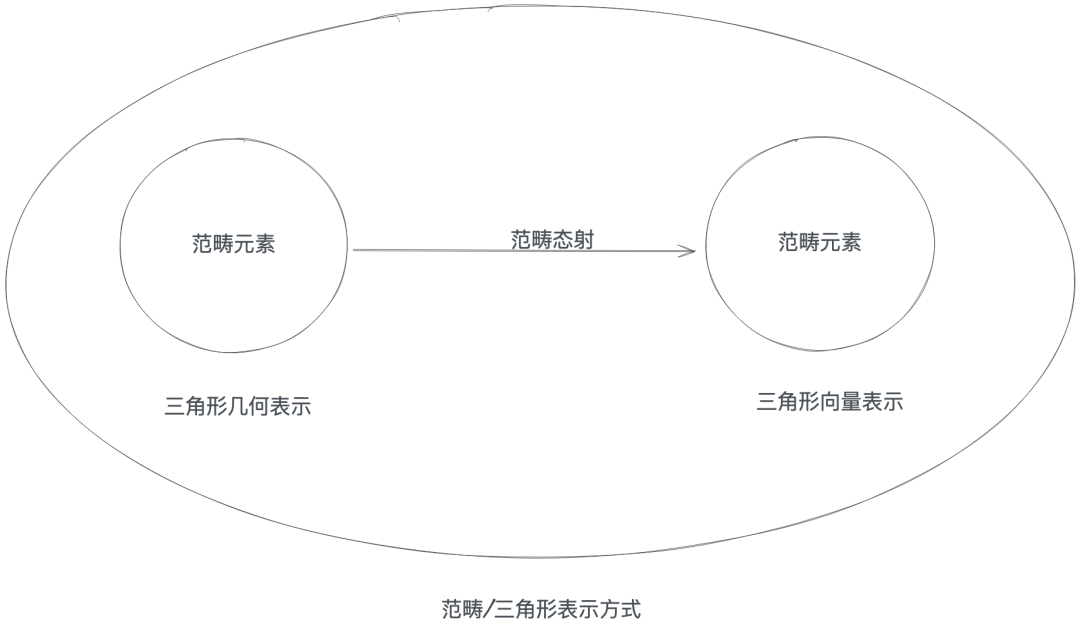
圖 49

相對應的，函子就是描述一個范疇對象和另一個范疇對象間關系的態射，具體到編程語言中，函子是一個幫助我們映射一個范疇元素（比如Monad）到另一個范疇元素的函數。

群論（Group）研究的是群這種代數結構，怎么去理解群呢？比如一個三角形有三個頂點A/B/C，那么我們可以表示一個三角形為ABC或者ACB，三角形還是這個三角形，但是從ABC到ACB一定是經過了某種變換。這就像范疇論，三角形的表示是范疇對象，而一個三角形的表示變換到另一個形式，就是范疇的態射。而我們說這些三角形表示方式的集合為一個群。群論主要是研究變換關系，群又可以分為很多種類，也有很多規律特性，這不在本文研究范圍之內，讀者可以自行學習相關內容。

科學解釋一個Monad為自函子范疇上的幺半群。如果沒有學習群論和范疇論的話，我們是很難理解這個解釋的。

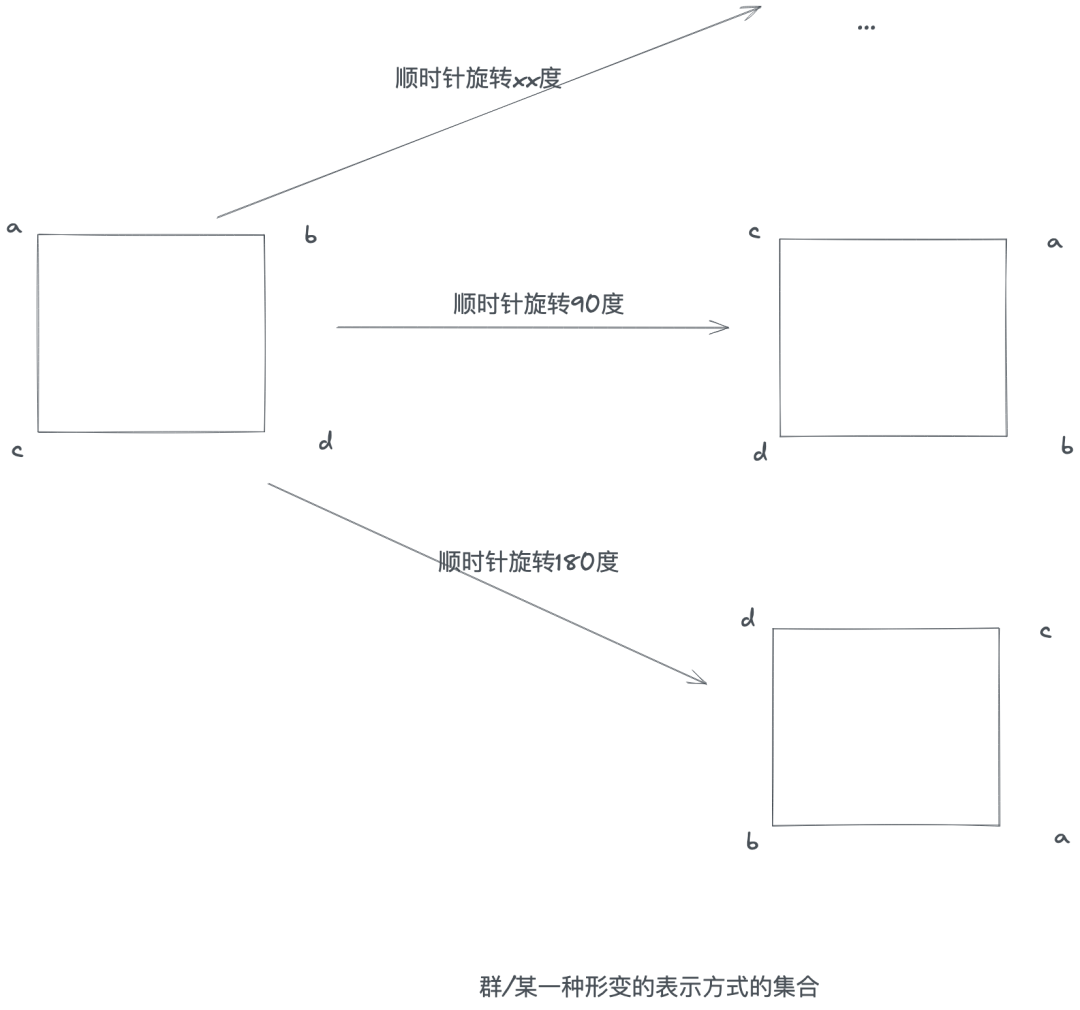
圖 50

簡單來說先固定一個正方形abcd，它和它的幾何變換方式（旋轉/逆時針旋轉/對稱/中心對稱等）形成的其他正方形一起構成一個群。從這個角度來說，群研究的事物是同一類，只是性質稍有不一樣（態射后）。

另外一個理解群的概念就是自然數（構成一個群）和加法（群的二元運算，且滿足結合律，半群）。

圖 51

到此，我們可以理解Monad為：

滿足自函子運算（從A范疇態射到A范疇，fmap是在自己空間做映射）。

滿足含幺半群的結合律。

很多函數式編程里面都會實現一個Identity函數，實際就是一個幺元素。比如JavaScript中對Just滿足二元結合律可以這么操作：

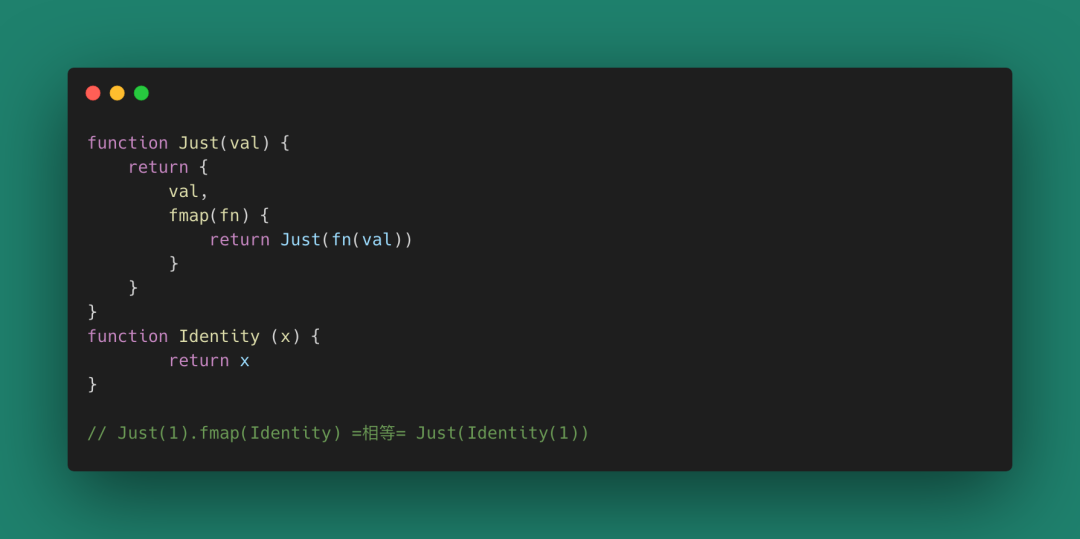
圖 52

3.3 Monad范疇：定律、折疊和鏈

我們要在一個更大的空間上討論這個范疇對象（Monad）。就像Number封裝了數字類型，Monad也封裝了一些類型。

圖 53

Monad需要滿足一些定律：

結合律：比如a · b · c = a · (b · c)。

幺元：比如a · e = e · a = a。

一旦定義了Monad為一類對象，fmap為針對這種對象的操作，那么定律我們可以很容易證明：

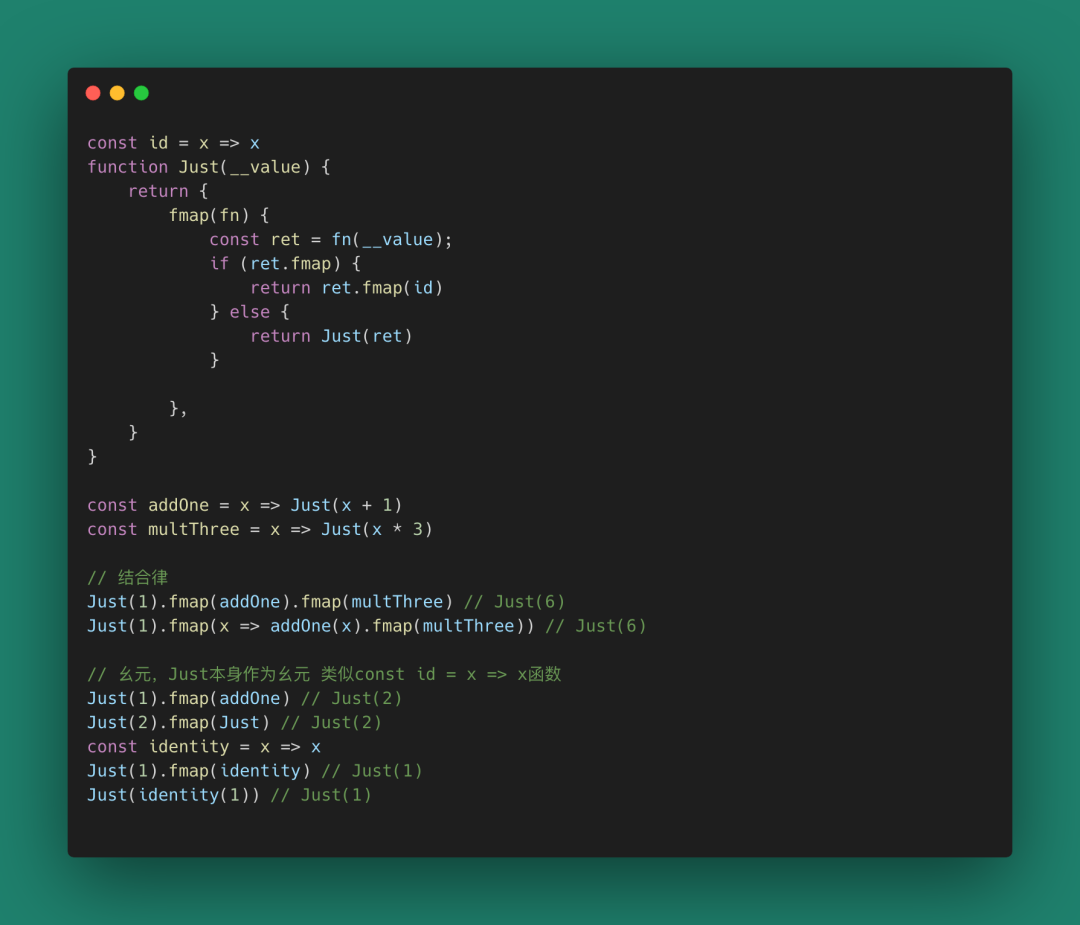
圖 54

我們可以通過Monad Just上掛載的操作來對數據進行計算，這些運算是限定在了Just上的，也就是說你只能得到Just(..)類型。要獲取原始數據，可以基于這個定義一個fold方法。

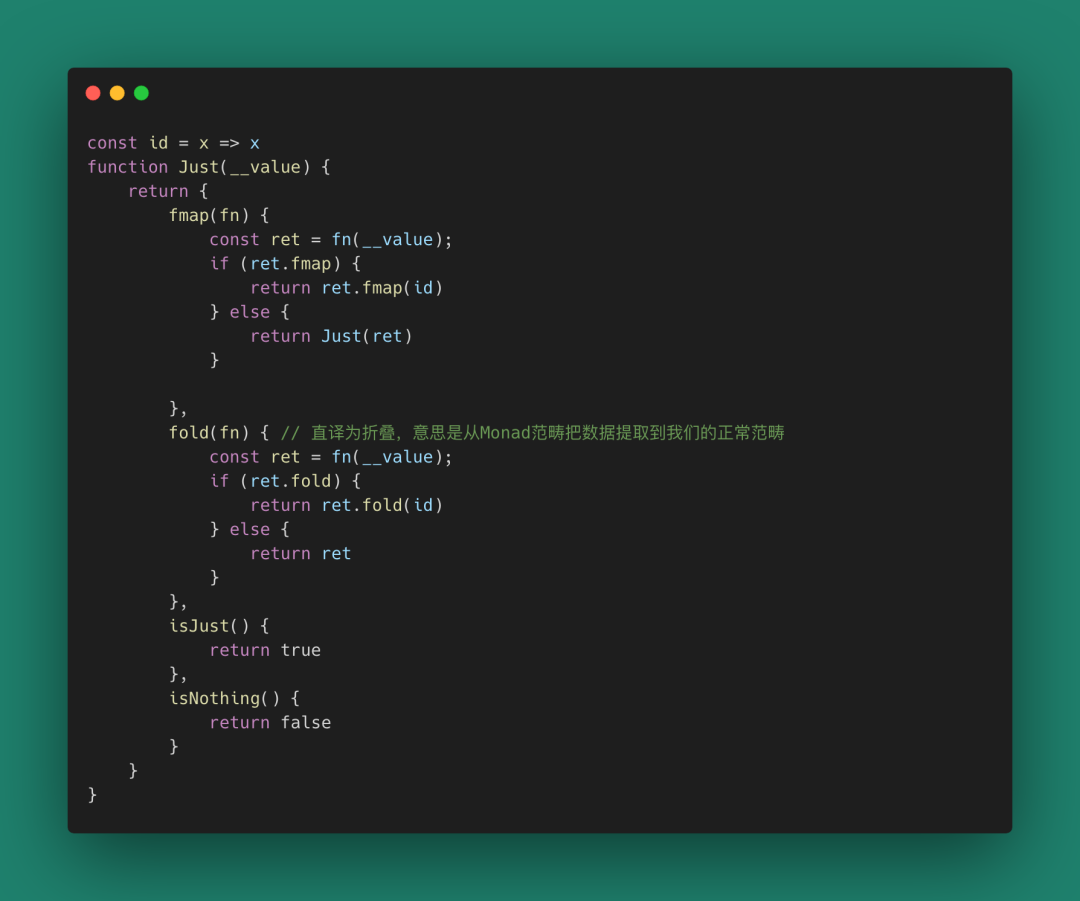
圖 55

fold（折疊，對應能力我們稱為foldable）的意義在于你可以將數據從一個特定范疇映射到你的常用范疇，比如面向對象語言的toString方法，就是把數據從對象域轉換到字符串域。

JavaScript中的Array.prototype.reduce其實就是一個fold函數，它把數據從Array范疇映射到其他范疇。

一旦數據類型被我們鎖定在了Monad空間（范疇），那我們就可以在這個范疇內連續調用fmap（或者其他這個空間的函數）來進行值操作，這樣我們就可以鏈式處理我們的數據。

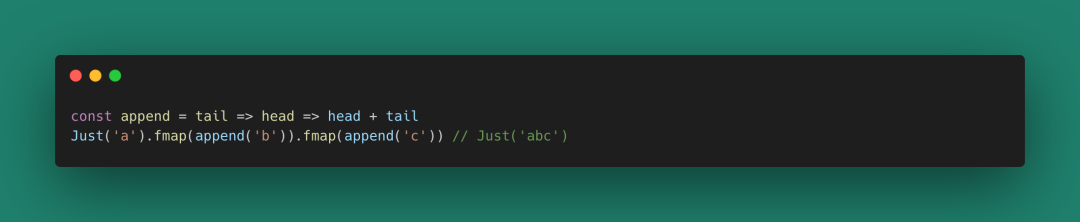
圖 56

3.4 Maybe和Either

有了Just的概念，我們再來學習一些新的Monad概念。比如Nothing。

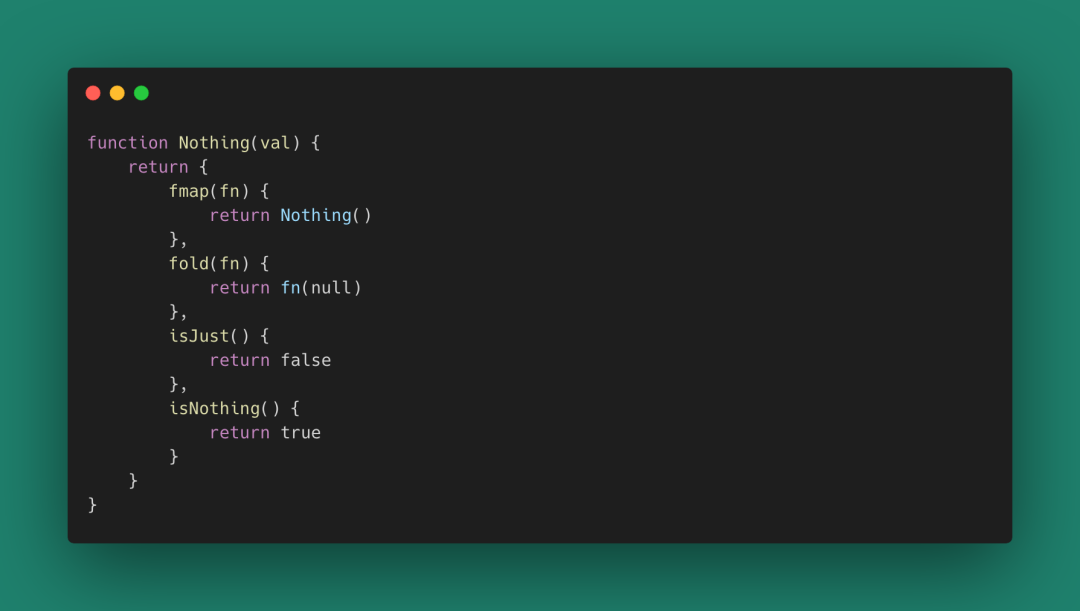
圖 57

Nothing表示在Monad范疇上沒有的值。和Just一起正好描述了所有的數據情況，合稱為Maybe，我們的Maybe Monad要么是Just，要么是Nothing。這有什么意義呢？

其實這就是模擬了其他范疇內的“有”和“無”的概念，方便我們模擬其他編程范式的空值操作。比如：

圖 58

這種情況下我們需要去判斷x和y是否為空。在Monad空間中，這種情況就很好表示：

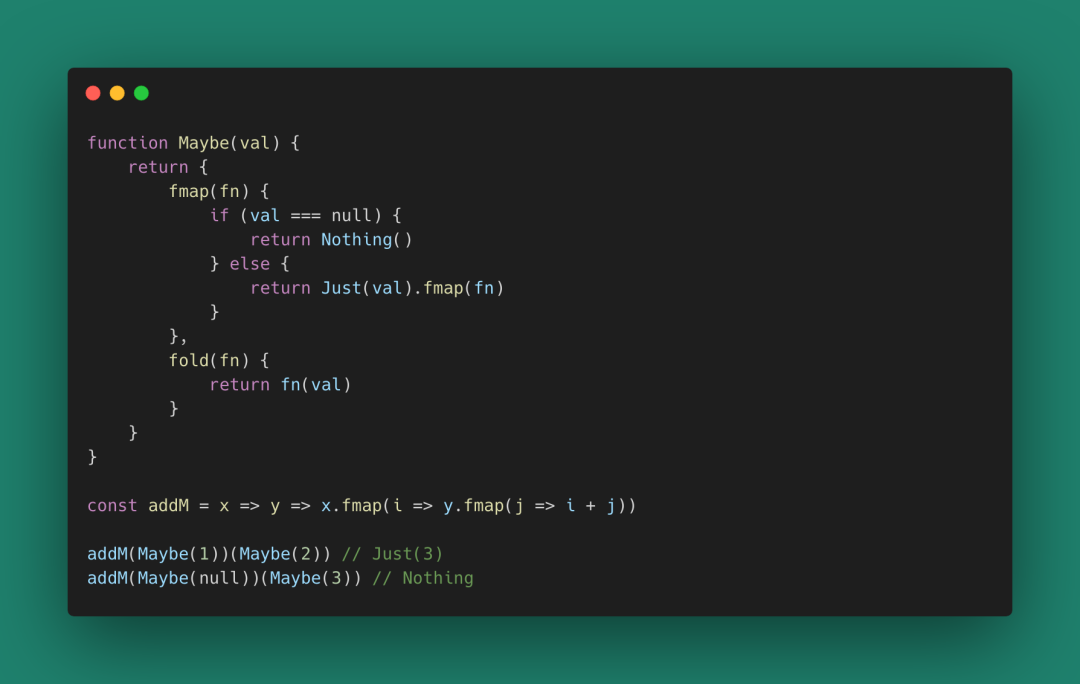
圖 59

我們在Monad空間中消除了煩人的!== null判斷，甚至消除了三元運算符。一切都只有函數。實際使用中一個Maybe要么是Just要么是Nothing。因此，這里用Maybe(..)構造可能讓我們難以理解。

如果非要理解的話，可以理解Maybe為Nothing和Just的抽象類，Just和Nothing構成這個抽象類的兩個實現。實際在函數式編程語言實現中，Maybe確實只是一個類型（稱為代數類型），具體的一個值有具體類型Just或Nothing，就像數字可以分為有理數和無理數一樣。

除了這種值存在與否的判斷，我們的程序還有一些分支結構的方式，因此我們來看一下在Monad空間中，分支情況怎么去模擬？

圖 60

假設我們有一個代數類型Either，Left和Right分別表示當數據為錯誤和數據為正確情況下的邏輯。

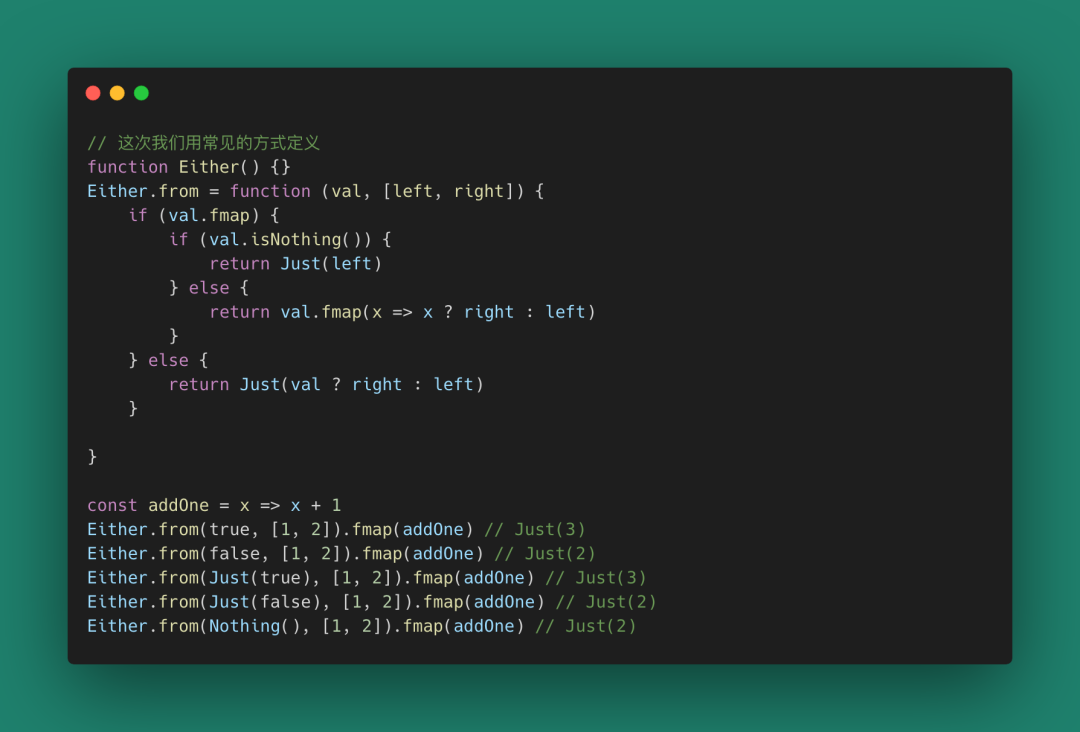
圖 61 這樣，我們就可以使用“函數”來替代分支了。這里的Either實現比較粗糙，因為Either類型應該只在Monad空間。這里加入了布爾常量的判斷，目的是好理解一些。其他的編程語言特性，在函數式編程中也能找到對應的影子，比如循環結構，我們往往使用函數遞歸來實現。

3.5 IO的處理方式

終于到IO了，如果不能處理好IO，我們的程序是不健全的。到目前為止，我們的Monad都是針對數據的。這句話對也不對，因為函數也是一種數據（函數是第一公民）。我們先讓Monad Just能存儲函數。

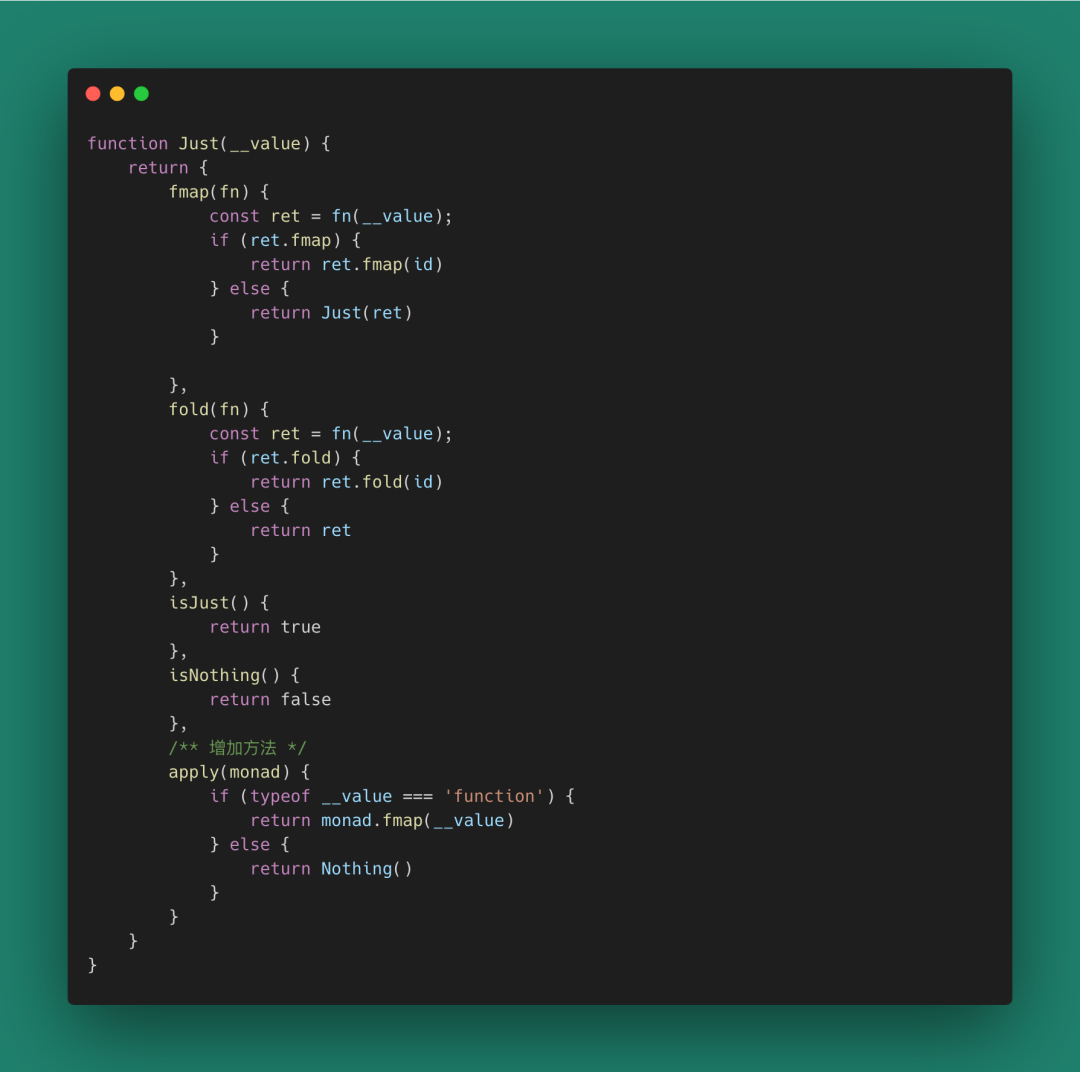
圖 62

你可以想象為Just增加了一個抽象類實現，這個抽象類為：

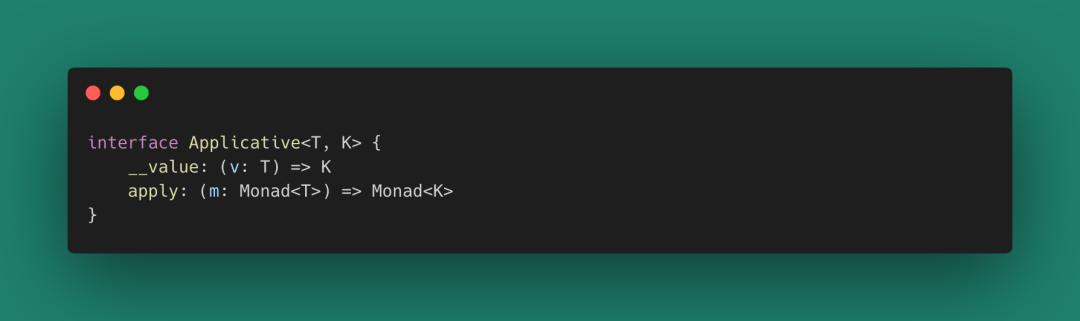
圖 63

這個抽象類我們稱為“應用函子”，它可以保存一個函數作為內部值，并且使用apply方法可以把這個函數作用到另一個Monad上。到這里，我們完全可以把Monad之間的各種操作（接口，比如fmap和apply）視為契約，也就是數學上的態射。

現在，如果我們有一個單子叫IO，并且它有如下表現：

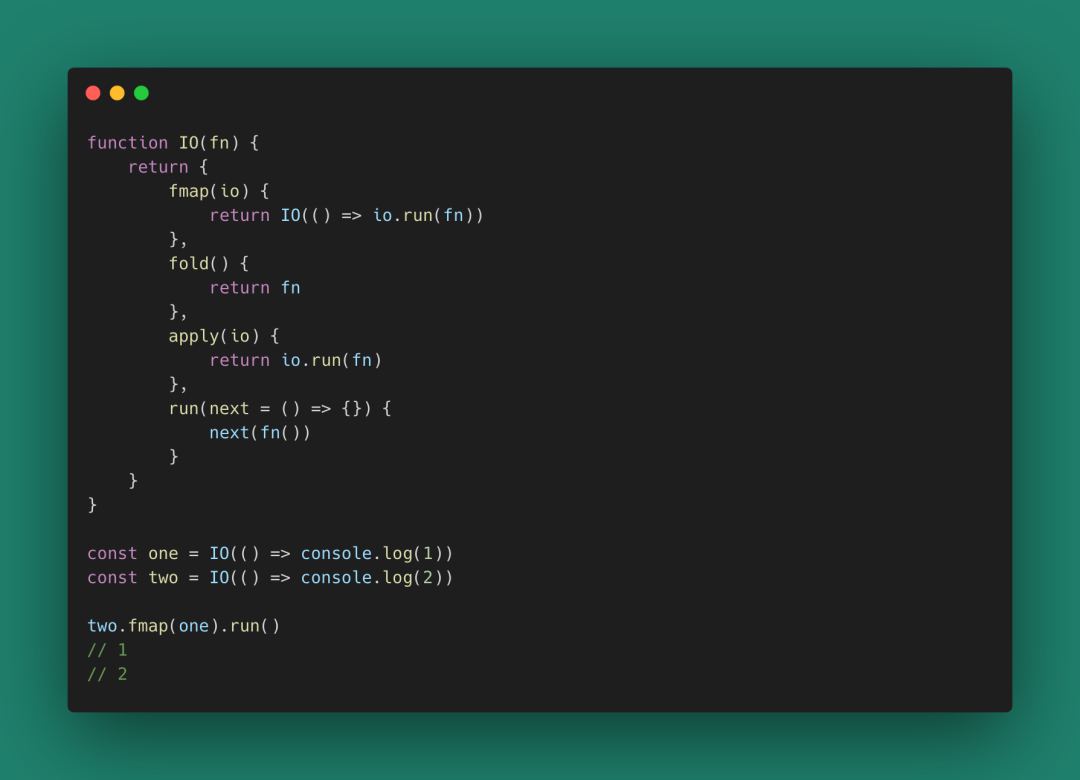
圖 64

我們把這種類型的Monad稱為IO，我們在IO中處理打印（副作用）。你可以把之前我們學習到的類型合并一下，得到一個示例：

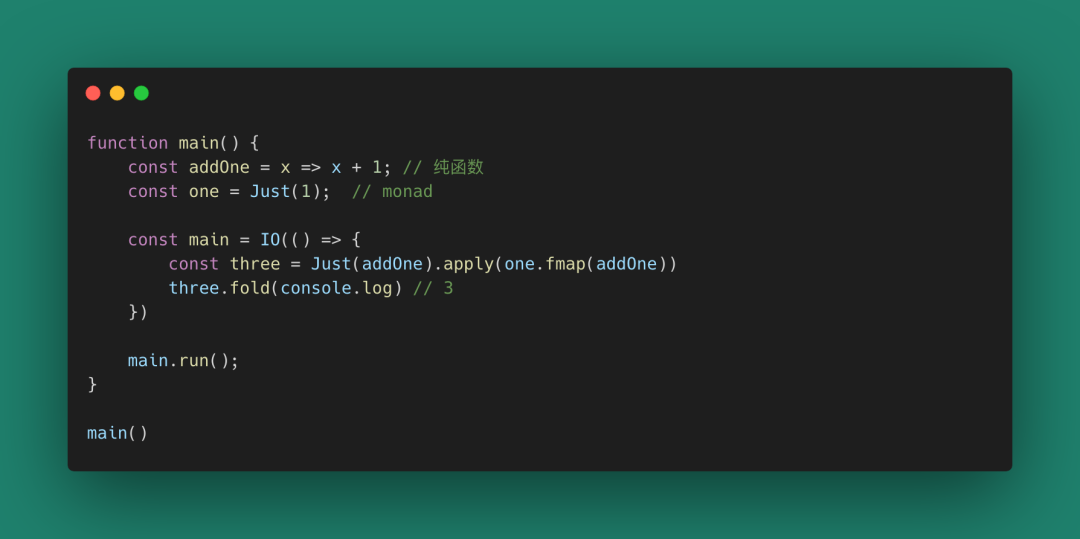
圖 65

通常一個程序會有一個主入口函數main，這個main函數返回值類型是一個IO，我們的副作用現在全在IO這個范疇下運行，而其他操作，都可以保持純凈（類型運算）。

IO類型讓我們可以在Monad空間處理那些煩人的副作用，這個Monad類型和Promise（限定副作用到Promise域處理，可鏈式調用，可用then折疊和映射）很像。

4. 函數式編程的應用

除了上面我們提到的一些示例，函數式編程可以應用到更廣的業務代碼開發中，用來替代我們的一些基礎業務代碼。這里舉幾個例子。

4.1 設計一個請求模塊

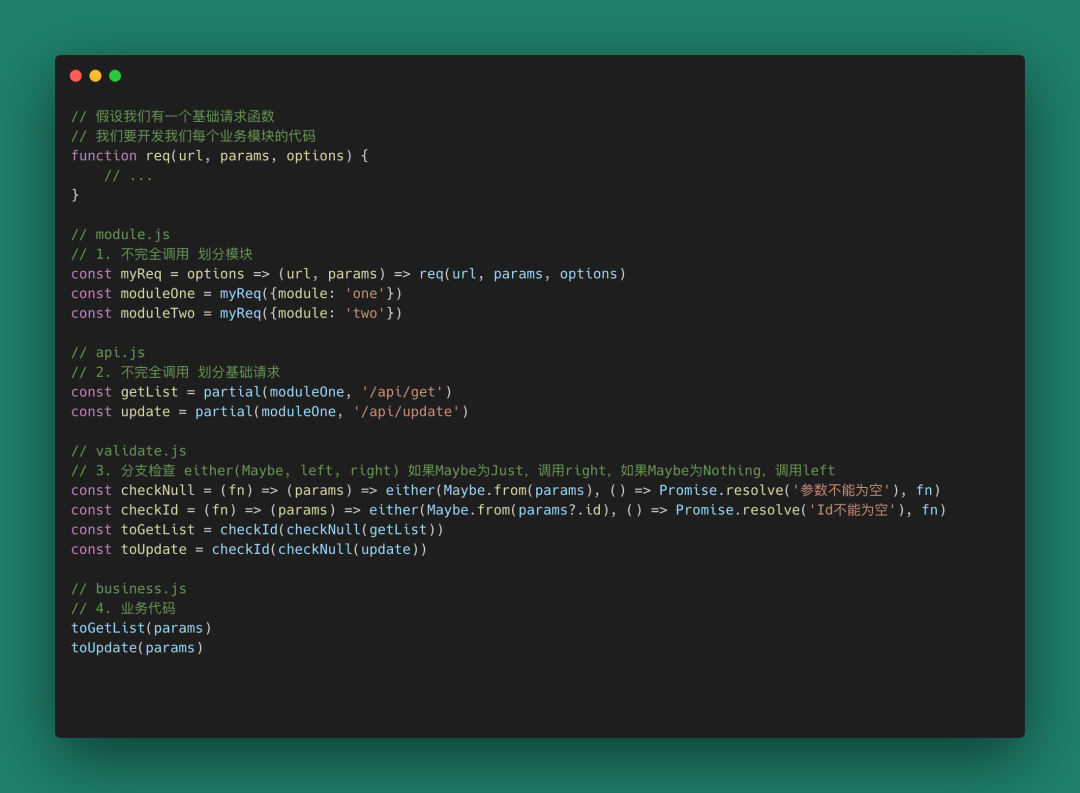
圖 66 用這種方式構建的模塊，組合和復用性很強，你也可以利用lodash的其他庫對req做一個其他改造。我們調用業務代碼的時候只管傳遞params，分支校驗和錯誤檢查就教給validate.js里面的高階函數就好了。

4.2 設計一個輸入框

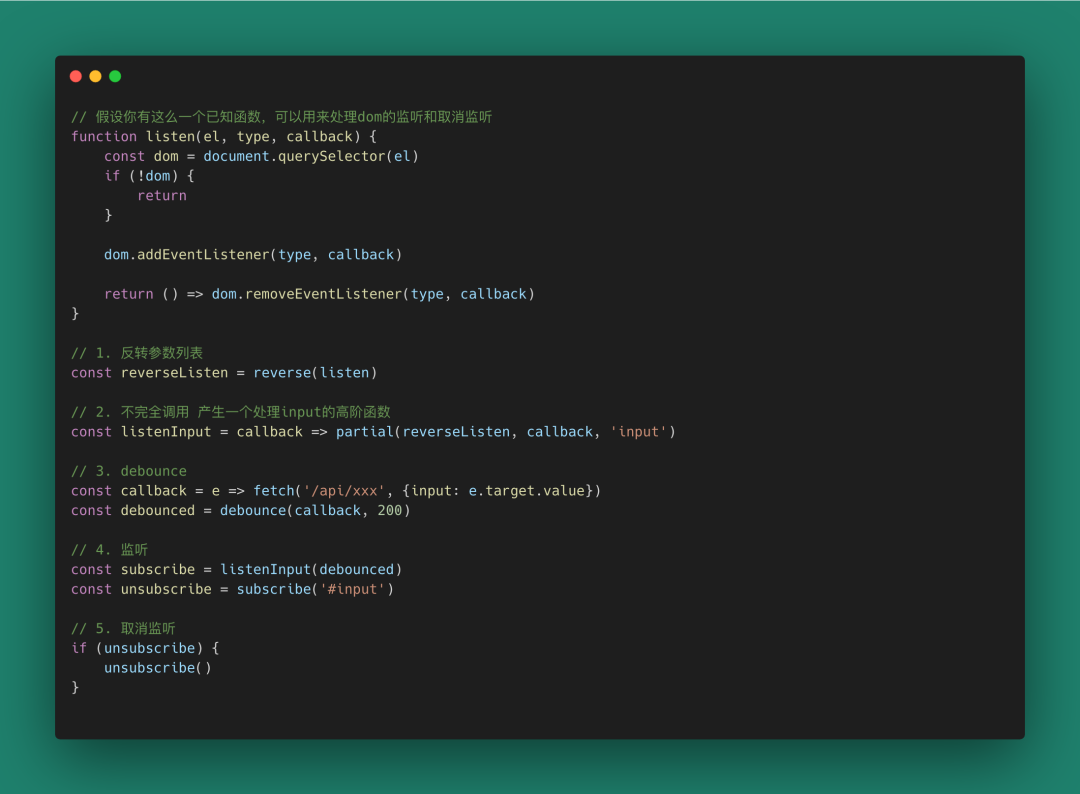
圖 67

這個例子也是來源于前端常見的場景。我們使用函數式編程的思想，把多個看似不相關的函數進行組合，得到了業務需要的subscribe函數，但同時，上面的任意一個函數都可以被用于其他功能組合。比如callback函數可以直接給dom回調，listenInput可以用于任意一個dom。

這種通過高階組件不停組合得到最終結果的方式，我們可以認為就是函數式的。（盡管它沒有像上一個例子一樣引入IO/Monad等概念）

4.3 超長文本省略：Ramdajs為例

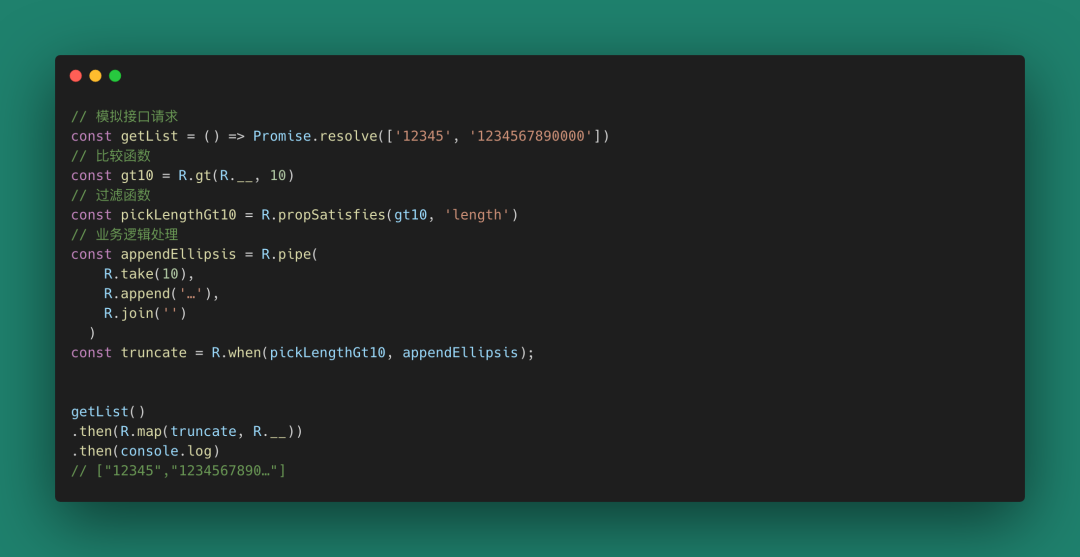
圖 68 這個也是常見的前端場景，當文本長度大于X時，顯示省略號，這個實現使用Ramdajs。這個過程中你就像是在搭積木，很容易就把業務給“搭建”完成了。

5. 函數式編程庫、語言

函數式編程的庫可以學習：

Ramda.js：函數式編程庫

lodash.js：函數工具

immutable.js：數據不可變

rx.js：響應式編程

partial.lenses：函數工具

monio.js：函數式編程工具庫/IO庫

...

你可以結合起來使用。下面是Ramda.js示例：

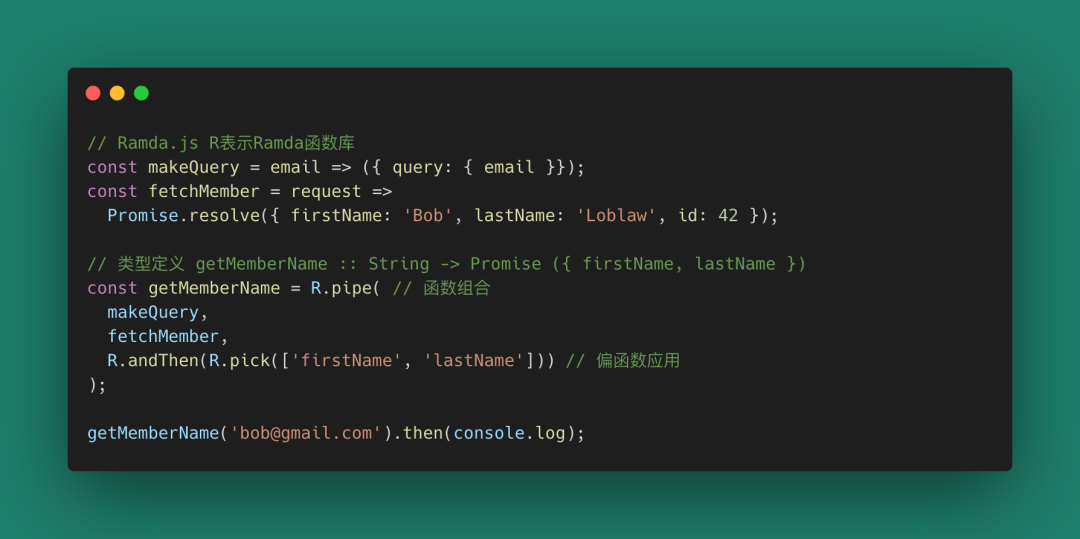
圖片69

而純函數式語言，有很多：

Lisp 代表軟件 emacs...

Haskell 代表軟件 pandoc...

Ocaml ...

...

6. 總結

函數式編程并不是什么“黑科技”，它已經存在的時間甚至比面向對象編程更久遠。希望本文能幫助大家理解什么是函數式編程。

現在我們來回顧先覽，實際上，函數式編程也是程序實現方式的一種，它和面向對象是殊途同歸的。在函數式語言中，我們要構建一個個小的基礎函數，并通過一些通用的流程把他們粘合起來。舉個例子，面向對象里面的繼承，我在函數式編程中可以使用組合compose或者高階函數hoc來實現。

盡管在實現上是等價的，但和面向對象的編程范式對比，函數式編程有很多優點值得大家去嘗試。

6.1 優點

除了上面提到的風格和特性之外，函數式編程相對其他編程范式，有很多優點：

函數純凈 程序有更少的狀態量，編碼心智負擔更小。隨著狀態量的增加，某些編程范式構建的軟件庫代碼復雜度可能呈幾何增長，而函數式編程的狀態量都收斂了，對軟件復雜度帶來的影響更小。

引用透明性 可以讓你在不影響其他功能的前提下，升級某一個特定功能（一個對象的引用需要改動的話，可能牽一發而動全身）。

高度可組合 函數之間復用方便（需要關注的狀態量更少），函數的功能升級改造也更容易（高階組件）。

副作用隔離 所有的狀態量被收斂到一個盒子（函數）里面處理，關注點更加集中。

代碼簡潔/流程更清晰 通常函數式編程風格的程序，代碼量比其他編程風格的少很多，這得益于函數的高度可組合性以及大量的完善的基礎函數，簡潔性也使得代碼更容易維護。

語義化 一個個小的函數分別完成一種小的功能，當你需要組合上層能力的時候，基本可以按照函數語義來進行快速組合。

惰性計算 被組合的函數只會生成一個更高階的函數，最后調用時數據才會在函數之間流動。

跨語言統一性 不同的語言，似乎都遵從類似的函數式編程范式，比如Java 8的lambda表達式，Rust的collection、匿名函數；而面向對象的實現，不同語言可能千差萬別，函數式編程的統一性讓你可以舒服地跨語言開發。

關鍵領域應用 因為函數式編程狀態少、代碼簡潔等特點，使得它在交互復雜、安全性要求高的領域有重要的應用，像Lisp和Haskell就是因上一波人工智能熱而火起來的，后來也在一些特殊的領域（銀行、水利、航空航天等）得到了較大規模的應用。

...

6.2 不足

當然，函數式編程也存在一些不足之處：

陡峭的學習曲線 面向對象和命令式編程范式都是貼近我們的日常習慣的方式，而函數式編程要更抽象一些，要想更好地管理副作用，你可能需要學習很多新的概念（響應式、Monad等），這些概念入門很難，而且是一個長期積累的過程。

可能的調用棧溢出問題 惰性計算在一些電腦或特種程序架構上可能有函數調用棧錯誤（超長調用鏈、超長遞歸），另外許多函數式編程語言需要編譯器支持尾遞歸優化（優化為循環迭代）以得到更好的性能。

額外的抽象負擔 當程序有大量可變狀態、副作用時，用函數式編程可能造成額外的抽象負擔，項目開發周期可能會延長，這時可能用其他抽象方式更好（比如OOP）。

數據不變性的問題 為了數據不變，運行時可能會構建生成大量的數據副本，造成時間和空間消耗更大，拖慢性能；同時數據不可變性可能會造成構建一些基礎數據結構的時候語法不簡潔，性能也更差（比如LinkedList、HashMap等數據結構）。

語義化的問題 往往為了開發一個功能，去造許多的基礎函數，大量業務組件想要語義化的命名，也會帶給開發人員很多負擔；并且功能抽象能力因人而異，公共函數往往不夠公用或者過度設計。

生態問題 函數式編程在工業生產領域因其抽象性和性能帶來的問題，被許多開發者拒之門外，一些特定功能的解決方案也更小眾（相比其他編程范式），生態也一直比較小，這成為一些新的開發人員學習和使用函數式編程的又一個巨大障礙。

...

日常業務開發中，往往我們需要取長補短，在適合的領域用適合的方法/范式。大家只要要記住，軟件開發并沒有“銀彈”。

7. FAQ

Q：你覺得Promise是不是一種Monad IO模型？

A：我認為是的。純函數是沒有異步概念的，Promise用了一種很棒的方式把異步和IO轉化為了.then函數。你仍然可以在.then函數中寫純粹的函數，也可以在.then函數中調用其他的Promise，這就和IO Monad的行為非常像。

Q：你愿意在生產中使用Haskell/Lisp/Clojure等純函數式語言嗎？

A：不論是否愿意使用，現在很多語言都開始引入函數式編程語法了。并不是說函數式編程一定是優秀的，但它至少沒有那么恐怖。有一點可以肯定的是，學習函數式編程可以擴展我們的思維，增加我們看問題的角度。

Q：有沒有一些可以預見的好處？

A：有的。比如強制你寫代碼的時候去關注狀態量（多少、是否引用值、是否變更等），這或多或少可以幫助你寫代碼的時候減少狀態量的使用，也慢慢地能復合一些狀態量，寫出更簡潔的代碼。

Q：函數式編程能給業務帶來什么好處？

A：業務拆分的時候，函數式的思維是單向的，我們會通過實現，想到它對應需要的基礎組件，并遞歸地思考下去，功能實現從最小粒度開始，上層逐步通過函數組合來實現。相比于面向對象，這種方式在組合上更方便簡潔，更容易把復雜度降低，比如面向對象中可能對象之間的相互引用和調用是沒有限制的，這種模式帶來的是思考邏輯的時候思維會發散。

這種對比在業務復雜的情況下更加明顯，面向對象必須要優秀的設計模式來實現控制代碼復雜度增長不那么快，而函數式編程大多數情況下都是單向數據流+基礎工具庫就減少了大量的復雜度，而且產生的代碼更簡潔。

8. 作者簡介

俊杰，美團到家研發平臺/醫藥技術部前端工程師。

審核編輯：湯梓紅