物理研究所面對的各種問題，其復(fù)雜性也與日俱增。個中邏輯，從一個問題是不是具有嚴格解的視角去看待，感受會很強烈。考慮凝聚態(tài)中眾所周知的“簡單”模型，如磁性 Ising 模型，其復(fù)雜性就是空間維度的強烈依賴函數(shù)。一維模型嚴格解，很早就被當時的博士生 Ising 輕松完成。到了二維，最簡單的正方格子模型嚴格解，乃多年后 Onsager 費九牛二虎之力方才成就。三維模型留到了今天，依然未解。這樣強烈的維度依賴，在幾乎所有物理模型中都是如此：如果將先輩們?nèi)局高^的所有固體物理模型統(tǒng)計起來，估計已有一維解的那些模型中，95% 以上都還沒有三維解。圖 1 給出一種意象的表達，展示量子凝聚態(tài)物理的一些簡單模型圖像。它們有些在特定條件下可解，但大多數(shù)無嚴格解。

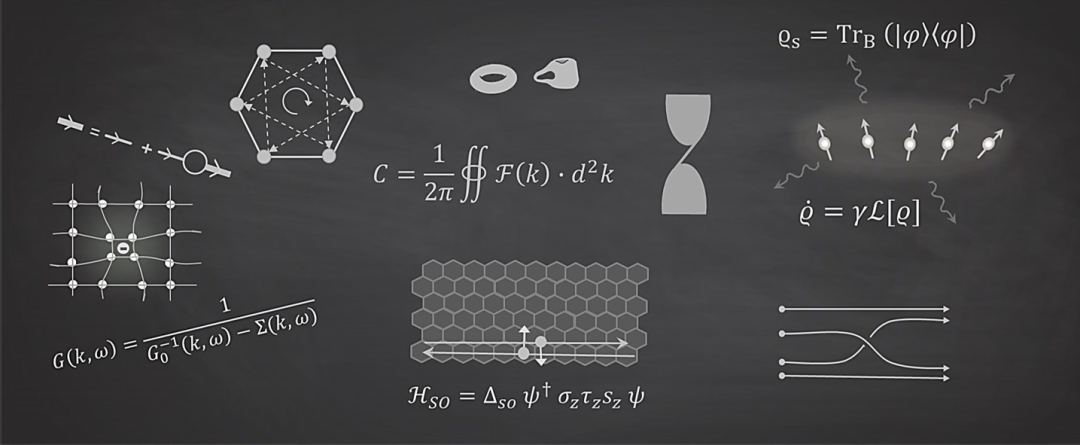
圖 1. 量子凝聚態(tài)物理中若干模型的圖像。

類似的問題，也可以拿體系基元數(shù)來進行討論。問題的復(fù)雜性，當然更強烈依賴于基元數(shù)目。簡單的三體問題，其運動學和動力學穩(wěn)定性就已經(jīng)不那么容易嚴格解構(gòu)了，更別去談多體問題。不過，與維度引致復(fù)雜性稍有不同，這里的復(fù)雜度，也許并非基元數(shù)的單調(diào)函數(shù)。當基元數(shù)趨向無窮大時，也有經(jīng)典熱力學這樣的非凡學問存在，可用連續(xù)化模式處理問題。因為熱力學就是關(guān)注大數(shù)系統(tǒng)連續(xù)化的學問，所以它代表了研究范式的變革，并非可以到處推廣的。事實上，我們見到最多的、也最令人具有挫折感的，是那些基元數(shù)目不多不少的中間區(qū)段：少，不足以單一離散化處理；多，不足以集成連續(xù)化處理；卻是這個不多不少，才令人抓狂矣。

以凝聚態(tài)物理為例，雖然過去幾十年也開始關(guān)注維度 (低維體系) 和小基元數(shù) (納米體系) 問題，但其主體和核心則針對不同對稱性的周期晶格而展開。從動能 + 勢能構(gòu)成的兩項哈密頓開始，從嚴格求解波函數(shù)或布里淵區(qū)能帶開始，到哈密頓中包含額外的相互作用項，不斷循序漸進。一路披荊斬棘的過程，既苦不堪言、也樂不思味。很顯然，哪怕是多一項，例如多一項不能忽略的非周期項，哈密頓求解的復(fù)雜性就立刻登峰造極，基本宣告哈密頓嚴格解的終結(jié)。圖 2 展示了這種復(fù)雜性的某種意象，由此可見，凝聚態(tài)結(jié)構(gòu)的花哨和復(fù)雜圖樣已經(jīng)有點令人無所適從。這樣的復(fù)雜性，在量子凝聚態(tài)和量子材料領(lǐng)域也很突出。其中關(guān)注的哈密頓，包括了一些缺乏長程周期性的相互作用項，沒有多少機會可以追逐嚴格求解 (包括全域嚴謹計算)。這一領(lǐng)域的物理基礎(chǔ)，大都是通過各種近似、提取物理問題的核心而構(gòu)建的。

及至今天，物理人是這樣認識量子凝聚態(tài)對象的：電子展示了電荷、自旋、軌道三個自由度，再加上晶格的若干可變參量 (幸虧晶格自由度具有某種周期對稱性)，組成了一個能量基元數(shù)不多不少的多體體系，對應(yīng)的哈密頓作用項也多了起來。這里，讀者可能會質(zhì)疑：既然如此，那何不另起爐灶？就像熱力學那樣，基于實驗和推理，重構(gòu)新的物理。這里的問題，看起來如前所述：體系相互作用項數(shù)目說多不多、說少不少。所謂左右逢源，這里則是左右都不沾。此時，實驗探索也遭遇到邏輯上的挑戰(zhàn)：一個諸如 4 維或 6 維的問題，能夠?qū)?yīng)的實驗架構(gòu)和能夠遍歷的實驗坐標空間，都是極其龐大的，要一一實驗訪問，幾乎不可能完成。至此，我們終于可以理解量子材料人，理解他們?yōu)楹螘酒鋵W術(shù)領(lǐng)域的艱辛和高度：這不是求安慰和仰望，而是真的富有挑戰(zhàn)和值得仰望！他們必須面對的、苦想冥思到鬢霜的，都是乍一看幾乎束手無策的、包含了N項的哈密頓。

這里，不妨以過渡金屬氧化物這一量子材料的最大類別為出發(fā)點，來具體化描述。量子材料人苦思冥想并身體力行的結(jié)果是：一個體系，大致上可以在電子動能項 (帶寬 W)、電子關(guān)聯(lián)項 U 和自旋 - 軌道耦合 SOC (λ) 項組成的三角形中找到自己的坐標，如圖 3 所示。我們姑且稱此三角形為“量子材料三角形”。當然，還有若干其它相對弱一些的基元項，作為簡化處理之需而被近似掉了。

在這個三角形中，3d 過渡金屬氧化物多在 U 比較大的一側(cè)，若干重費米子體系也歸屬此區(qū)，以 Mott 物理為典型代表。在那個區(qū)域，可以不用太過重視 SOC 的作用，哈密頓少了最難處理的一項，問題變得容易很多。說 SOC 項難處理，不只是因為它包含了自旋叉乘矩、包含了非共線自旋結(jié)構(gòu) (if any)。與此不同，4d 和 5d 過渡金屬氧化物，則會向三角形 SOC 那一側(cè)挪移 (不是貼近)，SOC 的作用變得顯著起來。另外，這些體系，因為離子實外軌道較為擴展，能帶帶寬 W 也相對較大，而關(guān)聯(lián) U 相對弱化 (但不可忽略)。也就是說，4d / 5d 過渡金屬化合物這類體系，妥妥地位于量子材料三角形的中心區(qū)，并同時對影響 W、U 和 SOC 的內(nèi)外激勵都有敏感響應(yīng)。凝聚態(tài)物理最難的區(qū)域，暴露于我們視野之下！

對這類復(fù)雜體系，靠實驗探索，成效的確較低，雖然高水準的實驗永遠是結(jié)論對錯的最終試金石，其地位不可或缺。個中原因至少有兩點：(1) 4d / 5d 家族成員本就不多，實驗的可控參數(shù)與不可控參數(shù)不相伯仲，因此設(shè)計實驗以掌控體系狀態(tài)的機會不大。(2) 回顧研究歷程，正是這種復(fù)雜性、敏感性和可控性的挑戰(zhàn)，使得 4d / 5d 過渡金屬化合物的研究，相比于那些 3d 體系研究，呈現(xiàn)弱勢，雖然也有 University ofColorado at Boulder 曹鋼老師這樣的杰出代表。

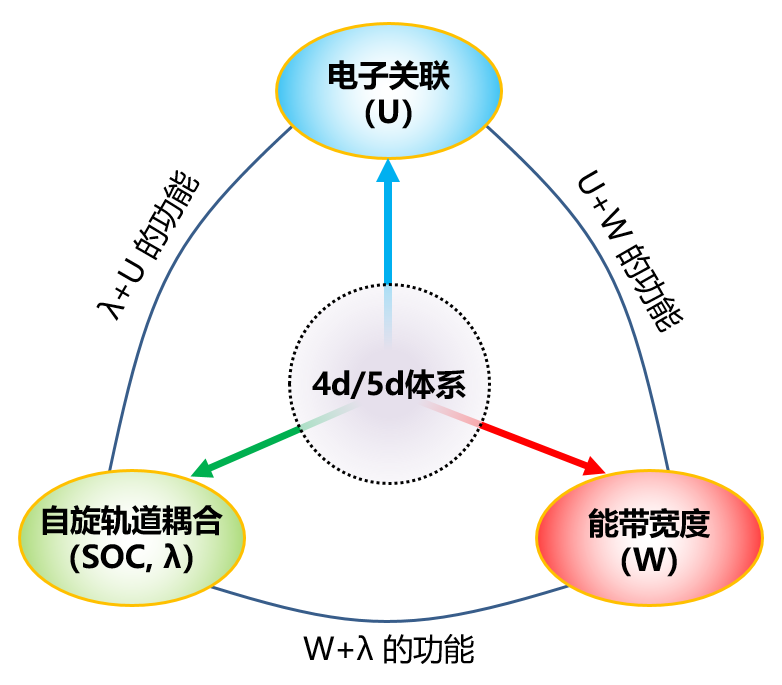
圖 3. 量子材料三角形 (陸成亮教授版權(quán)所有)。其中每一角都是相對簡單可解的物理，但組合起來，則復(fù)雜無尚。

舉個具體實例，以避免總是說空話。5d 過渡金屬氧化物中的銥氧化物 (Ir - based oxides)，就是集 (W, U, SOC) 于一身的量子材料小家庭。為了簡潔起見，以具有 Jeff = 1/2電子結(jié)構(gòu)特征的Sr2IrO4 (SIO) 為對象，進行復(fù)雜性的具體羅列：

(1) 屬于 214 的 SIO，與同屬 214 的 Sr2CuO4，一直都被寄予厚望會對高溫超導物理產(chǎn)生重要貢獻。Sr2CuO4乃典型的Mott體系，但 SIO 似乎不是。例如，希望載流子摻雜可以導致 SIO 超導的實驗嘗試一直未能成功，體現(xiàn)了復(fù)雜性。

(2) 對 Mott 絕緣體體系，諸多理論計算和實驗嘗試都揭示，壓力會誘發(fā) MIT 絕緣體 - 金屬相變，對應(yīng)的磁結(jié)構(gòu)也會發(fā)生轉(zhuǎn)變。對 3d 體系，此一物理屢試不爽，但用到 SIO 上就不成功。據(jù)說等靜壓實驗已經(jīng)加到 200 GPa 了，依然還是一幅不典型絕緣體、不典型金屬的樣子，體現(xiàn)了復(fù)雜性。對其它銥氧化物如 Sr3Ir2O7，也是如此狀況：要得到金屬特征，可是艱難。

(3) SIO 是很有特色的準二維結(jié)構(gòu)氧化物。一些二維物理，包括異質(zhì)結(jié)二維電子氣和低維載流子輸運，在其中也能找到蹤跡。

(4) 晶格結(jié)構(gòu)畸變對 SIO 的電子結(jié)構(gòu)和輸運行為也展示了前所未有的影響。特別是伴隨而生的電子軌道畸變，影響最近鄰、次近鄰、及至次次近鄰的相互作用強弱及磁性。

這四個層面的影響，不能說在其它過渡金屬氧化物中就沒有。但是，正因為 SIO 位于量子材料三角形中心，這些影響都集成于一體，讓我們有些手足無措。于是，開始有量子材料人致力于放大招，以嘗試全域計算來解決問題。來自還很年輕的奧地利研究機構(gòu)“奧地利科技研究院 (Instituteof Science and Technology Austria, ISTA)”的 Ekaterina M. P?rschke 博士，聯(lián)合來自米國亞拉巴馬大學的Cheng-Chien Chen教授團隊 (The University of Alabama at Birmingham, https://www.uab.edu/cas/physics/people/faculty/cheng-chien-chen) 等，最近在《npj QM》上刊登文章，報道了他們對 SIO 在面內(nèi)雙軸可控應(yīng)變作用下的計算結(jié)果。他們的工作，顯著推進了對銥氧化物磁性、輸運及結(jié)構(gòu)演化的多維度認識，形成如下認知：

(1) 因為體系依然是 Mott 絕緣體，為了描述電子關(guān)聯(lián)，必須考慮 Hubbard 模型。

(2) 因為體系位于量子材料三角形中心，也應(yīng)該考量軌道電子、SOC 和軌道 - 晶格耦合的貢獻，需要采用第一性原理計算方法。

(3) 因為體系對內(nèi)外激勵都高度敏感，應(yīng)變條件下可能出現(xiàn)的 MIT 物理不能忽略，因此需要構(gòu)建等效海森堡模型的哈密頓。

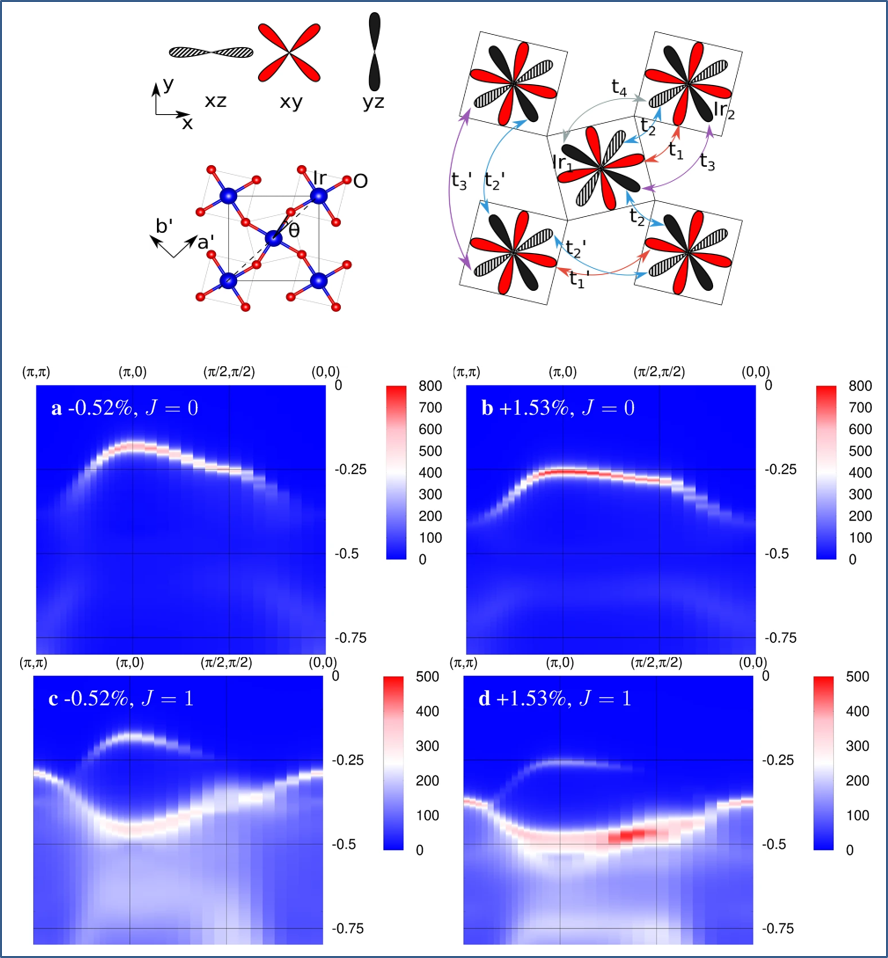
圖 4. P?rschke 博士他們構(gòu)建的 Sr2IrO4 結(jié)構(gòu)模型和計算所得電子能譜結(jié)構(gòu)。

P?rschke 博士他們采用的方法包括：(a) 第一性原理計算，以追蹤晶格結(jié)構(gòu)及其畸變，包括 Wannier 函數(shù)計算；(b) 包含自洽 Bohr 近似 SCBA 的擴展 t – J 模型數(shù)值計算，以與 ARPES 實驗得到的電子結(jié)構(gòu)能譜比對；(c) 等效海森堡模型哈密頓，以便于從計算結(jié)果比對擬合來獲取模型參數(shù)，實現(xiàn)無可變參數(shù)的全尺度計算。

他們的計算，揭示了一些有新意的結(jié)果，能合理解構(gòu)實驗觀測現(xiàn)象 (參見論文詳細描述)。在 ab面雙軸應(yīng)變情況下，他們的計算顯示：(1) 應(yīng)變改變了 Ir – Ir 鍵長和 Ir – O – Ir 鍵角，卻幾乎沒有影響 IrO6 氧八面體形狀本身，似乎符合實驗觀測到的結(jié)構(gòu)畸變特征。(2) 壓應(yīng)變下會形成面內(nèi)羅盤狀晶格畸變，導致軌道依賴的能帶特征，很是獨特。(3) 壓應(yīng)變下能帶色散增強、帶寬增大，面內(nèi) MIT 轉(zhuǎn)變可能發(fā)生。拉應(yīng)變下，平帶效應(yīng)顯著增強，給原本不大的關(guān)聯(lián) U 以彰顯強關(guān)聯(lián)效應(yīng)的機會。可以看到，這三點結(jié)果并非完全相長或相消，符合對 SIO 復(fù)雜量子效應(yīng)的預(yù)期。圖 4 所示為部分結(jié)果，其中細節(jié)可參考論文 (點擊文尾“閱讀原文”)。

這些全域自洽的電子結(jié)構(gòu)和等效模型集成計算，展示了理論上如何追蹤一個相互作用基元數(shù)目不多亦不少的固體電子體系、如何自洽解構(gòu)其中的結(jié)構(gòu)與功能變化。很顯然，基于量子材料三角形的不同位置，要實現(xiàn)實驗可觀測量的高精度計算，對理論計算工具及其集成的需求也有不同。這一追蹤，從 P?rschke 博士他們的工作看，似乎很有希望，雖然前路漫長。

審核編輯：郭婷