在許多工程應(yīng)用中，梁都是由彈性構(gòu)件進(jìn)行支承的，比如一些軸通常由滾珠、滾柱或軸頸軸承進(jìn)行支承，一些較大的梁由彈性墻進(jìn)行支承，還有一大類(lèi)梁支承在地基上，一般將這類(lèi)問(wèn)題稱為Winkler地基。

單排滾珠軸承可以看做是：在每個(gè)軸承處都有一個(gè)節(jié)點(diǎn)，并將軸承剛度加到單元?jiǎng)偠染仃囍袑?duì)應(yīng)垂直自由度的對(duì)角位置上（見(jiàn)圖1a）：而對(duì)于滾柱或軸頸軸承，還要考慮相應(yīng)的轉(zhuǎn)動(dòng)（力矩）剛度。 對(duì)于較寬的軸頸軸承和Winkler地基，我們使用支承介質(zhì)的單位長(zhǎng)度上的剛度s來(lái)描述（見(jiàn)圖1b）。在支承介質(zhì)所作用的長(zhǎng)度范圍內(nèi)，總勢(shì)能將會(huì)多出下面一項(xiàng)。

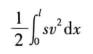（1）

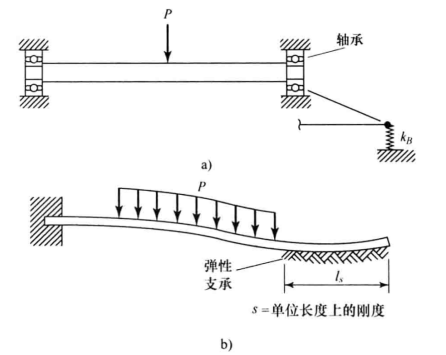
圖1 彈性支承 當(dāng)我們將代人離散化模型后，上式將變?yōu)?/p>

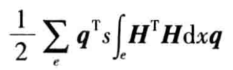
（2）

其中H為Hermite插值函數(shù)

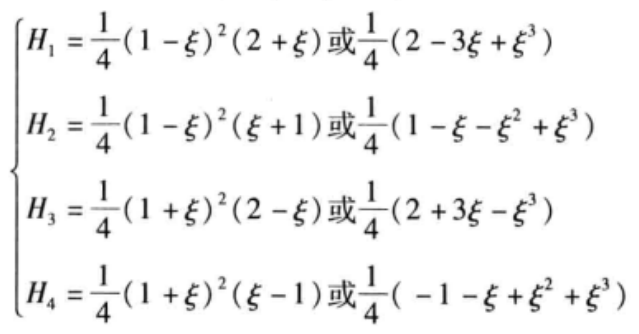
（3）

從公式（2）中的求和公式里，可以看出其中的單元?jiǎng)偠染仃図?xiàng)，即

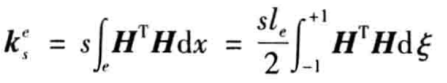
（4）

因?yàn)槌Ｒ?guī)的梁?jiǎn)卧獎(jiǎng)偠染仃囈彩峭ㄟ^(guò)最小勢(shì)能原理就行推導(dǎo)，對(duì)應(yīng)的單元應(yīng)變能和剛度矩陣的表達(dá)式為

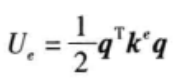（5）

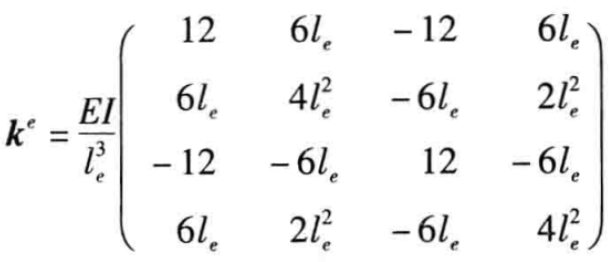
（6）

對(duì)公式（4）進(jìn)行積分之后，可得

（6）

對(duì)于具有彈性地基支撐的單元，這一剛度矩陣需要加入到公式（6）梁?jiǎn)卧獙?duì)應(yīng)的傳統(tǒng)的單元?jiǎng)偠染仃囍校?img alt="" border="0" height="38" src="https://file1.elecfans.com//web2/M00/97/A9/wKgaomTnM3aANlH_AAADNiARPSQ324.png" width="177" />。而矩陣就是彈性地基的一致剛度矩陣。 如果考慮到軸向變形，則為

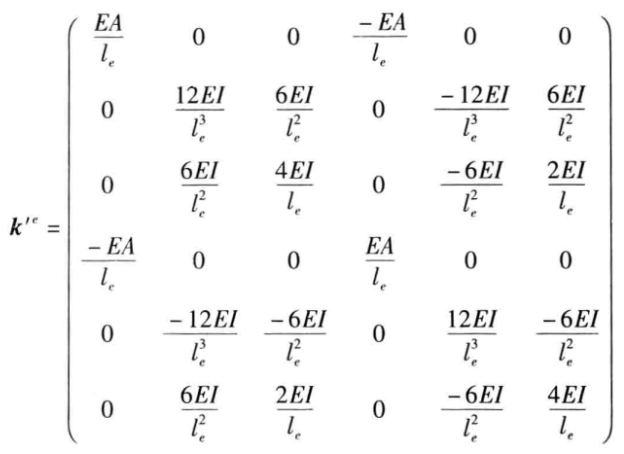
（6）

對(duì)應(yīng)的只需要用零元素?cái)U(kuò)充軸向自由度，因?yàn)榱旱膹澢洼S向變形不相互耦合。 這次課提供的彈性地基梁的有限元案例，是這種雙排樁支護(hù)結(jié)構(gòu)的matlab有限元編程計(jì)算分析。模型的計(jì)算簡(jiǎn)圖如圖2所示。

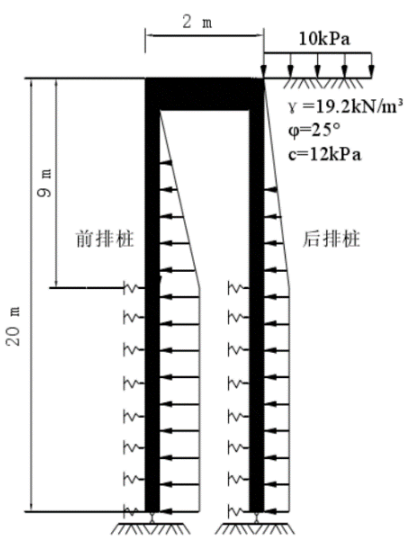
圖2 模型計(jì)算簡(jiǎn)圖 從結(jié)構(gòu)上分析，雙排樁支護(hù)結(jié)構(gòu)如同嵌入土中的門(mén)式剛架，與單排樁的懸臂結(jié)構(gòu)、多支點(diǎn)的混合支護(hù)結(jié)構(gòu)、重力式擋土結(jié)構(gòu)等支護(hù)形式的受力機(jī)理有明顯的差異。開(kāi)挖面下的樁體受到側(cè)向的地基抗力在模型中簡(jiǎn)化為土彈簧反力，樁底的約束由具體的土質(zhì)條件和計(jì)算模型來(lái)確定，綜合考慮上述幾個(gè)方面的問(wèn)題后，包括樁頂結(jié)點(diǎn)的處理，彈性地基梁?jiǎn)卧獎(jiǎng)偠染仃嚨拇_定以及荷載列陣的確定等，就可以建立基本的平衡方程求解樁身各結(jié)點(diǎn)位移和樁身內(nèi)力。 對(duì)于坑底下部的彈性地基梁?jiǎn)卧膭偠染仃嚦Ｒ?guī)方法是按集中剛度的原則先確定在單元結(jié)點(diǎn)處的等效彈簧剛度然后疊加到總剛。如果將上述計(jì)算的彈簧剛度按結(jié)點(diǎn)位置相應(yīng)的疊加到總剛那么只能加到總體剛度矩陣對(duì)角線元素上。 事實(shí)上這樣處理彈性地基梁?jiǎn)卧姆椒ú皇鞘趾侠怼Ｉ鲜龇椒ㄖ皇窃诮Y(jié)點(diǎn)設(shè)置彈簧沒(méi)有考慮到被動(dòng)區(qū)土壓力也是沿樁體連續(xù)分布的并不等效于各個(gè)集中彈簧力的作用并且等效剛度不是簡(jiǎn)單的將某個(gè)區(qū)域的剛度求和。為此本文提出一種思路就是考慮單元兩結(jié)點(diǎn)間布滿彈簧再將這些分布的彈簧反力轉(zhuǎn)化為等效結(jié)點(diǎn)力建立彈性地基梁?jiǎn)卧Y(jié)點(diǎn)力與結(jié)點(diǎn)位移的關(guān)系最終可得到基于一般梁?jiǎn)卧拚蟮膹椥缘鼗簡(jiǎn)卧獎(jiǎng)偠染仃嚕缦率剿荆?/p>

（7）

剛度矩陣具體推導(dǎo)過(guò)程請(qǐng)看論文《雙排樁開(kāi)挖過(guò)程的改進(jìn)有限元分析方法》。

本算例用到的基本參數(shù)

（1）土性指標(biāo)：土體粘聚力 c=12k Pa；內(nèi)摩擦角 φ=25°；土體重度 γ=19.2k N/m3。土體平均壓縮模量 Es=5MPa，不考慮地下水位的影響。采用單一的土層計(jì)算。

（2）基坑開(kāi)挖深度為 9.0m，前后排樁呈矩形布置，樁直徑為0.8m，樁彈性模量E1=3.0×107kN/m^2，樁間距為2m，前排樁入土深度為 11m，樁長(zhǎng)為 20m。

（3）連梁截面尺寸 b×h=800mm×600mm，連梁彈性模量 E2=3.0×107k N/ m^2，連梁之間的距離等于兩樁間距，兩排樁的排距為 2.0m，樁頂與連梁按剛接考慮。

（4）彈簧的反力系數(shù)，m=4000kN/m^3，樁底采用單鏈桿支承約束，以此替代樁土之間摩擦力的作用，水平向不約束。

（5）土壓力采用朗肯主動(dòng)土壓力計(jì)算，并考慮 10k Pa 的地面施工超載，坑底以上為三角形的分布，基坑底面以下為矩形分布。計(jì)算彈性地基梁的剛度矩陣相應(yīng)的代碼如下：

%計(jì)算彈性地基梁?jiǎn)卧獎(jiǎng)偠染仃嚭瘮?shù)
function [Ke] = FrameElementKe2(A,E,I,R,BarLength)
   global m D
   L=BarLength;
   k=m*D*L;
   k1=k;
   k2=k;
   ke=[E*A/L       0             0          -E*A/L       0                0
       0        12*E*I/L^3+4*k1*L/15+k2*L/12     6*E*I/L^2     0       -12*E*I/L^3+k1*L/12+k2*L/15   6*E*I/L^2;
       0        6*E*I/L^2+k1*L^2/30+k2

由于不同基坑開(kāi)挖深度為9m，所以九米以上的樁可以認(rèn)為傳統(tǒng)梁，九米以下的樁為彈性地基梁。因此在進(jìn)行單元?jiǎng)偠染仃囉?jì)算和組裝時(shí)要根據(jù)單元所在位置分別進(jìn)行計(jì)算和組裝，具體的matlab代碼如下：

%遍歷所有單元，將各單元?jiǎng)偠汝嚪謮K組裝到總體剛度陣
for iEle =1:EleCount
%該單元的兩個(gè)節(jié)點(diǎn)的編號(hào)
n1=ele(iEle,2);n2=ele(iEle,3);
%計(jì)算坐標(biāo)變換矩陣
R=CoordTransform([x(n1) x(n2)],[y(n1) y(n2)],BarLength(iEle));
%計(jì)算單元?jiǎng)偠染仃?Ke=R'*ke*R;局部坐標(biāo)系下的單元?jiǎng)偠汝囖D(zhuǎn)換為全局坐標(biāo)下的單元?jiǎng)偠汝?if y(n1)<=deep     
ke= FrameElementKe2(ele(iEle,4),ele(iEle,5),ele(iEle,6),R,BarLength(iEle));
else     
ke= FrameElementKe1(ele(iEle,4),ele(iEle,5),ele(iEle,6),R,BarLength(iEle));
end
%將各單元?jiǎng)偠确謮K組裝到總剛相應(yīng)位置
eleDof=[n1*3-2:n1*3,n2*3-2:n2*3];
K(eleDof,eleDof)=K(eleDof,eleDof)+ke; 
end

最終計(jì)算得到的前后排樁隨深度的撓度和彎矩分別如圖3所示，與文獻(xiàn)中的結(jié)果基本一致，另外本案例還對(duì)雙排樁支撐結(jié)構(gòu)的彎矩圖進(jìn)行繪制，如圖4所示。

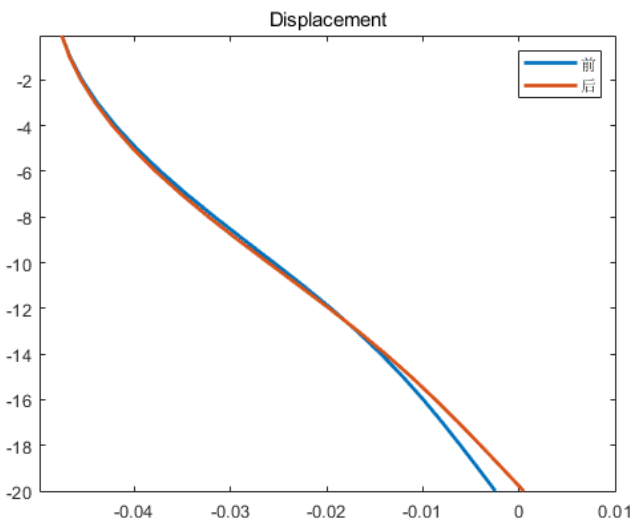
圖3 前后排樁不同深度處水平位移

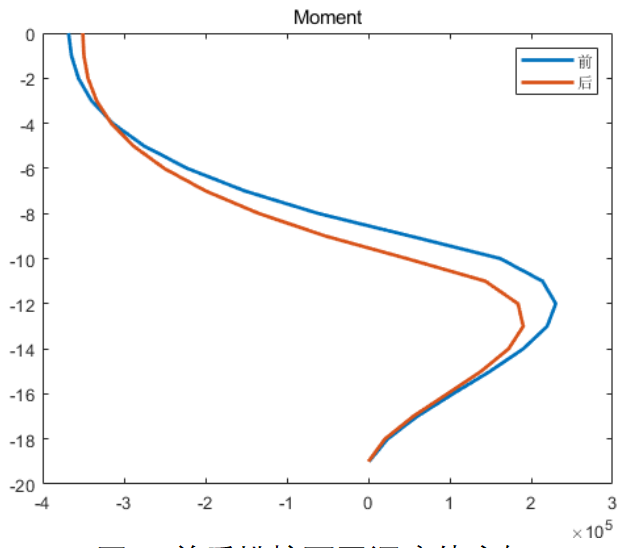
圖4 前后排樁不同深度處彎矩

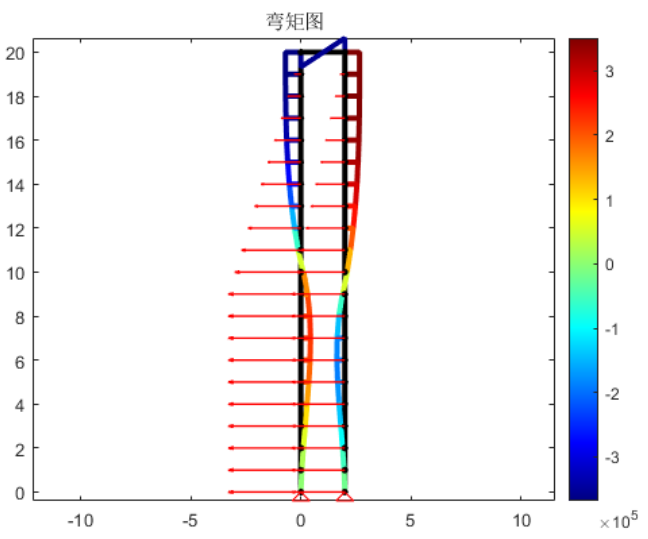
圖5 彎矩圖

審核編輯：郭婷