在看空間統計相關的文檔資料的時候,看到了幾個有關距離丈量方法的術語詞匯,諸如:歐式距離、曼哈頓距離、切比雪夫距離……老外習慣于使用名字來命名算法,可是對于門外漢們,是一種困惑,今天就整理下,一起溫故知新。
1. 歐式距離(EuclideanDistance)
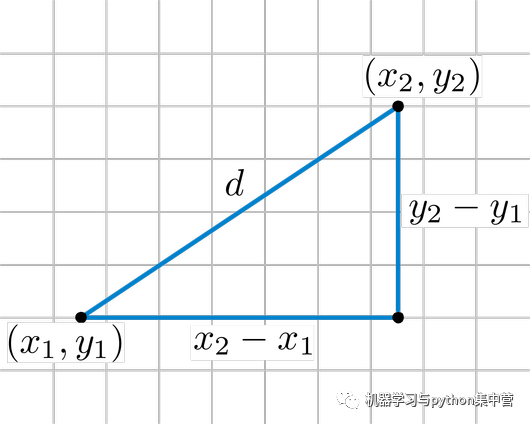
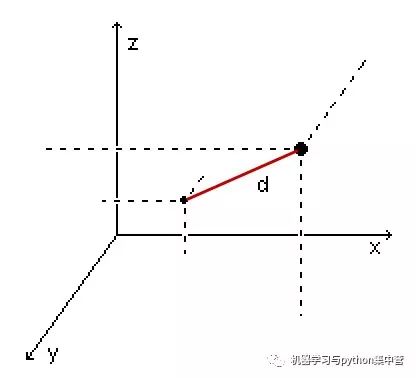
歐式距離是我們在直角坐標系中最常用的距離量算方法,例如小時候學的“兩點之間的最短距離是連接兩點的直線距離。”這就是典型的歐式距離量算方法。
通常這這個距離的獲取是基于我們熟悉的“勾股定理”,解算三角形斜邊得到的。
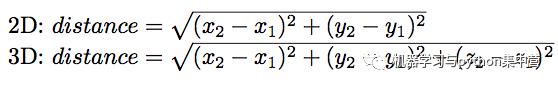
2. 曼哈頓距離(Manhattan Distance)
曼哈頓距離是與歐式距離不同的一種丈量方法,兩點之間的距離不再是直線距離,而是投影到坐標軸的長度之和。
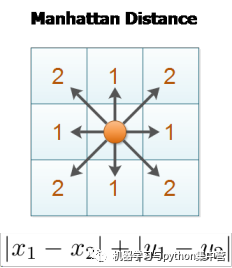
還是看圖吧,圖比文字更顯見。
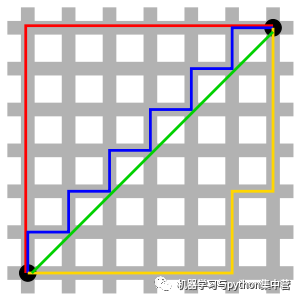
圖中綠色的線為歐式距離的丈量長度,紅色的線即為曼哈頓距離長度,藍色和黃色的線是這兩點間曼哈頓距離的等價長度。
想想我們下象棋的時候,車炮兵之類的,是不是要走曼哈頓距離?
如果不會下象棋,沒關系,看下面的例子:
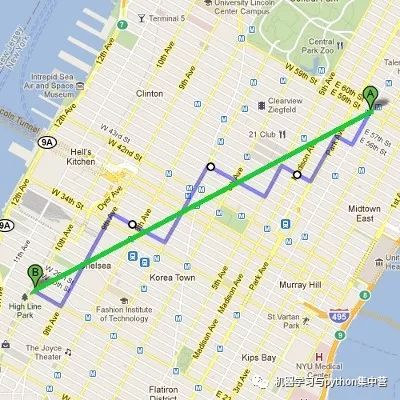
在美國道路會像這樣是很多的規則的網格狀,從A到B通常無法去沿直線行走,而是會避開建筑物,走幾個街區到達。
圖中藍色的線即為曼哈頓距離的典型應用場景。
3.切比雪夫距離(Chebyshev distance)
數學上,切比雪夫距離是將2個點之間的距離定義為其各坐標數值差的最大值。
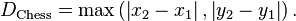
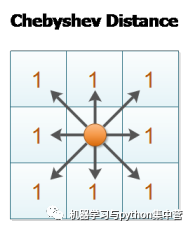
網上搜索,好多有關這個距離的解釋,大多都是采用國際象棋中的王的走步來作為例子,王可以前后左右走,還可以斜前斜后走,一共8個方向可以認為距離均等。
也就是在下面3×3鄰域內,中心網格的中心點到8個鄰域網格中心點的距離相等。

審核編輯 :李倩
-
算法
+關注
關注
23文章
4608瀏覽量
92845 -
距離
+關注
關注
0文章
12瀏覽量
13801
原文標題:歐式距離、曼哈頓距離、切比雪夫距離三種距離的可視化展示
文章出處:【微信號:vision263com,微信公眾號:新機器視覺】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
網線最遠傳輸距離多少
天線匹配對通信距離的影響實例

LORA模塊的通信距離是多少
基于 ToF 的 OPT3101 遠距離接近和距離傳感器 AFE數據表

接地距離保護有什么特點
接地距離保護和相間距離保護如何構成
爬電距離是根據什么確定的
多模光纖比單模光纖傳輸距離更遠的原因
網橋傳輸距離多遠?
基于ToF 的 OPT3101 遠距離接近和距離傳感器AFE數據手冊
安規距離設計簡介
如何估算光纜通信距離?





 歐式距離、曼哈頓距離、切比雪夫距離三種距離的可視化展示
歐式距離、曼哈頓距離、切比雪夫距離三種距離的可視化展示










評論