01
研究動機
數學問題(英文叫Math Word Problem,簡稱MWP)的求解要求給定一段描述文本,其中包含對于若干已知變量和一個未知變量的描述,要求利用變量間的數值關系來推理計算出未知變量的準確數值。
一個具體的例子如下圖1所示,可以發現一個數學問題可能對應著多個正確的表達式或二叉樹,有著非確定性的輸出空間,而目前主流方法輸入問題文本序列來學習特定單個表達式序列或二叉樹的生成,使得模型所學到的知識不完整,并需要大量數據來提升性能,限制了模型在低資源場景下的表現。
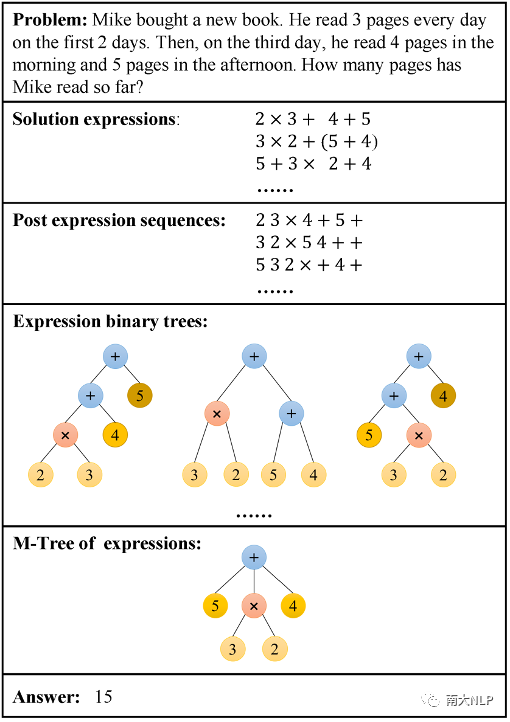
圖1: MWP問題示例
對于MWP的輸出多樣性,分析原因如下:
1、計算順序的不確定性:a)運算之間常擁有相同的計算優先級。如n1 + n2 + n3 ? n4 中的三個運算符優先級一樣,可以等價轉換為不同的序列或二叉樹;b)數學表達式中括號的使用給計算順序也帶來了不確定性。如n1 + n2 ? n3, n1 ? (n3 ? n2) 和 (n1+n2)?n3都是等價的表達;
2、運算的可交換性帶來的不確定性:加法和乘法操作兩邊的算子可以進行交換且不影響計算邏輯與最終結果,使得輸出的結構具有多樣性的表達,如n1 + n2 × n3可以轉換為n1+n3×n2,n2×n3+n1等;
為了解決由多樣性給問題求解帶來的挑戰,我們提出了基于結構統一M叉編碼樹的數學問題求解器。針對第一點原因,在二叉樹的結構基礎上,我們設計了擁有任意分支數量的M-tree,在豎直方向上對樹的結構進行統一;針對第二點,我們在M-tree中重新定義了新的M元運算,使得所有的運算都滿足可交換性,將只在子節點左右順序不一樣的兩棵M-tree視為相同的結構,從而在水平方向對樹的結構進行統一。
而為了學習輸出M-tree,我們放棄了進行自上而下且從左到右的自回歸式生成方法,因為該方法不能避免由于子節點左右順序的變化而帶來的輸出(one by one)多樣性。我們首先對M-tree進行編碼,將其轉換為M-tree codes形式的等價表達,用于保存M-tree的結構信息,其中每個code對應M-tree中的一個葉子節點,保存從根節點到葉子節點的路徑以及葉子節點本身的信息。
通過一個sequence to code(seq2code)模型學習從輸入問題文本序列到每個code的映射,以非自回歸的方式生成輸出。
02
貢獻
1、我們分析了MWP中輸出多樣性的原因,創新地設計了一個基于M樹的方案來統一輸出結構;
2、我們設計了M-tree codes來等價表示M-tree,并提出了一個seq2code模型來以非自回歸的方式生成codes,據我們所知這是第一個利用M-tree codes和seq2code來分析求解MWP的工作;
3、在廣泛使用的Math23K和MAWPS數據集上的實驗結果表明,SUMC-Solver在同等實驗設置下優于以前的方法。尤其是在低資源的情況下,我們的求解器取得了更好的性能表現。
03
解決方案
方法的整體示例及模型框架如下圖2所示,下面介紹M-tree,M-tree codes和seq2code模型的設計。
M-tree的設計:M-tree具有兩種節點——內部節點和葉子節點,其中內部節點擁有任意M個子分支(M>=1)且對應四種M元運算:{ +,x,x-,+/ },這四種M元運算都具有可交換性,葉子節點有四種:{原始數值v,v的負數,v的倒數,v的倒數的相反數};定義M-tree的根節點為+類型節點,任何兩棵僅在子節點左右順序不一樣的M-tree會被視為同一顆。
M-tree codes的設計:由于M-tree中的內部節點可以擁有任意數量的子分支,且兄弟節點在結構上的位置是等價的,所以基于自回歸式的生成不能避免由于兄弟節點的順序在輸出端造成的多樣性。為了解決這一難題,我們將M-tree的結構信息編碼到每個葉子節點中,在M-tree和葉子節點的codes集合之間形成一個映射,這樣模型就能以非自回歸的方式生成codes。
具體而言,每個葉子節點的M-tree code由兩部分組成:一部分保存數值信息,會使用兩個二進制位來區分數值的四種形式,另一部分由根節點到當前葉子節點的路徑信息構成。
seq2code模型框架:為了驗證M-tree和M-tree codes的先進性,我們設計了一個簡單的seq2code模型來求解MWP,它將問題文本序列作為其輸入,然后輸出問題中數值的相應code(以向量表示)。在結合所有的codes以恢復M-tree之后,我們可以計算出問題的最終答案。整個模型由兩部分組成:問題編碼器和code生成器。a)問題編碼器將MWP的單詞轉化為向量表示,我們的實驗中編碼器有兩種選擇:循環神經網絡(RNN)編碼器或預訓練語言模型(PLM)編碼器;b)我們使用了一個簡單的三層前饋神經網絡(FFNN)來作為生成器。
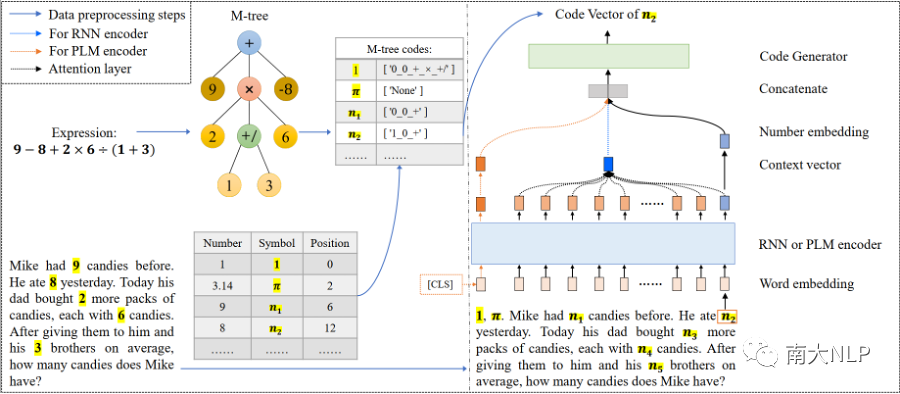 圖2:?SUMC-Solver問題求解示例與模型框架
圖2:?SUMC-Solver問題求解示例與模型框架
04
實驗
實驗結果展示在表1中。SUMC-Solver在兩個MWP數據集上的表現優于所有的基準模型。當使用RNN編碼器時,SUMC-Solver的準確率比學習表達式序列輸出的StackDecoder和T-RNN 高約9-10%。相比學習二叉樹輸出的方法,SUMC-Solver也取得了比GTS、SAU-Solver和Graph2Tree更好的結果,盡管這些方法使用了精心設計的樹解碼器或豐富輸入表示的圖編碼器。
當使用預訓練語言模型(PLM)作為編碼器時,SUMC-Solver達到了82.5%的準確率,比GTS-PLM和UniLM-Solver有了明顯的提高(分別為3%和5%)。總之,上述兩種不同編碼器設置下的結果都表明,M-tree和M-tree codes的設計是合理和先進的,這使得我們只用一個簡單的seq2code模型就可以達到更好的性能。
表1:各模型在基準數據集上的性能對比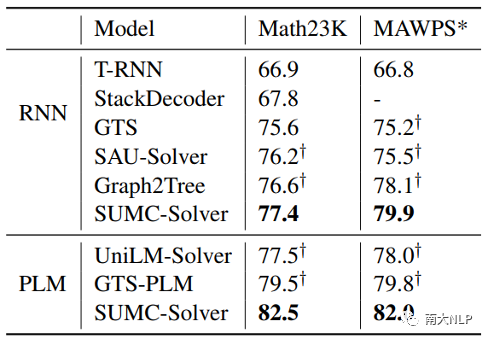
表1中在Math23K數據集上展示的是在公共測試集上的結果,在MAWPS*上展示的是5折交叉驗證的結果,帶 ? 的結果是由我們復現得到的。
MWP的人工標注成本很高,因此提升該模型在低資源場景下的表現是有必要的。我們用不同數據規模的訓練集來評估GTS、SAU-Solver和Graph2Tree的性能。測試集統一包含2,312個隨機抽樣的實例。詳細的結果可以在圖3中找到。可以看出,無論訓練集的大小如何,SUMC-Solver的性能始終優于其他模型。
首先,當訓練集的規模小于6000時,SAU-Slover的性能優于GTS;當數量超過6000時,這兩個模型的性能相似。就整體性能而言,在資源受限的情況下,SAU-Solver和Graph2Tree的結果比GTS的好。其次,在6000個樣本的訓練集下,SUMC-Solver和其他模型之間出現了最明顯的性能差距,我們的模型在準確率上大約提升了5%。這表明SUMC-Solver在低資源情況下具有突出的優勢。
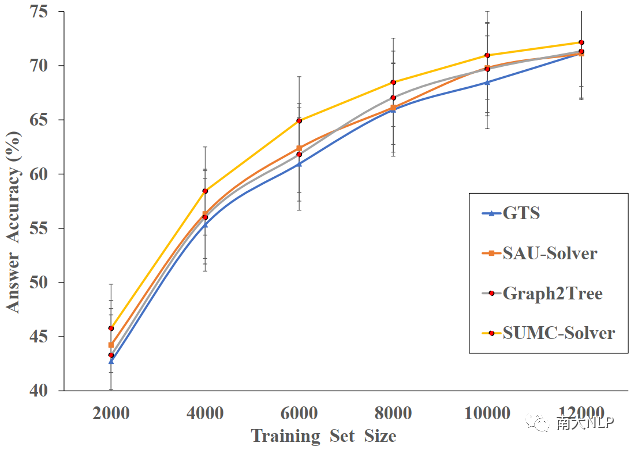
圖3:低資源場景下的模型性能對比
此外,我們根據問題計算答案所需的操作數(問題中的某些數值)將測試集(2,312個隨機抽樣的實例)分為不同的等級,并在不同等級的數據上對比模型性能。詳細情況可見圖4。從結果中,我們可以看到,大多數的MWP需要2到4個操作數,而SUMC-Slover在需要更多操作數的數據上表現得比基準模型更好,這表明我們的求解器有潛力解決更復雜的問題。
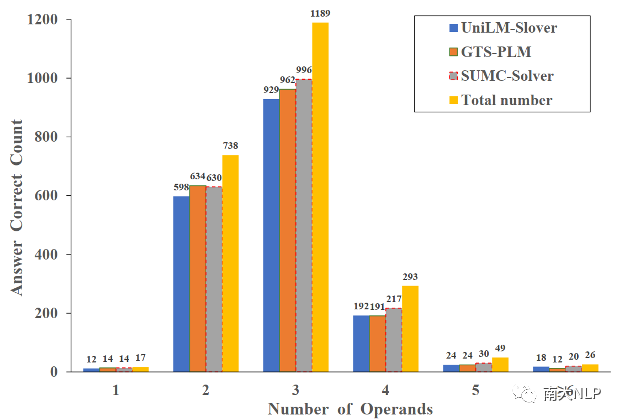
圖4:不同模型在需要不同操作數的測試數據上正確回答問題數量的對比
最后,seq2code框架也可以應用于二叉樹結構,例如可為每個MWP選擇一個二叉樹結構的輸出,并以同樣的方法將其轉換為codes。我們對Math23K的訓練集數據進行了轉換,并對二叉樹codes和M-tree codes進行了比較,結果如下表2所示。可以看出,應用M-tree可以大大減少codes集合的大小,并保證得到的codes能夠覆蓋測試集,這說明M-tree對統一輸出結構的效果非常明顯。
表2:二叉樹與M-tree編碼對比
05
總結
針對數學問題求解的輸出多樣性,我們提出了SUMC-Slover求解器,其應用M-tree來統一多樣化的輸出,以及seq2code模型來學習M-tree。在廣泛使用的MAWPS和Math23K數據集上的實驗結果表明,SUMC-Solver在類似的設置下優于目前一些最先進的方法,并且在低資源場景下有著更好的表現。
審核編輯:劉清
-
編碼器
+關注
關注
45文章
3651瀏覽量
134772 -
PLM
+關注
關注
2文章
123瀏覽量
20877 -
求解器
+關注
關注
0文章
77瀏覽量
4537
原文標題:EMNLP'22 | 基于結構統一M叉編碼樹的數學問題求解器
文章出處:【微信號:zenRRan,微信公眾號:深度學習自然語言處理】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
一種求解關鍵路徑的新算法
基于四叉樹的分形圖像編碼中的剖分決策函數
基于HBase的四叉樹Hilbert索引設計
紅黑樹(Red Black Tree)是一種自平衡的二叉搜索樹




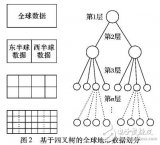
 求一種基于結構統一M叉編碼樹的求解器解決方案
求一種基于結構統一M叉編碼樹的求解器解決方案










評論