大多數(shù)人最先接觸的切線源于圓這種特殊的曲線。因為圓的半徑與所經(jīng)過的切線是垂直的,所以圓的切線很容易被定義:過圓上一點且垂直于該點半徑的那條直線。
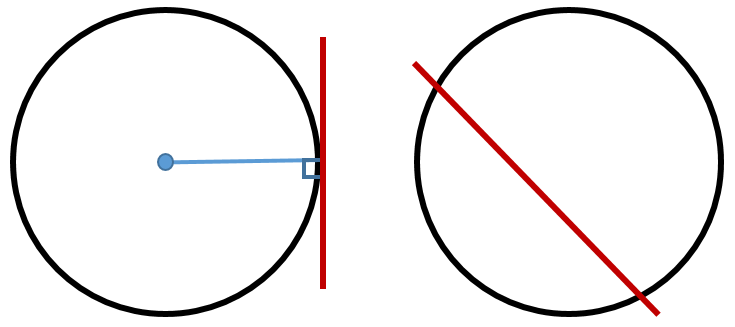
人們發(fā)現(xiàn),圓的割線必定與圓交于兩點,而切線必定只與圓交于一點,因此“只交于一點”這件事成為人們對于切線最深刻的印象。
于是有人根據(jù)這種理解,提出關(guān)于切線的一種定義:
一條與曲線接觸但不切割曲線的直線。
這是切線諸多定義中迄今流傳最廣的那一個。
按此定義,與曲線接觸的情況有兩種,割線為其一,除此之外就是切線了。
何謂割線?割線一詞的英文叫secant,它與section同源,而section的意思很清楚,就是切斷的意思。
如果把割線想象為一把刀,曲線將難逃被分割為多段——至少是分尸兩段的命運!
一旦關(guān)系破裂,切割分分鐘發(fā)生。
于是有了割袍斷義之說。
然后,一切都再也回不去了。
記住:不到那一步,不要輕易切割。
呃,這波語義剖析有點啰嗦得快控制不住了。但我敢保證,正是這種切割所激起的痛感,你此刻腦子里對割線已經(jīng)建立前所未有的深刻認知了。
然而說到“切”,如今現(xiàn)實中,很多時候它只是一個語氣詞。
但正經(jīng)點來說,“切”主要是指下面這種意思。
這樣一來,“切”似乎與“割”或者“切割”沒啥不同?
非也!其實,即使不在討論切線的語境中,“切”的意思也遠非上述這些,它還有“貼近”和“契合”之意,表示剛好靠近,而未越過界限進入對方內(nèi)部。詞語諸如“貼切”、“切中”等皆由此而生。而“切線”一詞,正是取此義而得也。
假設此刻你臉上有一只蚊子,而我又是一位武藝高強手握雙板斧的大咖,我將會用利斧貼著你的臉皮掠過,斧口掠過的路徑就是一條切線,你將毫發(fā)無損,而位于切點的蚊子被準確的砍死。
講了這么久,你現(xiàn)在明白了上面那個切線定義的由來吧!
按照這種切線的定義,考慮如下圖這些情況。
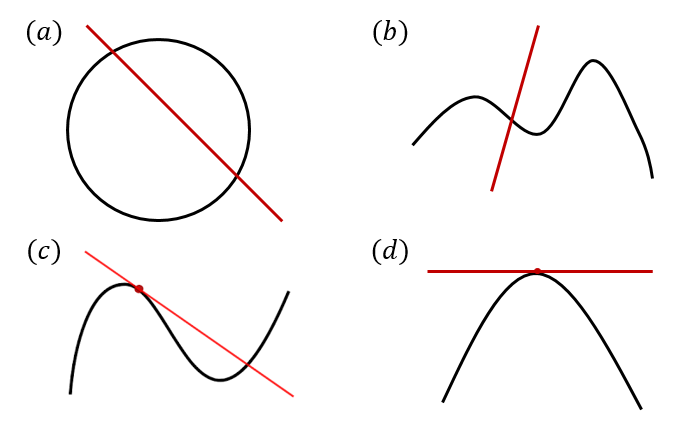
顯然,,和都發(fā)生了切割,所以那些紅線都是割線。而中只是發(fā)生了切,與割不同的是,即使因此而切掉了一點,也可忽略,因為數(shù)學上的點本來就沒大小嘛!因此,曲線沒有因為切線的切而斷掉。
當然,機智如你,有人提出,按此上面這種理解方式,下面這種也是切線,理由是二者有接觸,曲線未被切割。對嗎?
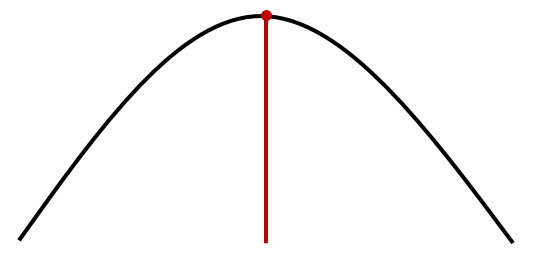
不對不對!切線應該是直線,而你這里是射線嘛。
關(guān)于切線的這樣的一種觀點或約定,一直被廣泛的接受,直到1828年。
因為不斷有人提出:一條切線應該只與曲線上一個點關(guān)聯(lián),而不必管它是否在別的位置切割曲線。按此說法,像上圖中的紅線也應該是切線!
也就是說,對曲線有轉(zhuǎn)向的情況,因為無法避免直線與曲線切割,上面所提到的切線定義無法給出切線。
所以,1828年以后,這種頻繁出現(xiàn)在各種詞典中的定義被正式宣布廢棄了。
如果你還持有這種觀念,那很抱歉,你的觀念已經(jīng)out快兩百年了!
1828年之后,詞典里對切線的給出的定義是:
切線指的是一條剛好觸碰到曲線上某一點的直線。
實際上,“切線”一詞的英文——“tangent”,源自拉丁語“to touch”,表示接觸的意思。竊以為,這種接觸就是點到為止,不過分依靠和攀附。
據(jù)此描述,對于將切線演示出來這件事,具有良好的可操作性:當你拿著一根不太長的直線靠近曲線上的某個確定點時,只要讓你手里的直線與曲線剛好接觸,你手里的直線就是那條要找的切線。
若你將一根剛性直桿搭在一個圓球上,只要你避免桿的兩端與球面直接接觸,可以肯定,桿必定與球保持相切。
如下圖,假設地面光滑,左邊的球與墻壁接觸但無壓力,因此球沒有發(fā)生形變,所以墻面和球面剛好接觸,二者相切。而右邊的球因為受到細線的斜拉力,必定受到墻面的支持力,球面發(fā)生形變,它與墻之間并非點到為止,因此墻面不是球面的切面。
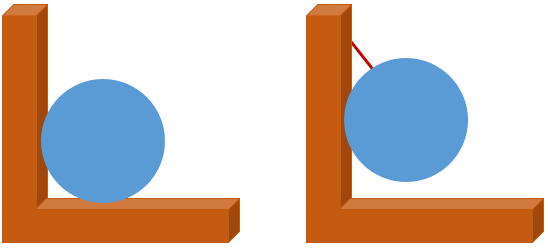
雖然這種切線定義是正確的,并且實際操作性強。但這句話有點模糊,“剛好觸碰”什么意思?感覺正經(jīng)的數(shù)學定義不會這么說,的確不太好理解,所以這個定義的接受度不是很高。
為了解決廣大群眾對數(shù)學知識的向往與有限的理解力之間的矛盾,人們需要一種更淺顯的說法。比如:有幾個交點就算切線?于是,“只交于一點”這么一個最直觀,但卻很容易找到反例的錯誤說法依然占有較大的市場。
難道在漫長的人類文明史中,切線的定義就只是這個?
非也!太小看歷史上的那些聰明的數(shù)學家了!其實早在古希臘時代,人們就給出了準確的定義,后來人們又對切線給出多種定義。但遺憾的是,或許是因為數(shù)學和幾何上的嚴格定義往往是比較抽象的,這些正確定義并未被大眾所熟知。
那么,到底有哪些大牛曾經(jīng)提出過正確的切線的定義呢?其實,古希臘的數(shù)學家歐幾里德和阿基米德、比牛頓稍早的法國數(shù)學家費馬以及牛頓本人等,都對切線做過研究。本文無意去地毯式探求切線定義的發(fā)展歷史,只列舉一下最為重要的兩個定義。
第一個定義來自古希臘三大數(shù)學家之一的阿波羅尼奧斯(Apollonius of Perga,約公元前262~190)。
在數(shù)學中,喇叭角,也稱為horn angle,是一種曲線角,定義為兩條相切的曲線之間形成的角。下面這只牛角表面沿縱向正對的兩條曲線近似牛角尖處相切,因此就形成一個喇叭角。當然,你可能會鉆牛角尖,因為牛角是個立體角。
按照阿波羅尼奧斯的觀點,若切線為直線,那么,切線與曲線之間形成的喇叭角是經(jīng)過該點所有直線與曲線形成的角中最小的那一個。
當然,如果切線沒有被限制為直線,那么在它與所切的曲線之間,可以插入另外的不同曲線,它們之間彼此兩兩相切。例如下圖中,就成功的被插入到和它的切線之間。
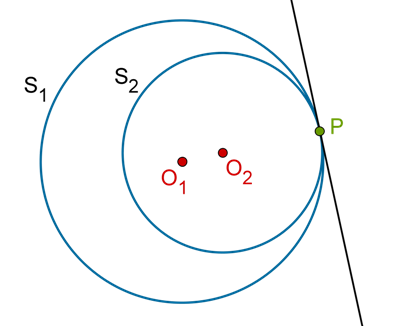
阿波羅尼奧斯將切線定義為一條直線,那么它和曲線之間不可能還能插入其他的直線。話句話說,所謂切線就是那個與曲線接觸并形成最小夾角的直線。
不過,值得注意的是,這種切線的定義只適合于光滑的曲線,如果像下面這種情形,切線是不存在的。圖中紅色的直線只是曲線部分的切線,而非整體的切線。
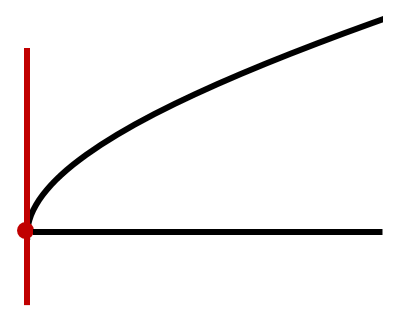
阿波羅尼奧斯不愧為幾何學大師,給出的切線的定義似乎無懈可擊。即使將切線推廣至曲線,也是可以的。因為若切線是形狀大小固定曲線,當你試圖將另一條同樣的曲線插入喇叭角,并使它同一位置與切點重合時,它必然與原來的切線重合。換句話說,切線和曲線之間也無法再插入一條(同樣的)切線了。
但事實上,將切線限定為直線也是合理的。
這樣做,并不妨礙研究兩個曲線相切這件事。因為曲線是否相切可以根據(jù)它們在某個公共點上是否共有切線來判定。事實上,我們就是這么做的!不光如此,人們還規(guī)定,當兩個曲線在一個公共點的切線互相垂直時,我們就說這兩個曲線正交。
設圓與一曲線相切,若圓在曲線的凹的一側(cè),且曲線在切點處的曲率半徑等于圓半徑,則該圓稱作曲線的密切圓,如下圖所示。
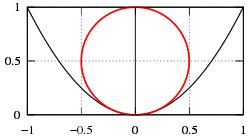
密切圓有個與切線類似的性質(zhì),在它與曲線之間,不存在其他與曲線相切的圓。這就是為什么稱其為密切的原因。好比一對伴侶,情之密切,絕不容外人介入。
一些特殊的曲線的密切圓會形成美妙的圖案,典型的案例是阿基米德螺線。阿基米德螺線,也稱等速螺線,是一個點勻速離開一個固定點的同時又以固定的角速度繞該固定點轉(zhuǎn)動而產(chǎn)生的軌跡。在極坐標系中,這種曲線可表示為
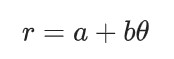
下圖這個看起來像蚊香盤的東東就是這種曲線。

沿著等速螺線從內(nèi)到外,畫出半徑逐漸增大的密切圓,形成如下奇特的圖案(點擊看大圖)。可以看出,這本身提供了一種畫等速螺線的辦法,因為相鄰的圓的切點移動的軌跡正好就是螺線本身。
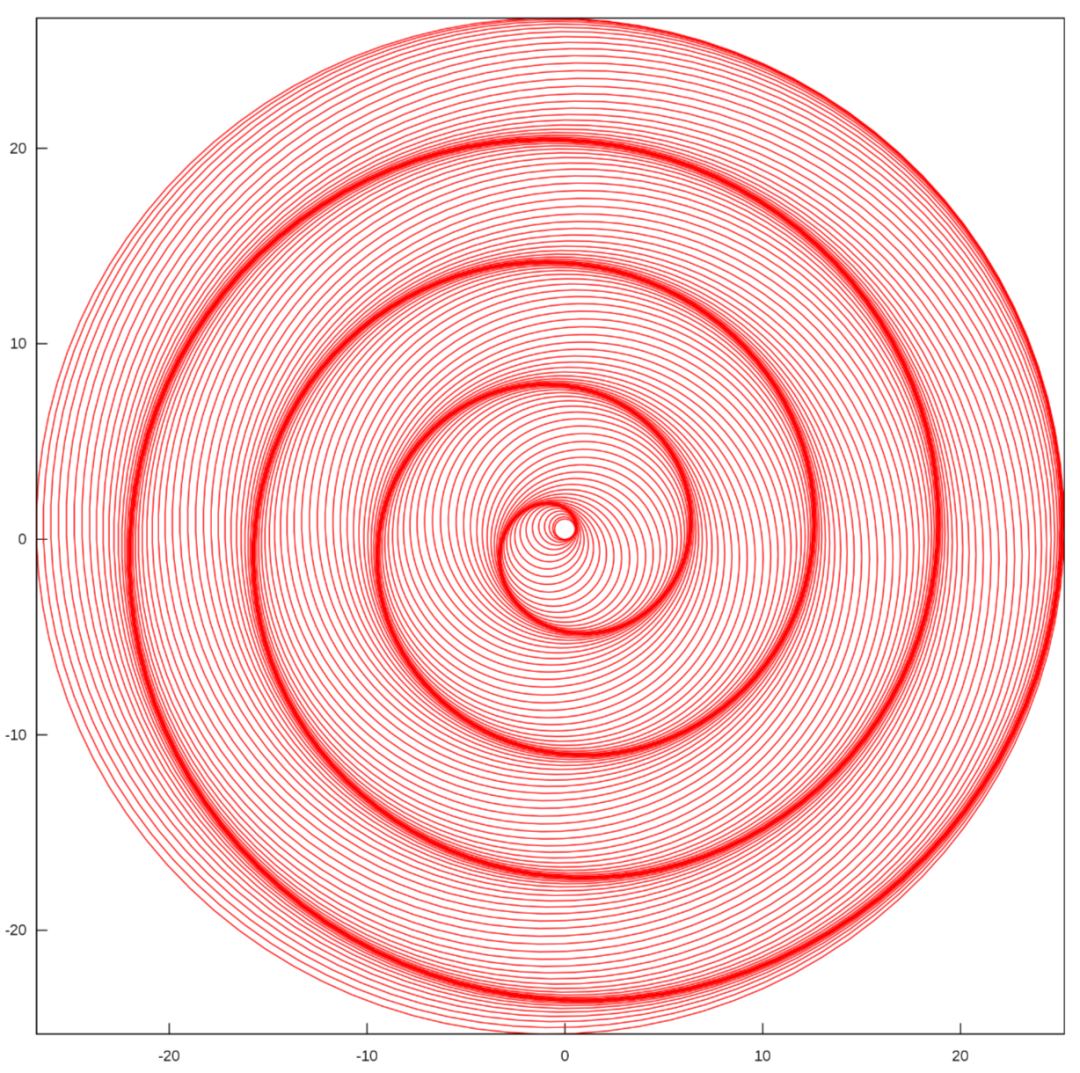
再發(fā)個動圖娛樂一下吧。

關(guān)于阿波羅尼奧斯給出的切線定義就介紹這么多吧。
第二個切線定義,也是現(xiàn)代被廣泛接受的切線定義,源于德國偉大的數(shù)學家戈特弗里德·威廉·萊布尼茲(Gottfried Wilhelm Leibniz,1646-1716)。
他給出的定義非常簡單:切線就是曲線上的割線在兩個交點無限接近時所對應的那條直線。
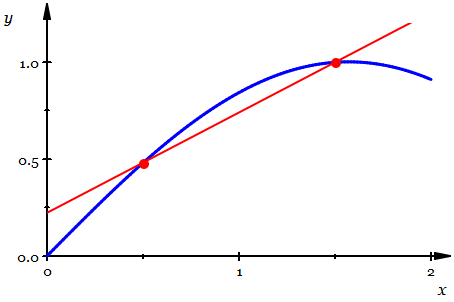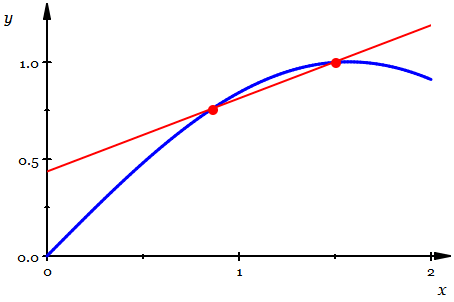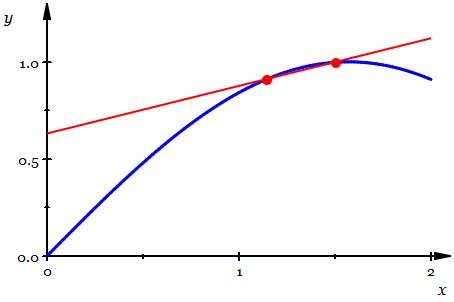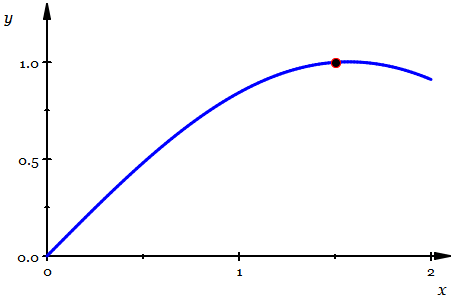
如上圖所示,紅色線是一條割線,它與曲線交于兩點。讓其中一個交點固定不動,而讓另一個交點沿著曲線不斷靠近那個不動點,在這個過程中,割線不斷旋轉(zhuǎn)。
當二者之間的距離無限靠近時,它們決定的那條割線不再動了,這就形成了一條特殊的割線——哦,此時不再是割線了,而是一條被定義為“切線”的直線。
所以,切線是什么?切線就是割線的交點無限靠近時的極限。它的斜率可以通過極限運算確定,即

根據(jù)這個定義,只要知道曲線的函數(shù)表達式,就可以通過求導的方法得到曲線在任一點的切線的斜率,加上這個已知點,我們就能唯一的將切線確定下來。
當然,對于非光滑的曲線,由于在某些位置,導數(shù)是不存在的,因此切線也就不存在了。
萊布尼茲關(guān)于切線的定義里,蘊含了他的微分思想。
學過微分的都知道,微分是無限趨近于零,但卻不等于零的值。這保證了兩個點還是兩個點,只是彼此無限靠近!這一點非常重要。
因此,切線是曲線上無限接近,但又沒有完全重合的兩點決定的一條直線。
這個定義與大多數(shù)人心目種的切線定義不同,很多人往往認為切點是一個點,其實你想想,一個點怎么能確定一條直線呢?必須要兩個點啊!
所以,切點從本質(zhì)上講包含兩個點,兩個無限靠近的點。
呃,是不是有點被顛覆世界觀的的感覺?切點不就是一個點嘛,怎么會是兩個點?
是的,如果你只是關(guān)心位置,那么切點就是一個點,它就是那個不動的點蛻變而來的。但只是在那個動點無限靠近時,它才轉(zhuǎn)正成為切點!在此之前,它不是切點。
所以,萊布尼茲的定義是多么美妙!
而萊布尼茲的定義與阿波羅尼奧斯的定義是一致的,下面動畫清楚的顯示這一點:你無法在切線與曲線形成的角里再插入一條直線。
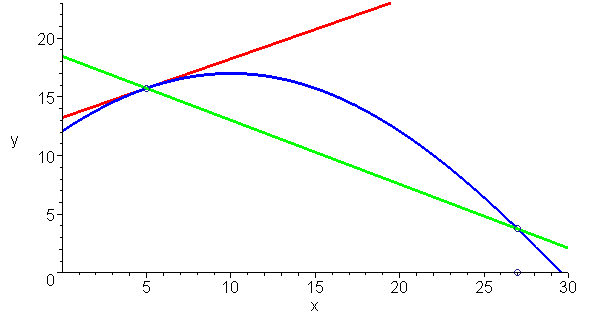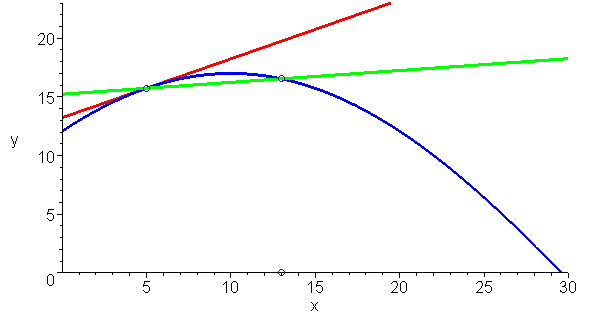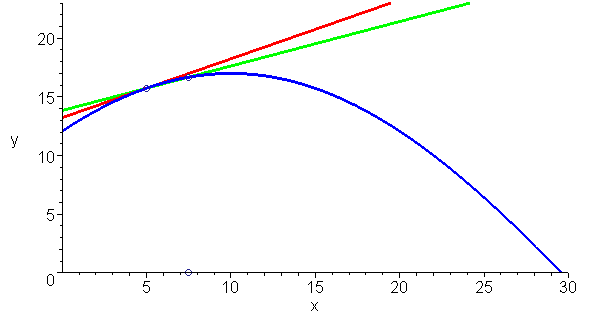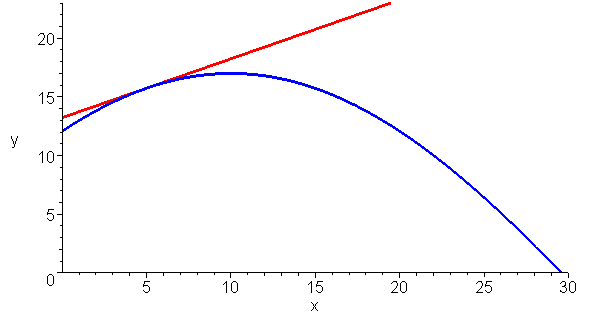
最后再來看一個問題:曲線上任一點是否只有一條切線呢?
很多人的答案是肯定的,并且在學習電場時,還據(jù)此來理解電場線為什么不能相交的問題。但恐怕很多人在這個問題上有點邏輯顛倒。實際上,電場線不能相交,那是因為任一點場矢量的方向是唯一確定的,并不能說明曲線上每點只能有一條切線!
實際上,過一點有多條切線的情況是存在的!
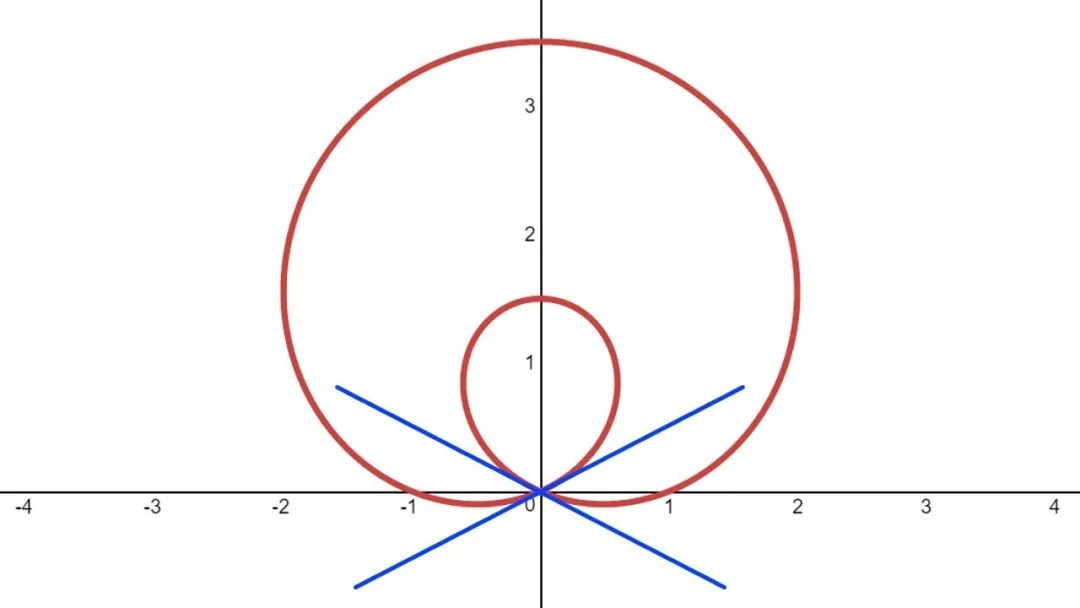
比如下面這種被稱Pascal或lima?on的曲線,在原點處就有兩條切線。這是一種奇點的特殊情況,這種情況下,前面的定義失效了。但可以根據(jù)純代數(shù)方法找到這些奇點的切線方程,這里就不涉及了。
與曲線的切線類似,與給定點處的曲面相切的平面是“剛好接觸”該點處曲面的平面。例如,下圖中,球面與平面剛好接觸,平面是球面的切面。

現(xiàn)在,切線的概念已經(jīng)被推廣,成為微分幾何中最基本的概念之一。
審核編輯:劉清
-
切線模量
+關(guān)注
關(guān)注
0文章
3瀏覽量
8681
原文標題:切與割有什么區(qū)別?到底什么是切線?切點真的是一個點嗎?
文章出處:【微信號:bdtdsj,微信公眾號:中科院半導體所】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
同時DSP2812的源文件,命名不同,到底有什么區(qū)別?
hdmi與vga有什么區(qū)別
CAN通訊中摩托羅拉格式與英特爾格式到底有什么區(qū)別
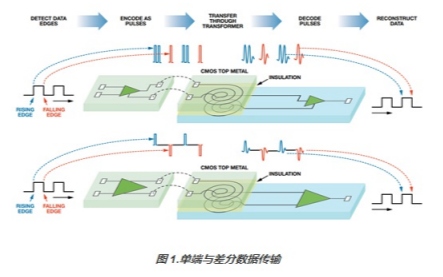
單端與差異數(shù)據(jù)傳輸到底有什么區(qū)別




 切與割有什么區(qū)別?到底什么是切線?
切與割有什么區(qū)別?到底什么是切線?










評論