看了很多講交叉熵的文章,感覺都是拾人牙慧,又不得要領。還是分享一下自己的理解,如果看完這篇文章你還不懂這倆概念就來掐死我吧。
1
『先翻譯翻譯,什么叫驚喜』
我們用 表示事件 發(fā)生的概率。這里我們先不討論概率的內(nèi)涵, 只需要遵循直覺: 可以衡量事件 發(fā)生時會造成的驚喜(行文需要,請按照中性理解)程度: 概率越低的事件發(fā)生所造成的驚喜程度高;概率越高的事件發(fā)生所造成的驚喜程度低。 但是概率倒數(shù)這一運算的性質(zhì)不是很好,所以在不改變單調(diào)性的情況下,可以將驚喜度(surprisal)定義為:
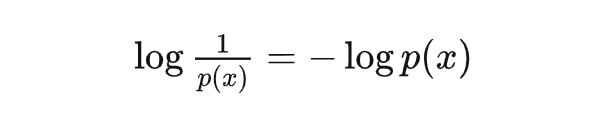
這樣定義后產(chǎn)生了另外兩個好處: 1. 確定性事件的驚喜度 = 0; 2. 如果有多個獨立事件同時發(fā)生,他們產(chǎn)生的驚喜度可以直接相加。是的,一個事件發(fā)生概率的倒數(shù)再取對數(shù)就是驚喜。
2
『信息熵,不過只是驚喜的期望』
驚喜度,在大部分文章里,都叫做信息量,但這個命名只是香農(nóng)根據(jù)他研究對象的需要而做的,對于很多其它的場景,要生搬硬套就會變得非常不好理解了。 信息量 = 驚喜度,那么信息熵呢?看看公式不言自明:
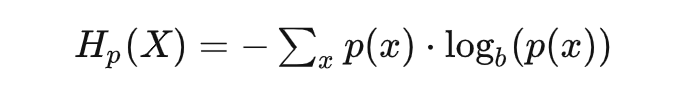
或是連續(xù)形式:
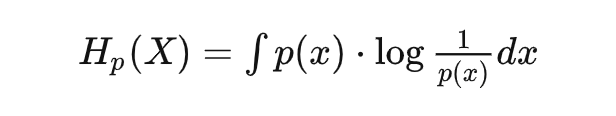
這不就是驚喜度的期望嗎? 換句話說,信息熵描述的是整個事件空間會產(chǎn)生的平均驚喜。 什么情況下,平均驚喜最低呢?確定事件。以某個離散隨機分布為例,整個分布在特定值 為 1,其它處均為 0,此時的信息熵/平均驚喜也為 0。 什么情況下產(chǎn)生的平均驚喜最高呢?自然是不確定越高平均驚喜越高。對于給定均值和方差的連續(xù)分布,正態(tài)分布(高斯分布)具有最大的信息熵(也就是平均驚喜)。所以再想想為什么大量生活中會看到的隨機事件分布都服從正態(tài)分布呢?說明大自然有著創(chuàng)造最大驚喜的傾向,或者說,就是要讓你猜不透。這也是理解熱力學中的熵增定律的另一個角度。
3
『交叉熵,交叉的是古典和貝葉斯學派』
對于概率,比較經(jīng)典的理解是看做是重復試驗無限次后事件頻率會逼近的值,是一個客觀存在的值;但是貝葉斯學派提出了另一種理解方式:即將概率理解為我們主觀上對事件發(fā)生的確信程度。針對同一個隨機變量空間有兩個分布,分別記作和; 是我們主觀認為會發(fā)生的概率,下標代表 subjective; 是客觀上會發(fā)生的概率,下標 ○ 代表 objective。 這種情況下,客觀上這個隨機事件會給我們造成驚喜的期望應該是:
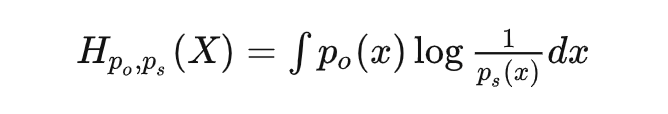
這個量 is a.k.a 交叉熵。 再翻譯一下,交叉熵是什么?可以理解為:我們帶著某個主觀認知去接觸某個客觀隨機現(xiàn)象的時候,會產(chǎn)生的平均驚喜度。 那什么時候交叉熵(也就是我們會獲得的平均驚喜度)會大?就是當我們主觀上認為一個事情發(fā)生的概率很低很大),但是客觀上發(fā)生概率很高很大) 的時候,也就是主觀認知和客觀現(xiàn)實非常不匹配的時候。機器學習當中為啥用交叉熵來當作損失函數(shù)應該也就不言自明了。
4
『相對熵,K-L散度』
交叉熵可以衡量我們基于某種主觀認識去感受客觀世界時,會產(chǎn)生的平均驚喜。但是根據(jù)上面的分析,即使主觀和客觀完全匹配,這時交叉熵等于信息熵,只要事件仍然隨機而非確定,就一定會給我們造成一定程度的驚喜。那我們要怎么度量主觀認識和客觀之間差異呢?可以用應該用以當前對“世界觀”產(chǎn)生的驚喜期望和完全正確認識事件時產(chǎn)生的驚喜期望的差值來衡量,這個就是相對熵(常稱作 KL-散度),通常寫作:
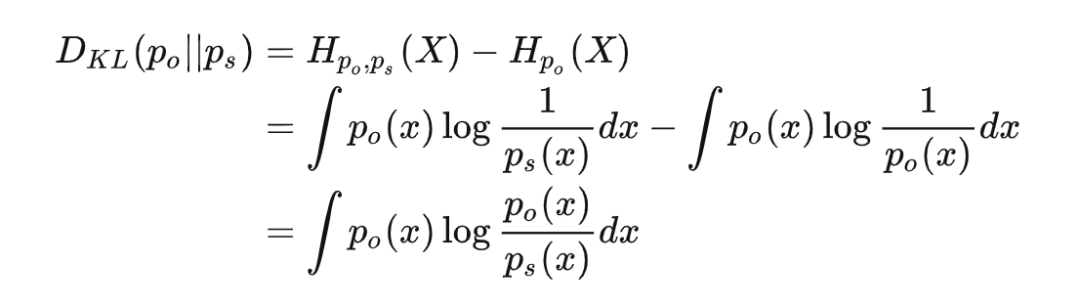
當我們的主觀認知完全匹配客觀現(xiàn)實的時候,KL-散度應該等于 0,其它任何時候都會大于 0。由于存在恒為正這一性質(zhì),KL-散度經(jīng)常用于描述兩個分布是否接近,也就是作為兩個分布之間“距離”的度量;不過由于運算不滿足交換律,所以又不能完全等同于“距離”來理解。 機器學習中通常用交叉熵作為損失函數(shù)的原因在與,客觀分布并不隨參數(shù)變化,所以即使是優(yōu)化 KL-散度,對參數(shù)求導的時候也只有交叉熵的導數(shù)了。
審核編輯 :李倩
-
機器學習
+關注
關注
66文章
8408瀏覽量
132572 -
交叉熵
+關注
關注
0文章
4瀏覽量
2361
原文標題:一篇文章講清楚交叉熵和KL散度
文章出處:【微信號:zenRRan,微信公眾號:深度學習自然語言處理】歡迎添加關注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關推薦
晶臺DIP6 零交叉可控硅光耦KL304X,峰值擊穿電壓400V,符合ROHS、REACH和無鹵要求

電容的“通交流、阻直流”,終于有人講清楚了!
可控硅驅(qū)動光電耦合器KL308X 產(chǎn)品規(guī)格書
可控硅驅(qū)動光電耦合器KL306X 產(chǎn)品規(guī)格書
可控硅驅(qū)動光電耦合器KL303X 產(chǎn)品規(guī)格書
高速光耦KL2601&KL2611 產(chǎn)品規(guī)格書
高速光耦KL220X 產(chǎn)品規(guī)格書
KL4N29~33 達林頓光耦 產(chǎn)品規(guī)格書
阿里云設備的物模型數(shù)據(jù)里面始終沒有值是為什么?
M8連接器對使用環(huán)境有什么要求,一篇文章講清楚!

干貨!收藏!一文講清楚數(shù)據(jù)治理到底是什么?
工業(yè)級連接器如何做到高抗沖擊性?選款一定要了解這幾點





 一篇文章講清楚交叉熵和KL散度
一篇文章講清楚交叉熵和KL散度












評論