本文來源電子發燒友社區,作者:jf_55236000, 帖子地址:https://bbs.elecfans.com/jishu_2292914 _1_1.html
作為一款應用于實時控制的DSP芯片,其運算性能起著決定性作用,下面就來評估一下DSC28034的運算性能,
評估環境:
硬件平臺:Start_DSC28034湖人開發板
芯片主頻:120MHz
測試算法:IQmath
評估方法:
配置一個CPU定時器,計數器每個時鐘周期減1,在執行算法前先記錄當前定時器計數器值Cnt1,算法執行完成后再次記錄當前定時器計數器Cnt2,則算法執行時間為Cnt2- Cnt1個時鐘周期,換算成以ns為單位的標準時間則為:(Cnt2- Cnt1)÷120×1000ns,
定時器的配置如下:
//==========CPU Timer 1=========================//
CpuTimer1Regs.PRD.all = 120000000; // Initialize timer period to 1s:
CpuTimer1Regs.TPR.bit.PSC = 0; // Initialize pre-scale counter to divide by 1 (SYSCLKOUT):
CpuTimer1Regs.TPR.bit.TDDR = 0;
CpuTimer1Regs.TCR.bit.TSS = 1; // Make sure timer is stopped:
CpuTimer1Regs.TCR.bit.TRB = 1; // Reload all counter register with period value:
CpuTimer1Regs.TCR.bit.TIE = 0; // 0 = Disable/ 1 = Enable Timer Interrupt
CpuTimer1Regs.TCR.bit.TSS = 0; // Start CpuTimer1
先貼上測試結果:
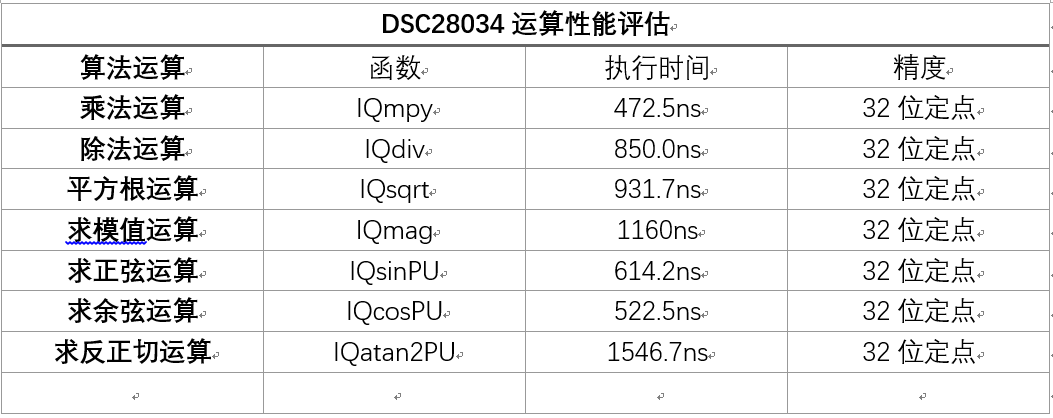
這個運算性能算很不錯的了,比一般ARM的M3或者M4強很多了,可以滿足一般的實時控制需求,但比起TI的一些帶FPU的DSP還是要差很多,比如TI的28069,算一個單精度浮點乘法只要一個流水線周期,大概80多個ns,
具體算法性能評估情況如下:
32位定點乘法運算IQmpy:
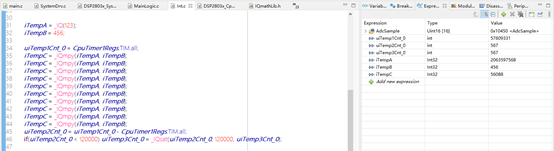
計算結果:IQmpy(a,b) = a*b>>Q,即((123<<24)*456)>>24 = 123*456 = 56088,
計算時間:567÷120÷10 ×1000 = 472.5ns
32位定點除法運算IQdiv:
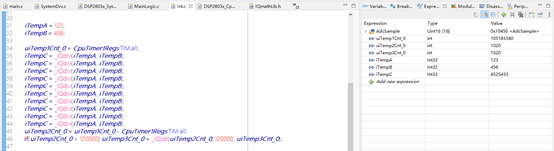
計算結果:IQdiv(a,b) = (a<,
)>
計算時間:1020÷120÷10 ×1000 = 850ns
32位定點平方根運算IQsqrt:
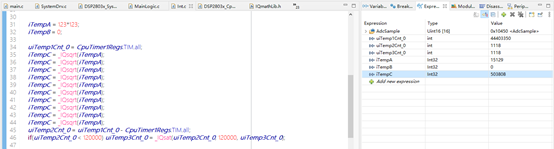
計算結果:IQsqrt(a) = sqrt (a<),即sqrt(123*123<<24)>
計算時間:1118÷120÷10 ×1000 = 931.7ns
32位定點求模值運算IQmag:
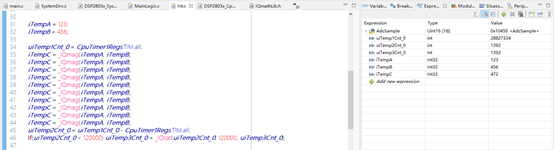
計算結果:IQmag(a,b) = sqrt (a*a+b*b),即 sqrt (123*123+456*456) = 472
計算時間:1392÷120÷10 ×1000 = 1160ns
32位定點求正弦運算IQsinPU:
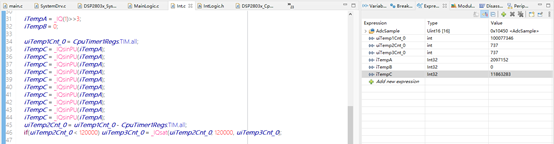
計算結果:IQsinPU(a) = sin (a)<<24,即
sin (360°>>3) = sin(45°)<<24 = 11863283
計算時間:737÷120÷10 ×1000 = 614.2ns
32位定點求余弦運算IQcosPU:
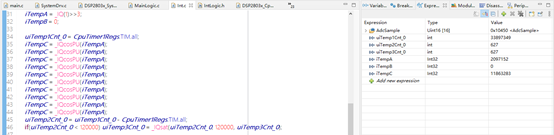
計算結果:IQcosPU(a) = cos (a)<<24,即
cos (360°>>3) = cos(45°)<<24 = 11863283
計算時間:627÷120÷10 ×1000 = 522.5ns
32位定點求反正切運算IQatan2PU:
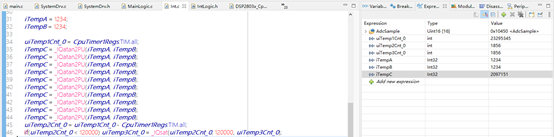
計算結果:IQtan2PU(a,b) = 點(a,b)與x軸夾角/360°<<24,即
45/360<<24 = 2097151
計算時間:1856÷120÷10 ×1000 = 1546.7ns
-
中科昊芯
+關注
關注
5文章
80瀏覽量
5184 -
開發板試用
+關注
關注
3文章
301瀏覽量
2109
發布評論請先 登錄
相關推薦
有獎丨米爾 全志T536開發板免費試用

瑞芯微主板/開發板Linux系統播放音頻方法,觸覺智能RK3562開發板演示

追加名額丨米爾瑞芯微RK3576開發板有獎試用

有獎丨米爾 瑞芯微RK3576開發板免費試用

設計用于TMS320C203評估的TMS320C203 DSP開發板

中科昊芯攜基于自研RISC-V DSP芯片的無人機解決方案完美收官2024慕尼黑華南電子展

喜報!中科昊芯榮獲國家級專精特新“小巨人”企業稱號

點擊參與米爾NXP i.MX 93開發板有獎試用





 【中科昊芯Start_DSC28034PNT湖人開發板試用體驗】DSP運算性能評估
【中科昊芯Start_DSC28034PNT湖人開發板試用體驗】DSP運算性能評估












評論