01、導讀

鋰硫（Li-S）電池理論能量密度高、成本低，是最有前途的儲能系統之一。然而，放電期間從Li2S4到Li2S的緩慢還原動力學阻礙了Li-S電池的實際應用。盡管已經提出了各種電催化劑來改善反應動力學，但由于硫還原反應（SRR）的復雜性，其電催化機理尚不清楚。因此，深入了解電催化機理對于設計先進的電催化劑至關重要。

02、成果背景

近日，Angewandte Chemie International Edition上發表了一篇題為“An Electrocatalytic Model of the Sulfur Reduction Reaction in Lithium–Sulfur Batteries”的文章，該文章以雜原子摻雜碳材料為例，基于系統密度泛函理論計算，建立了鋰硫電池中SRR的電催化模型，揭示了SRR的化學機制。LiSy?(y=1,2或3)自由基的吸附能被用作預測反應路徑、速率決定步驟和過電位的關鍵描述符。該研究為探索復雜的SRR機制和設計高性能鋰硫電池電催化劑提供了一個的理論模型。

03、關鍵創新

（1）本工作建立了一個電催化模型，用于探索SRR（Li2S4→ Li2S）；

（2）通過LiSy?自由基（y=1、2或3）吸附過程中的吉布斯自由能變化（ΔGradical），可以確定SRR在工作電位下的速率決定步驟和能壘；

（3）最后，建立了η與ΔGradical值的關系圖，以指導先進SRR電催化劑的設計。

04、核心內容解讀

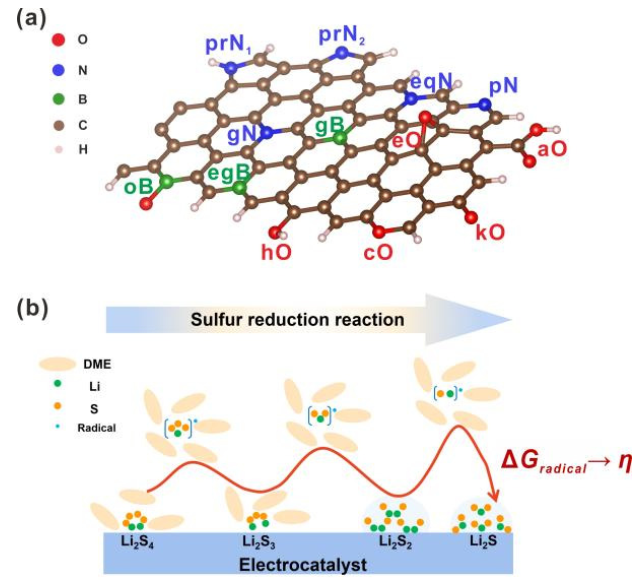
圖1.（a）雜原子摻雜石墨烯納米帶（X=O，N，B）和（B）鋰硫電池第二放電平臺的反應機理示意圖。@Wiley

雜原子摻雜GNR（X摻雜GNR）因其優異的導電性和在鋰硫電池中具有良好的電催化活性而被選為本工作中的電催化劑模型。通過將三種非金屬元素（X=N、O和B）取代邊緣或體相碳原子引入石墨烯基體，構建了一系列周期性GNR模型。考慮了13種摻雜劑（圖1a），包括酮基（kO）、羧基（aO）、羥基（hO）、環氧基（eO）、環氧（cO）、石墨氮（gN）、吡啶氮（pN）、C–N–C型氮（eqN）、吡咯烷氮（prN1）、無氫吡咯烷（prN2）、石墨硼（gB）、B–2C–O型硼（oB）和C–B–C型硼（egB）。

由于SRR（圖1b）是六電子還原反應（Li2S4+6Li++6e?→4Li2S），整個轉化過程分為六個基本步驟，生成一系列LiSy?自由基和Li2Sy分子。考慮到不同的溶解度，可溶性Li2S4、Li2S3和LiSy?自由基在DFT計算中被視為分子，而不溶性Li2S和Li2S2被視為晶體。

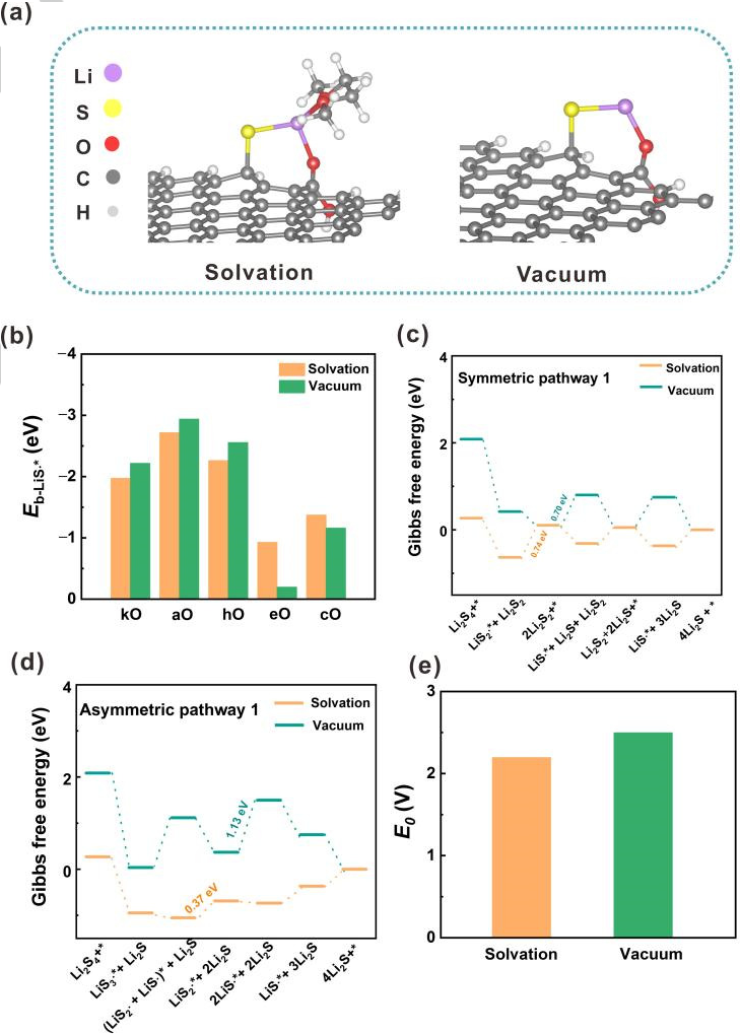
圖2.溶劑化和真空模型之間的比較。（a）LiS?自由基的吸附構型，左：溶劑化模型；右：真空模型。（b）LiS?自由基在氧摻雜GNR上的吸附能（Eb）。在（c）對稱和（d）不對稱路徑中，U=2.15 V（vs.Li/Li+）時的自由能圖。（e）鋰硫電池第二平臺的計算平衡電位。@Wiley

由于溶劑化效應在調節溶液中分子結構和反應行為中具有重要作用。因此，采用溶劑化模型與真空模型進行比較（圖2a）。具體地，使一個或兩個1，2-二甲氧基乙烷（DME）分子分別與可溶性LixSy（x＝1或2；y＝1、2、3或4）自由基和分子相互作用。真空模型和溶劑化模型在含硫物質的吸附能、SRR過程的速率決定步驟和鋰硫電池第二放電平臺的計算平衡電位（E0）方面表現出巨大差異。

首先，比較溶劑化和真空模型下的LiSy?自由基吸附能，以O摻雜GNR為例（圖2b）。盡管在兩種模型中，LiSy?自由基在O摻雜GNR上的吸附強度呈現出相同的趨勢，但溶劑化效應可以減弱或增強吸附。一般而言，在溶劑化模型中，摻雜kO、aO和hO的GNRs對LiS?自由基的吸附能比在真空模型中要小約0.25 eV，而eO摻雜的GNR的吸附能增加0.73eV。在摻雜O的GNRs上，LiS2?和LiS3?自由基也觀察到類似的現象。。

其次，溶劑化效應可以調節SRR過程中的速率決定步驟。速率決定步驟被定義為在平衡電位下ΔG最大的步驟。以O摻雜GNR的SRR為例（圖2c、d），第二步是溶劑化模型中aO和hO摻雜GNRs的速率決定步驟。然而，在真空模型中第三步成為速率決定步驟。

第三，這兩個模型表現出非常不同的第二平臺E0。溶劑化模型的E0（2.19 V）與實驗恒流間歇滴定技術的結果（2.10 V～2.20 V）極為相似。相反，真空模型的誤差為0.34 V（圖2e）。上述結果表明，溶劑化效應在探究SRR機理中發揮了極其重要的作用，因此將溶劑化模型用于進一步的計算。

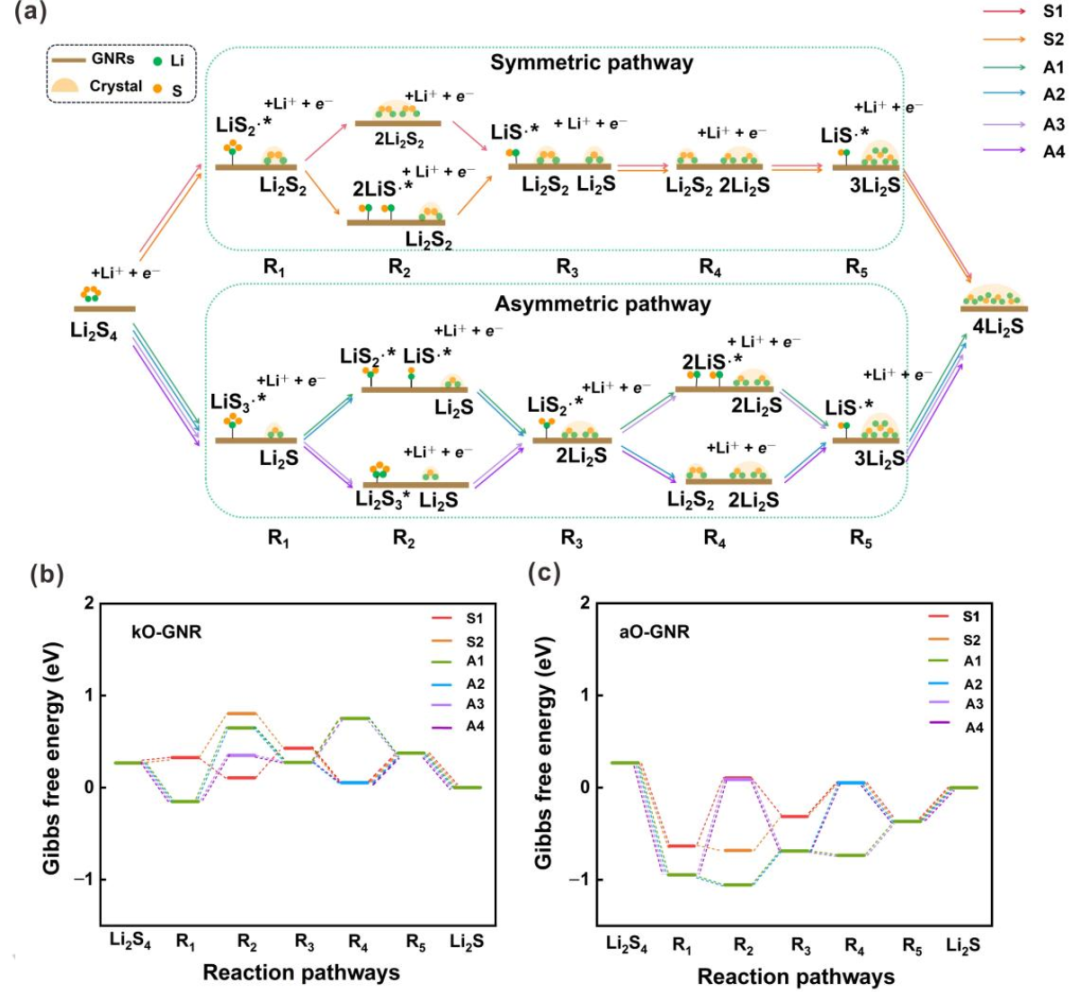
圖3.SRR過程反應機理的探索。（a）所有可能反應途徑的示意圖。（c）摻雜kO的GNR和（d）摻雜aO的GNG上六種可能路徑在U＝2.15 V（vs.Li/Li+）下的自由能圖。S1–S2、A1–A4和R1–R5分別代表SRR過程中的對稱路徑、不對稱路徑和反應中間體。@Wiley

通常，根據Li2S4分解機理，SRR反應可主要分為兩類，即對稱路徑和不對稱路徑。然而，一些中間態總是比它們的最終產物具有更高的能量。例如，不對稱路徑中R1有兩種可能的狀態，即LiS3?*+Li2S和LiS?*+Li2S3（*表示該物質吸附在電催化劑上）。對于所有GNR，上一個總是比下一個更穩定。因此，在排除不可能的路徑后，可以大大簡化整個反應路徑（圖3a）。在簡化的機制中，Li2S4被還原為LiS2?自由基和Li2S2，最后是對稱路徑中的Li2S。然而，Li2S4被還原為LiS3?自由基和Li2S，最后是不對稱路徑中的Li2S。因此，SRR路徑可以進一步細分為兩個對稱路徑（S1和S2）和四個不對稱路徑（A1–A4）。

在對稱路徑中，LiS2?*首先由吸附在表面上的Li2S4產生。然而，LiS2?*分別在對稱路徑S1和對稱路徑S2中的第二步轉化為Li2S2固體或兩種LiS?*。在第三和第五步中，Li2S2固體可以進一步還原并產生吸附自由基LiS?*和Li2S固體。LiS?*隨后在第四和第六步中轉化為Li2S固體。隨后的四個步驟對于S1和S2路徑是相同的。因此，每一步的自由能變化（ΔGi）由等式（1）計算：

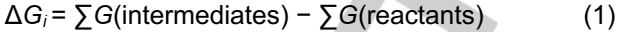
其中∑G（中間體）和∑G（反應物）分別表示每個中間體和反應物的吉布斯能之和。基于每個ΔGi的值，可以通過U=2.15 V（vs.Li/Li+）下的能量分布來探索SRR的反應機理（圖3b、c）。對稱路徑S1在第二和第五步的能量變化比路徑S2低。因此，在對稱分解機制中，路徑S1是優選的。

與對稱機制相比，包括四種不同分解路徑的不對稱機制要復雜得多，涉及更多中間體（圖3a）。吸附的LiS3?*自由基在所有四種路徑的第一步形成，但可以在以下步驟中進一步轉化為不同的中間體。在不對稱路徑A1和A2中，LiS3?*在第二步分解成LiS2?*和LiS?*自由基，LiS?*自由基隨后轉化為Li2S固體。而在不對稱路徑A3和A4中，第二步是形成Li2S3中間體，并進一步產生吸附的LiS2?*自由基。在第四步時，LiS2?*進一步分裂為兩個LiS?*自由基，LiS?*自由基在不對稱路徑A1和A3中再次轉化為Li2S固體。然而，在不對稱路徑A2和A4中，LiS2?*在第四步中進一步還原為Li2S2固體，并生成LiS?*。最后，LiS?*在第六步中轉化為Li2S固體。根據能量分布（圖3b、c），不對稱路徑A1在第三、第四、第五和第六步的能量變化低于其他不對稱路徑A2–A4。因此，在不對稱分解機制中，途徑A1是優選的。

根據U=2.15 V (vs. Li/Li+)時的能壘進一步考慮對稱路徑S1和非對稱路徑A1之間的競爭關系。aO、hO、pN、eqN、oB和egB摻雜的GNR更傾向于不對稱途徑A1，這表明在這六個X摻雜GNR上優先產生LiS3?*。相反，其他7個摻雜X的GNRs產生固體Li2S2的主要路徑是對稱路徑。

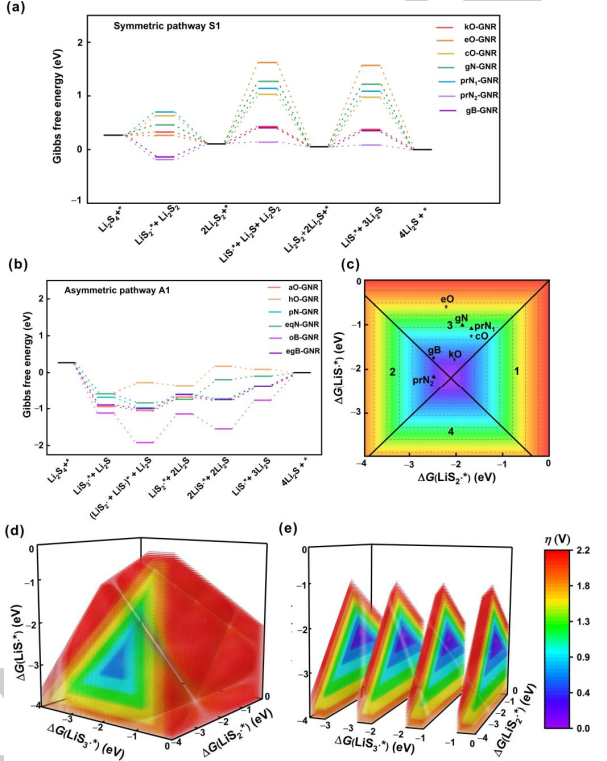
圖4.SRR的電催化模型。遵循（a）對稱路徑1和（b）不對稱路徑1的X摻雜GNR在U=2.15 V（vs.Li/Li+）下的自由能圖。將過電位與自由基在經歷（c）對稱路徑和（d）不對稱路徑GNR上的吸附吉布斯自由能聯系起來的區域圖。（e）圖d的切片圖。@Wiley

圖4a、b給出了在2.15 V vs. Li/Li+條件下最有利反應機理的自由能分布，用以比較不同雜原子摻雜的GNRs催化活性。第一步，吉布斯自由能隨著電勢的增加而上升，被視為SRR過程中的速率決定步驟。對稱路徑為不同電催化劑提供了不同的速率決定步驟（圖4a）。具體而言，Li2S2固體轉化為LiS?*, 步驟3或步驟5是分別具有0.32、1.52、0.92、1.16、1.03和0.30 eV能壘的kO、eO、cO、gN、prN1和gB摻雜GNR的速率決定步驟。Li2S2形成的第二步是prN2摻雜的GNR速率決定步驟，能壘為0.30 eV。 進一步構建區域圖，以提供探測SRR機制的原則（圖4c–4e）。LiS3?、LiS2?和LiS?自由基在電催化劑上的吸附吉布斯自由能分別為ΔG(LiS3?*)、ΔG(LiS2?*)和ΔG(LiS?*)。η和相應的速率決定步驟可從這三個描述符中得出。在對稱路徑中，η值由ΔG(LiS2?*)和ΔG(LiS?*)決定。得到的二維(2D)圖呈金字塔形狀，可分為四個區域，代表四個不同的速率決定步驟(圖4c)。具體來說，當ΔG(LiS2?*)和ΔG(LiS?*)在區域1或2相交時，η與ΔG(LiS2?*)呈現火山圖關系。當ΔG(LiS2?*)比?2.23 eV更正時，步驟1是電位限制步驟，而ΔG(LiS2?*)比?2.23 eV更負時，步驟2是電位限制步驟。同樣，當ΔG(LiS2?*)和ΔG(LiS?*)在區域3或區域4相交時，催化活性可以用η與ΔG(LiS?*)相關聯的火山圖來描述。當ΔG(LiS?*)比?2.18 eV更正時，電位受到步驟3的限制。當ΔG(LiS?*)比?2.18 eV更負時，步驟4為電位限制步驟。二維圖中的連接點對應兩個火山頂部η=0 V的點，ΔG(LiS2?*)和ΔG(LiS?*)分別等于?2.23和?2.18 eV。如圖4c所示，prN2和gB摻雜的GNR在對稱路徑中的其他GNR中表現出最低的過電位（0.34 V），這得益于LiS2?(摻prN2和gB的GNR分別為?1.22和?1.17 eV)和LiS?(摻prN2和gB的GNR分別為?2.41和?1.99 eV)良好的折中。 在非對稱機制中，圖被繪制為ΔG(LiS3?*)、ΔG(LiS2?*)和ΔG(LiS?*)的函數，表示為一個三維(3D)圖(圖4d)。類似地，給定催化劑的活性可以直接從3D圖中獲得。具體地說，速率決定步驟和η可以通過固定不同的描述符來實現。3D圖被分割成幾個2D圖，整合了其他兩個描述符（ΔG(LiS2?*)和ΔG(LiS?*))（圖4e）。通過2D圖中心部分的尺寸和顏色得到速率決定步驟和η，這取決于固定的ΔG(LiS3?*)。 對于摻雜了hO和eqN的GNRs，決定速率步驟是LiS2?*分解為LiS?*，最大η分別為0.58和0.61 V。對于aO、pN、oB和egB摻雜的GNRs，決定速率步驟是Li2S2分解為LiS?，最大η值分別為0.41、0.42、0.82和0.43 V。最大η由三個描述符控制(ΔG(LiS3?*)、ΔG(LiS2?*)和ΔG(LiS?*))。結果表明，在不對稱機制下，最佳的電催化劑應具有理想的吸附吉布斯自由能平衡，對于ΔG(LiS3?*)、ΔG(LiS2?*)和ΔG(LiS?*)分別為?2.20、?2.25和?2.15 eV，從而產生較小的過電位。

05、成果啟示

本工作通過DFT計算系統地研究了鋰硫電池中的SRR機制，并建立了電催化模型來預測電催化劑的活性。在電催化模型中全面討論了對稱和不對稱機理。前者是指由Li2S4直接生成Li2S2，而后者則經歷了有Li2S3的路徑。LiSy?自由基的吸附吉布斯自由能是確定SRR過電位和速率決定步驟的關鍵描述符。因此，綜合考慮了三個描述符(ΔG(LiS3?*)、ΔG(LiS2?*)和ΔG(LiS?*))，構造了一個區域圖模型來可視化過電位和速率決定步驟。該研究在原子水平上建立了SRR電催化模型，加深了對SRR機理的理解，從而可以實現先進SRR催化劑的合理設計。

審核編輯：郭婷