在本系列的第1部分中,我們將了解如何設(shè)計(jì)基于直接數(shù)字頻率合成(DDFS)原理的非常精確的正弦波發(fā)生器,但在浮點(diǎn)DSP處理器上通過軟件實(shí)現(xiàn)。在第 2 部分中,我們將介紹如何在軟件中實(shí)現(xiàn)高精度 NCO。
構(gòu)建具有與最佳模擬振蕩器相似或更好的失真性能的高精度交流音發(fā)生器,如最著名的惠普分析儀或應(yīng)用筆記AN-1323中所述,即使專用于音頻頻譜(直流至20 kHz范圍),也不是一件小事。然而,如前所述,使用嵌入式處理器的足夠算術(shù)精度執(zhí)行相位計(jì)算(ωt)和正弦函數(shù)(sin(ωt))近似的完整軟件實(shí)現(xiàn)肯定有助于最大限度地減少量化副作用,噪聲和由此產(chǎn)生的雜散。這意味著圖2中的所有NCO功能塊都轉(zhuǎn)換為代碼行(無VHDL!),以實(shí)現(xiàn)滿足實(shí)時(shí)約束的軟件版本,以確保最小采樣率和所需的頻率帶寬。
對(duì)于相位到正弦幅度轉(zhuǎn)換引擎,完整的LUT方案或任何變化都需要太多的內(nèi)存或太多的插值操作才能實(shí)現(xiàn)完美的正弦一致性。相反,正弦近似的多項(xiàng)式方法允許使用成本非常低的通用DSP,從而提供了非常好的復(fù)雜度與精度權(quán)衡。多項(xiàng)式級(jí)數(shù)擴(kuò)展也非常有吸引力,因?yàn)樗鄬?duì)簡(jiǎn)單,并且能夠在選擇冪級(jí)數(shù)類型時(shí)提供充分的靈活性,為給定精度定制算法。它不需要大的內(nèi)存空間,少于100行SHARC DSP裝配線,只需要幾個(gè)RAM位置來存儲(chǔ)多項(xiàng)式系數(shù)和變量,因?yàn)檎抑祪H在采樣時(shí)計(jì)算。
首先,正弦近似函數(shù)的明顯選擇是使用具有適當(dāng)順序的直泰勒/麥克勞林冪級(jí)數(shù)來滿足目標(biāo)精度。但是,由于冪級(jí)數(shù)往往會(huì)在端點(diǎn)上失去有效性,因此在執(zhí)行任何多項(xiàng)式計(jì)算之前,必須將參數(shù)輸入范圍減小到較小的間隔。如果不減少參數(shù)范圍,函數(shù)域(如 [–π, +π] )上的高精度只能通過非常高階多項(xiàng)式來支持。因此,需要將一些變換應(yīng)用于初等函數(shù)以獲得簡(jiǎn)化的參數(shù),例如 sin(|x|) = sin(f + k × π/2) 和 sin(f) = sin(x – k × π/2) 為 0 ≤f《π/2。因此,三角函數(shù)應(yīng)格外小心,以避免減法抵消,這將導(dǎo)致精度嚴(yán)重?fù)p失并產(chǎn)生災(zāi)難性結(jié)果,尤其是在算術(shù)精度較差的情況下。在我們的例子中,當(dāng)相位輸入很大或接近π/2的整數(shù)倍時(shí),可能會(huì)發(fā)生這種情況。
除了周期性和模-2π重復(fù)之外,sin(x)函數(shù)的對(duì)稱性質(zhì)還可以用于進(jìn)一步縮小近似范圍。鑒于正弦函數(shù)在區(qū)間 [0, 2π] 的點(diǎn) x = π 上是反對(duì)稱的,因此可以使用以下關(guān)系:
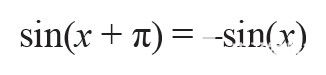
將范圍減小到 [0, π]。以同樣的方式,sin(x) 顯示了區(qū)間 [0, π] 由 x = π/2 定義的直線的對(duì)稱性,使得:
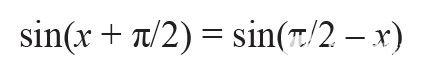
對(duì)于區(qū)間 [0, π/2] 中的 x,這進(jìn)一步減小了角度輸入近似范圍。進(jìn)一步將參數(shù)簡(jiǎn)化為較小的區(qū)間(如 [0, π/4] 以提高精度是沒有效率的,因?yàn)樗枰瑫r(shí)計(jì)算正弦和余弦函數(shù),這是由共同三角關(guān)系決定的:sin(a+b) = sin(a) × cos(b) + cos(a) × sin(b),這對(duì)于生成正交音來說是值得的。
ADI公司的ADSP-21000系列應(yīng)用手冊(cè)第1卷介紹了一種幾乎理想的(用于嵌入式系統(tǒng))正弦逼近函數(shù),該函數(shù)基于為首款A(yù)DI DSP浮點(diǎn)處理器(即ADSP-21020)編寫的優(yōu)化功率級(jí)數(shù),該處理器基本上是一個(gè)SHARC內(nèi)核。sin(x) 的這種實(shí)現(xiàn)依賴于由 Hart 等人發(fā)表的最小最大多項(xiàng)式近似4,并由 Cody 和 Waite5 改進(jìn)用于浮點(diǎn)運(yùn)算,以減輕舍入誤差并避免發(fā)生前面提到的取消。最小最大值方法依賴于切比雪夫多項(xiàng)式和雷梅茲交換算法來確定所需最大相對(duì)誤差的系數(shù)。如圖 3 中的 MATLAB 所示,與 Taylor 的七階泰勒多項(xiàng)式相比,設(shè)定系數(shù)的微小變化會(huì)導(dǎo)致最小最大值的精度顯著提高.6 為了獲得最佳精度與速度權(quán)衡,此正弦近似函數(shù)的角度輸入范圍縮小到 [–π/2 到 +π/2] 區(qū)間,并且軟件例程包括一個(gè)高效的范圍縮小濾波器, 約占總“正弦”子例程執(zhí)行時(shí)間的 30%。
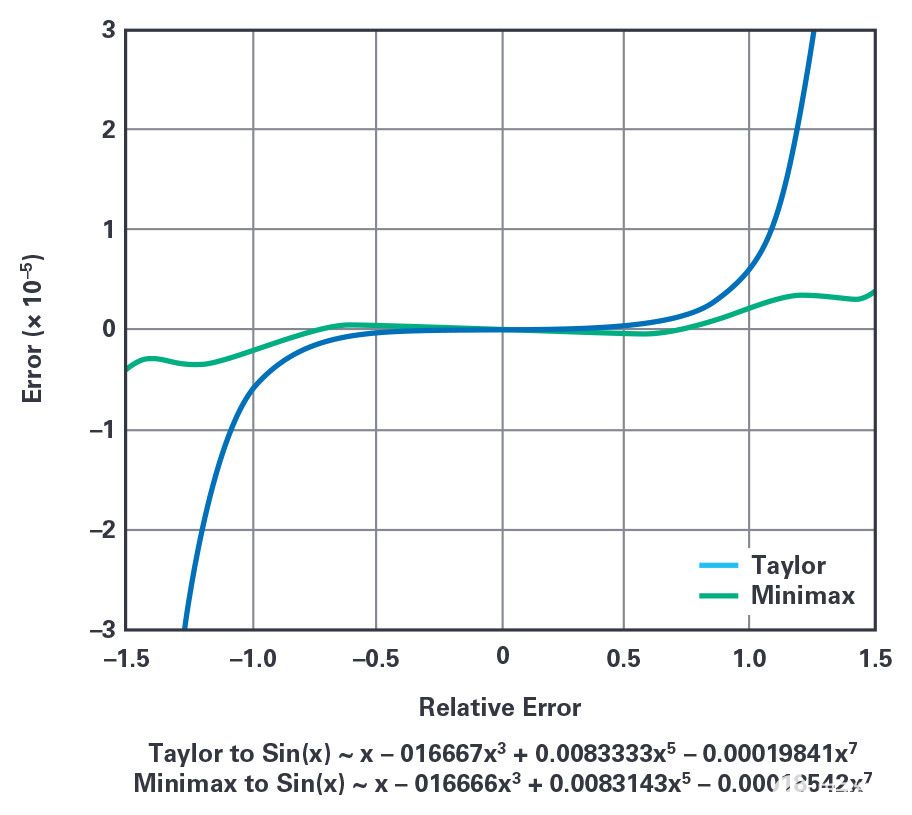
圖3.與在 0 左右定義的 Taylor-MacLaurin 方法不同,最小最大值正弦近似方法最小化并均衡了 [–π/2 至 +π/2] 區(qū)間內(nèi)的最大相對(duì)誤差。
雖然所有的計(jì)算都可以用32位定點(diǎn)算法執(zhí)行,但數(shù)學(xué)計(jì)算最常見和最方便的格式,特別是在處理長數(shù)時(shí),多年來一直是IEEE 754浮點(diǎn)標(biāo)準(zhǔn)。當(dāng)時(shí),根本沒有單芯片浮點(diǎn)DSP處理器,只有簡(jiǎn)單的浮點(diǎn)乘法器和ALU計(jì)算IC,例如ADSP-3212和ADSP-3222。這種格式取代了計(jì)算機(jī)行業(yè)的大多數(shù)專有格式,并成為所有SHARC DSP處理器的原生格式,包括單精度32位、擴(kuò)展精度40位,以及最近ADSP-SC589和ADSP-SC573的雙精度64位。
SHARC 40 位擴(kuò)展單精度浮點(diǎn)格式及其 32 位尾數(shù)為這種正弦波生成應(yīng)用提供了足夠的精度 (u 2–32),為了保持相等,Cody 和 Waite 表明,15 階多項(xiàng)式適用于 32 位的整體精度,在 [0 到 +π/2] 輸入域上均勻分布誤差。最小化操作次數(shù)并保持準(zhǔn)確性的最后一個(gè)調(diào)整是實(shí)現(xiàn)多項(xiàng)式計(jì)算的霍納規(guī)則,這是一種快速冪法,用于評(píng)估一個(gè)點(diǎn)的多項(xiàng)式,例如:
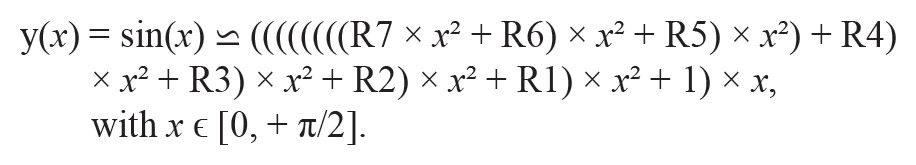
R1 到 R7 是多項(xiàng)式級(jí)數(shù)的 Cody 和 Waite 系數(shù),只需要 8 次乘法和 7 次加法即可計(jì)算任何輸入?yún)?shù) ε[0, π/2] 的正弦函數(shù)。以匯編子例程形式編寫的完整 sin(x) 近似代碼在 SHARC 處理器上以大約 22 個(gè)內(nèi)核周期執(zhí)行。原始程序集子例程經(jīng)過修改,以便在獲取 40 位多項(xiàng)式浮點(diǎn)系數(shù)時(shí)同時(shí)執(zhí)行雙內(nèi)存訪問,以節(jié)省六個(gè)周期。
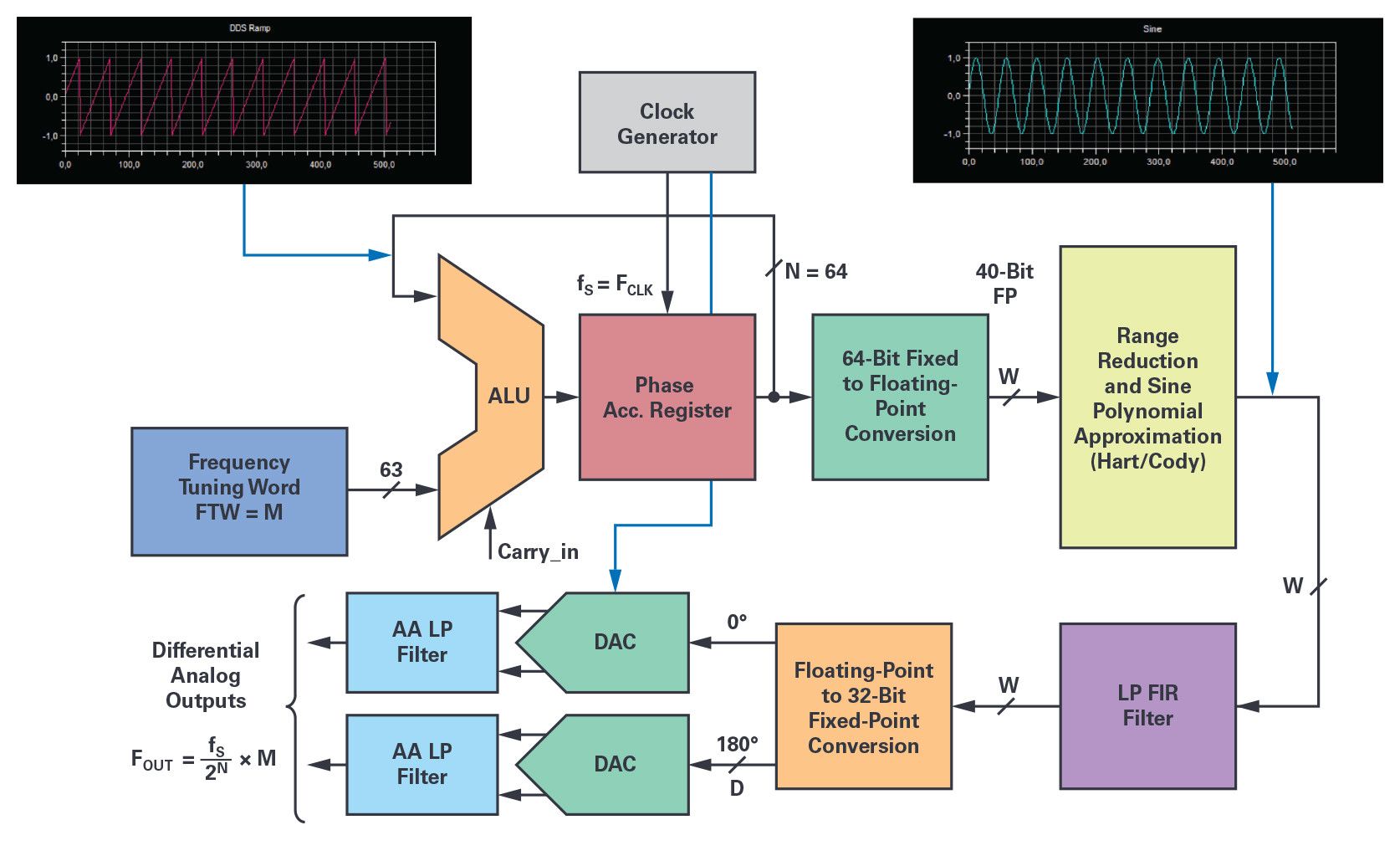
圖4.DDS軟件簡(jiǎn)化框圖給出了數(shù)據(jù)算術(shù)格式和處理元件之間各種量化步驟的位置。
NCO 64 位相位累加器本身正在利用雙精度 2 補(bǔ)碼分?jǐn)?shù)格式的 SHARC 32 位 ALU 來執(zhí)行。一個(gè)完整的相位累加器執(zhí)行和內(nèi)存更新需要 11 個(gè)內(nèi)核周期,因此,每個(gè) NCO 輸出樣本在大約 33 個(gè)內(nèi)核周期內(nèi)生成。
圖4中的圖表顯示了基于DSP的軟件NCO的功能塊實(shí)現(xiàn),并參考了每個(gè)階段的算術(shù)格式精度。此外,信號(hào)模擬重建需要一個(gè)或兩個(gè)DAC及其模擬抗混疊濾波器電路,并實(shí)現(xiàn)完整的DDFS。處理鏈的關(guān)鍵要素是:
64位相位累加器(帶溢流的SHARC ALU雙精度加法);
64位小數(shù)定點(diǎn)到40位FP轉(zhuǎn)換模塊;
范圍縮小塊 [0 到 + π/2] 和象限選擇(科迪和韋特);
用于相位到幅度轉(zhuǎn)換的正弦近似算法(Hart);
–1.0 至 +1.0 范圍內(nèi)的 sin(x) 重建和歸一化階段;
LP FIR 濾波器和 sin(x)/x 補(bǔ)償(如有必要);
以及 40 位 FP 到 D 位定點(diǎn)轉(zhuǎn)換和縮放功能,以適應(yīng) DAC 數(shù)字輸入。
可以在NCO的輸出端放置一個(gè)可選的數(shù)字低通濾波器,以消除可能在目標(biāo)頻帶中折疊的任何雜散和噪聲。或者,該濾波器可以提供插值和/或反sin(x)/x頻率響應(yīng)補(bǔ)償,具體取決于為模擬重建選擇的DAC。這種低通FIR濾波器可以使用MATLAB濾波器設(shè)計(jì)器工具進(jìn)行設(shè)計(jì)。例如,假設(shè)采樣頻率為48 kSPS,直流至20 kHz帶寬,帶內(nèi)紋波為0.0001 dB,帶外衰減為–150 dB,則可以使用40位浮點(diǎn)系數(shù)實(shí)現(xiàn)高質(zhì)量的等紋波濾波器。由于只有 99 個(gè)濾波器系數(shù),其總執(zhí)行時(shí)間將在單指令、單數(shù)據(jù) (SISD) 單計(jì)算單元模式下消耗約 120 個(gè) SHARC 內(nèi)核周期。數(shù)字濾波后,DMA使用其中一個(gè)DSP同步串行端口將計(jì)算出的樣本對(duì)發(fā)送到DAC。為了獲得更好的速度性能,還可以使用大型乒乓內(nèi)存緩沖區(qū)鏈接 DMA 操作,以支持按塊操作進(jìn)行處理。例如,塊數(shù)據(jù)大小可以等于 FIR 數(shù)據(jù)延遲線的長度。
NCO 的最終調(diào)整以實(shí)現(xiàn)最佳 SFDR
如前所述,NCO受到雜散的影響主要是由于相位累加器輸出的截?cái)啵约霸谳^小程度上,由于通過計(jì)算或制表獲得的正弦值進(jìn)行的幅度量化。相位截?cái)嘁鸬恼`差通過相位調(diào)制(鋸齒波)在載波頻率附近產(chǎn)生雜散,而正弦幅度量化會(huì)導(dǎo)致諧波相關(guān)的雜散,盡管長期以來被認(rèn)為是隨機(jī)誤差和噪聲。今天,相位累加器的操作在數(shù)學(xué)上是完美的,正如Henry T. Nicholas和H. Samueli的技術(shù)論文7中所描述的那樣。經(jīng)過徹底分析后,提出了一個(gè)模型,使得相位累加器被認(rèn)為是離散相位采樣置換發(fā)生器,從中可以預(yù)測(cè)頻率雜散。無論相位累加器參數(shù)(M、N、W)如何,相序的長度都等于
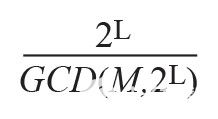
(其中GCD是最大公約數(shù))由頻率調(diào)諧字M的最右邊位位置L決定,如圖4所示。因此,L 的值定義了序列類,每個(gè)序列類共享自己的一組相位分量,但根據(jù)
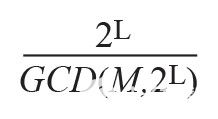
率。這些在時(shí)域中生成的截?cái)嘞辔粯颖拘蛄杏糜谕ㄟ^DFT確定頻域中每條雜散線的相應(yīng)位置和幅度。這些序列還表明,M(FTW)的奇數(shù)值表現(xiàn)出最低頻率雜散的幅度,并建議對(duì)相位累加器進(jìn)行簡(jiǎn)單的修改,只需在FTW中添加1 LSB即可滿足這些最小條件。這樣,無論相位累加器的M值和初始內(nèi)容如何,相位累加器輸出序列都被迫始終具有相同的2N相位元件。然后,最差雜散音幅度的電平降低3.922 dB,等于SFDR_min(dBc)= 6.02 × W。Nicholas改進(jìn)的相位累加器為NCO帶來了幾個(gè)好處,因?yàn)槭紫人薋TW最右邊太接近其MSB(FMCW應(yīng)用中的頻率掃描)的情況,其次,它使雜散的幅度與頻率調(diào)諧字M無關(guān)。通過在采樣速率fS下切換ALU LSB,可以在軟件中輕松實(shí)現(xiàn)這種修改,可以模擬相位累加器的相同行為,就像FTW LSB設(shè)置為邏輯1一樣。當(dāng)相位累加器大小N = 64位時(shí),1/2 LSB偏移可以被認(rèn)為是關(guān)于所需頻率FOUT精度的可忽略不計(jì)的誤差。
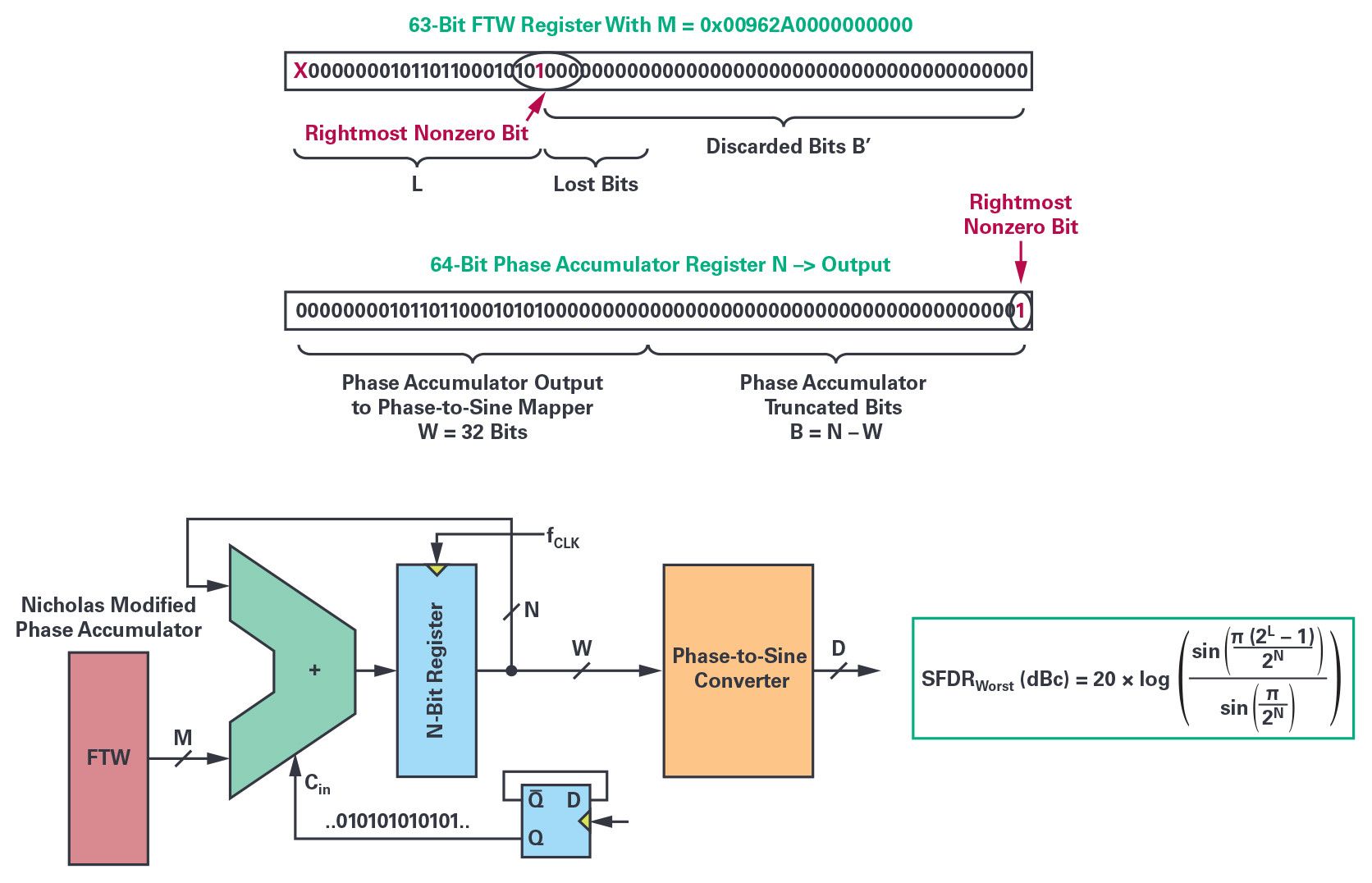
圖5.FTW 最右邊的非零位的位置設(shè)置了理論上的 SFDR 最壞情況水平。尼古拉斯修改的相位累加器解決了N的任何值的問題,并使NCO的SFDR最大化。
輸出相位字W為32位時(shí),相位截?cái)鄬?dǎo)致的最大雜散幅度被限制在–192 dBc!正弦采樣值的有限量化也會(huì)導(dǎo)致另一組頻率雜散,它通常被認(rèn)為是噪聲,并通過眾所周知的關(guān)系SNRq(dB)= 6.02 × D + 1.76進(jìn)行估計(jì)。由于相位-正弦幅度轉(zhuǎn)換算法級(jí)的近似誤差,必須將其添加到寄生元件中,但是,考慮到在選擇相位-正弦近似算法和計(jì)算精度時(shí)非常謹(jǐn)慎,該誤差被認(rèn)為是可以忽略不計(jì)的。
這些結(jié)果表明,我們的軟件正弦NCO的線性度和噪聲都處于理論水平,遠(yuǎn)遠(yuǎn)超出了測(cè)試市場(chǎng)上大多數(shù)高精度ADC所需的閾值。信號(hào)鏈中最后一個(gè)但最關(guān)鍵的元件還有待找到:重建DAC及其互補(bǔ)模擬抗混疊濾波器以及相關(guān)的驅(qū)動(dòng)器電路,這些電路很容易滿足預(yù)期的性能水平。
在本系列的第3部分中,我們將介紹如何選擇重建DAC并完成DDFS系統(tǒng)。
審核編輯:郭婷
-
處理器
+關(guān)注
關(guān)注
68文章
19342瀏覽量
230227 -
dsp
+關(guān)注
關(guān)注
553文章
8030瀏覽量
349318 -
振蕩器
+關(guān)注
關(guān)注
28文章
3839瀏覽量
139167
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
請(qǐng)問ADS1263能做到多高精度?實(shí)現(xiàn)高精度應(yīng)該注意什么?
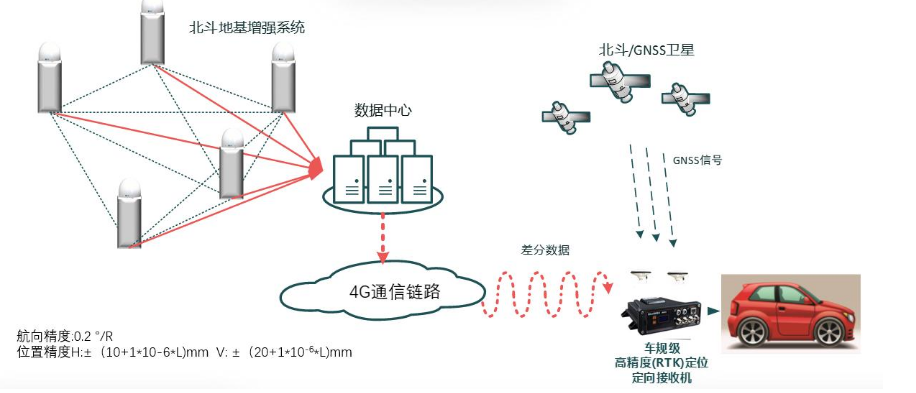
物聯(lián)網(wǎng)系統(tǒng)中高精度RTK定位方案的實(shí)現(xiàn)_高精度定位模塊
VS高精度電壓傳感器
探索UWB技術(shù)的獨(dú)特優(yōu)勢(shì):實(shí)現(xiàn)高精度定位

如何在MSP430?上實(shí)現(xiàn)內(nèi)置振蕩器的高精度定時(shí)器

如何在激光雷達(dá)和接近檢測(cè)中利用高速比較器提高精度

什么是高精度定位平板?
高精度滾珠絲桿在航空航天技術(shù)中實(shí)現(xiàn)精準(zhǔn)對(duì)接!

北斗高精度定位終端的工作原理和精度范圍

mcsdk無法做高精度位置控制如何解決?
納秒激光焊接機(jī)如何實(shí)現(xiàn)高精度焊接

輪廓測(cè)長|中圖儀器SJ51系列測(cè)長機(jī)實(shí)現(xiàn)高精度二維長度測(cè)量

輪廓測(cè)長|中圖儀器SJ51系列測(cè)長機(jī)實(shí)現(xiàn)高精度二維長度測(cè)量
電感多少精度算高精度
輪廓測(cè)長|中圖儀器SJ51系列測(cè)長機(jī)實(shí)現(xiàn)高精度二維長度測(cè)量





 如何在軟件中實(shí)現(xiàn)高精度NCO
如何在軟件中實(shí)現(xiàn)高精度NCO










評(píng)論