(一)非線性系統的模型
當信號幅度很小時,模擬和射頻電路可以通過線性模型來近似,不過,小信號線性模型無法預測系統的非線性。
當需要考慮無記憶系統的非線性時,其輸入/輸出特性可以近似為:
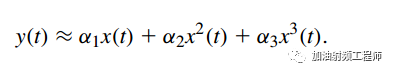
當信號很小時,后面兩項可以忽略不計,因此此時,α1即為系統的小信號增益。
設:
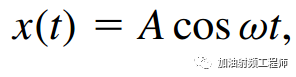
將上式代入輸入/輸出特性曲線,可得到:
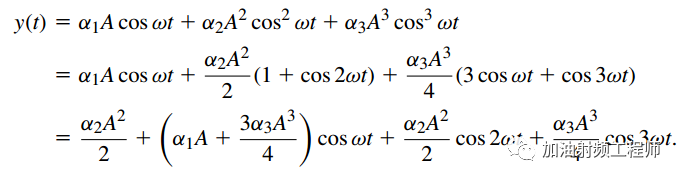
由上式可知,當輸入為小信號時,系統的增益為
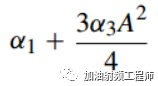
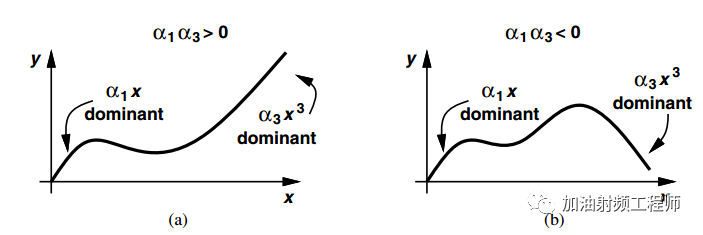
這邊, α1 和α3的符號相反。
因為,如果α1 和α3的符號相同,則當信號足夠大時,系統的增益也會變的很大,這是不現實的。
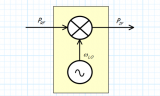
我們熟知的射頻器件,比如說放大器等,在大信號輸入時,增益都會壓縮的。如下圖所示。當 α1α3 < 0 時,信號x(t)=A cos ωt輸入到系統后的增益隨著 A 上升而下降。
(二) 1dB壓縮點的定義
可以通過“1-dB 壓縮點”來衡量增益下降的程度。
“輸入1-dB 壓縮點”定義為導致增益下降 1 dB 的輸入信號電平,此時輸出電平 Aout 在 1-dB 壓縮點(Ain,1dB) 處低于其理想值 1dB。如下圖所示。
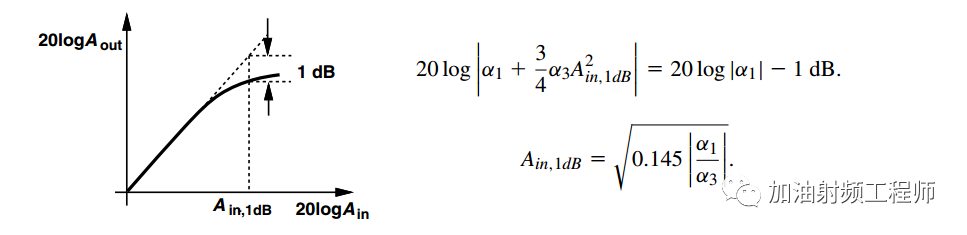
那1dB壓縮點代表什么呢?
20log((0.89*A)/A)=-1dB。
所以,1dB壓縮點代表系統增益下降約11%。
(三)系統增益壓縮后的影響
系統增益壓縮后,真的有關系么?
這要分情況討論。
case1:
如果信號的幅度攜帶信息,那這個時候,信號會因壓縮而失真,這個時候系統對增益壓縮的容忍度是很低的。

case2:
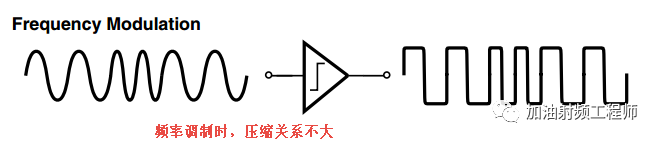
如果信號的幅度不攜帶信息(比如頻率調制),則可以容忍增益壓縮。因為系統增益壓縮了,代表輸入信號足夠大,接收機肯定能接收并解調出這個信號。
case3:
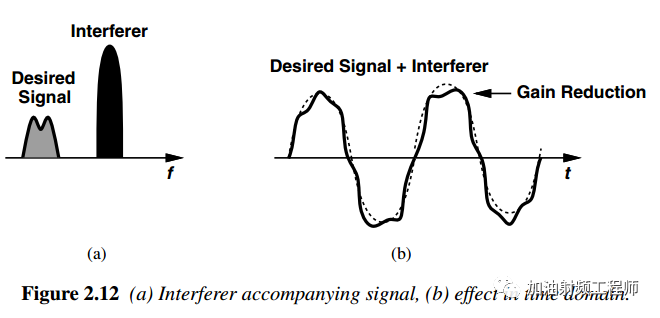
如果有用信號幅度比較小,但是旁邊有比較大的干擾信號,如下圖所示,這兩個信號同時被接收機接收。這時,則會產生不利影響。
因為,雖然有用信號本身很小,但是因為干擾信號的存在,接收機的增益還是會被壓縮。
這個時候,接收機的靈敏度會降低,即使在頻率調制下也是如此。
(四)case3時的理論計算和仿真驗證
那在case3時,到底會有多少影響呢?
假設,輸入信號為:

經過一番推導,如下圖所示:

所以,對于有用信號,其增益為:
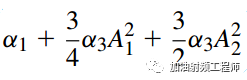
,因為A1<
對于干擾信號,其增益為:
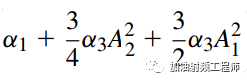
,因為A1<
所以 ,當 α1α3 < 0時,有用信號的增益和干擾信號的增益都會下降,但是下降的程度不太一樣。
由下面的推導可知,當干擾信號的增益下降1dB時,有用信號的增益下降2.13dB。

現在用ADS進行仿真,看仿真值和理論計算值是否能吻合。
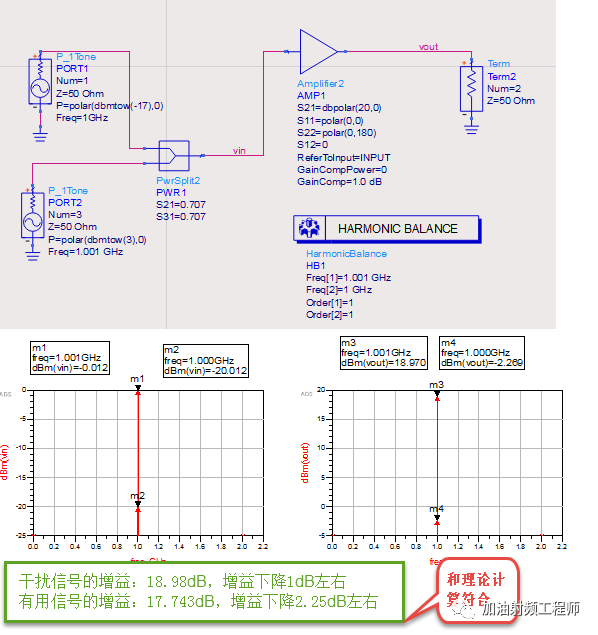
由上圖仿真結果可知,仿真值和理論值符合。
當然,這也還只是仿真和理論值,如果要確認的話,還得實測。
有條件的朋友,可以在實驗室搭個環境測試一下。
審核編輯:湯梓紅
-
非線性系統
+關注
關注
0文章
20瀏覽量
7879 -
射頻器件
+關注
關注
7文章
125瀏覽量
25545
原文標題:來來來,看看1dB壓縮點
文章出處:【微信號:加油射頻工程師,微信公眾號:加油射頻工程師】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
功率放大器P1dB、P3dB和PSat、功率附加效率(PAE)指標釋義
請問hmc451Alp3增益和1dB壓縮點實測與手冊不符是為什么?
請問9361在LPF前端的1dB壓縮點是多少?
AD8330輸入1db壓縮點和輸出三階互調點的疑問求解
1dB壓縮點與IIP3到底有什么關系
功率放大器P1dB、P3dB和PSat指標釋義

解讀RF放大器規格:輸出電壓/電流和1dB壓縮點
線性度的基本概念(1dB壓縮點,IP3,OP3)
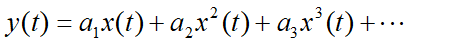




 1dB壓縮點的定義
1dB壓縮點的定義











評論