要計算FFT（快速傅立葉變換），只需聽聽。人耳自動且不由自主地執行一項計算，這需要多年的數學教育才能完成。耳朵通過將聲音（隨時間傳播和穿過大氣的壓力波）轉換為頻譜來制定轉換，將聲音描述為一系列不同音高的體積。然后，大腦將這些信息轉化為感知的聲音。

類似的轉換可以在相同的聲波或幾乎任何其他隨時間變化的波動信號上使用數學方法完成。傅里葉變換是用于進行此轉換的數學工具。簡單地說，傅里葉變換將時域中的波形數據轉換為頻域。傅里葉變換通過將原始基于時間的波形分解為一系列正弦項來實現這一點，每個項都有獨特的幅度、頻率和相位。實際上，這個過程將時域中難以用數學描述的波形轉換為一系列更易于管理的正弦函數，當它們加在一起時，可以精確地再現原始波形。繪制每個正弦項的幅度與其頻率的關系圖可以創建一個功率譜，這是頻域中原始波形的響應。圖1說明了這種時域轉換概念。

傅里葉變換已成為不同科學領域的強大分析工具。在某些情況下，傅里葉變換可以提供一種求解描述對電、熱或光的動態響應的笨拙方程的方法。在其他情況下，它可以識別對波動信號的常規貢獻，從而有助于理解天文學，醫學和化學中的觀測結果。也許是因為它的有用性，傅里葉變換已被改編用于個人計算機。已經開發出算法，將個人計算機及其評估大量數字的能力與傅里葉變換聯系起來，為頻域中波形數據的表示提供基于個人計算機的解決方案。但是您應該在傅里葉分析軟件中尋找什么？是什么讓一個軟件包在功能、靈活性和準確性方面優于另一個軟件包？本應用筆記將介紹并解釋此類軟件包的一些元素，試圖消除圍繞這個強大分析工具的神秘面紗。

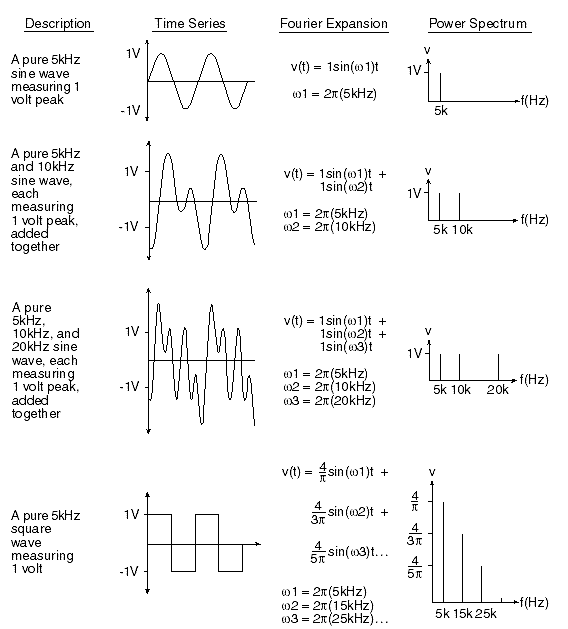
圖 1 — 圖示傅里葉變換

DATAQ Instruments的WinDaq波形瀏覽器（WWB）回放軟件包含一個傅里葉變換算法，該算法是本應用筆記的模型，包括本文討論的傅里葉變換的所有元素。本說明中介紹的所有圖形和概念也派生自 WWB 傅里葉變換實用程序。

變形三重奏

在計算機出現之前，傅里葉變換的數值計算是一項非常勞動密集型的任務，因為如此大量的算術必須用紙和鉛筆進行。隨著計算機和程序的開發，這些計算變得更加實用，以實現傅里葉分析的新方法。其中一種方法是由James W. Cooley和John W.Tukey 1于1965年開發的，他們的工作導致了一種稱為快速傅里葉變換的程序的開發。快速傅里葉變換 （FFT） 是一種生成傅里葉變換的計算效率高的方法。FFT的主要優點是速度，它通過減少分析波形所需的計算次數來實現速度。與FFT相關的缺點是可以轉換的波形數據范圍有限，并且需要對波形應用窗口加權函數（待定義）以補償頻譜泄漏（也有待定義）。

FFT的替代方案是離散傅里葉變換（DFT）。DFT 允許您精確定義計算轉換的范圍，從而消除了窗口的需要。不利的一面是，DFT的計算速度比FFT慢。

從時域到頻域的轉換是可逆的。一旦功率譜由前面提到的兩個變換之一顯示，就可以通過計算傅里葉逆變換（IFT）將原始信號重建為時間的函數。這些變換中的每一個都將在以下段落中單獨討論，以填補缺失的背景，并為市場上各種傅里葉分析軟件包之間的比較提供標準。

使用 FFT 生成功率譜

FFT只是DFT的更快實現。FFT 算法將 n 點傅里葉變換減少到大約

（不適用） 日志2（n）

復雜的乘法。例如，直接計算，1，024（即210）數據點的DFT將需要

n 2= 1，024 × 1，024 = 220= 1，048，576

乘法。FFT 算法將其減少到大約

（n/2） log2（n） = 512 × 10 = 5，120

乘法，提高 200 倍。

但速度的提高是以犧牲多功能性為代價的。FFT函數自動對要評估的時間序列施加一些限制，以產生有意義、準確的頻率響應。由于 FFT 函數根據定義使用以 2 為底的對數，因此它要求要評估的時間序列的范圍或長度包含精確等于 2 次方到 n 次方數的數據點總數（例如，512、1024、2048 等）。因此，使用 FFT，您只能評估包含 512 個點、1024 個點或 2048 個點等的固定長度波形。例如，如果時間序列包含 1096 個數據點，則使用 FFT 一次只能評估其中的 1024 個數據點，因為 1024 是小于 1096 的最高 2 次方 n 次方。

由于這種 2 次方到 n 次方的限制，出現了另一個問題。當FFT評估波形時，波形的一部分被包圍為512點，或1024點，依此類推。這些邊界之一還在波形上建立一個起點或參考點，該起點或參考點在確定的間隔后重復，從而定義波形的一個完整周期或周期。任意數量的波形周期，更重要的是，在這些邊界之間可以存在部分波形周期。這就是問題發展的地方。FFT函數還要求要評估的時間序列是相應的周期函數，或者換句話說，時間序列必須包含圖2a所示的整數個周期，以產生準確的頻率響應。顯然，波形包含的點數等于 2 的 n 次方數并以整數個周期結束的可能性充其量是微乎其微的，因此必須采取措施來確保頻域中的準確表示。在我們研究確保頻域精度的方法之前，讓我們仔細看看全部/部分周期數困境。

如果在不包含圖2b所示整數周期的波形上執行FFT，會發生什么情況？

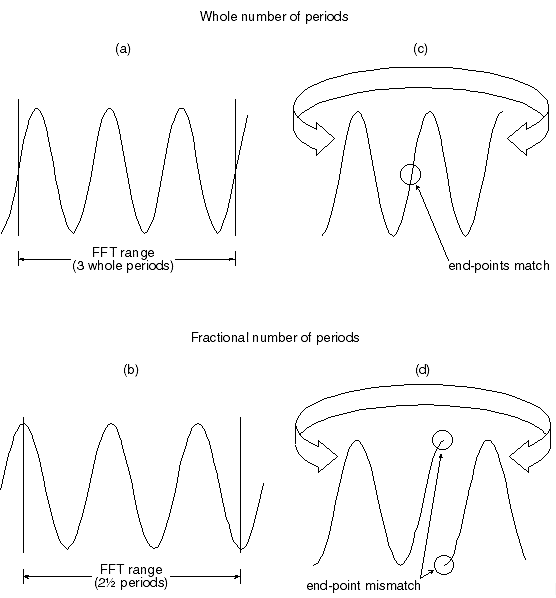
圖 2— 波形連續性與不連續性的示例，避免了復雜的數學解釋。（a） 顯示最佳情況，百萬分之一的波形，其中 FFT 的范圍正好包含整數個周期，從波形平均值開始。該波形具有終點連續性，如（c）所示，這意味著得到的功率譜將是準確的，不需要應用窗口。更典型的遭遇如（b）所示，其中FFT的范圍不包含整數個周期。該波形端點的不連續性（d）意味著產生的功率譜將包含輸入中不存在的高頻分量，需要應用一個窗口來衰減不連續性并提高精度。

將要評估的波形長度視為已展開的環。如果將未卷繞環的兩端重新連接在一起以再次形成一個環，則由整數周期組成的波形將完美地連接在一起，如圖2c所示。然而，如圖2d所示，由分數點數組成的波形不會完美地連接在一起，兩端之間沒有間隙或重疊。因此，FFT將使用端點誤差評估該波形，并生成包含代表端點失配的虛假頻率分量的功率譜。考慮圖3所示的光譜。該圖顯示了振幅和頻率相等的兩個正弦波的功率譜。然而，正確功率譜的峰值似乎有些“分散”。這種不準確性是對不包含整數周期的波形執行FFT的結果。正確功率譜的擴散或“泄漏”效應是由于波形端點的不連續性人為產生的能量。

幸運的是，有一種解決方案可以最大限度地減少這種泄漏效應誤差并確保頻域精度。除了DFT（待定義）之外，唯一的解決方案是在執行FFT之前將時間序列乘以窗口加權函數。大多數窗口加權函數（通常稱為“窗口”）通過將窗口兩端的信號逐漸變細至零來衰減不連續性，如圖5d所示。但是，如果您的波形在窗口的末端出現重要信息，它將被錐形破壞。在這種情況下，必須尋求窗口以外的解決方案。通過窗口方法，FFT處理的周期性錯誤信號將在端點處平滑過渡，從而產生更準確的功率譜表示。存在許多窗口。每個窗口都有不同的特性，使一個窗口在分離頻率上彼此靠近的頻譜分量，或隔離一個比另一個小得多的頻譜分量，或任何任務方面比其他窗口更好。一些流行的窗戶（以其發明者的名字命名）是漢明，巴特利特，漢寧和布萊克曼。漢明窗口提供熟悉的鐘形加權功能，但不會使窗口邊緣的信號歸零。漢明窗口產生了非常好的光譜峰值，但只能減少公平的光譜泄漏。Bartlett窗口提供三角形加權功能，使窗口邊緣的信號歸零。該窗口產生良好、尖銳的光譜峰值，并且還擅長減少光譜泄漏。漢寧窗口提供了一個類似的鐘形窗口（如圖5d所示，與漢寧窗口的形狀非常近似），這也使窗口邊緣的信號為零。漢寧窗口產生了良好的光譜峰值清晰度（與巴特利特窗口一樣好），但漢寧提供了非常好的光譜泄漏減少（優于巴特利特）。布萊克曼窗口提供類似于漢寧的加權功能，但形狀更窄。由于形狀較窄，Blackman窗口在減少光譜泄漏方面效果最好，但權衡只是公平的光譜峰值清晰度。如圖4所示，窗口函數的選擇是一門藝術。這取決于您操縱各種窗口約束之間的權衡的技能，以及您希望從功率譜或其逆中得到什么。顯然，提供多個窗口選擇的傅里葉分析軟件包對于消除FFT固有的頻譜泄漏失真是可取的。

簡而言之，FFT是一種計算快速的方法，可以根據波形的2到n次方數據點部分生成功率譜。這意味著在功率譜中繪制的點數不一定像最初預期的那么多。FFT還使用一個窗口來最小化由于端點不連續性引起的功率譜失真。然而，這個窗口可能會衰減出現在待評估時間序列邊緣的重要信息，并扭曲IFT操作（待定義）的結果，如圖5d所示。由于FFT固有的這些限制，您正在考慮的傅里葉分析軟件包是否提供FFT以外的解決方案？

另一種解決方案放棄了窗口化，轉而允許用戶精確定義計算傅里葉變換的范圍。這種方法取消了 2 到 n 次方的限制，稱為 DFT。

使用DFT生成功率譜

如果需要以比FFT允許的精度更高的精度變換部分波形，或者當需要非窗口變換時，DFT生成就是答案。例如，如果您正在處理瞬態信號，則邊緣包含重要信息，這些信息在應用窗口解決方案時會失真，這是不可接受的。在這種情況下，您別無選擇，只能使用 DFT。如前所述，DFT允許您調整定義要變換的波形范圍的端點，從而消除了對窗口的需要。這種方法允許評估包含任意數量點的波形，這比固定長度、2 次方到 n 次方 FFT 提供了更大的靈活性。然而，為了防止與非窗口FFT相同的泄漏效應，DFT必須在從波形平均電平交叉開始的整數周期內產生。換句話說，必須調整定義將計算DFT的波形范圍的終點，以包含或定義整數個周期，最好從波形與其平均值交叉的點開始或附近開始。

DFT比FFT具有更多的多功能性和精度。但是，多功能性和精度是以算法增加的計算時間和增加端點定位所花費的時間為代價的。例如，表1比較了使用DATAQ Instruments的WWB傅里葉變換實用程序在相同波形上生成FFT和DFT所需的計算時間差異。顯示的時間以秒為單位，是從沒有數學協處理器的基于 386 的 25 兆赫 PC 獲得的。由于 WWB 傅里葉變換算法使用整數算術，因此數學協處理器對提高性能的作用很小，因此此軟件包不需要。某些軟件包要么需要數學協處理器才能運行，要么強烈建議使用數學協處理器以獲得最佳性能。請注意，DFT 計算時間僅比 FFT 慢大約四倍。這是因為 WWB 實用程序使用與 FFT 非常相似的計算技術來計算 DFT。結果是計算速度比DFT通常需要的標準n2乘法數快得多。

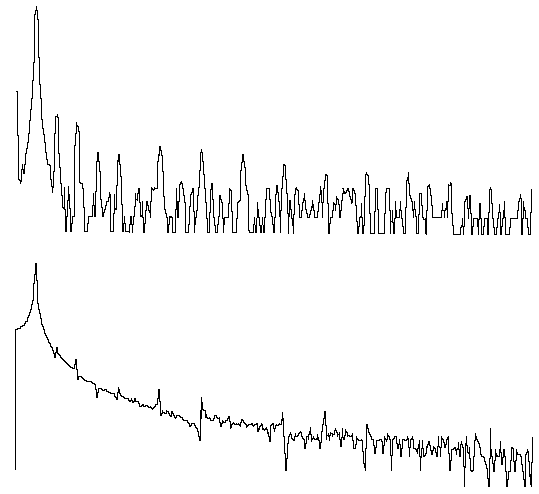
圖 3— 正弦波的頻譜在單個頻率處達到峰值，如上圖頂部所示，當對包含整數周期的波形部分執行 FFT 時。如果FFT是在小數個周期上進行的，頻譜會給出一個非常不同的圖像，如上圖底部所示 - 一個寬峰值導致頻率確定不良和幅度不準確。這些波形是由廉價的函數發生器產生的，它解釋了頻譜中存在的噪聲。

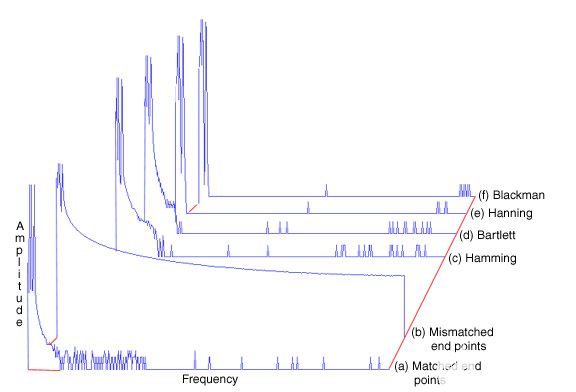
圖 4— 兩個頻率接近但幅度差異很大的正弦波的傅里葉變換很好地說明了窗口選擇的重要性。（a） 顯示了最佳匹配端點變換，其中明確定義了構成原始波形的兩個信號頻率，一個在 90 dB 時為 2.2 Hz，另一個在 46 dB 時為 10.9 Hz。更典型的是，（b）僅顯示端點不匹配的相同波形的變換。請注意，在這個光譜中甚至看不到第二個峰值。顯然需要一個窗口。其余變換說明了各種窗口在抑制頻譜泄漏和恢復丟失頻率分量方面取得的成功程度。每個窗口都應用于原始波形，結果說明了峰值銳度和旁瓣衰減之間的權衡。（c） 顯示漢明窗口。請注意，此窗口永遠不會將信號歸零。（d） 顯示巴特利特窗口，（e） 顯示漢寧窗口，（f） 顯示布萊克曼窗口。對于這個光譜分離的例子，布萊克曼窗口最擅長將較弱的項作為明確定義的峰。

變換 類型點數

512102420484096819216384

FFT0.30.60.91.42.67.3

DFT1.32.03.35.612.6--

表 1 — 各種點變換的計算時間（以秒為單位）。應該提到的是，DFT是根據一系列數據點計算的，該數據點比所示數字少一個。這樣做是為了確保軟件將生成DFT。如果它運行在 2 到 n 次方的數據點數（例如，1024 個），則軟件足夠“智能”，可以識別可以從此數量的數據點生成 FFT 或 DFT。由于DFT意味著更多不必要的計算，因此軟件將采用最少計算的路徑，從而產生FFT。WinDaq能夠使用 FFT 轉換最多 16，384 個數據點，使用 DFT 轉換 8，191 個數據點。

使用IFT生成時間序列

與其他雙邊變換（例如矩形到極坐標）一樣，傅里葉變換在兩個方向上都起作用。如果功率譜（作為頻率的函數）要“向后運行”，則原始信號原則上將被重建為時間的函數。這被稱為傅里葉逆變換（IFT）。你可能會質疑IFT的目的，如果它所做的只是讓你回到你開始的地方。IFT的美妙之處在于它能夠在頻域中編輯功率譜后讓您回到時域。此功能在功率譜濾波應用中非常有用。例如，在許多情況下，需要檢查沒有任何“噪聲”的波形，以扭曲信號的真實性質。這可以通過在執行IFT之前對功率譜應用高通、低通、帶通和陷波濾波器功能來完成。高通濾波器將去除功率譜上小于指定點的所有不需要的頻率分量，低通濾波器將去除所有大于指定點的不需要的頻率分量。帶通濾波器是高通和低通濾波器的組合，用于隔離功率譜上的目標窄帶。陷波濾波器可去除指定點處不需要的頻率分量。圖5顯示了頻域中可能的功率譜編輯類型。濾波操作可以是傅里葉分析軟件包中的一項強大功能。

其他傅里葉分析軟件問題

任何傅里葉分析應用的需求都可以通過基于圖形的軟件包得到最好的滿足，該軟件包允許快速功率譜編輯。除了基本的FFT、DFT和IFT操作外，傅里葉分析軟件包的價值還可以通過附帶的額外“花里胡哨”進一步增強。

支持波形傅里葉分析的軟件包應該能夠以工程單位或相對幅度（分貝）顯示頻率分量的強度，因為轉換功率譜幅度單位可能是一項耗時的任務。

另一個問題是功率譜分辨率。除了速度之外，分辨率是 512 點變換和 16，384 點變換之間的唯一區別。功率譜的范圍始終從直流電平 （0 Hz） 到被變換波形采樣率的一半，因此變換中的點數定義了功率譜分辨率（512 點傅里葉變換的功率譜中有 256 個點，1024 點的傅里葉變換的功率譜中有 512 個點， 等等）。例如，如果要在復雜波形的功率譜中看到單獨的 20 和 21 Hz 頻率分量，則 512 點傅里葉變換可能無法清楚地顯示這些單獨的分量，因為它的整個功率譜僅分為 256 個等間距點，并且所需頻率非常接近。但是，如果變換包含更多點，它將能夠將更多點用于定義緊密間隔的頻率分量。變換中的點數越多，頻率分辨率越好。

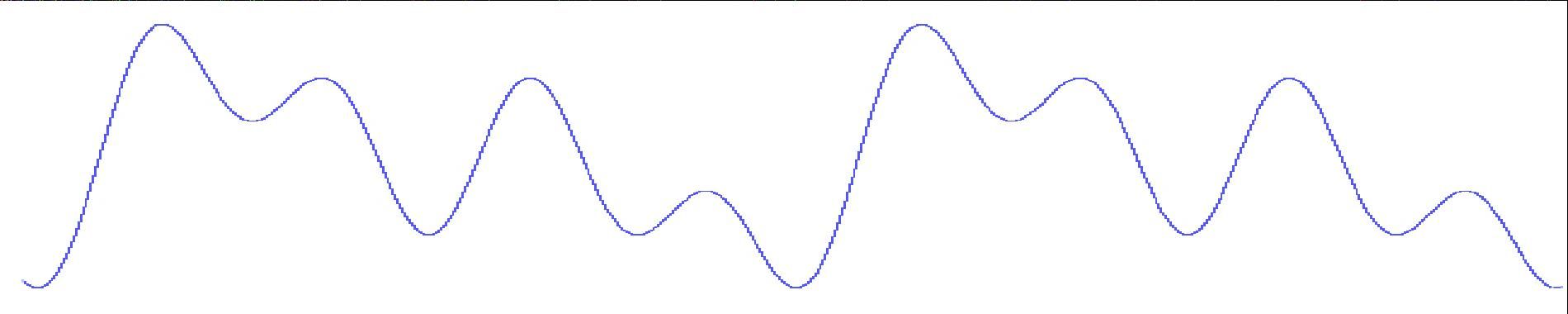
（a） 原始波形

（b） （a）的功率譜

（c） 濾波功率譜

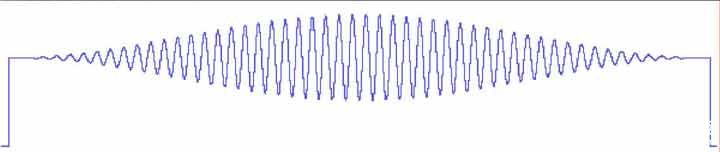
（d） 旅游學院成績

編輯在頻域中進行。（a）所示的波形是包含不良的60 Hz噪聲的20 Hz信號。使用512點FFT生成（b）所示的功率譜。在頻域中，所有大于40 Hz轉折頻率的不良頻率分量（包括60 Hz噪聲）都被編輯掉，或者通過應用低通濾波器（c）將其降低到零。然后從該濾波功率譜生成IFT，產生（d）所示的純20 Hz波形。注意波形的鐘形外觀。這是由于漢寧窗口的應用，這是FFT固有的光譜泄漏困境的解決方案。另請注意漢寧窗口如何將窗口邊緣的信號衰減到零。如果應用了DFT，這種衰減將被消除，20 Hz信號將從頭到尾以全振幅顯示。

一個相關的問題是功率譜放大。所考慮的軟件應該能夠在一個屏幕寬度上顯示整個功率譜，而不管變換中的點數如何。這對于發現頻譜的整體趨勢很有用。通過放大倍率，該軟件還應該允許您選擇功率譜圖的一部分，并使用多個放大倍率因子更仔細地檢查它。1024 × 768 的視頻標準提供 1024 個水平分辨率的圖像元素（像素）。如果執行 512 點傅里葉變換，則變換生成的 256 個點非常適合 1024 像素寬的屏幕。1024 點轉換也是如此，其中 1024 像素寬的屏幕足以包含轉換生成的 512 點。執行大于 2048 個點的變換時會出現此問題。假設執行了 8192 點傅里葉變換。變換生成的 4096 個點比屏幕的 1024 像素寬度寬得多。為了在一個屏幕寬度上獲得整個功率譜，必須應用壓縮系數（在本例中為4倍）。然后必須應用放大倍率以檢查8192點變換全分辨率下的光譜。此外，當應用禁止在單個屏幕寬度上顯示整個功率譜的放大系數時，軟件應允許您一次平移一個屏幕寬度的整個繪圖。

另一個需要考慮的功能是出口設施。是否可以使用您正在考慮的軟件將定義 FFT 圖的坐標導出到 ASCII 文件？此功能允許您復制頻譜以用于其他程序。

您正在考慮的軟件是否允許您在同一波形上快速查看每個窗口的結果？在試驗不同類型的窗口以及每個窗口提供的結果時，這可能是一個方便且節省時間的功能。

最后，軟件包應該能夠進行功率譜平滑。這最好由移動平均實用程序實現。移動平均線是通過從頻譜中獲取兩個或多個數據點，將它們相加，將它們的總和除以添加的數據點總數，將第一個數據點替換為剛剛計算的平均值，然后用第二個、第三個數據點重復這些步驟來實現的，依此類推，直到到達數據末尾。這種簡單的平均技術用于衰減功率譜圖中經常遇到的隨機、小幅度頻率尖峰。

審核編輯：郭婷