很多朋友覺得PID是遙不可及,很神秘,很高大上的一種控制,對(duì)其控制原理也很模糊,只知曉概念性的層面,知其然不知其所以然,那么本期從另類視角來探究微分、積分電路的本質(zhì),意在幫助理解PID的控制原理(PID:P表示比例控制;I表示積分控制;D表示微分控制)。
在認(rèn)清微分、積分電路之前,我們都知道電容的特性:電容的電流超前電壓相位90°,很多教材都這么描述,讓人很費(fèi)解,其本質(zhì)又是什么呢?
要徹底掌握微分、積分電路或PID控制思路,首先得了解電容。
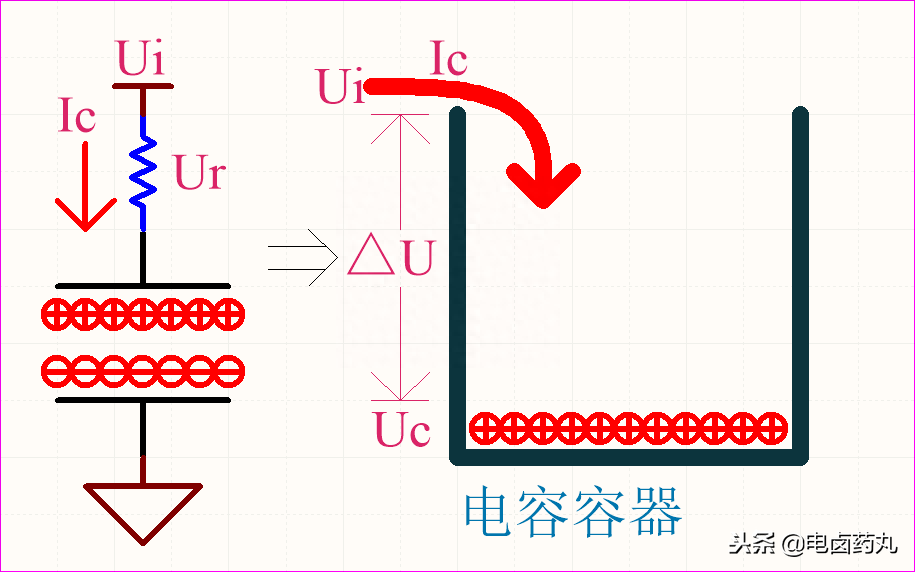
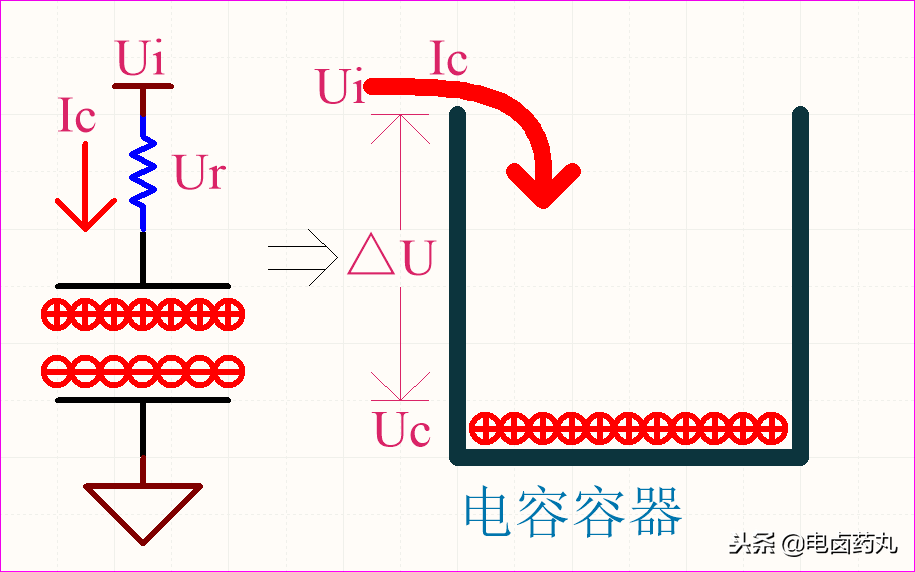
電容就是裝載電荷的容器,從微觀角度看,當(dāng)電荷流入容器時(shí),隨著時(shí)間的變化極間電場逐漸增大;以圖1為例:
①充電開始時(shí)Uc=0V,壓差△U=Ur=Ui,此刻容器內(nèi)無電荷,也就無電場排斥流入的電荷;所以電流Ic最大,表現(xiàn)為容抗最小,近似短路;
②當(dāng)Uc上升,壓差△U開始減小,該過程形成電場,容器開始排斥流入的電荷;電流Ic逐漸減小,表現(xiàn)為容抗逐漸增大;
③當(dāng)Uc=Ui,壓差△U=Ur=0V,此刻容器內(nèi)電場最強(qiáng),以最大排斥力阻止流入的電荷;電流Ic=0,表現(xiàn)為容抗最大,近似開路。
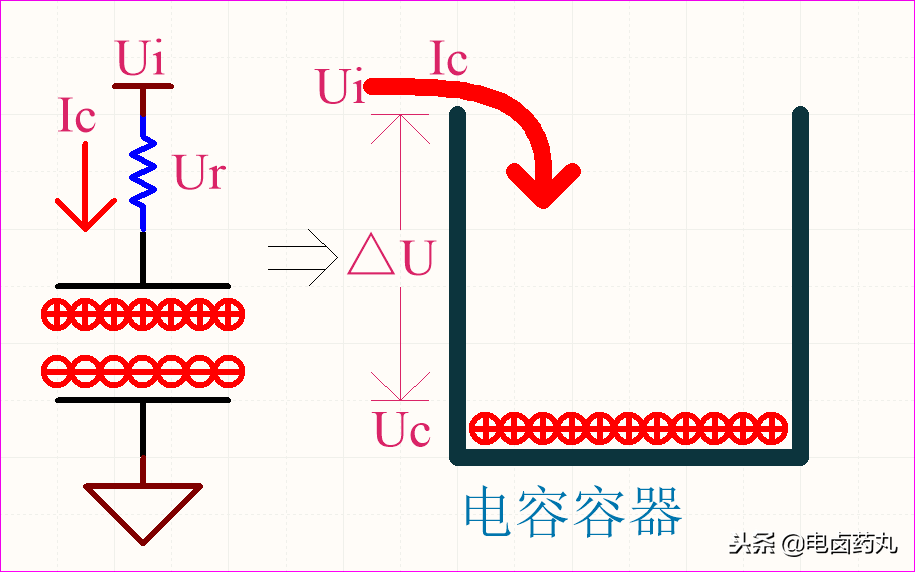
圖1:電容容器充電模型
當(dāng)電荷流出容器時(shí),隨著時(shí)間的變化極間電場逐漸減小;該放電過程的電容可看成是一個(gè)內(nèi)阻為0的電壓源,以圖2為例(移除電源并接地):
①放電開始時(shí)Uc=Ui,此刻容器內(nèi)充滿電荷,因此電場最強(qiáng),而電阻不變,則放電電流Ic最大(方向與充電相反),電阻兩端的電壓Ur=Uc,則Ur=Ui;
②當(dāng)Uc下降,該過程電場減弱,放電電流Ic逐漸減小,Ur=Uc也逐漸減小;
③放電耗盡Uc=0V,此刻容器內(nèi)無電荷,因此無電場,Ur=0V。
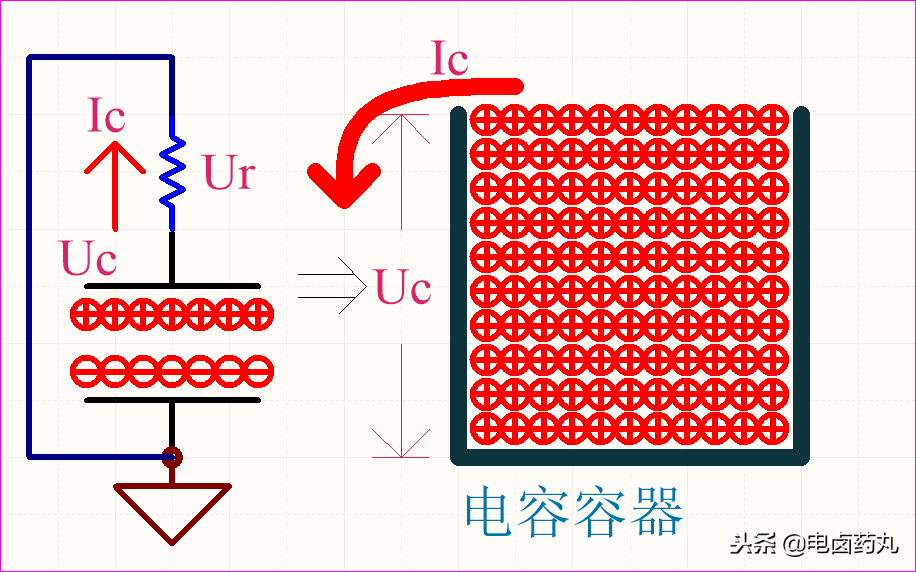
圖2:電容容器放電模型
電容就好比水桶一樣,流入的水流無論是大還是小,水位的變化一定是從最低位開始連續(xù)上升的;而電容內(nèi)的電荷也是逐漸從0開始積累起來的,積累過程與自然常數(shù)e有關(guān)系,這里就不深入討論了。
圖3就是電容充放電的電壓-電流曲線。
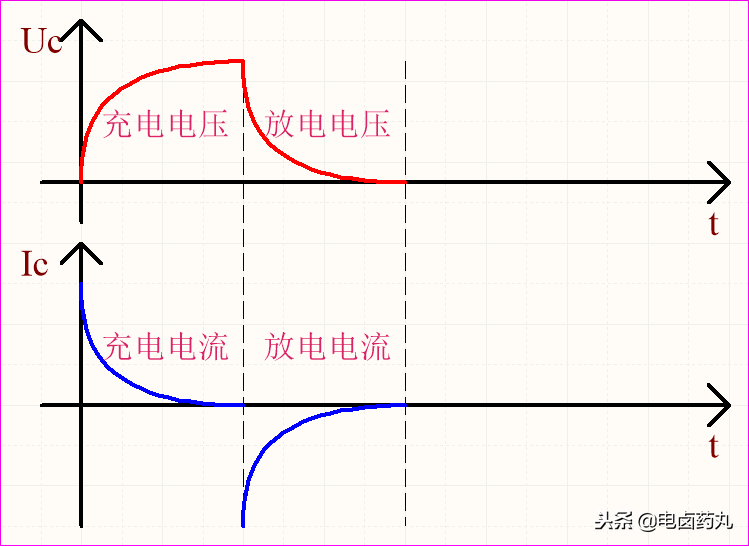
圖3:電容充放電,電壓-電流曲線
聯(lián)系前面的分析,可總結(jié)為:
①電容電壓不能突變,電流可突變(教材的定義是電容的電流與電壓的變化率成正比);
②充電過程中的電容可等效成一個(gè)可變電阻,放電過程中的電容可等效成一個(gè)電壓源;
③電容電流反映的是單位時(shí)間內(nèi)流動(dòng)的電荷量,電容電壓(或電場)反映的是電荷量的多少。通俗的理解就是流動(dòng)的電荷才會(huì)導(dǎo)致電荷量多少的變化(與①相吻合);用數(shù)學(xué)語言描述則是電容的電流超前電壓相位90°;
④電容充放電速度與電容和電阻大小有關(guān)。
對(duì)電容充分了解之后,首先我們先來認(rèn)識(shí)最簡單的分壓電路,如圖4根據(jù)歐姆定律VCC=2.5V,該純阻性的分壓電路就是比例運(yùn)算電路的雛形。
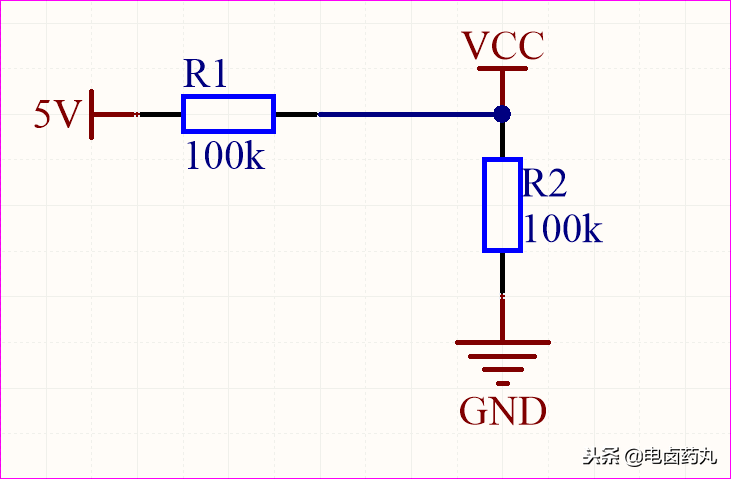
圖4,:分壓電路
如圖5,我們把R2換成104(0.1μF)電容,C1電容充滿電后近似開路,VCC=5V;該電路就是積分運(yùn)算電路的雛形。那么把5V改成信號(hào)源就構(gòu)成了低通濾波電路。
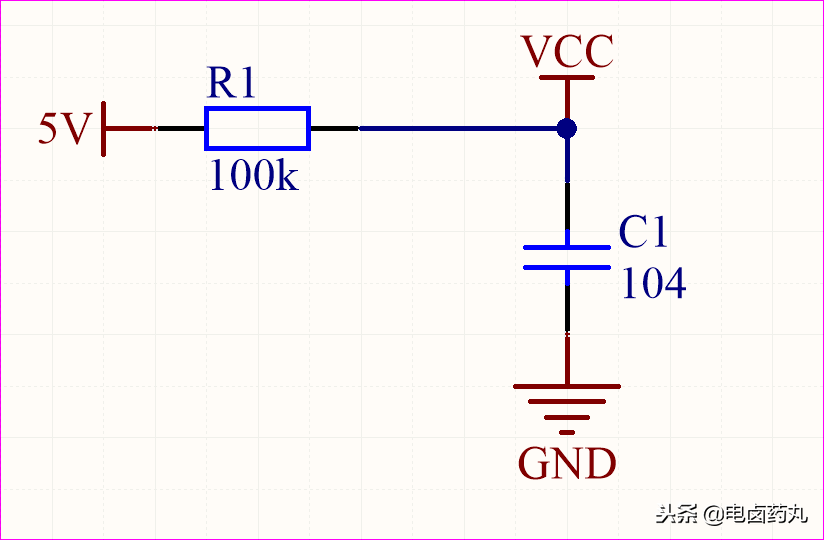
圖5:積分電路
如圖6為上圖的充電波形,紅色表示5V的波形,藍(lán)色表示VCC的波形,因?yàn)殡娙莩潆姇r(shí)的容抗由小變大直至開路,所以分壓VCC也由小變大直至為5V。而且電容充電需要一定的時(shí)間,導(dǎo)致VCC的波形要緩一些。(該5V是開關(guān)電源上電軟啟動(dòng)時(shí)的輸出波形)
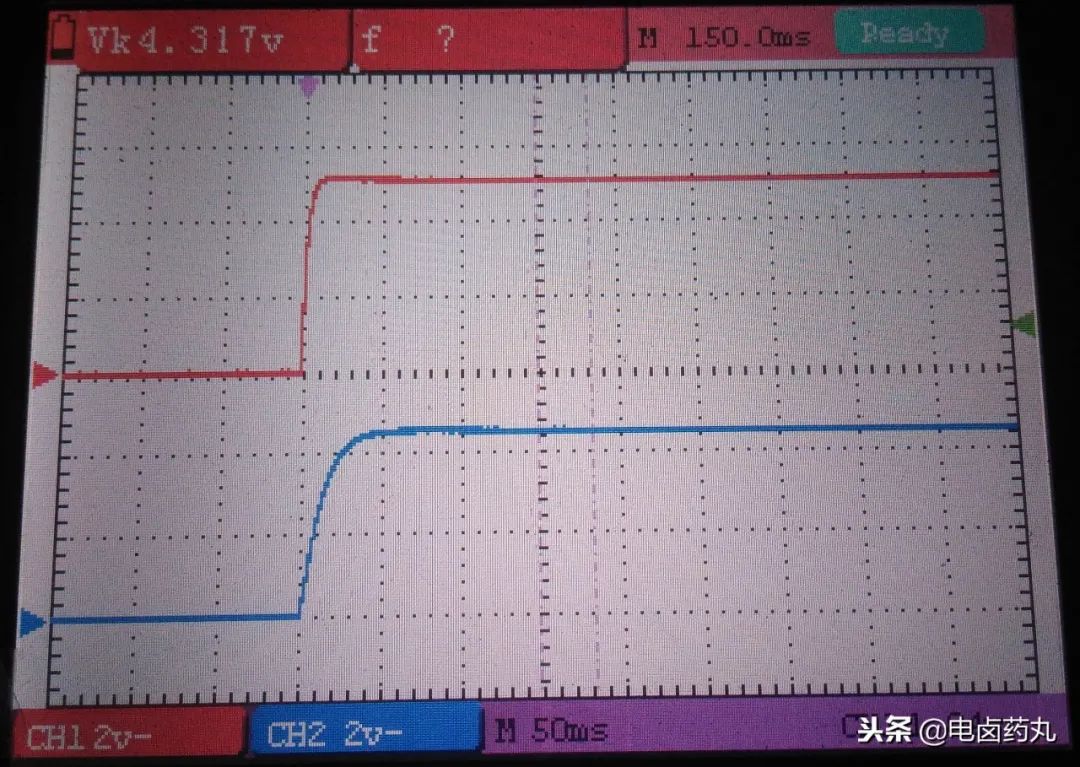
圖6:積分電路波形
把圖4圖5組合就得到圖7的電路,這就是我們經(jīng)常使用的PI電路(比例積分),在參考電壓或分壓電路里很常見,加電容的目的就是增加延時(shí)性,穩(wěn)定VCC的電壓不受5V波動(dòng)而波動(dòng),VCC=2.5V。
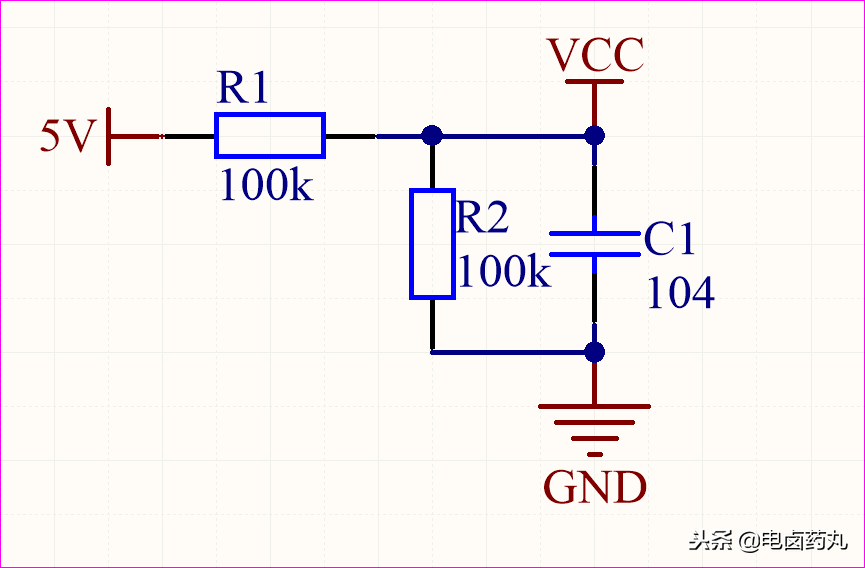
圖7,:PI電路
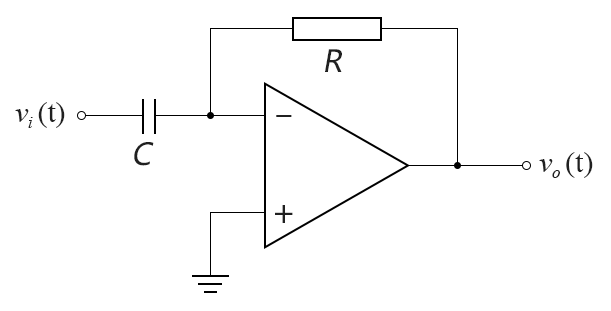
把圖5中電容和電阻的位置交換一下得到如圖8的電路,C1電容充滿電后近似開路,VCC=0V;該電路就是微分運(yùn)算電路的雛形。那么把5V改成信號(hào)源就構(gòu)成了高通濾波電路。
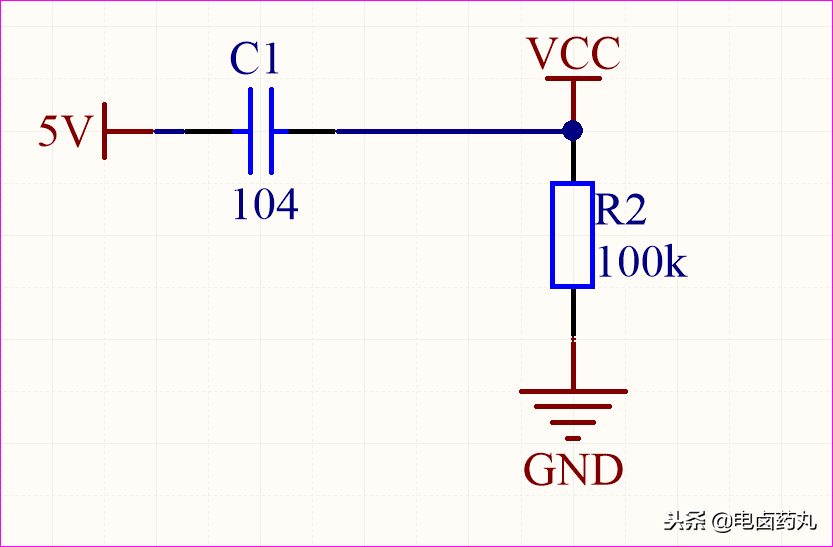
圖8:微分電路
如圖9為上圖的充電波形,紅色表示5V的波形,藍(lán)色表示VCC的波形,因?yàn)殡娙莩潆姇r(shí)的容抗由小變大直至開路,所以分壓VCC由大變小直至為0V。也就是紅色波形從0開始跳變一瞬間,VCC已經(jīng)是最大值,所以微分有超前預(yù)判的性質(zhì)(反映的是輸入信號(hào)的變化率)。
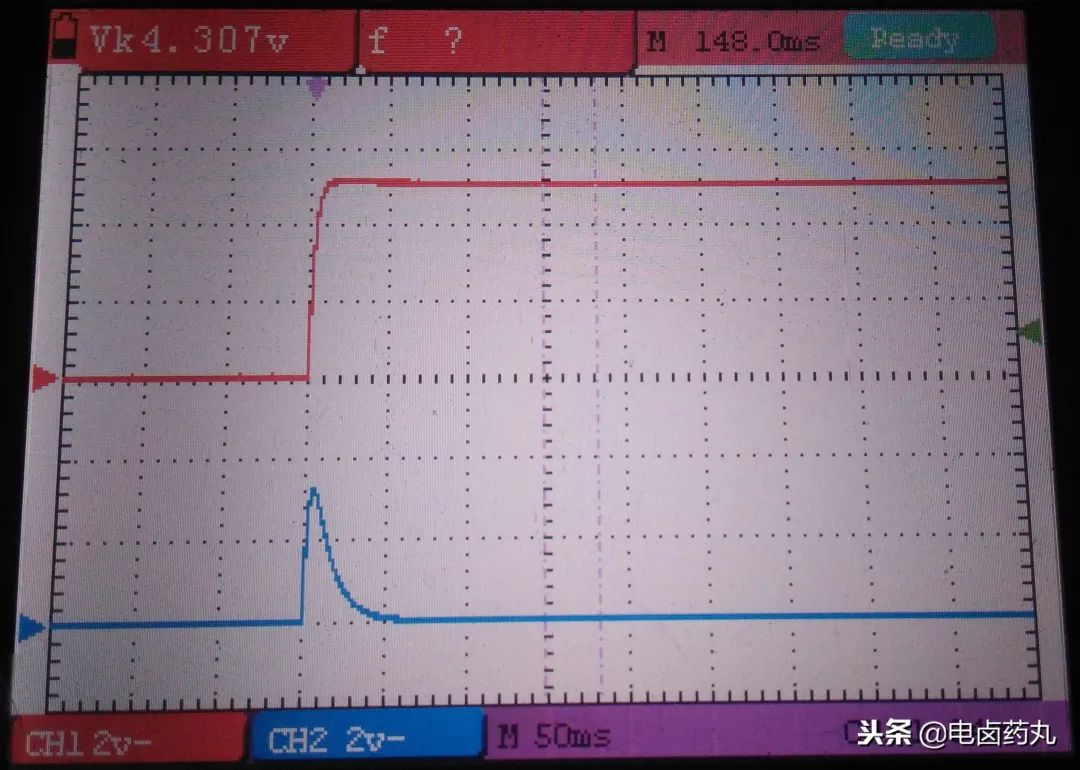
圖9:微分電路波形
如圖10為(反相)比例運(yùn)算電路。
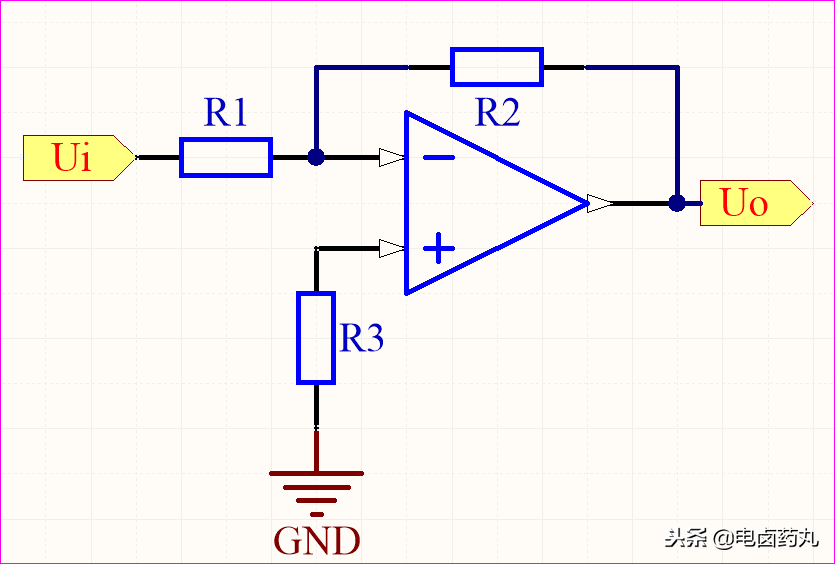
圖10:比例運(yùn)算電路
如圖11,Uo與Ui成線性關(guān)系。
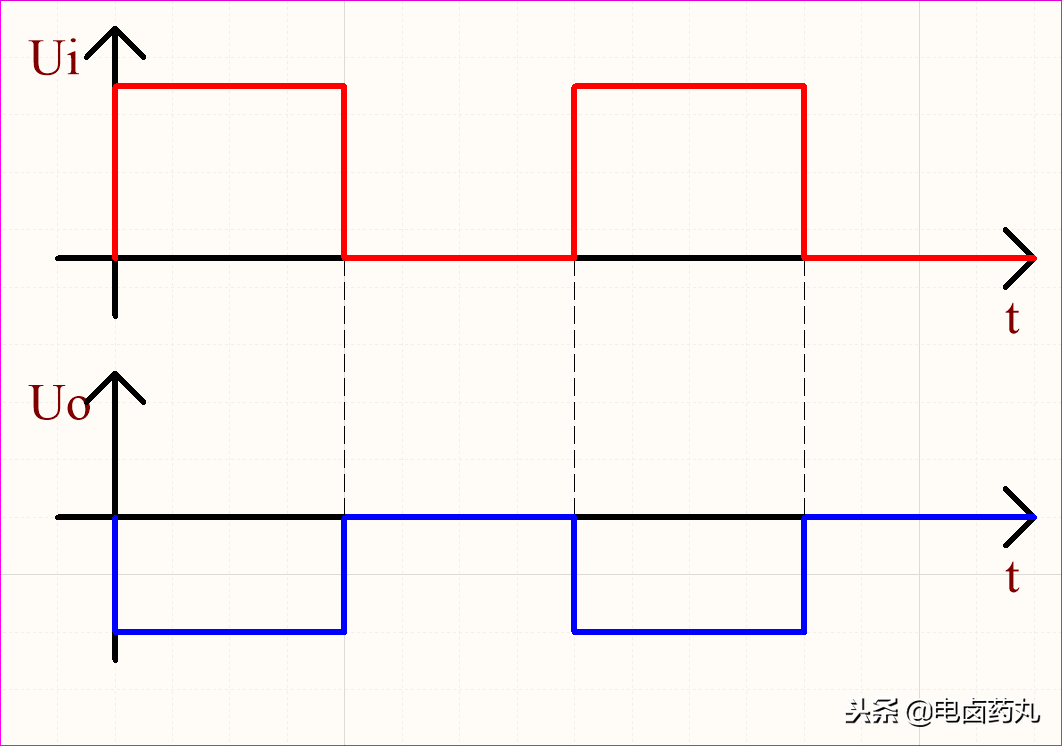
圖11:比例運(yùn)算電路波形
如圖12、圖13為微分運(yùn)算電路的充放電過程:
充電過程的電容C1可等效成一個(gè)可變電阻,C1開始充電時(shí)的容抗為0,電壓不可突變則電壓為0,運(yùn)放-輸入端得到的分壓為正最大峰值,于是Uo為運(yùn)放的負(fù)最大峰值,隨著電容充滿電,U0逐漸變?yōu)?。
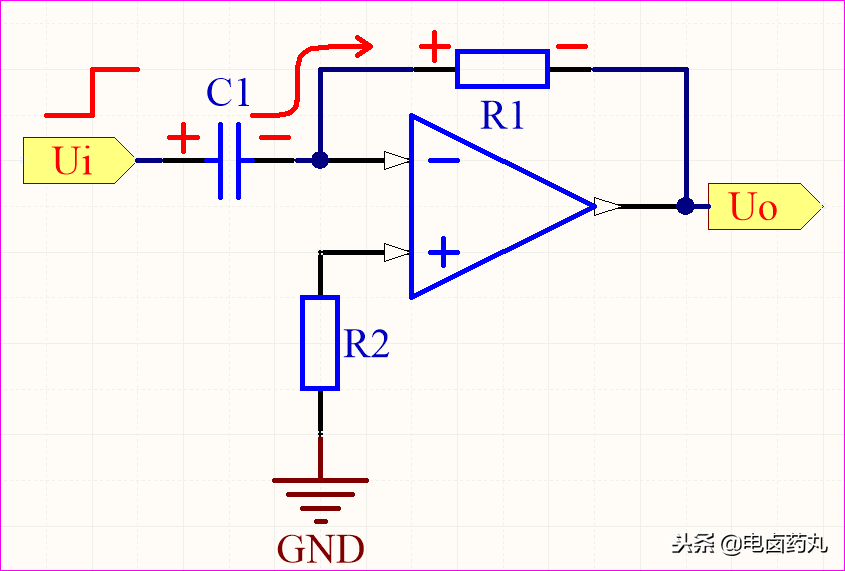
圖12:微分運(yùn)算電路-充電
放電過程的電容C1可等效成一個(gè)電壓源,且電壓不可突變,此時(shí)電流反向?yàn)樽畲笾担琑1電壓瞬間反向也為最大值,運(yùn)放-輸入端得到的分壓則為負(fù)最大峰值,于是Uo為運(yùn)放的正最大峰值,隨著電容放完電,U0逐漸變?yōu)?。
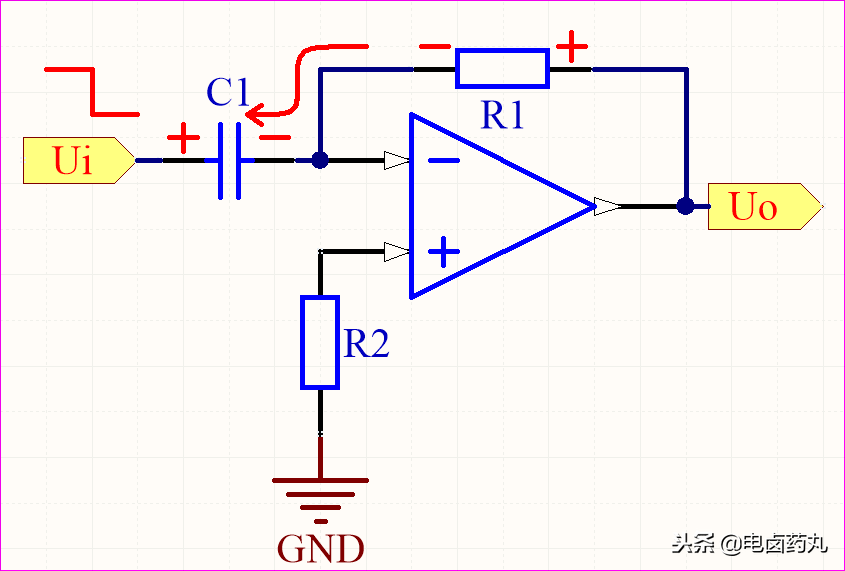
圖13:微分運(yùn)算電路-放電
如圖14為微分運(yùn)算電路的輸入輸出波形,聯(lián)系前面的分析結(jié)果,則Uo反映的是Ui的變化率,這樣就達(dá)到了預(yù)判超前的效果。
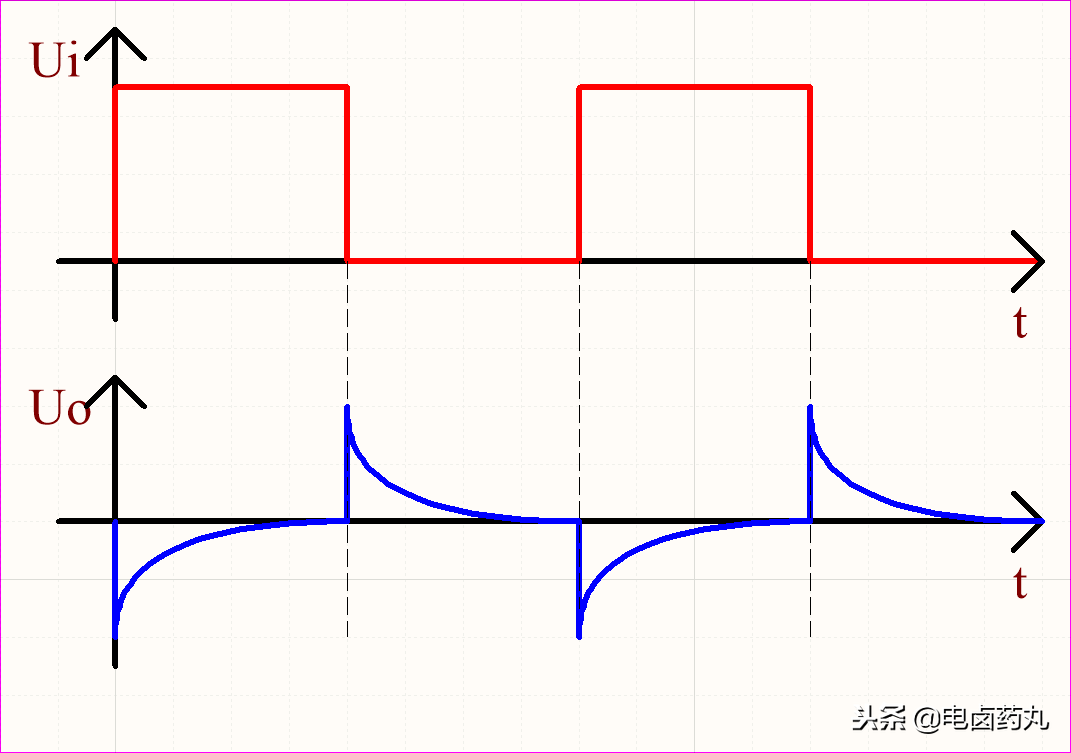
圖14:微分運(yùn)算電路波形
如圖15為微分運(yùn)算仿真電路,為了防止運(yùn)放出現(xiàn)飽和,必須限制輸入電流,實(shí)際使用時(shí)需要在電容C1輸入端串聯(lián)一個(gè)小電阻R2。串聯(lián)電阻后的電路已經(jīng)不是理想微分運(yùn)算電路了,但是只要輸入信號(hào)周期大于2倍RC常數(shù),可以近似為微分運(yùn)算電路。
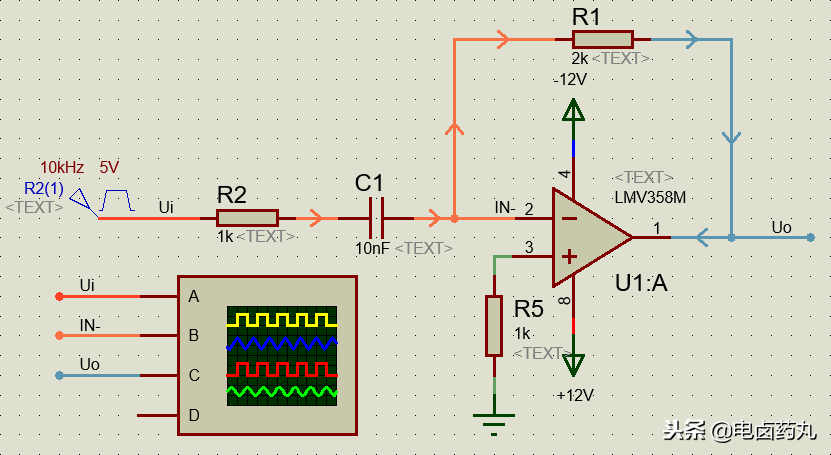
圖15:微分運(yùn)算仿真電路
如圖16為微分運(yùn)算仿真電路波形,其中IN-為運(yùn)放-輸入端的波形。
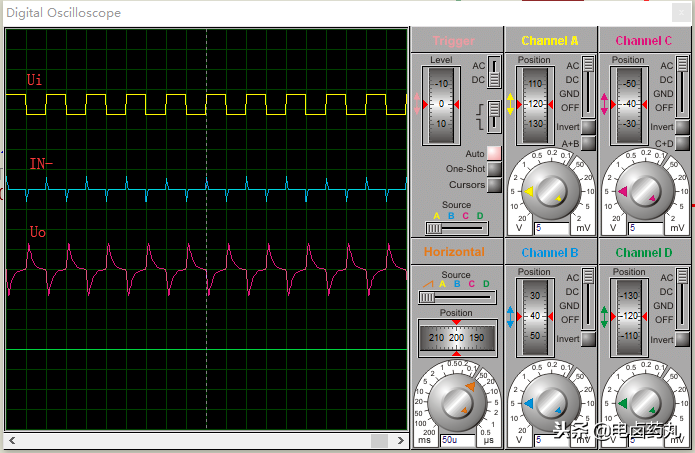
圖16:微分運(yùn)算仿真電路波形
如圖17、圖18為積分運(yùn)算電路的充放電過程:
充電過程的電容C1可等效成一個(gè)可變電阻,C1開始充電時(shí)的容抗為0,電壓不可突變則電壓為0,運(yùn)放-輸入端得到的分壓為0,于是Uo為0,隨著電容充滿電,運(yùn)放-輸入端得到的分壓為正最大值,U0為運(yùn)放的負(fù)最大峰值。
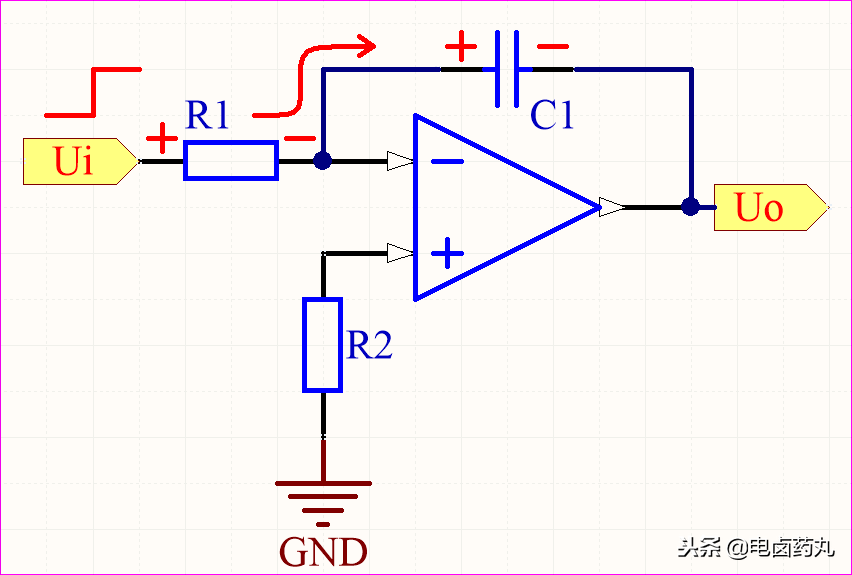
圖15:積分運(yùn)算電路-充電
放電過程的電容C1可等效成一個(gè)電壓源,且電壓不可突變,運(yùn)放-輸入端得到的分壓也不可突變,隨著電容放完電,于是Uo由負(fù)最大峰值逐漸變?yōu)?。
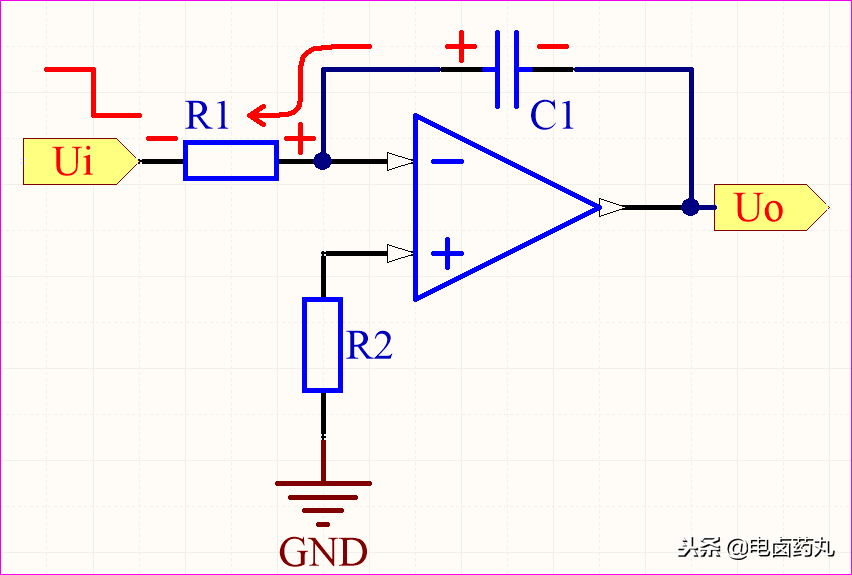
圖16:積分運(yùn)算電路-放電
如圖17為積分運(yùn)算電路的輸入輸出波形,聯(lián)系前面的分析結(jié)果,則Uo反映的是Ui的積累過程,這樣就達(dá)到了延遲穩(wěn)定的效果。
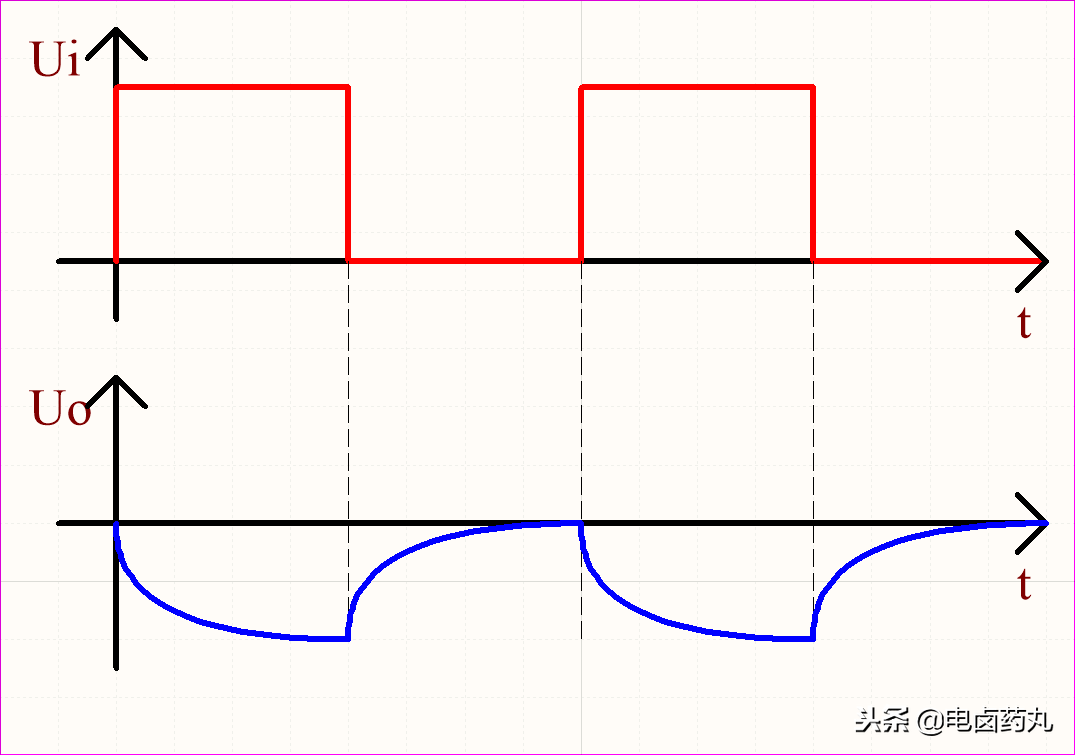
圖17:積分運(yùn)算電路波形
如圖18為積分運(yùn)算仿真電路,為了防止運(yùn)放出現(xiàn)飽和,實(shí)際使用時(shí)需要在電容C2兩端并聯(lián)一個(gè)電阻R3。并聯(lián)電阻后的電路已經(jīng)不是理想積分運(yùn)算電路了,但是只要輸入信號(hào)周期大于2倍RC常數(shù),可以近似為積分運(yùn)算電路。
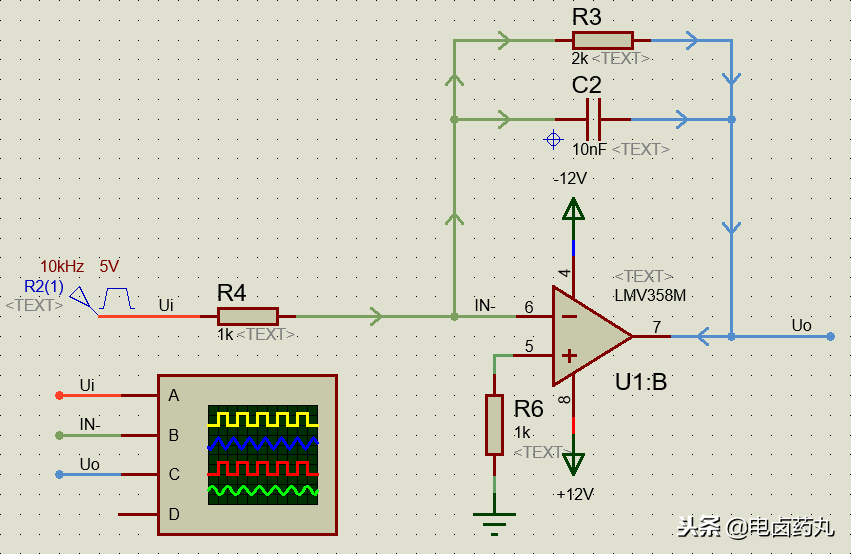
圖18:積分運(yùn)算仿真電路
如圖19為積分運(yùn)算仿真電路波形,其中IN-為運(yùn)放-輸入端的波形。
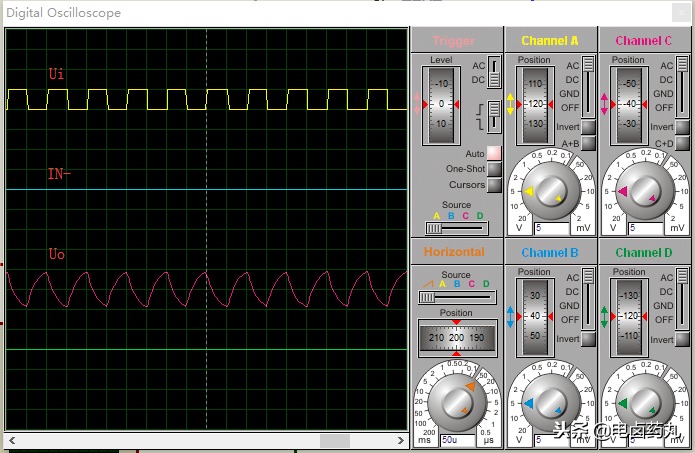
圖19:積分運(yùn)算仿真電路波形
要點(diǎn):
①微分、積分運(yùn)算電路利用了電容充放電時(shí)其電壓不可突變的特性達(dá)到調(diào)節(jié)輸出的目的,對(duì)變化的輸入信號(hào)有意義;
②微分D控制有超前預(yù)判的特性,積分I控制有延遲穩(wěn)定的特性,在PID調(diào)節(jié)速度上,微分D控制>比例P控制>積分I控制。
審核編輯:郭婷
-
電容
+關(guān)注
關(guān)注
100文章
6259瀏覽量
154409 -
PID
+關(guān)注
關(guān)注
37文章
1482瀏覽量
88197 -
積分電路
+關(guān)注
關(guān)注
11文章
86瀏覽量
37479 -
微分電路
+關(guān)注
關(guān)注
4文章
52瀏覽量
20129 -
積分運(yùn)算電路
+關(guān)注
關(guān)注
0文章
5瀏覽量
1949
原文標(biāo)題:學(xué)習(xí)分享|初識(shí)微分、積分電路的本質(zhì)及電容
文章出處:【微信號(hào):Ithingedu,微信公眾號(hào):安芯教育科技】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
RC微分電路與RC積分電路有什么不同
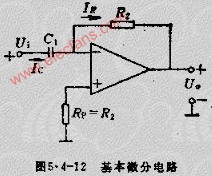
基本微分電路
微分和積分電路的異同
積分電路中電容和電阻的作用
一文徹底掌握微分、積分電路或PID控制思路
關(guān)于微分、積分電路或PID控制思路你都了解嗎
初識(shí)微分、積分電路的本質(zhì)以及電容的陰謀
初識(shí)微分、積分電路的本質(zhì)以及電容的陰謀,不談公式更易懂





















評(píng)論