導數是一種數學工具,用于從任何給定函數獲取變化率。當要微分的函數表示為方程時,我們將應用適當的導數公式以類似的方程格式獲得變化率。當函數為波形時,可以使用稱為微分放大器的電子設備來計算輸入信號的導數。結果是第二個波形,可以記錄、數字化或以其他方式用于提供有關原始波形的其他信息。
在基于計算機的儀器環境中,通過將波形通過軟件中構建的導數函數傳遞波形,可以區分先前記錄到磁盤的波形。后一種方法有幾個優點。與硬件差異化器不同,軟件差異化器是無漂移的,從而提高了精度和可重復性。對生成的差分波形進行自動校準,以輸入波形除以秒為單位。最后,當硬件解決方案生成一個要么接受,要么離開的導數信號時,軟件差異化器允許通過在同一或不同通道上執行多個導數操作來增強靈活性。每個操作都可以有自己的一組參數,為波形分析提供有價值的“假設”方法。
本應用筆記旨在使用DATAQ Instruments的高級CODAS分析包的衍生實用程序作為其模型,探索基于軟件的波形微分的復雜性。本文中討論的波形微分的所有元素都包含在該產品中。
差異化和集成基礎知識
分化和整合之間的關系是如此密切,以至于討論一個自然會導致對另一個的討論。這些強大工具的一個更基本的應用是單位轉換。例如,假設我們正在從汽車獲取以英尺/秒 (ft/sec) 校準的速度波形。利用這個信號,我們可以確定汽車在整個測試過程中任何瞬時點的速度。可以肯定的是,有用的信息。但假設我們對車輛的加速度感到好奇。換句話說,我們想要速度波形相對于時間的變化率。此類信息由導數函數通過將以英尺/秒為單位校準的波形轉換為以英尺/秒/秒或英尺/秒 2 校準的波形來提供。同樣,我們可以選擇對速度波形進行積分,以得出位移的度量。在此操作之后,單位從英尺/秒轉換為(英尺/秒)×秒,或簡稱為“英尺”。
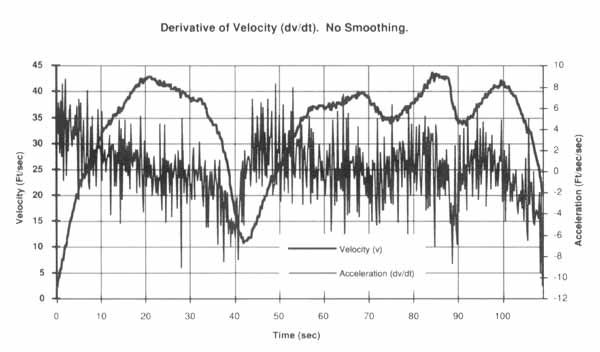
圖 1— 應用導數函數而沒有平滑的好處會產生噪聲結果,幾乎沒有提供有關輸入波形真實變化率的信息。
生成微分波形
再次回到我們的示例速度波形和我們對推導加速度的需求,我們可以確定任何給定范圍內速度的變化,并除以經過的時間以獲得粗略的近似值。但這是一種繁瑣的波形微分方法,很容易導致錯誤,并且無法提供加速度的整體圖形圖像,以幫助我們識別其他感興趣的區域。這些問題可以通過軟件差異化來解決。此類產品可用于導出波形的一階導數的最基本方法是計算速度波形上任何給定點與下一個相鄰樣本之間的差異。然后將此差值除以將兩點分開的經過時間增量,以產生以ft/sec 2或加速度為單位的變化率。這種方法的問題在于結果非常嘈雜,如圖1所示,圖1模擬了這種差異化方法。現實世界的信號總是有一個噪聲分量,隨著微分過程的放大。雖然圖1中的速度波形看起來相當無噪聲,但得出的加速度波形實際上毫無用處。正如模擬微分器提供可選的低通濾波器一樣,軟件微分器也必須提供對生成的波形進行平滑處理的方法。存在許多平滑方法,但最好的方法是將平滑與派生函數相結合,從而提高軟件執行效率。最小二乘算法滿足此要求。
應用于線性回歸的最小二乘法是一種眾所周知的技術,用于推導形式的預測方程。
y = mx + b
來自隨機抽樣的組。從基本微積分中,我們知道這個方程的一階導數(dy/dx)產生m,即直線的斜率或變化率。出于微分目的,截距量 (b) 沒有意義,因此無法計算。有了這些基本信息并將最小二乘線性回歸模型應用于定義采集波形的連續點,我們可以為定義這些點的最佳擬合線構建一個方程,其中線的m或斜率表示線在用于計算的波形值上的平均變化率。進一步擴展此推理,如果我們改變計算回歸線的點數 (n),我們可以調整應用于計算變化率的平滑程度。n值越高,平滑越大,值越低平滑越少。

圖 2— 通過計算由采樣值組成的重疊線段的斜率生成導數波形。
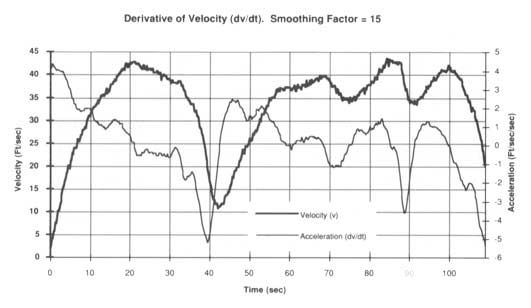
圖 3— 對微分波形進行平滑處理可以顯著提高其可讀性。這里,平滑因子 15 應用于圖 1 所示的相同導數函數。
圖 2以圖形方式演示了如何將回歸模型應用于由y 表示的波形數據點。該示例使用平滑因子 3,這意味著每個線段的斜率 (m) 是通過 3 個連續波形值計算的。請注意線段計算中存在的重疊,它在差分波形中產生的點數與函數y 表示的波形中存在的點數相同。圖3是將回歸方法應用于圖1相同速度波形的結果。計算每條回歸線的點數為 15,從而產生生成的加速度波形中顯示的顯著平滑程度。
圖 4是WinDaq 播放實用程序中打印屏幕的復制品。頂部波形是從在測試軌道上運行的汽車獲得的速度。底部波形是一個計算的通道,加速度,它是通過速度的一階導數得出的,平滑因子為 15。
其他波形差分問題
在選擇分析包來執行波形微分時,應考慮許多問題。首先,確保生成的波形自動縮放為有意義的工程單位。生成的波形應縮放到的單位是原始波形單位除以時間(通常以秒為單位)。這種能力極大地簡化了差異化操作。
其次,波形微分器不應要求數學協處理器來加快計算速度。這樣的要求是惰性編程的副產品,只會給你的系統帶來另一個成本負擔。
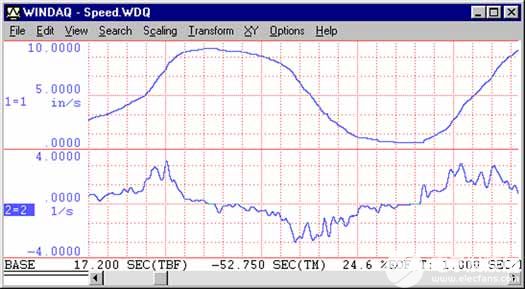
圖 4—WinDaq回放屏幕的再現在頂部窗口中顯示圖 1 和圖 3 的速度波形,在底部窗口中顯示由高級 CODAS 計算的加速度波形。對導數函數應用平滑因子 15。
微分器應使用快速的整數數學運算,而協處理器則沒有優勢。唯一需要的浮點運算是計算縮放常數的單步,該常數將用于在需要時將微分波形縮放為有意義的單位。
最后,檢查分析包的數據空間內存要求。一些分析軟件實用程序要求要操作的波形完全駐留在半導體存儲器中。如果要分析的波形長度僅為10Kb,則沒有問題,但是在嘗試處理2Mb或更大的通道時可能是一個真正的問題。為了使自己免受此類問題的影響,請尋找基于磁盤的分析包。此類系統將要分析的波形從磁盤上流出,通過微分器,并作為計算通道返回磁盤。使用這種方法可以分析的波形信息大小的唯一限制是硬盤驅動器的大小。
審核編輯:郭婷
-
放大器
+關注
關注
145文章
14150瀏覽量
217579 -
電子設備
+關注
關注
2文章
2887瀏覽量
54885 -
計算機
+關注
關注
19文章
7675瀏覽量
90937
發布評論請先 登錄
如何為不同的電機選擇合適的驅動芯片?納芯微帶你深入了解!

深入了解氣密性芯片封裝,揭秘其背后的高科技

深入了解U8g2與LVGL圖形庫
深入了解 PCB 制造技術:銑削
深入了解渦街流量計 原理及內部構造
如何為不同的電機選擇合適的驅動芯片?納芯微帶你深入了解!

【「從算法到電路—數字芯片算法的電路實現」閱讀體驗】+介紹基礎硬件算法模塊
深入了解光伏逆變器測試系統

深入了解基于CANoe的VIO系統應用

深入了解六軸力傳感器:原理、分類與應用
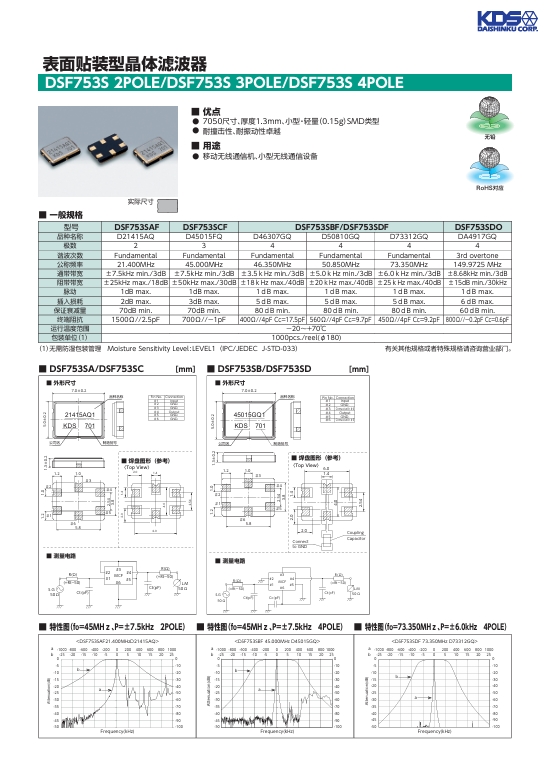
深入了解表面貼裝型晶體濾波器:DSF753S 2POLE、DSF753S 3POLE 和 DSF753S 4POLE
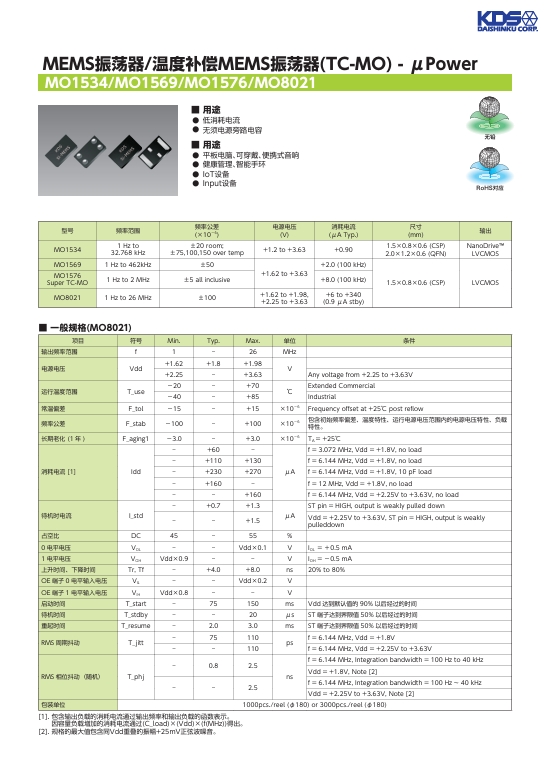
深入了解 MEMS 振蕩器 溫度補償 MEMS 振蕩器 TC-MO





















評論