我們在 深度學習框架(3)-TensorFlow中張量創建和轉化,妙用“稀疏性”提升效率 中討論了如何創建張量并實現張量類型轉化。今天我們一起在TensorFlow中執行張量的計算,并重點討論一下不同的激活函數。
1、了解不同的激活函數,根據應用選擇不同的激活函數
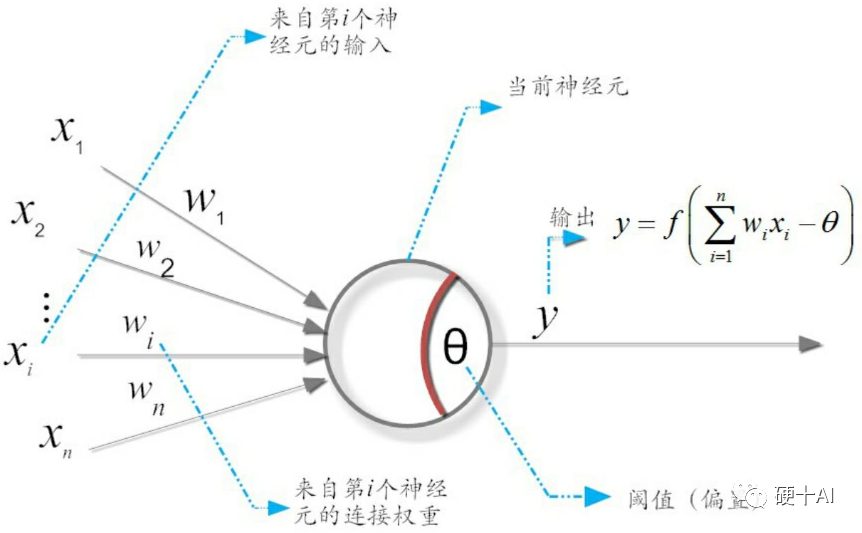
我們在 機器學習中的函數(1)-激活函數和感知機中討論過 激活函數是在神經網絡層間輸入與輸出之間的一種函數變換,目的是為了加入非線性因素,增強模型的表達能力。激活函數的作用類似于人類大腦中基于神經元的模型(參考下圖),激活函數最終決定了要發射給下一個神經元的內容。
(1)激活函數有什么價值?
激活函數對于人工神經網絡模型去學習、理解非常復雜和非線性的函數來說具有十分重要的作用。首先對于y=ax+b這樣的函數,當x的輸入很大時,y的輸出也是無限大/小的,經過多層網絡疊加后,值更加膨脹了,這顯然不符合我們的預期,很多情況下我們希望的輸出是一個概率,需要激活函數能幫助網絡進行收斂。其次,線性變換模式相對簡單(只是加權偏移),限制了對復雜任務的處理能力,沒有激活函數的神經網絡就是一個線性回歸模型;激活函數做的非線性變換可以使得神經網絡處理非常復雜的任務,如我們希望我們的神經網絡可以對語言翻譯和圖像分類做操作,這就需要非線性轉換。最后,激活函數也使得反向傳播算法變得可能,因為這時候梯度和誤差會被同時用來更新權重和偏移,沒有可微分的線性函數,就不可能實現。
(2)有哪些常用的激活函數?
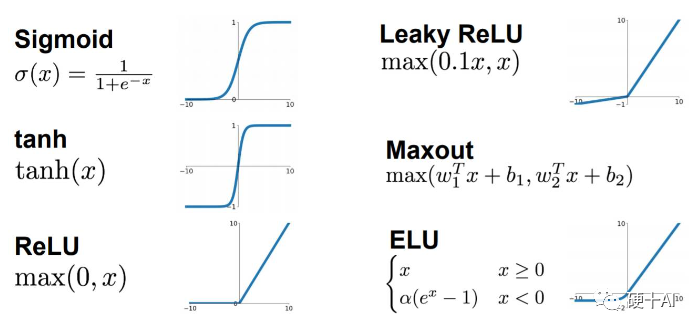
常用的激活函數有,Sigmoid激活函數,Tan/ 雙曲正切激活函數,ReLU激活函數(還有改進后的LeakyReLU和PReLU),Softmax激活函數等。
(3)激活函數使用時有哪些問題?如何改進激活函數?
Sigmoid梯度消失問題可以通過Relu解決
梯度、梯度下降、鏈式法則等概念可參考機器學習中的函數(3)-“梯度下降”走捷徑,“BP算法”提效率 中的描述。我們以Sigmoid為例,看一下“梯度消失”是如何發生的?Sigmoid的函數公式和圖像如下圖,從圖中可見函數兩個邊緣的梯度約為0,Sigmoid導數取值取值范圍為(0,0.25)。
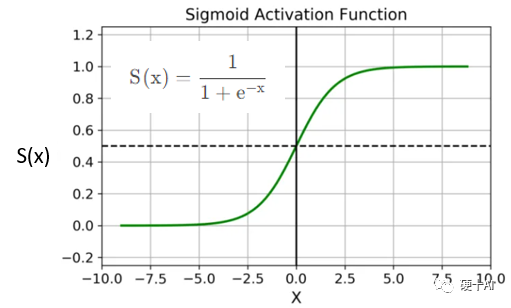
當我們求激活函數輸出相對于權重參數W的偏導時,Sigmoid函數的梯度是表達式中的一個乘法因子。實際的神經網絡層數少則數十多則數百層,由于神經網絡反向傳播時的“鏈式反應”,這么多范圍在(0,0.25)的數相乘,將會是一個非常小的數字。而梯度下降算法更新參數W完全依賴于梯度值(如BP算法),極小的梯度值失去了區分度,無法讓參數有效更新,該現象即為“梯度消失”(VanishingGradients)。
ReLU激活函數(Rectified Linear Unit,修正線性單元)的出現解決了梯度消失問題。如下圖所示,ReLU的公式是R(z)=max(0,z)。假設這個神經元負責檢測一個具體的特征,例如曲線或者邊緣。若此神經元在輸入范圍內檢測到了對應的特征,開關開啟,且正值越大代表特征越明顯;但此神經元檢測到特征缺失,開關關閉,則不管負值的大小,如-6對比-2都沒有區分的意義。
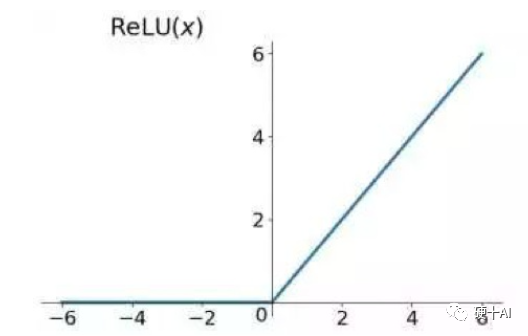
Relu的優勢是求導后,梯度只可以取0或1,輸入小于0時,梯度為0;輸入大于0時,梯度為1。在多層神經網絡中Relu梯度的連續乘法不會收斂到0,結果也只可以取0或1;若值為1則梯度保持值不變進行前向傳播,若值為0則梯度從該位置停止前向傳播。
Relu神經元死亡問題可以通過“小于0”部分優
ReLU也有缺點,它提升了計算效率,但同樣可能阻礙訓練過程。通常,激活函數的輸入值有一項偏置項(bias),若bias太小,輸入激活函數的值總是負的,那么反向傳播過程經過該處的梯度總為0,對應的權重和偏置參數無法得到更新。如果對于所有的樣本輸入,該激活函數的輸入都是負的,那么該神經元再也無法學習,稱為神經元“死亡”問題(Dying ReLU Problem)。
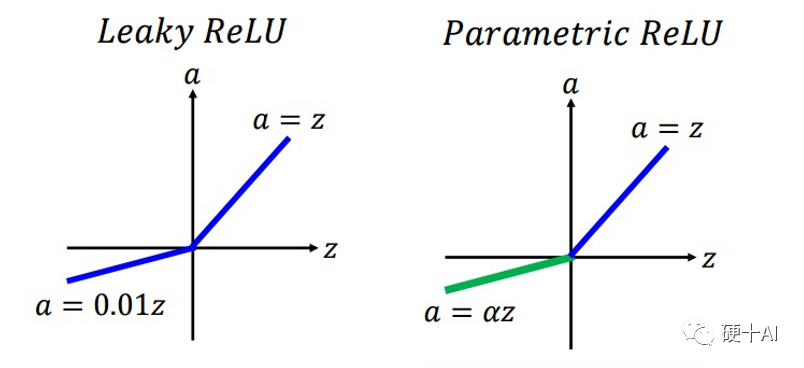
Relu升級到LeakyReLU就是為了解決神經元“死亡”問題。LeakyReLU與ReLU很相似,僅在輸入小于0的部分有差別,ReLU輸入小于0的部分值都為0,而LeakyReLU輸入小于0的部分,值為負,且有微小的梯度。使用LeakyReLU的好處就是:在反向傳播過程中,對于LeakyReLU激活函數輸入小于零的部分,也可以計算得到梯度,而不是像ReLU一樣值為0,這樣就避免了上述梯度方向鋸齒問題。超參數α的取值也被研究過,有論文將α作為了需要學習的參數,該激活函數為PReLU(Parametrized ReLU)。
(4)如何選擇激活函數?
每個激活函數都有自己的特點,Sigmoid和tanh的將輸出限制在(0,1)和(-1,1)之間,適合做概率值的處理,例如LSTM中的各種門;而ReLU無最大值限制,則不適合做這個應用,但是Relu適合用于深層網絡的訓練,而Sigmoid和tanh則不行,因為它們會出現梯度消失。
選擇激活函數是有技巧的,如“除非在二分類問題中,否則小心使用Sigmoid函數”;“如果你不知道應該使用哪個激活函數, 那么請優先選擇ReLU”。盡管ReLU有一些缺點,但參考“奧卡姆剃刀原理”,如無必要、勿增實體,也就是優先選擇最簡單的方法,ReLU相較于其他激活函數,有著最低的計算代價和最簡單的代碼實現。如果使用了ReLU,要注意一下DeadReLU問題。如優化Learningrate,防止太高導致在訓練過程中參數更新太大,避免出現大的梯度從而導致過多的神經元“Dead”;或者針對輸入為負值時,ReLU的梯度為0造成神經元死亡,更換激活函數,嘗試一下leakyReLU等ReLU變體,說不定會有很好效果。
實際應用時還是要看具體場景,甚至結合具體模型。比如LSTM中用到Tanh、Transfromer中用到的ReLU、Bert中用到的GeLU,YoLo中用到的LeakyReLU等。不同的激活函數,根據其特點,應用各不相同。
3、如何讓張量執行計算?
(1)導入TensorFlow,并建立矩陣a、矩陣b、矩陣c,參考如下代碼
import tensorflow as tf
import numpy as np
a = tf.constant([[1, 2], [3, 4]])
b = tf.constant([[1, 1], [1, 1]])
c = tf.constant([[4.0,5.0], [10.0,1.0]])
(2)執行張量的運算
張量的基本運算包括加法、乘法、獲取最大最小值等,常用函數有tf.add()、tf.multiply()、tf.matmul()、tf.reduce_max()等。乘法相關的兩個函數,tf.multiply()是兩個矩陣中對應元素各自相乘,而tf.matmul()執行的是矩陣乘法,兩者有區別。
add
print(tf.add(a, b), “
”)
打印結果 》》》
tf.Tensor(
[[2 3]
[4 5]], shape=(2, 2), dtype=int32)
multiply
print(tf.multiply(a, b), “
”)
打印結果 》》》
tf.Tensor(
[[1 2]
[3 4]], shape=(2, 2), dtype=int32)
matrix multiply
print(tf.matmul(a, b), “
”)
打印結果 》》》
tf.Tensor(
[[3 3]
[7 7]], shape=(2, 2), dtype=int32)
max/min:find the largest/smallest value
print(tf.reduce_max(c))
打印結果 》》》
tf.Tensor(10.0, shape=(), dtype=float32)
(3)應用激活函數
我們以tf.nn.sigmoid()、tf.nn.relu()等常用的激活函數為例,大家可以參考上文分享的公式驗計算驗證一下,看一下激活效果。
sigmoidprint(tf.nn.sigmoid(c))
打印結果 》》》
tf.Tensor(
[[0.98201376 0.9933072 ]
[0.9999546 0.7310586 ]], shape=(2, 2), dtype=float32)
reluprint(tf.nn.relu(c))
打印結果 》》》
tf.Tensor(
[[ 4. 5.]
[10. 1.]], shape=(2, 2), dtype=float32)
今天我們一起學習了如何在TensorFlow中執行張量的計算,并重點討論一下不同的激活函數,下一步我們繼續學習如何使用TensorFlow
審核編輯:郭婷
-
神經網絡
+關注
關注
42文章
4779瀏覽量
101032 -
深度學習
+關注
關注
73文章
5512瀏覽量
121404
原文標題:深度學習框架(4)-TensorFlow中執行計算,不同激活函數各有妙用
文章出處:【微信號:Hardware_10W,微信公眾號:硬件十萬個為什么】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
半導體所在光學張量處理領域取得新進展
自動化創建UI并解析數據
RK3568國產處理器 + TensorFlow框架的張量創建實驗案例分享
自動化創建UI并解析數據
《算力芯片 高性能 CPUGPUNPU 微架構分析》第3篇閱讀心得:GPU革命:從圖形引擎到AI加速器的蛻變
輸入文字轉化語音
Groq籌資約3億美元,向Cerebras等對手看齊?
FPGA設計中 Verilog HDL實現基本的圖像濾波處理仿真
深度解析Transformer技術原理

將yolov5s的模型轉成.onnx模型,進行cube-ai分析時報錯的原因?
arcgis值類型與字段類型不兼容
應用大模型提升研發效率的實踐與探索





 如何創建張量并實現張量類型轉化
如何創建張量并實現張量類型轉化










評論