了解如何將抖動添加到信號以通過消除量化誤差和失真來提高模數轉換系統的性能。
有時,電子噪音可能是因禍得福。在本文中,我們將了解“抖動”,它指的是一種將適當的噪聲成分添加到信號中以提高A/D(模數)轉換系統性能的技術。
什么是抖動?
大多數 EE 都熟悉限制電子電路中噪聲水平的方法。過濾是一種常用技術,可用于消除噪聲成分或至少限制其帶寬。在某些應用中,例如降噪耳機和降噪低噪聲放大器 (LNA),我們甚至可以測量主要噪聲分量并將其從系統輸出中減去以實現所需的性能。
盡管有這些應用,但在模數轉換系統中我們需要噪聲來提高電路性能。這種信號處理技術,稱為抖動,故意將具有適當 PDF(概率密度函數)和 PSD(功率譜密度)的噪聲信號添加到 ADC(模數轉換器)輸入(采樣和量化之前),以改善某些系統的性能方面。圖 1 顯示了抖動系統的簡化框圖(該圖表示一種稱為非減色抖動的抖動)。
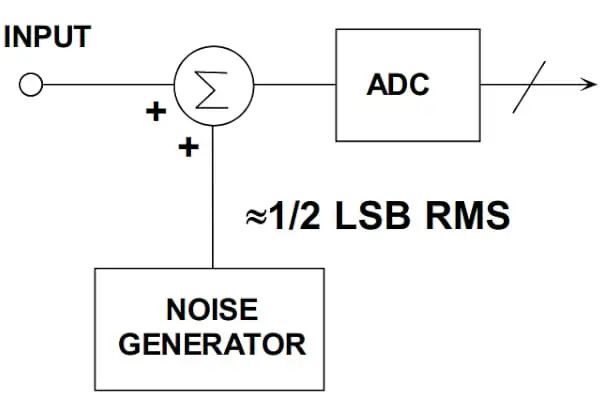
圖 1.顯示抖動系統框圖的示例圖。圖片由Analog Devices提供
第一次了解抖動時,可能會發現某種程度的噪聲在某些情況下實際上是有幫助的,這違反直覺。抖動技術可用于三個不同的目的:
通過打破量化誤差和輸入信號之間的統計相關性來提高理想量化器的性能
隨機化非理想 ADC 上的DNL(微分非線性)誤差模式以提高無雜散動態范圍 (SFDR) 性能
通過對緩慢變化的信號進行平均來提高測量分辨率
在本文中,我們將討論抖動如何通過打破量化誤差與輸入信號之間的統計相關性來改進理想的量化器,但在此之前,我們需要了解一下 ADC 量化噪聲。
ADC 量化誤差的高級基礎知識
ADC 表示通過多個離散級別的連續范圍的模擬值,這固有地增加了稱為量化誤差的誤差。已進行大量研究以充分理解此錯誤。研究歷史實際上可以追溯到 1948 年 WR Bennett 的一篇論文“量化信號的頻譜”。今天,眾所周知,在某些條件下,量化誤差可以建模為一種加性噪聲,在兩者之間均勻分布±大號小號乙2個LSB2(LSB 表示轉換器的最低有效位)。
此外,假定量化噪聲為白噪聲(即,在直流到 fs/2 的奈奎斯特帶寬上均勻分布),總功率等于大號小號乙2個12.平坦頻譜特性基于量化誤差樣本彼此不相關的假設。
在本文中,我們將這種量化誤差模型稱為“量化噪聲模型”。我們將很快討論量化噪聲模型并不總是有效;然而,對于許多實際應用來說,它仍然足夠準確。下面的例子說明了為什么處理數據轉換器的 EE 喜歡這個模型!
10 位與 12 位 ADC:多少位就足夠了?
讓我們考慮一個應用,其中 ADC 的參考電壓為 2 V。假設 ADC 輸入信號的噪聲為 1 mV RMS(均方根)。對于 10 位 ADC,LSB 是2個2個10= 1.95 mV,因此,噪聲的 RMS 值等于 0.51 LSB。
從量化噪聲模型中,我們知道量化操作添加了 RMS 噪聲大號小號乙12= 0.29 最低有效位。
如您所見,量化噪聲與來自輸入的原始噪聲相當。要找到系統的總噪聲功率,我們應該將兩個噪聲源的功率相加:
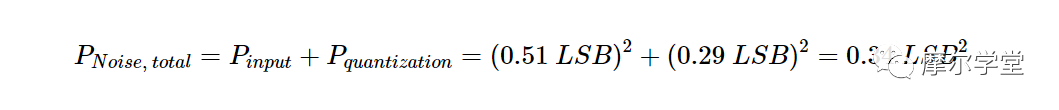
對該值求平方根,得出總噪聲的 RMS 為 0.59 LSB。如果我們的應用不能接受此噪聲水平,我們可以提高 ADC 分辨率以降低量化噪聲。例如,對于 12 位 ADC,輸入噪聲為 2.05 LSB RMS。與輸入噪聲相比,量化噪聲 (0.29 LSB) 現在幾乎可以忽略不計。對于這個例子,總噪聲 RMS 達到 2.07 LSB。12 位系統似乎可以為該應用程序提供足夠的分辨率。
有了信號中的總噪聲,我們就可以確定交流應用中的信噪比 (SNR) 或測量應用中的最小可檢測信號。這里的重點是噪聲模型使我們能夠輕松地考慮量化過程對系統噪聲性能的影響。
作為旁注,值得一提的是,上述討論隱含地假設 ADC 添加的主要噪聲是量化噪聲。這并非總是如此。隨著我們提高 ADC 分辨率,量化噪聲變得越來越小。在某些時候,與 ADC 內由 ADC 內部電路的熱噪聲和閃爍噪聲產生的電子噪聲相比,量化噪聲可以忽略不計。今天的高分辨率ΔΣ (delta-sigma) ADC就是這種情況。如果量化噪聲可以忽略不計,則應考慮ADC的峰峰值輸入參考噪聲來分析系統噪聲性能。
量化誤差的頻率成分
量化噪聲模型的一個含義是誤差與輸入不相關。為了更好地理解這一點,請考慮圖 2 中的波形。
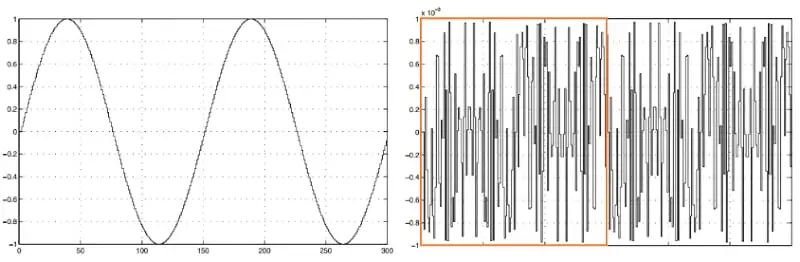
圖 2.示例波形。圖片由Franco Maloberti提供
上圖中的左側曲線描繪了 10 位量化正弦波的兩個周期。右曲線顯示量化誤差。本例中,采樣頻率與輸入頻率之比為150。通過目測可以確認量化誤差是周期性的(一個周期用橙色矩形表示)。此外,輸入和量化誤差信號之間存在相關性。由此,我們知道周期信號的頻率成分集中在信號基頻的倍數處。這意味著雖然量化噪聲模型期望誤差具有平坦的頻譜,但量化誤差具有一些強頻率分量。
這是一個普遍問題:如果輸入是正弦波并且采樣頻率是輸入頻率的倍數,則量化誤差與輸入信號相關。另一個示例如圖 3 所示。
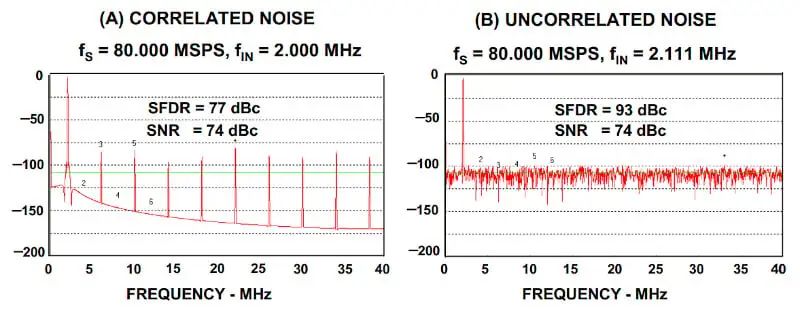
圖 3.顯示相關噪聲 (a) 和不相關噪聲 (b) 的示例圖。圖片由Analog Devices提供
左側曲線顯示了輸入為 2 MHz 正弦波且采樣頻率為 80 MSPS 時理想 12 位 ADC 的頻譜。右側曲線顯示同一 ADC 的頻譜,該 ADC 以相同采樣頻率采樣 2.111 MHz 正弦波。正如所料,當采樣頻率與輸入頻率之比為整數時,輸出端會產生輸入頻率的不同諧波。對于左側曲線,系統的無寄生動態范圍 (SFDR)僅為 77 dBc。通過稍微改變輸入頻率,諧波分量消失,我們得到一個草地般的本底噪聲。
請注意,兩種情況下量化誤差的 RMS 值相同,導致 SNR 為 74 dBc(12 位 ADC 可獲得的理論值)。對于這兩種情況,RMS 誤差都與量化噪聲模型預測的值一致(大號小號乙12);然而,誤差的頻譜在左圖中并不平坦。
上述諧波分量是量化過程的產物,與 ADC 電路的性能無關。這突出了有關 ADC 測試的一個重要警告:如果輸入信號是采樣頻率的精確約數,我們為單音正弦波快速傅里葉變換 (FFT)測試獲得的頻譜將受到量化過程偽影的影響。
總而言之,如果量化誤差與輸入相關,我們不能假設 ADC 只會增加輸入的本底噪聲。在這種情況下,量化噪聲模型不再有效,量化過程會在輸出頻譜中產生顯著的諧波分量。通常,我們更希望誤差能量散布在較寬的頻帶上,而不是集中在某些特定頻率上。
量化低幅度信號
量化低幅度信號也會導致量化誤差與輸入之間的相關性。低幅度信號可能成為問題的一個示例應用是數字音頻系統。假設 ADC 輸入的幅度下降到 0.75 LSB,如圖 4 所示。
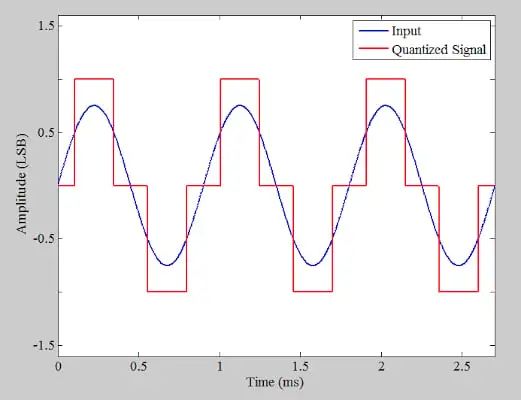
圖 4.顯示 ADC 輸入下降幅度的示例圖。
如您所見,量化信號僅采用三個不同的值,并且具有類似方波的形狀。我們知道方波的頻譜包含基頻的不同諧波。在上面的例子中,輸入是 1.11 kHz 的正弦波,采樣頻率是 400 kHz(特意選擇遠高于奈奎斯特采樣定理所要求的頻率)。輸出的 FFT 如圖 5 所示。
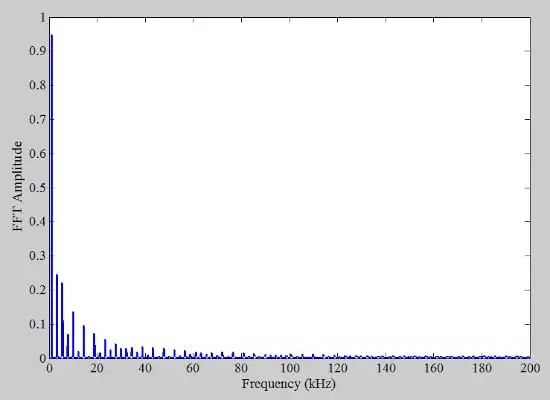
圖 5.顯示 FFT 振幅與頻率的關系圖。
盡管輸入頻率 (1.11 kHz) 不是采樣頻率 (400 kHz) 的約數,但頻譜包含大量諧波分量。這些諧波在圖 6 提供的放大版頻譜中更容易辨別。
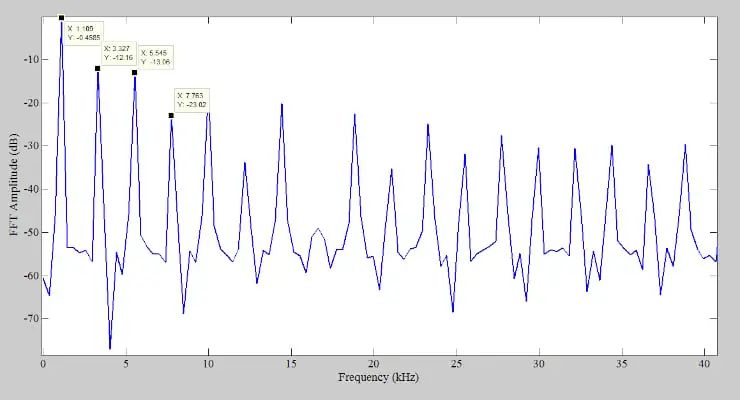
圖 6.頻譜的放大版本。
抖動的優點
為了檢查抖動技術,我們將具有三角形分布的噪聲添加到上述信號中,然后對其進行量化。三角抖動 pdf(概率密度函數)的寬度取為 2 LSB。波形如圖 7 所示。

圖 7.添加具有三角分布的噪聲并進行量化后的示例波形。
在時域,好像信息丟失了,但是頻域呢?新量化信號的頻譜(上圖紅色曲線)如圖 8 所示。
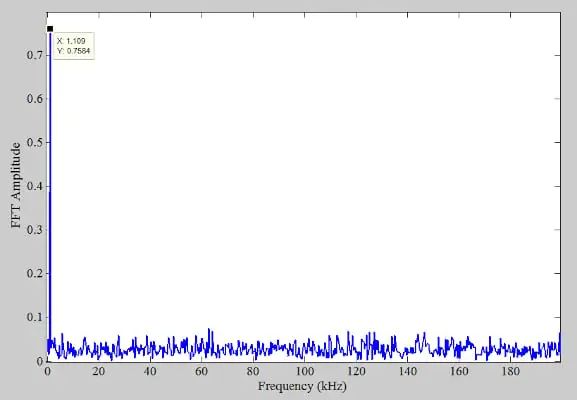
圖 8.新量化信號的頻譜。
抖動消除了諧波分量。事實上,諧波分量的能量分布在很寬的頻帶上。因此,當我們應用抖動技術時,我們預計本底噪聲會略有上升。除了這種影響之外,添加到輸入端的抖動噪聲也會導致本底噪聲增加。
上面的例子清楚地顯示了抖動在頻譜分析應用中的優勢。然而,有趣的是,即使不將信號轉換到頻域,我們也可以從抖動中獲益。例如,在數字音頻中,無特征背景噪聲的增加(由于抖動)在感知上比量化器引入的人工諧波更容易接受。
從抖動噪聲中獲益
量化噪聲模型的一個含義是量化誤差與輸入不相關。如果不是這種情況,則量化操作會引入一種失真,有時稱為“量化失真”。通過添加抖動噪聲,消除了量化誤差與輸入之間的相關性。這因此消除了由量化操作產生的諧波分量。這樣,抖動可以提高理想量化器的性能。如上所述,抖動還用于其他幾個目的。在本系列的下一篇文章中,我們將進一步深入討論。
最后一點,值得一提的是,在大多數系統中,輸入信號具有足夠的噪聲,因此不需要添加額外的抖動噪聲來打破量化噪聲與輸入之間的相關性。此外,ADC 的輸入參考噪聲可能足以產生相同的抖動效果。
審核編輯 :李倩
-
adc
+關注
關注
98文章
6507瀏覽量
544910 -
模數轉換
+關注
關注
1文章
216瀏覽量
36885 -
檢測信號
+關注
關注
0文章
6瀏覽量
6314
原文標題:什么是抖動?使用抖動消除量化失真
文章出處:【微信號:moorexuetang,微信公眾號:摩爾學堂】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
抖動定義和測量

LMH6642原始信號加載在一條斜線上,基線抖動厲害,如何消除這種抖動或者減小它?
CDR電路設計與抖動管理
抖動的概念和類型 量化時域抖動、隨機抖動和頻域抖動的方法
FPGA如何消除時鐘抖動
了解并盡量減少抖動對高速鏈路的影響




 什么是抖動?使用抖動消除量化失真
什么是抖動?使用抖動消除量化失真











評論